【沪科版九年级数学上册课时作业】21.5.3 反比例函数的应用(含答案)
文档属性
| 名称 | 【沪科版九年级数学上册课时作业】21.5.3 反比例函数的应用(含答案) | 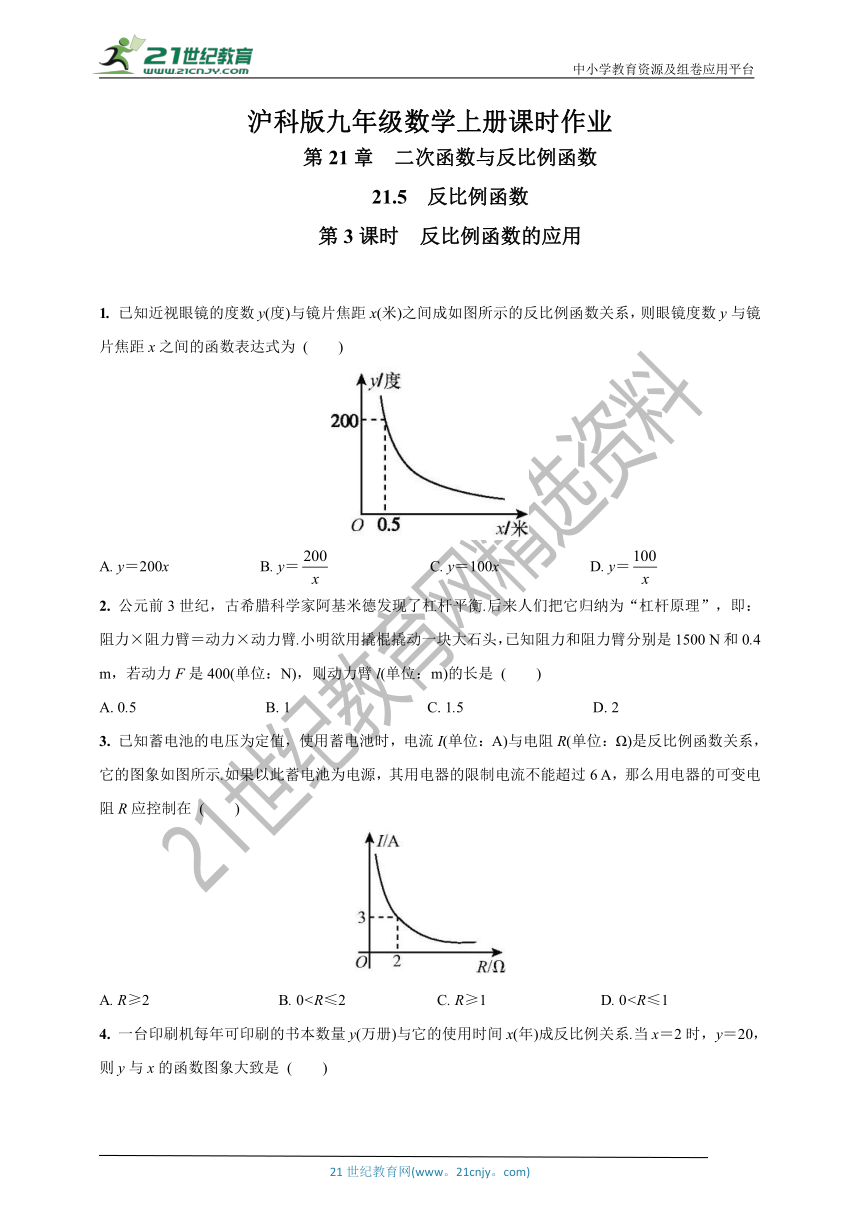 | |
| 格式 | doc | ||
| 文件大小 | 324.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 16:08:51 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
沪科版九年级数学上册课时作业
第21章 二次函数与反比例函数
21.5 反比例函数
第3课时 反比例函数的应用
1. 已知近视眼镜的度数y(度)与镜片焦距x(米)之间成如图所示的反比例函数关系,则眼镜度数y与镜片焦距x之间的函数表达式为 ( )
A. y=200x B. y= C. y=100x D. y=
2. 公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡.后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小明欲用撬棍撬动一块大石头,已知阻力和阻力臂分别是1500 N和0.4 m,若动力F是400(单位:N),则动力臂l(单位:m)的长是 ( )
A. 0.5 B. 1 C. 1.5 D. 2
3. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.如果以此蓄电池为电源,其用电器的限制电流不能超过6 A,那么用电器的可变电阻R应控制在 ( )
A. R≥2 B. 04. 一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系.当x=2时,y=20,则y与x的函数图象大致是 ( )
A B C D
5. 为了建设生态文明,某工厂自2021年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分.下列选项错误的是 ( )
A. 4月份的利润为50万元
B. 治污改造完成后每月利润比前一个月增加30万元
C. 治污改造完成前后共有4个月的利润低于100万元
D. 9月份该厂利润达到200万元
6. 学校锅炉旁建有一个储煤库,开学初购进一批煤,现在知道:按每天用煤0.6吨计算,一学期(按150天计算)刚好用完.若每天的耗煤量为0.5吨,那么这批煤能维持 天.?
7. 在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,p=50,则当p=25时,V= .?
8. 电压一定时,电流与电阻成反比,I=的图象过点(1,36),当I=18 A,则R的值为 Ω.?
9. 在照明系统模拟控制电路实验中,研究人员发现光敏电阻值R(单位:Ω)与光照度E(单位:lx)之间成反比例函数关系,部分数据如下表所示:
光照度E/lx 0.5 1 1.5 2 2.5 3
光敏电阻值R/Ω 60 30 20 15 12 10
则光敏电阻值R与光照度E的函数表达式为 .?
10. 随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当x≥10时,y与x成反比例函数关系,当车速低于20千米/时时,交通就会拥堵.为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是 .?
11. 秋季是传染病的高发季节.为预防传染病,某学校会定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10 min燃烧完,此时教室内每立方米空气中的含药量为6 mg.研究表明当每立方米空气中的含药量不低于1.2 mg时,消毒才有效,则这次有效的消毒时间是 min.?
12. 湖州市菱湖镇某养鱼专业户准备挖一个面积为2000平方米的长方形鱼塘.
(1)求鱼塘的长y(米)关于宽x(米)的函数表达式;
(2)由于受场地的限制,鱼塘的宽最多只能挖20米,当鱼塘的宽是20米时,鱼塘的长为多少米?
13. 在对某物体做功一定的情况下,力F(N)与物体在力的方向上移动的距离s(m)成反比例函数关系,且当s=10 m时,F=3 N.
(1)试确定F(N)与s(m)之间的函数表达式;
(2)求当力F=15 N时,物体在力的方向上移动的距离s.
14. 已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时).
(1)求v关于t的函数表达式;
(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?
15. 某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB,BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10 ℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?
参 考 答 案
1. D 2. C 3. C 4. C 5. C
6. 180
7. 400
8. 2
9. R=
10. 011. 48
12. 解:(1)由长方形面积为2000平方米,得到xy=2000,即y=.
(2)当x=20时,y==100,则当鱼塘的宽是20米时,鱼塘的长为100米.
13. 解:(1)设F=,由当s=10时,F=3,得3=,k=30,∴F与s之间的函数表达式是F=.
(2)当力F=15时,15=,s=2,即物体在力的方向上移动的距离为2 m.
14. 解:(1)由题意可得100=vt,∴v=.
(2)∵不超过5小时卸完船上的这批货物,∴t≤5,∴v≥=20. 答:平均每小时至少要卸货20吨.
15. 解:(1)设线段AB的函数表达式为y=k1x+b(k≠0),∵线段AB过点(0,10),(2,14),代入得 解得 ∴线段AB的函数表达式为y=2x+10(0≤x<5). ∵点B在线段AB上,当x=5时,y=20,∴点B的坐标为(5,20),∴线段BC的函数表达式为y=20(5≤x<10). 设双曲线CD的函数表达式为y=(k2≠0),∵点C的坐标为(10,20),∴k2=200,∴双曲线CD的函数表达式为y=(10≤x≤24),∴y关于x的函数表达式为y=
(2)由(1)得恒温系统设定的恒定温度为20 ℃.
(3)把y=10代入y=中,解得x=20,∴20-10=10. 答:恒温系统最多可以关闭10小时.
_21?????????è?????(www???21cnjy???com)_
沪科版九年级数学上册课时作业
第21章 二次函数与反比例函数
21.5 反比例函数
第3课时 反比例函数的应用
1. 已知近视眼镜的度数y(度)与镜片焦距x(米)之间成如图所示的反比例函数关系,则眼镜度数y与镜片焦距x之间的函数表达式为 ( )
A. y=200x B. y= C. y=100x D. y=
2. 公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡.后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小明欲用撬棍撬动一块大石头,已知阻力和阻力臂分别是1500 N和0.4 m,若动力F是400(单位:N),则动力臂l(单位:m)的长是 ( )
A. 0.5 B. 1 C. 1.5 D. 2
3. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.如果以此蓄电池为电源,其用电器的限制电流不能超过6 A,那么用电器的可变电阻R应控制在 ( )
A. R≥2 B. 0
A B C D
5. 为了建设生态文明,某工厂自2021年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分.下列选项错误的是 ( )
A. 4月份的利润为50万元
B. 治污改造完成后每月利润比前一个月增加30万元
C. 治污改造完成前后共有4个月的利润低于100万元
D. 9月份该厂利润达到200万元
6. 学校锅炉旁建有一个储煤库,开学初购进一批煤,现在知道:按每天用煤0.6吨计算,一学期(按150天计算)刚好用完.若每天的耗煤量为0.5吨,那么这批煤能维持 天.?
7. 在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,p=50,则当p=25时,V= .?
8. 电压一定时,电流与电阻成反比,I=的图象过点(1,36),当I=18 A,则R的值为 Ω.?
9. 在照明系统模拟控制电路实验中,研究人员发现光敏电阻值R(单位:Ω)与光照度E(单位:lx)之间成反比例函数关系,部分数据如下表所示:
光照度E/lx 0.5 1 1.5 2 2.5 3
光敏电阻值R/Ω 60 30 20 15 12 10
则光敏电阻值R与光照度E的函数表达式为 .?
10. 随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当x≥10时,y与x成反比例函数关系,当车速低于20千米/时时,交通就会拥堵.为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是 .?
11. 秋季是传染病的高发季节.为预防传染病,某学校会定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10 min燃烧完,此时教室内每立方米空气中的含药量为6 mg.研究表明当每立方米空气中的含药量不低于1.2 mg时,消毒才有效,则这次有效的消毒时间是 min.?
12. 湖州市菱湖镇某养鱼专业户准备挖一个面积为2000平方米的长方形鱼塘.
(1)求鱼塘的长y(米)关于宽x(米)的函数表达式;
(2)由于受场地的限制,鱼塘的宽最多只能挖20米,当鱼塘的宽是20米时,鱼塘的长为多少米?
13. 在对某物体做功一定的情况下,力F(N)与物体在力的方向上移动的距离s(m)成反比例函数关系,且当s=10 m时,F=3 N.
(1)试确定F(N)与s(m)之间的函数表达式;
(2)求当力F=15 N时,物体在力的方向上移动的距离s.
14. 已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时).
(1)求v关于t的函数表达式;
(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?
15. 某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB,BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10 ℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?
参 考 答 案
1. D 2. C 3. C 4. C 5. C
6. 180
7. 400
8. 2
9. R=
10. 0
12. 解:(1)由长方形面积为2000平方米,得到xy=2000,即y=.
(2)当x=20时,y==100,则当鱼塘的宽是20米时,鱼塘的长为100米.
13. 解:(1)设F=,由当s=10时,F=3,得3=,k=30,∴F与s之间的函数表达式是F=.
(2)当力F=15时,15=,s=2,即物体在力的方向上移动的距离为2 m.
14. 解:(1)由题意可得100=vt,∴v=.
(2)∵不超过5小时卸完船上的这批货物,∴t≤5,∴v≥=20. 答:平均每小时至少要卸货20吨.
15. 解:(1)设线段AB的函数表达式为y=k1x+b(k≠0),∵线段AB过点(0,10),(2,14),代入得 解得 ∴线段AB的函数表达式为y=2x+10(0≤x<5). ∵点B在线段AB上,当x=5时,y=20,∴点B的坐标为(5,20),∴线段BC的函数表达式为y=20(5≤x<10). 设双曲线CD的函数表达式为y=(k2≠0),∵点C的坐标为(10,20),∴k2=200,∴双曲线CD的函数表达式为y=(10≤x≤24),∴y关于x的函数表达式为y=
(2)由(1)得恒温系统设定的恒定温度为20 ℃.
(3)把y=10代入y=中,解得x=20,∴20-10=10. 答:恒温系统最多可以关闭10小时.
_21?????????è?????(www???21cnjy???com)_
