【沪科版九年级数学上册课时作业】21.6 综合与实践 获取最大利润(含答案)
文档属性
| 名称 | 【沪科版九年级数学上册课时作业】21.6 综合与实践 获取最大利润(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 292.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 16:11:48 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
沪科版九年级数学上册课时作业
第21章 二次函数与反比例函数
21.6 综合与实践 获取最大利润
1. 某鞋帽专卖店销售一种绒帽,若这种帽子每天获利y(元)与销售单价x(元)满足关系y=-x2+70x-800,要想获得最大利润,则销售单价为 ( )
A. 30元 B. 35元 C. 40元 D. 45元
2. 某大学生利用课余时间在网上销售一种成本为50元/件的商品,每月的销售量y(件)与销售单价x(元)之间的函数关系式为y=-4x+440.要获得最大利润,该商品的销售单价应定为 ( )
A. 60元 B. 70元 C. 80元 D. 90元
3. 某工厂年产值为150万元,经测算每增加100万元的投资,年产值可增加250万元.设新增加的投资为x万元,增加投资后的年产值为y万元,则y与x的关系式为 .?
4. 某商品的销售利润与销售单价存在二次函数关系,且二次项系数a=-1.当商品单价为160元和200元时,能获得同样多的利润,要使销售商品利润最大,销售单价应定为 元.?
5. 某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 甲 乙
进价(元/件) 40 90
售价(元/件) 60 120
设其中甲种商品购进x件,商场售完这批商品的总利润为y元.
(1)写出y关于x的函数表达式.
(2)该商场计划最多投入8000元用于购买这两种商品,则至少要购进多少件甲种商品?若销售完这些商品,则商场可获得的最大利润是多少元?
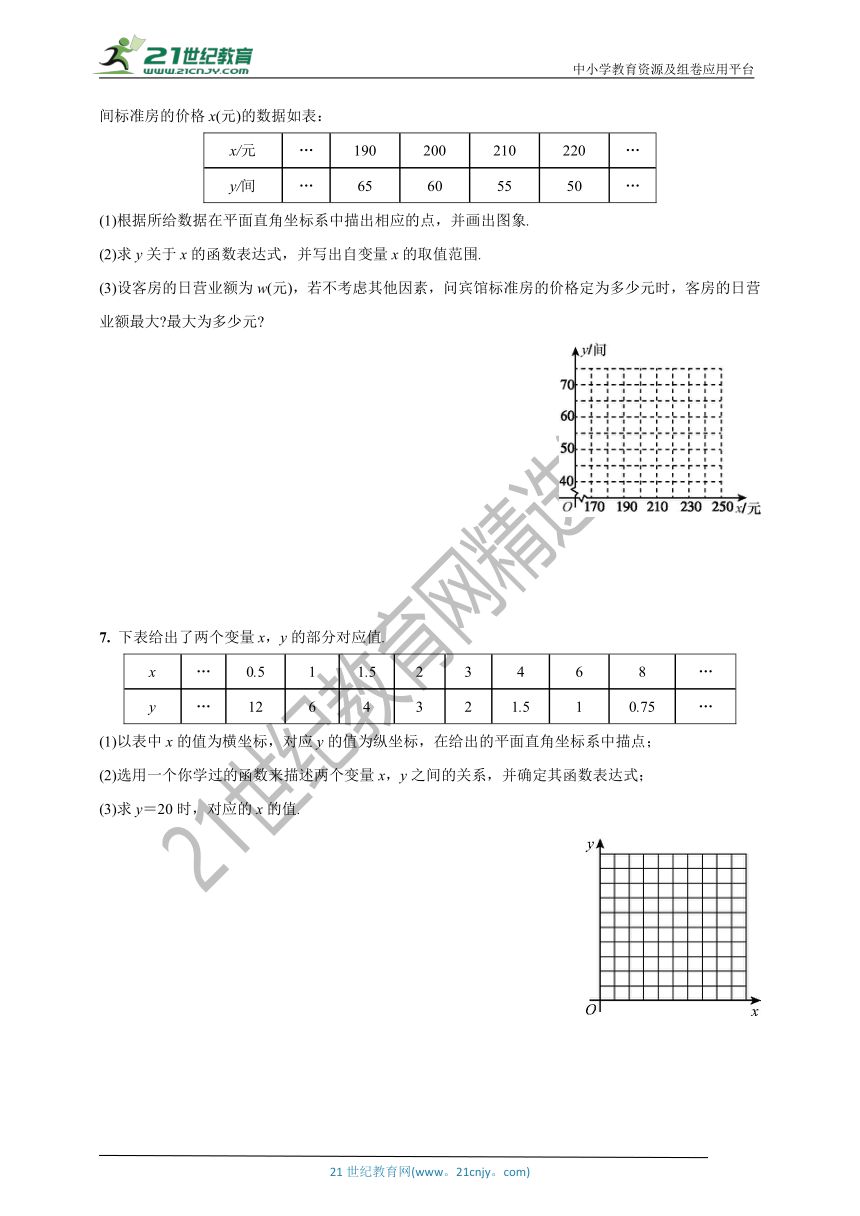
6. 某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间.经市场调查表明,该宾馆每间标准房的价格在170~240元之间(含170元,240元)浮动时,每天入住的房间数y(间)与每间标准房的价格x(元)的数据如表:
x/元 … 190 200 210 220 …
y/间 … 65 60 55 50 …
(1)根据所给数据在平面直角坐标系中描出相应的点,并画出图象.
(2)求y关于x的函数表达式,并写出自变量x的取值范围.
(3)设客房的日营业额为w(元),若不考虑其他因素,问宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?
7. 下表给出了两个变量x,y的部分对应值.
x … 0.5 1 1.5 2 3 4 6 8 …
y … 12 6 4 3 2 1.5 1 0.75 …
(1)以表中x的值为横坐标,对应y的值为纵坐标,在给出的平面直角坐标系中描点;
(2)选用一个你学过的函数来描述两个变量x,y之间的关系,并确定其函数表达式;
(3)求y=20时,对应的x的值.
8. A市和B市分别有某种库存机器12台和6台,现决定支援C村10台,D村8台.已知从A市调运一台机器到C村和D村的运费分别是400元和800元,从B市调运一台机器到C村和D村的运费分别是300元和500元.
(1)设B市运往C村机器x台,求总运费W关于x的函数关系式.
(2)若要求总运费不超过9200元,共有几种调运方案?
(3)在(2)的条件下,写出总运费最低的调运方案,最低总运费是多少元?
9. 我市某乡镇在“精准扶贫”活动中销售一种农产品,经分析发现月销售量y(万件)与月份x(月)的关系为y= 每件产品的利润z(元)与月份x(月)的关系如下表:
x 1 2 3 4 5 6 7 8 9 10 11 12
z 19 18 17 16 15 14 13 12 11 10 10 10
(1)请你根据表格求出每件产品的利润z(元)与月份x(月)的关系式;
(2)若月利润w(万元)=当月销售量y(万件)×当月每件产品的利润z(元),求月利润w(万元)与月份x(月)的关系式;
(3)当x为何值时,月利润w有最大值,最大值为多少?
参 考 答 案
1. B 2. C
3. y=2.5x+150
4. 180
5. 解:(1)由题意得y=(60-40)x+(120-90)(100-x)=-10x+3000(0(2)由已知得40x+90(100-x)≤8000,解得x≥20,∵-10<0,∴y随x的增大而减小,∴当x=20时,y有最大值,最大值为-10×20+3000=2800. 答:至少要购进20件甲种商品,若销售完这些商品,该商场获得的最大利润为2800元.
6. 解:(1)图略.
(2)设y=kx+b(k≠0),把(200,60)和(220,50)代入,得 解得 ∴y=-x+160(170≤x≤240).
(3)w=x·y=x(-x+160)=-x2+160x. ∵a=-<0,对称轴为直线x=-=160,∴在170≤x≤240范围内,w随x的增大而减小. ∴当价格x=170元时,日营业额w有最大值,最大值为12750元.
7. 解:(1)描点略.
(2)观察这些点的排列规律,可用反比例函数描述两个变量x,y之间的关系.设y=,∵点(2,3)在函数图象上,∴3=,k=6,∴函数表达式为y=.
(3)当y=20时,20=,∴x=0.3.
8. 解:(1)根据题意,得W=300x+500(6-x)+400(10-x)+800[12-(10-x)]=200x+8600.
(2)∵总运费不超过9200元,∴W=200x+8600≤9200,解得x≤3. ∵0≤x≤6,∴0≤x≤3,∴x=0,1,2,3,∴共有四种调运方案.
(3)∵0≤x≤3,且W=200x+8600,∴W随x的增大而增大,∴当x=0时,W的值最小,最小值为8600元,此时的调运方案是:B市运往C村0台,运往D村6台,A市运往C村10台,运往D村2台,最低总运费为8600元.
9. 解:(1)当1≤x≤9时,设每件产品的利润z(元)与月份x(月)的关系式为z=kx+b,则有 解得 即当1≤x≤9时,每件产品的利润z(元)与月份x(月)的关系式为z=-x+20. 当10≤x≤12时,z=10. 综上,z=
(2)当1≤x≤8时,w=(x+4)(-x+20)=-x2+16x+80,当x=9时,w=(-9+20)×(-9+20)=121,当10≤x≤12时,w=(-x+20)×10=-10x+200,综上所述,w=
(3)当1≤x≤8时,w=-x2+16x+80=-(x-8)2+144,∴当x=8时,w取得最大值,此时w=144;当x=9时,w=121;当10≤x≤12时,则当x=10时,w取得最大值,此时w=100. 综上所述,当x为8时,月利润w有最大值,最大值为144万元.
_21?????????è?????(www???21cnjy???com)_
沪科版九年级数学上册课时作业
第21章 二次函数与反比例函数
21.6 综合与实践 获取最大利润
1. 某鞋帽专卖店销售一种绒帽,若这种帽子每天获利y(元)与销售单价x(元)满足关系y=-x2+70x-800,要想获得最大利润,则销售单价为 ( )
A. 30元 B. 35元 C. 40元 D. 45元
2. 某大学生利用课余时间在网上销售一种成本为50元/件的商品,每月的销售量y(件)与销售单价x(元)之间的函数关系式为y=-4x+440.要获得最大利润,该商品的销售单价应定为 ( )
A. 60元 B. 70元 C. 80元 D. 90元
3. 某工厂年产值为150万元,经测算每增加100万元的投资,年产值可增加250万元.设新增加的投资为x万元,增加投资后的年产值为y万元,则y与x的关系式为 .?
4. 某商品的销售利润与销售单价存在二次函数关系,且二次项系数a=-1.当商品单价为160元和200元时,能获得同样多的利润,要使销售商品利润最大,销售单价应定为 元.?
5. 某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 甲 乙
进价(元/件) 40 90
售价(元/件) 60 120
设其中甲种商品购进x件,商场售完这批商品的总利润为y元.
(1)写出y关于x的函数表达式.
(2)该商场计划最多投入8000元用于购买这两种商品,则至少要购进多少件甲种商品?若销售完这些商品,则商场可获得的最大利润是多少元?
6. 某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间.经市场调查表明,该宾馆每间标准房的价格在170~240元之间(含170元,240元)浮动时,每天入住的房间数y(间)与每间标准房的价格x(元)的数据如表:
x/元 … 190 200 210 220 …
y/间 … 65 60 55 50 …
(1)根据所给数据在平面直角坐标系中描出相应的点,并画出图象.
(2)求y关于x的函数表达式,并写出自变量x的取值范围.
(3)设客房的日营业额为w(元),若不考虑其他因素,问宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?
7. 下表给出了两个变量x,y的部分对应值.
x … 0.5 1 1.5 2 3 4 6 8 …
y … 12 6 4 3 2 1.5 1 0.75 …
(1)以表中x的值为横坐标,对应y的值为纵坐标,在给出的平面直角坐标系中描点;
(2)选用一个你学过的函数来描述两个变量x,y之间的关系,并确定其函数表达式;
(3)求y=20时,对应的x的值.
8. A市和B市分别有某种库存机器12台和6台,现决定支援C村10台,D村8台.已知从A市调运一台机器到C村和D村的运费分别是400元和800元,从B市调运一台机器到C村和D村的运费分别是300元和500元.
(1)设B市运往C村机器x台,求总运费W关于x的函数关系式.
(2)若要求总运费不超过9200元,共有几种调运方案?
(3)在(2)的条件下,写出总运费最低的调运方案,最低总运费是多少元?
9. 我市某乡镇在“精准扶贫”活动中销售一种农产品,经分析发现月销售量y(万件)与月份x(月)的关系为y= 每件产品的利润z(元)与月份x(月)的关系如下表:
x 1 2 3 4 5 6 7 8 9 10 11 12
z 19 18 17 16 15 14 13 12 11 10 10 10
(1)请你根据表格求出每件产品的利润z(元)与月份x(月)的关系式;
(2)若月利润w(万元)=当月销售量y(万件)×当月每件产品的利润z(元),求月利润w(万元)与月份x(月)的关系式;
(3)当x为何值时,月利润w有最大值,最大值为多少?
参 考 答 案
1. B 2. C
3. y=2.5x+150
4. 180
5. 解:(1)由题意得y=(60-40)x+(120-90)(100-x)=-10x+3000(0
6. 解:(1)图略.
(2)设y=kx+b(k≠0),把(200,60)和(220,50)代入,得 解得 ∴y=-x+160(170≤x≤240).
(3)w=x·y=x(-x+160)=-x2+160x. ∵a=-<0,对称轴为直线x=-=160,∴在170≤x≤240范围内,w随x的增大而减小. ∴当价格x=170元时,日营业额w有最大值,最大值为12750元.
7. 解:(1)描点略.
(2)观察这些点的排列规律,可用反比例函数描述两个变量x,y之间的关系.设y=,∵点(2,3)在函数图象上,∴3=,k=6,∴函数表达式为y=.
(3)当y=20时,20=,∴x=0.3.
8. 解:(1)根据题意,得W=300x+500(6-x)+400(10-x)+800[12-(10-x)]=200x+8600.
(2)∵总运费不超过9200元,∴W=200x+8600≤9200,解得x≤3. ∵0≤x≤6,∴0≤x≤3,∴x=0,1,2,3,∴共有四种调运方案.
(3)∵0≤x≤3,且W=200x+8600,∴W随x的增大而增大,∴当x=0时,W的值最小,最小值为8600元,此时的调运方案是:B市运往C村0台,运往D村6台,A市运往C村10台,运往D村2台,最低总运费为8600元.
9. 解:(1)当1≤x≤9时,设每件产品的利润z(元)与月份x(月)的关系式为z=kx+b,则有 解得 即当1≤x≤9时,每件产品的利润z(元)与月份x(月)的关系式为z=-x+20. 当10≤x≤12时,z=10. 综上,z=
(2)当1≤x≤8时,w=(x+4)(-x+20)=-x2+16x+80,当x=9时,w=(-9+20)×(-9+20)=121,当10≤x≤12时,w=(-x+20)×10=-10x+200,综上所述,w=
(3)当1≤x≤8时,w=-x2+16x+80=-(x-8)2+144,∴当x=8时,w取得最大值,此时w=144;当x=9时,w=121;当10≤x≤12时,则当x=10时,w取得最大值,此时w=100. 综上所述,当x为8时,月利润w有最大值,最大值为144万元.
_21?????????è?????(www???21cnjy???com)_
