2021-2022学年人教版数学八年级上册 13.1 轴对称暑期学情跟踪练习(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册 13.1 轴对称暑期学情跟踪练习(word版含答案) | 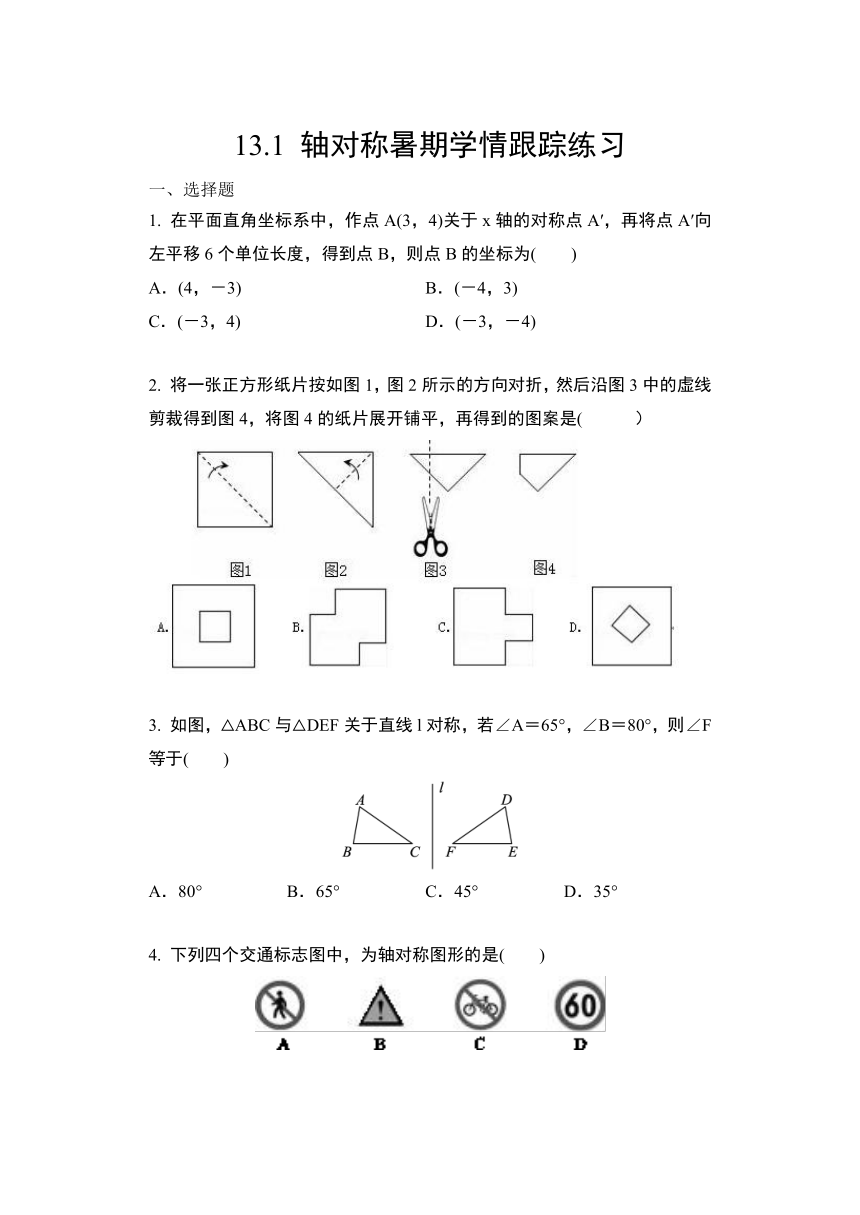 | |
| 格式 | docx | ||
| 文件大小 | 285.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 16:39:47 | ||
图片预览



文档简介
13.1 轴对称暑期学情跟踪练习
一、选择题
1. 在平面直角坐标系中,作点A(3,4)关于x轴的对称点A′,再将点A′向左平移6个单位长度,得到点B,则点B的坐标为( )
A.(4,-3) B.(-4,3)
C.(-3,4) D.(-3,-4)
2. 将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是( )
3. 如图,△ABC与△DEF关于直线l对称,若∠A=65°,∠B=80°,则∠F等于( )
A.80° B.65° C.45° D.35°
4. 下列四个交通标志图中,为轴对称图形的是( )
5. 如下图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A.①??? ? B.②??? ? C.⑤??? ? D.⑥
6. 点(1,3)关于x轴对称的点的坐标是 ( )
A.(1,-3) B.(-3,-1)
C.(-1,3) D.(-1,-3)
7. 如图,△ABC和△AB′C′关于直线l对称,下列结论中,错误的是( )
A.△ABC≌△AB′C′ B.∠BAC′=∠B′AC
C.l垂直平分点C,C′的连线 D.直线BC和B′C′的交点不在直线l上
8. 如图所示的五角星是轴对称图形,它的对称轴共有( )
A.1条 B.3条
C.5条 D.无数条
9. 如图,△ABC和△A′B′C′关于直线对称,下列结论中:正确的有( )
①△ABC≌△A′B′C′;②∠BAC′=∠B′AC;③l垂直平分CC′;
④直线BC和B′C′的交点不一定在l上,
A.4个 B.3个 C.2个 D.1个
10. 已知:在平面直角坐标系中,A(a,b)(b≠0),B(m,n).若a-m=4,b+n=0,则下列结论正确的是( )
A.把点A向左平移4个单位长度后,与点B关于x轴对称
B.把点A向右平移4个单位长度后,与点B关于x轴对称
C.把点A向左平移4个单位长度后,与点B关于y轴对称
D.把点A向右平移4个单位长度后,与点B关于y轴对称
11. 在数学课上,老师提出如下问题:如图,已知△ABC中,AB
二、填空题
12. 如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有 个.
13. 如图,点P在∠AOB内,M,N分别是点P关于OA,OB的对称点,连接MN交OA于点E,交OB于点F.若△PEF的周长是20 cm,则MN的长是________cm.
14. 若点A(1﹣m,6)与B(2+n,6)关于某坐标轴对称,则m﹣n= .
15. 如图,△ABO是关于y轴对称的轴对称图形,点A的坐标为(-2,3),则点B的坐标为________.
16. 如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.
三、解答题
17. 如图,在平面直角坐标系中,
(1)描出A(- 4,3)B(-1,0)C(-2,3)三点.
(2)△ABC的面积是????????
(3)作出△ABC关于x轴的对称图形.
18. 图中的两个图形关于某条直线对称,根据图中提供的条件求出x,y的值.
19. 如图,在△ABC中,边AC的垂直平分线分别交AB,AC于点E,D.
(1)若AC=8,△BEC的周长为18,求△ABC的周长;
(2)若AB-BC=6,△BEC的周长为16,求AB,BC的长.
20. 如图,Rt△ABC的顶点A,B,C关于直线MN的对称点分别为A',B',C',其中∠A=90°,AC=8 cm,点C,B,A'在同一条直线上,且A'C=12 cm.
(1)求△A'B'C'的周长;
(2)求△A'CC'的面积.
21. 如图,在四边形ABCD中,AB=AD,BC边的垂直平分线MN经过点A.求证:点A在线段CD的垂直平分线上.
22. 已知点A(2m+n,2),B (1,n﹣m),当m、n分别为何值时,
(1)A、B关于x轴对称;
(2)A、B关于y轴对称.
23. 如图,已知△ABC.
(1)用直尺和圆规分别作出AB,AC边的垂直平分线l1,l2;
(2)若直线l1,l2的交点为O,连接OB,OC.求证:OB=OC.
答案
一、选择题
1. D 2. B 3. D 4. B 5. B 6. A
7. D 8. C 9. B 10. A 11. C
二、填空题
12. 4 13. 20 14. 3 15. (2,3) 16. 13
三、解答题
17. (1)如图所示;(2)3;(3)如图所示
18. 解:x=∠ADC=360°-40°-95°-110°=115°,y=HG=3.
19. 解:(1)∵DE垂直平分AC,
∴CE=AE.
∵△BEC的周长为18,
∴BE+BC+CE=BE+AE+BC=AB+BC=18.
∴△ABC的周长=AB+BC+AC=18+8=26.
(2)∵△BEC的周长为16,
∴AB+BC=16.
又∵AB-BC=6,
∴AB=11,BC=5.
20. 解:(1)∵Rt△ABC的顶点A,B,C关于直线MN的对称点分别为A',B',C',AC=8 cm,A'C=8cm,
∴AB=A'B',AC=A'C',∠A'=∠A=90°.
∴△A'B'C'的周长为A'C'+B'C'+A'B'=AC+A'C=12+8=20(cm).
(2)由(1)得A'C'=AC=8 cm,∠A'=90°,
∴△A'CC'的面积为12A'C·A'C'=12×12×8=48(cm2).
21. 证明:连接AC.
∵点A在线段BC的垂直平分线MN上,
∴AB=AC.
∵AB=AD,∴AC=AD.
∴点 A在线段CD的垂直平分线上.
22. 解:
(1)∵点A(2m+n,2),B (1,n﹣m),A、B关于x轴对称,
∴,解得;
(2)∵点A(2m+n,2),B (1,n﹣m),A、B关于y轴对称,
∴,解得:.
23. 解:(1)如图所示.
(2)证明:如图,连接OA.
∵l1是AB的垂直平分线,∴OA=OB.
同理,OA=OC.∴OB=OC.
解:(1)如图所示.
(2)证明:如图,连接OA.
∵l1是AB的垂直平分线,∴OA=OB.
同理,OA=OC.∴OB=OC.
一、选择题
1. 在平面直角坐标系中,作点A(3,4)关于x轴的对称点A′,再将点A′向左平移6个单位长度,得到点B,则点B的坐标为( )
A.(4,-3) B.(-4,3)
C.(-3,4) D.(-3,-4)
2. 将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是( )
3. 如图,△ABC与△DEF关于直线l对称,若∠A=65°,∠B=80°,则∠F等于( )
A.80° B.65° C.45° D.35°
4. 下列四个交通标志图中,为轴对称图形的是( )
5. 如下图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A.①??? ? B.②??? ? C.⑤??? ? D.⑥
6. 点(1,3)关于x轴对称的点的坐标是 ( )
A.(1,-3) B.(-3,-1)
C.(-1,3) D.(-1,-3)
7. 如图,△ABC和△AB′C′关于直线l对称,下列结论中,错误的是( )
A.△ABC≌△AB′C′ B.∠BAC′=∠B′AC
C.l垂直平分点C,C′的连线 D.直线BC和B′C′的交点不在直线l上
8. 如图所示的五角星是轴对称图形,它的对称轴共有( )
A.1条 B.3条
C.5条 D.无数条
9. 如图,△ABC和△A′B′C′关于直线对称,下列结论中:正确的有( )
①△ABC≌△A′B′C′;②∠BAC′=∠B′AC;③l垂直平分CC′;
④直线BC和B′C′的交点不一定在l上,
A.4个 B.3个 C.2个 D.1个
10. 已知:在平面直角坐标系中,A(a,b)(b≠0),B(m,n).若a-m=4,b+n=0,则下列结论正确的是( )
A.把点A向左平移4个单位长度后,与点B关于x轴对称
B.把点A向右平移4个单位长度后,与点B关于x轴对称
C.把点A向左平移4个单位长度后,与点B关于y轴对称
D.把点A向右平移4个单位长度后,与点B关于y轴对称
11. 在数学课上,老师提出如下问题:如图,已知△ABC中,AB
二、填空题
12. 如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有 个.
13. 如图,点P在∠AOB内,M,N分别是点P关于OA,OB的对称点,连接MN交OA于点E,交OB于点F.若△PEF的周长是20 cm,则MN的长是________cm.
14. 若点A(1﹣m,6)与B(2+n,6)关于某坐标轴对称,则m﹣n= .
15. 如图,△ABO是关于y轴对称的轴对称图形,点A的坐标为(-2,3),则点B的坐标为________.
16. 如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.
三、解答题
17. 如图,在平面直角坐标系中,
(1)描出A(- 4,3)B(-1,0)C(-2,3)三点.
(2)△ABC的面积是????????
(3)作出△ABC关于x轴的对称图形.
18. 图中的两个图形关于某条直线对称,根据图中提供的条件求出x,y的值.
19. 如图,在△ABC中,边AC的垂直平分线分别交AB,AC于点E,D.
(1)若AC=8,△BEC的周长为18,求△ABC的周长;
(2)若AB-BC=6,△BEC的周长为16,求AB,BC的长.
20. 如图,Rt△ABC的顶点A,B,C关于直线MN的对称点分别为A',B',C',其中∠A=90°,AC=8 cm,点C,B,A'在同一条直线上,且A'C=12 cm.
(1)求△A'B'C'的周长;
(2)求△A'CC'的面积.
21. 如图,在四边形ABCD中,AB=AD,BC边的垂直平分线MN经过点A.求证:点A在线段CD的垂直平分线上.
22. 已知点A(2m+n,2),B (1,n﹣m),当m、n分别为何值时,
(1)A、B关于x轴对称;
(2)A、B关于y轴对称.
23. 如图,已知△ABC.
(1)用直尺和圆规分别作出AB,AC边的垂直平分线l1,l2;
(2)若直线l1,l2的交点为O,连接OB,OC.求证:OB=OC.
答案
一、选择题
1. D 2. B 3. D 4. B 5. B 6. A
7. D 8. C 9. B 10. A 11. C
二、填空题
12. 4 13. 20 14. 3 15. (2,3) 16. 13
三、解答题
17. (1)如图所示;(2)3;(3)如图所示
18. 解:x=∠ADC=360°-40°-95°-110°=115°,y=HG=3.
19. 解:(1)∵DE垂直平分AC,
∴CE=AE.
∵△BEC的周长为18,
∴BE+BC+CE=BE+AE+BC=AB+BC=18.
∴△ABC的周长=AB+BC+AC=18+8=26.
(2)∵△BEC的周长为16,
∴AB+BC=16.
又∵AB-BC=6,
∴AB=11,BC=5.
20. 解:(1)∵Rt△ABC的顶点A,B,C关于直线MN的对称点分别为A',B',C',AC=8 cm,A'C=8cm,
∴AB=A'B',AC=A'C',∠A'=∠A=90°.
∴△A'B'C'的周长为A'C'+B'C'+A'B'=AC+A'C=12+8=20(cm).
(2)由(1)得A'C'=AC=8 cm,∠A'=90°,
∴△A'CC'的面积为12A'C·A'C'=12×12×8=48(cm2).
21. 证明:连接AC.
∵点A在线段BC的垂直平分线MN上,
∴AB=AC.
∵AB=AD,∴AC=AD.
∴点 A在线段CD的垂直平分线上.
22. 解:
(1)∵点A(2m+n,2),B (1,n﹣m),A、B关于x轴对称,
∴,解得;
(2)∵点A(2m+n,2),B (1,n﹣m),A、B关于y轴对称,
∴,解得:.
23. 解:(1)如图所示.
(2)证明:如图,连接OA.
∵l1是AB的垂直平分线,∴OA=OB.
同理,OA=OC.∴OB=OC.
解:(1)如图所示.
(2)证明:如图,连接OA.
∵l1是AB的垂直平分线,∴OA=OB.
同理,OA=OC.∴OB=OC.
