2021—2022学年人教版数学九年级上册24.4 弧长和扇形面积 同步测试(word含答案)
文档属性
| 名称 | 2021—2022学年人教版数学九年级上册24.4 弧长和扇形面积 同步测试(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 539.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 16:58:10 | ||
图片预览



文档简介
11709400112141002021人教版九年级上册数学第二十四章 24.4 弧长和扇形面积 同步测试
(总分:120分 考试时间:120分钟)
一、选择题(36分)
(3分)在半径为 1 的圆中,弧长等于 2π3 的弧所对的圆心角是 ??
A. 30? B. 60? C. 120? D. 150?
(3分)如果 ⊙O 的半径为 3,扇形的面积为 3π,则扇形的圆心角度数是 ??
A. 150? B. 120? C. 60? D. 45?
(3分)如图,有一圆 O 通过 △ABC 的三个顶点.若 ∠B=75?,∠C=60?,且 BC 的长度为 4π,则 BC 的长度为 ??
A.8 B.82 C.16 D.162
(3分)如图,以 AB 为直径,点 O 为圆心的半圆经过点 C,若 AC=BC=2,则图中阴影部分的面积是 ??
A.π4 B.12+π4 C.π2 D.12+π2
(3分)半径为 6,圆心角为 120? 的扇形的面积是 ??
A.3π B.6π C.9π D.12π
(3分)如图,AB 是 ⊙O 的直径,AB=4,CD 是 ⊙O 的切线,切点为 D,CD 与 AB 的延长线交于点 C,若 ∠A=∠C,则 BD 的长为 ??
A. 13π B. 23π C. 43π D. 83π
(3分)如图,AB 是 ⊙O 的直径,CD⊥AB,∠ABD=60?,CD=23,则阴影部分的面积为 ??
A. 23π B. π C. 2π D. 4π
(3分)已知圆锥的底面半径为 3?cm,母线长为 4?cm,则圆锥的全面积是 ??
A. 15π?cm2 B. 21π?cm2 C. 20π?cm2 D. 24π?cm2
(3分)如图,已知点 C,D 是以 AB 为直径的半圆的三等分点,弧 CD 的长为 13π,则图中阴影部分的面积为 ??
A. 16π B. 316π C. 124π D. 112π+34
(3分)已知扇形的圆心角为 45?,半径长为 12,则该扇形的弧长为 ??
A. 3π4 B. 2π C. 3π D. 12π
(3分)一个扇形的圆心角是 120?,面积为 3π?cm2,那么这个扇形的半径是 ??
A.1?cm B.3?cm C.6?cm D.9?cm
(3分)如图,AB 是 ⊙O 的直径,M,N 是 AB(异于 A,B)上两点,C 是 MN 上一动点,∠ACB 的平分线交 ⊙O 于点 D,∠BAC 的平分线交 CD 于点 E.当点 C 从点 M 运动到点 N 时,则 C,E 两点的运动路径长的比是 ??
A. 2 B. π2 C. 32 D. 52
二、填空题(24分)
(3分)如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥底面圆的半径 r=2?cm,扇形的圆心角 θ=120?,则该圆锥的母线长 l 为 cm.
(3分)用半径为 30,圆心角为 120? 的扇形纸片围成一个圆锥的侧面,那么这个圆锥的底面圆半径是 .
(3分)如图,AB 是 ⊙O 的直径,点 C 在 ⊙O 上,连接 AC,BC,∠ACB 的平分线 CD 交 ⊙O 于点 D,若 ⊙O 的半径是 4,则 AD 的长是 .
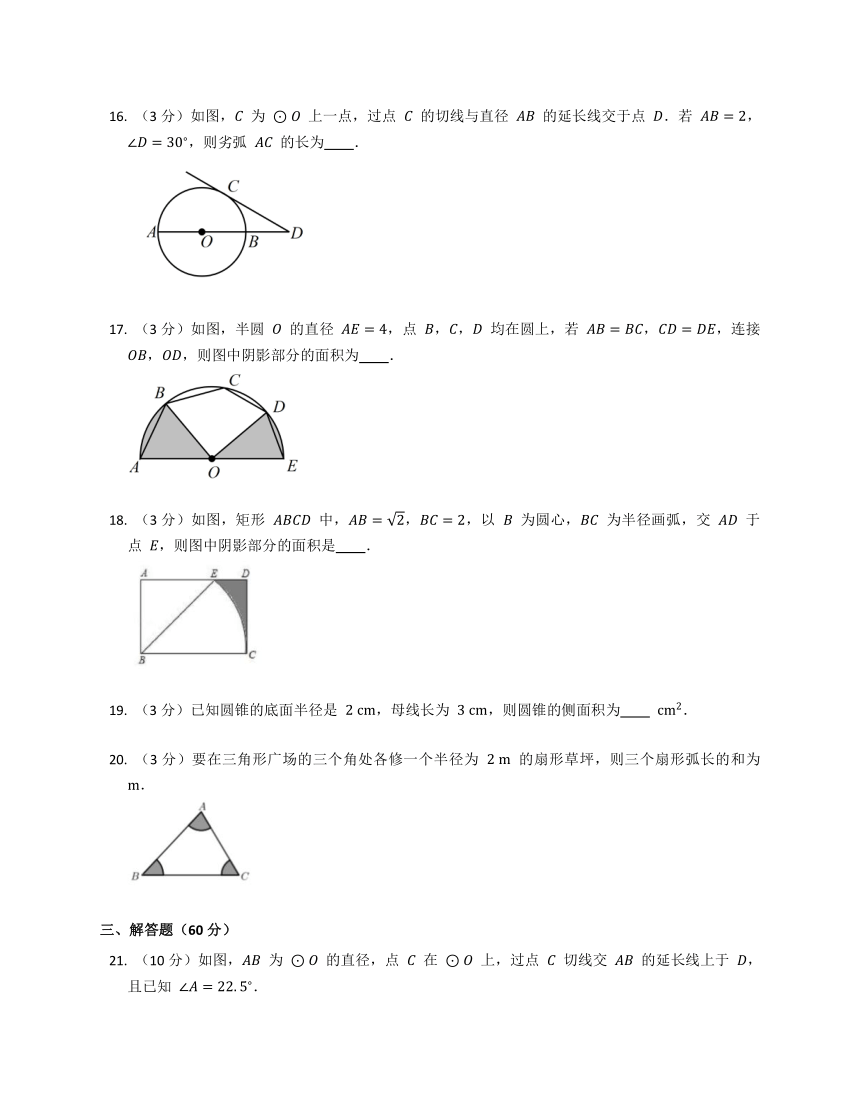
(3分)如图,C 为 ⊙O 上一点,过点 C 的切线与直径 AB 的延长线交于点 D.若 AB=2,∠D=30?,则劣弧 AC 的长为 .
(3分)如图,半圆 O 的直径 AE=4,点 B,C,D 均在圆上,若 AB=BC,CD=DE,连接 OB,OD,则图中阴影部分的面积为 .
(3分)如图,矩形 ABCD 中,AB=2,BC=2,以 B 为圆心,BC 为半径画弧,交 AD 于点 E,则图中阴影部分的面积是 .
(3分)已知圆锥的底面半径是 2?cm,母线长为 3?cm,则圆锥的侧面积为 cm2.
(3分)要在三角形广场的三个角处各修一个半径为 2?m 的扇形草坪,则三个扇形弧长的和为 m.
三、解答题(60分)
(10分)如图,AB 为 ⊙O 的直径,点 C 在 ⊙O 上,过点 C 切线交 AB 的延长线上于 D,且已知 ∠A=22.5?.
(1) 求 ∠D 的度数;
(2) 若弦 CF⊥AB,垂足为 E,且 CF=2,求图中阴影部分的面积.
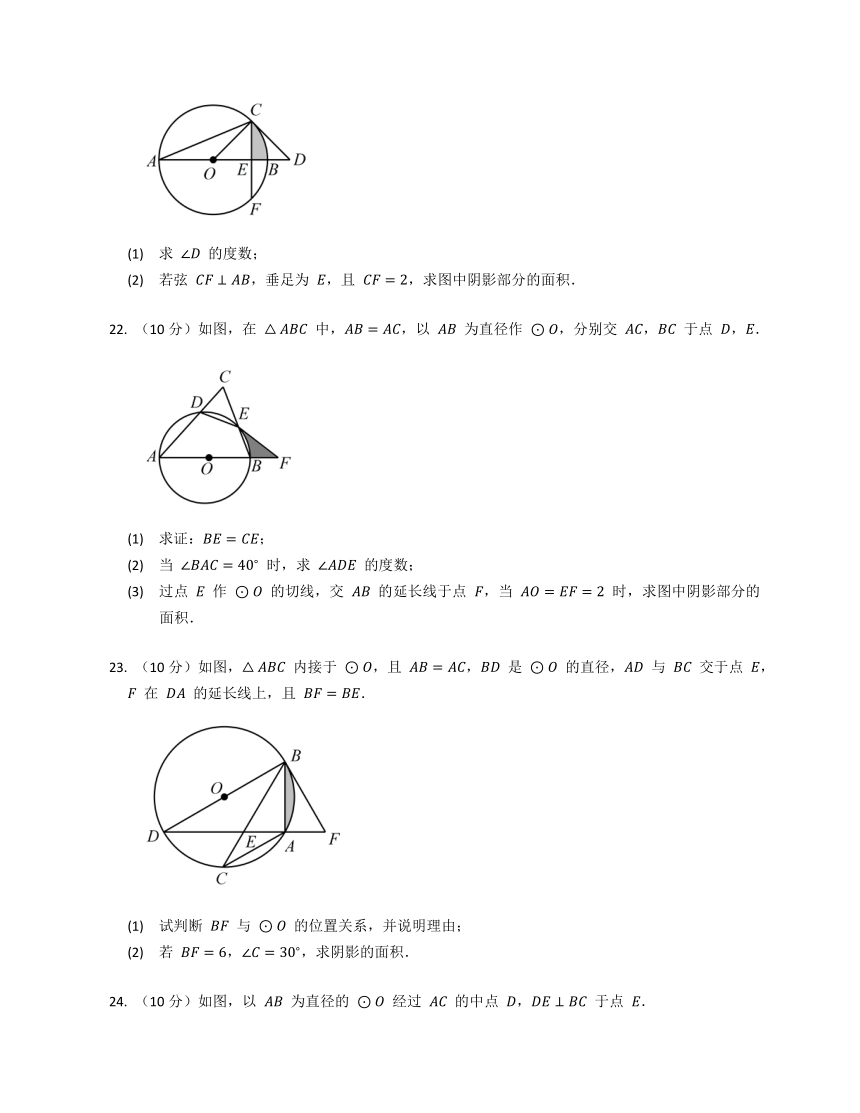
(10分)如图,在 △ABC 中,AB=AC,以 AB 为直径作 ⊙O,分别交 AC,BC 于点 D,E.
(1) 求证:BE=CE;
(2) 当 ∠BAC=40? 时,求 ∠ADE 的度数;
(3) 过点 E 作 ⊙O 的切线,交 AB 的延长线于点 F,当 AO=EF=2 时,求图中阴影部分的面积.
(10分)如图,△ABC 内接于 ⊙O,且 AB=AC,BD 是 ⊙O 的直径,AD 与 BC 交于点 E,F 在 DA 的延长线上,且 BF=BE.
(1) 试判断 BF 与 ⊙O 的位置关系,并说明理由;
(2) 若 BF=6,∠C=30?,求阴影的面积.
(10分)如图,以 AB 为直径的 ⊙O 经过 AC 的中点 D,DE⊥BC 于点 E.
(1) 求证:DE 是 ⊙O 的切线;
(2) 当 DE=1,∠C=30? 时,求图中阴影部分的面积.
(10分)如图,⊙O 的直径 AB 与弦 CD 相交于点 E,且 DE=CE,⊙O 的切线 BF 与弦 AD 的延长线交于点 F.
(1) 求证:CD∥BF;
(2) 若 ⊙O 的半径为 6,∠A=35?,求 DBC 的长.
(10分)如图,在 △ABC 中,AB=AC,以 AB 为直径的 ⊙O 分别与 BC,AC 交于点 D,E,过点 D 作 ⊙O 的切线 DF,交 AC 于点 F.
(1) 求证:DF⊥AC;
(2) 若 ⊙O 的半径为 4,∠CDF=22.5?,求阴影部分的面积.
答案
一、选择题(36分)
1. 【答案】C
【解析】设圆心角为 n?
∵1=nπr180,r=1,
∴nπ×1180=2π3,解得 n=120?.
【知识点】弧长的计算
2. 【答案】B
【解析】 S=nπr2360=nπ×9360=3π,
解得 n=120.
【知识点】扇形面积的计算
3. 【答案】B
【知识点】弧长的计算
4. 【答案】A
【解析】本题考查扇形面积的计算.∵AB 为直径,∴∠ACB=90?.
∵AC=BC=2,∴△ACB 为等腰直角三角形,∴OC⊥AB,∴△AOC 和 △BOC 都是等腰直角三角形,∴S△AOC=S△BOC,OA=22AC=1,∴S阴影部分=S扇形AOC=90×π×12360=π4.
【知识点】扇形面积的计算、圆周角定理及其推理
5. 【答案】D
【解析】根据扇形面积公式得 S=120360π×62=12π.
【知识点】扇形面积的计算
6. 【答案】B
【解析】如图,连接 OD,
∵CD 是 ⊙O 的切线,
∴OD⊥CD,
∴∠ODC=90?,
∴∠COD+∠C=90?,
∵∠A=∠C,∠COD=2∠A,
∴∠COD=2∠C,
∴3∠C=90?,
∴∠C=30?,
∴∠COD=2∠C=60?,
∵AB=4,
∴OB=2,
∴BD 的长为 60π×2180=23π.
【知识点】弧长的计算、切线的性质
7. 【答案】A
【解析】连接 OD.
∵CD⊥AB,
∴CE=DE=12CD=3,
故 S△OCE=S△ODE,即可得阴影部分的面积等于扇形 OBD 的面积,
又 ∵∠ABD=60?,
∴∠CDB=30?,
∴∠COB=60?,
∴OC=2,
∴S扇形OBD=60π×22360=2π3,即阴影部分的面积为 2π3.
【知识点】扇形面积的计算
8. 【答案】B
【解析】这个圆锥的底面圆的面积 =π?32=9π,
圆锥的侧面积 =12?2π?3?4=12π,
所以圆锥的全面积 =9π+12π=21πcm2.
【知识点】圆锥的计算
9. 【答案】A
【解析】连接 CD,OC,OD.
∵C,D 是以 AB 为直径的半圆周的三等分点,
∴∠AOC=∠COD=∠DOB=60?,AC=CD,
∵ 弧 CD 的长为 13π,
∴60π?r180=13π,解得:r=1,
又 ∵OA=OC=OD,
∴△OAC,△OCD 是等边三角形,
在 △OAC 和 △OCD 中,
OA=OC,OC=OD,AC=CD,
∴△OAC≌△OCDSSS,
∴S阴影=S扇形OCD=60π?12360=π6.
【知识点】扇形面积的计算
10. 【答案】C
【解析】根据弧长公式:l=45?π?12180=3π.
【知识点】弧长的计算
11. 【答案】B
【解析】设扇形的半径为 R,由题意:3π=120π?R2360,
解得 R=±3,
∵ R>0,
∴ R=3?cm,
∴ 这个扇形的半径为 3?cm.
【知识点】扇形面积的计算
12. 【答案】A
【解析】方法一:
如图,连接 EB.
设 OA=r.
∵AB 是直径,
∴∠ACB=90?,
∵E 是 △ACB 的内心,
∴∠AEB=135?,
∵∠ACD=∠BCD,
∴AD=DB,
∴AD=DB,
∴∠ADB=90?,
易知点 E 在以 D 为圆心 DA 为半径的圆上,运动轨迹是 GF,点 C 的运动轨迹是 MN,
∵∠MON=2∠GDF,设 ∠GDF=α,则 ∠MON=2α,
∴MNGF=2α?π?r180α?π?2r180=2.
方法二:
如图所示,连接 AD,BD,
∵ 点 E 是 ∠ACB 的平分线与 ∠BAC 的平分线的交点,
∴∠ACD=∠BCD,∠CAE=∠BAE.
∵∠BAD=∠BCD,
∴∠BAD+∠BAE=∠ACD+∠CAE,即 ∠DAE=∠AED,
∴AD=ED,
∴ 点 E 在以 D 为圆心,以 AD 为半径的圆上.
又 ∵AB 是 ⊙O 的直径,CD 是 ∠ACB 的平分线,
∴AD=BD,
∴AD=BD.
设 ⊙ 的半径为 r,
∴AD=2r,
∴ 点 E 的运动路径长是 90π?2r180=22πr.
∵ 点 C 是 MN 上一动点,
∴ 点 C 的运动路径长是 πr,
∴C,E 两点的运动路径长的比是 πr:22πr=2:1.
【知识点】弧长的计算
二、填空题(24分)
13. 【答案】6
【解析】根据题意,得 120πl180=2π×2,解得 l=6.
【知识点】圆锥的计算
14. 【答案】10
【解析】设圆锥底面圆的半径为 r,
则 2πr=120π×30180,
解得:r=10,
故圆锥的底面半径为 10.
【知识点】圆锥的计算
15. 【答案】 2π
【知识点】弧长的计算
16. 【答案】 23π
【知识点】弧长的计算、切线的性质
17. 【答案】π
【解析】连接 OC.
因为 AB=BC,CD=DE,
所以 AB=BC,CD=DE,
所以 ∠AOB=∠BOC,∠COD=∠DOE.
因为 ∠AOB+∠BOC+∠COD+∠DOE=180?,
所以 ∠AOB+∠DOE=90?.
因为直径 AE=4,
所以图中阴影部分的面积为 90?π?22360?=π.
【知识点】扇形面积的计算
18. 【答案】 22?1?π2
【解析】解:因为矩形 ABCD 中,AB=2,BC=2,
所以 AD=BC=2,CD=AB=2,∠A=90?,
因为 BE=BC=2,
在 Rt△ABE 中,AE=BE2?AB2=22?22=2,
所以 AB=AE,
所以 ∠ABE=∠EBC=45?,所以
S阴=S四边形BCDE?S扇形BEC=12×2+2?2×2?45?π?22360=22?1?π2,
故答案为 22?1?π2.
【知识点】扇形面积的计算
19. 【答案】 6π
【解析】底面半径是 2?cm,则底面周长 =4π?cm,圆锥的侧面积 =12×4π×3=6π?cm2.
【知识点】圆锥的计算
20. 【答案】 2π
【解析】设 △ABC 的三个内角的度数分别为 α,β,γ,
则 α+β+γ=180?,
三个扇形的弧长和为:
a×π×2180+β×π×2180+γ×π×2180=2π.
故答案为:2π.
【知识点】弧长的计算
三、解答题(60分)
21. 【答案】
(1) 略.
(2) 略.
【知识点】切线的性质、垂径定理、扇形面积的计算
22. 【答案】
(1) 连接 AE.
∵ AB 为 ⊙O 的直径,
∴ ∠AEB=90?,
∴ AE⊥BC.
∵ AB=AC,
∴ BE=CE.
(2) 由(1)得 ∠BAE=12×40?=20?,
∴ ∠ABE=70?,
∴ ∠ADE=∠EBF=180??70?=110?.
(3) 连接 OE.
∵ EF 切 ⊙O 于点 E,
∴ OE⊥EF.
∵ AO=EF=OE=2,
∴ ∠BOE=45?,
∴S阴影=S△OEF?S扇形OBE=12×2×2?45×π×22360=2?π2.
【知识点】扇形面积的计算、圆周角定理推论、切线的性质、圆内接四边形的性质
23. 【答案】
(1) BF 与 ⊙O 的位置关系是相切.
证明:
∵∠D 和 ∠C 都对弧 AB,
∴∠C=∠D.
∵BD 是直径,
∴∠DAB=90?.
∴∠D+∠ABD=90?.
∴∠C+∠ABD=90?.
∵∠DAB=90?,
∴BA⊥EF.
∵BE=BF,
∴∠EBA=∠FBA.
∵AB=AC,
∴∠C=∠EBA=∠FBA.
∵∠C+∠ABD=90?,
∴∠FBA+∠ABD=90?.
∴∠FBD=90?,
∵OB 是半径,
∴BF 是 ⊙O 的切线.
(2) 连接 OA.
∵∠C=∠D=30?=∠FBA,
∴ 在 Rt△ABF 中,BF=6,AF=BF=3.
由勾股定理得 AB=33.
在 Rt△DBA 中,∠D=30?,
∴BD=2AB=63,OB=33,∠BOA=2∠C=60?.
∵ 在 Rt△ABD 中,BD=63,AB=33,由勾股定理得:AD=9.
∵BO=OD,
∴S△BOA=S△AOD=12S△ABD=12×12×33×9=2734.
∴S阴影=S扇形OBA?S△OAB=60π×332360?2734=9π2?2734.
【知识点】扇形面积的计算、切线的判定
24. 【答案】
(1) 连接 OD.
∵AB 是 ⊙O 的直径,D 是 AC 的中点,
∴OD 是 △ABC 的中位线.
∴OD∥BC.
∵DE⊥BC,
∴OD⊥DE.
∵ 点 D 在圆上,
∴DE 为 ⊙O 的切线.
(2) ∵∠C=30?,DE=1,∠DEC=90?,
∴DC=2.
∵OD∥BC,
∴∠ODA=30?.
∵OD=OA,
∴∠OAD=∠ODA=30?,
∴∠AOD=120?,
∴OA=233,
∴ 阴影部分面积 S=120?π×2332360?12×2×33=4π9?33.
【知识点】扇形面积的计算、切线的判定
25. 【答案】
(1) 证明:∵AB 是 ⊙O 的直径,DE=CE,
∴AB⊥CD,
∵BF 是 ⊙O 的切线,
∴AB⊥BF,
∴CD∥BF;
(2) 连接 OD,OC,
∵∠A=35?,
∴BOD=2∠A=70?,
∴COD=2∠BOD=140?,
∴DBC 的长 =140π×6180=14π3.
【知识点】切线的性质、垂径定理、弧长的计算
26. 【答案】
(1) 连接 OD,
因为 OB=OD,
所以 ∠ABC=∠ODB,
因为 AB=AC,
所以 ∠ABC=∠ACB,
所以 ∠ODB=∠ACB,
所以 OD∥AC,
因为 DF 是 ⊙O 的切线,
所以 DF⊥OD,
所以 DF⊥AC.
(2) 连接 OE,
因为 DF⊥AC,∠CDF=22.5?,
所以 ∠ABC=∠ACB=67.5?,
所以 ∠BAC=45?,
因为 OA=OE,
所以 ∠AOE=90?,
因为 ⊙O 的半径为 4,
所以 S扇形AOE=4π,S△AOE=8,
所以 S阴影=4π?8.
【知识点】切线的性质、扇形面积的计算
(总分:120分 考试时间:120分钟)
一、选择题(36分)
(3分)在半径为 1 的圆中,弧长等于 2π3 的弧所对的圆心角是 ??
A. 30? B. 60? C. 120? D. 150?
(3分)如果 ⊙O 的半径为 3,扇形的面积为 3π,则扇形的圆心角度数是 ??
A. 150? B. 120? C. 60? D. 45?
(3分)如图,有一圆 O 通过 △ABC 的三个顶点.若 ∠B=75?,∠C=60?,且 BC 的长度为 4π,则 BC 的长度为 ??
A.8 B.82 C.16 D.162
(3分)如图,以 AB 为直径,点 O 为圆心的半圆经过点 C,若 AC=BC=2,则图中阴影部分的面积是 ??
A.π4 B.12+π4 C.π2 D.12+π2
(3分)半径为 6,圆心角为 120? 的扇形的面积是 ??
A.3π B.6π C.9π D.12π
(3分)如图,AB 是 ⊙O 的直径,AB=4,CD 是 ⊙O 的切线,切点为 D,CD 与 AB 的延长线交于点 C,若 ∠A=∠C,则 BD 的长为 ??
A. 13π B. 23π C. 43π D. 83π
(3分)如图,AB 是 ⊙O 的直径,CD⊥AB,∠ABD=60?,CD=23,则阴影部分的面积为 ??
A. 23π B. π C. 2π D. 4π
(3分)已知圆锥的底面半径为 3?cm,母线长为 4?cm,则圆锥的全面积是 ??
A. 15π?cm2 B. 21π?cm2 C. 20π?cm2 D. 24π?cm2
(3分)如图,已知点 C,D 是以 AB 为直径的半圆的三等分点,弧 CD 的长为 13π,则图中阴影部分的面积为 ??
A. 16π B. 316π C. 124π D. 112π+34
(3分)已知扇形的圆心角为 45?,半径长为 12,则该扇形的弧长为 ??
A. 3π4 B. 2π C. 3π D. 12π
(3分)一个扇形的圆心角是 120?,面积为 3π?cm2,那么这个扇形的半径是 ??
A.1?cm B.3?cm C.6?cm D.9?cm
(3分)如图,AB 是 ⊙O 的直径,M,N 是 AB(异于 A,B)上两点,C 是 MN 上一动点,∠ACB 的平分线交 ⊙O 于点 D,∠BAC 的平分线交 CD 于点 E.当点 C 从点 M 运动到点 N 时,则 C,E 两点的运动路径长的比是 ??
A. 2 B. π2 C. 32 D. 52
二、填空题(24分)
(3分)如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥底面圆的半径 r=2?cm,扇形的圆心角 θ=120?,则该圆锥的母线长 l 为 cm.
(3分)用半径为 30,圆心角为 120? 的扇形纸片围成一个圆锥的侧面,那么这个圆锥的底面圆半径是 .
(3分)如图,AB 是 ⊙O 的直径,点 C 在 ⊙O 上,连接 AC,BC,∠ACB 的平分线 CD 交 ⊙O 于点 D,若 ⊙O 的半径是 4,则 AD 的长是 .
(3分)如图,C 为 ⊙O 上一点,过点 C 的切线与直径 AB 的延长线交于点 D.若 AB=2,∠D=30?,则劣弧 AC 的长为 .
(3分)如图,半圆 O 的直径 AE=4,点 B,C,D 均在圆上,若 AB=BC,CD=DE,连接 OB,OD,则图中阴影部分的面积为 .
(3分)如图,矩形 ABCD 中,AB=2,BC=2,以 B 为圆心,BC 为半径画弧,交 AD 于点 E,则图中阴影部分的面积是 .
(3分)已知圆锥的底面半径是 2?cm,母线长为 3?cm,则圆锥的侧面积为 cm2.
(3分)要在三角形广场的三个角处各修一个半径为 2?m 的扇形草坪,则三个扇形弧长的和为 m.
三、解答题(60分)
(10分)如图,AB 为 ⊙O 的直径,点 C 在 ⊙O 上,过点 C 切线交 AB 的延长线上于 D,且已知 ∠A=22.5?.
(1) 求 ∠D 的度数;
(2) 若弦 CF⊥AB,垂足为 E,且 CF=2,求图中阴影部分的面积.
(10分)如图,在 △ABC 中,AB=AC,以 AB 为直径作 ⊙O,分别交 AC,BC 于点 D,E.
(1) 求证:BE=CE;
(2) 当 ∠BAC=40? 时,求 ∠ADE 的度数;
(3) 过点 E 作 ⊙O 的切线,交 AB 的延长线于点 F,当 AO=EF=2 时,求图中阴影部分的面积.
(10分)如图,△ABC 内接于 ⊙O,且 AB=AC,BD 是 ⊙O 的直径,AD 与 BC 交于点 E,F 在 DA 的延长线上,且 BF=BE.
(1) 试判断 BF 与 ⊙O 的位置关系,并说明理由;
(2) 若 BF=6,∠C=30?,求阴影的面积.
(10分)如图,以 AB 为直径的 ⊙O 经过 AC 的中点 D,DE⊥BC 于点 E.
(1) 求证:DE 是 ⊙O 的切线;
(2) 当 DE=1,∠C=30? 时,求图中阴影部分的面积.
(10分)如图,⊙O 的直径 AB 与弦 CD 相交于点 E,且 DE=CE,⊙O 的切线 BF 与弦 AD 的延长线交于点 F.
(1) 求证:CD∥BF;
(2) 若 ⊙O 的半径为 6,∠A=35?,求 DBC 的长.
(10分)如图,在 △ABC 中,AB=AC,以 AB 为直径的 ⊙O 分别与 BC,AC 交于点 D,E,过点 D 作 ⊙O 的切线 DF,交 AC 于点 F.
(1) 求证:DF⊥AC;
(2) 若 ⊙O 的半径为 4,∠CDF=22.5?,求阴影部分的面积.
答案
一、选择题(36分)
1. 【答案】C
【解析】设圆心角为 n?
∵1=nπr180,r=1,
∴nπ×1180=2π3,解得 n=120?.
【知识点】弧长的计算
2. 【答案】B
【解析】 S=nπr2360=nπ×9360=3π,
解得 n=120.
【知识点】扇形面积的计算
3. 【答案】B
【知识点】弧长的计算
4. 【答案】A
【解析】本题考查扇形面积的计算.∵AB 为直径,∴∠ACB=90?.
∵AC=BC=2,∴△ACB 为等腰直角三角形,∴OC⊥AB,∴△AOC 和 △BOC 都是等腰直角三角形,∴S△AOC=S△BOC,OA=22AC=1,∴S阴影部分=S扇形AOC=90×π×12360=π4.
【知识点】扇形面积的计算、圆周角定理及其推理
5. 【答案】D
【解析】根据扇形面积公式得 S=120360π×62=12π.
【知识点】扇形面积的计算
6. 【答案】B
【解析】如图,连接 OD,
∵CD 是 ⊙O 的切线,
∴OD⊥CD,
∴∠ODC=90?,
∴∠COD+∠C=90?,
∵∠A=∠C,∠COD=2∠A,
∴∠COD=2∠C,
∴3∠C=90?,
∴∠C=30?,
∴∠COD=2∠C=60?,
∵AB=4,
∴OB=2,
∴BD 的长为 60π×2180=23π.
【知识点】弧长的计算、切线的性质
7. 【答案】A
【解析】连接 OD.
∵CD⊥AB,
∴CE=DE=12CD=3,
故 S△OCE=S△ODE,即可得阴影部分的面积等于扇形 OBD 的面积,
又 ∵∠ABD=60?,
∴∠CDB=30?,
∴∠COB=60?,
∴OC=2,
∴S扇形OBD=60π×22360=2π3,即阴影部分的面积为 2π3.
【知识点】扇形面积的计算
8. 【答案】B
【解析】这个圆锥的底面圆的面积 =π?32=9π,
圆锥的侧面积 =12?2π?3?4=12π,
所以圆锥的全面积 =9π+12π=21πcm2.
【知识点】圆锥的计算
9. 【答案】A
【解析】连接 CD,OC,OD.
∵C,D 是以 AB 为直径的半圆周的三等分点,
∴∠AOC=∠COD=∠DOB=60?,AC=CD,
∵ 弧 CD 的长为 13π,
∴60π?r180=13π,解得:r=1,
又 ∵OA=OC=OD,
∴△OAC,△OCD 是等边三角形,
在 △OAC 和 △OCD 中,
OA=OC,OC=OD,AC=CD,
∴△OAC≌△OCDSSS,
∴S阴影=S扇形OCD=60π?12360=π6.
【知识点】扇形面积的计算
10. 【答案】C
【解析】根据弧长公式:l=45?π?12180=3π.
【知识点】弧长的计算
11. 【答案】B
【解析】设扇形的半径为 R,由题意:3π=120π?R2360,
解得 R=±3,
∵ R>0,
∴ R=3?cm,
∴ 这个扇形的半径为 3?cm.
【知识点】扇形面积的计算
12. 【答案】A
【解析】方法一:
如图,连接 EB.
设 OA=r.
∵AB 是直径,
∴∠ACB=90?,
∵E 是 △ACB 的内心,
∴∠AEB=135?,
∵∠ACD=∠BCD,
∴AD=DB,
∴AD=DB,
∴∠ADB=90?,
易知点 E 在以 D 为圆心 DA 为半径的圆上,运动轨迹是 GF,点 C 的运动轨迹是 MN,
∵∠MON=2∠GDF,设 ∠GDF=α,则 ∠MON=2α,
∴MNGF=2α?π?r180α?π?2r180=2.
方法二:
如图所示,连接 AD,BD,
∵ 点 E 是 ∠ACB 的平分线与 ∠BAC 的平分线的交点,
∴∠ACD=∠BCD,∠CAE=∠BAE.
∵∠BAD=∠BCD,
∴∠BAD+∠BAE=∠ACD+∠CAE,即 ∠DAE=∠AED,
∴AD=ED,
∴ 点 E 在以 D 为圆心,以 AD 为半径的圆上.
又 ∵AB 是 ⊙O 的直径,CD 是 ∠ACB 的平分线,
∴AD=BD,
∴AD=BD.
设 ⊙ 的半径为 r,
∴AD=2r,
∴ 点 E 的运动路径长是 90π?2r180=22πr.
∵ 点 C 是 MN 上一动点,
∴ 点 C 的运动路径长是 πr,
∴C,E 两点的运动路径长的比是 πr:22πr=2:1.
【知识点】弧长的计算
二、填空题(24分)
13. 【答案】6
【解析】根据题意,得 120πl180=2π×2,解得 l=6.
【知识点】圆锥的计算
14. 【答案】10
【解析】设圆锥底面圆的半径为 r,
则 2πr=120π×30180,
解得:r=10,
故圆锥的底面半径为 10.
【知识点】圆锥的计算
15. 【答案】 2π
【知识点】弧长的计算
16. 【答案】 23π
【知识点】弧长的计算、切线的性质
17. 【答案】π
【解析】连接 OC.
因为 AB=BC,CD=DE,
所以 AB=BC,CD=DE,
所以 ∠AOB=∠BOC,∠COD=∠DOE.
因为 ∠AOB+∠BOC+∠COD+∠DOE=180?,
所以 ∠AOB+∠DOE=90?.
因为直径 AE=4,
所以图中阴影部分的面积为 90?π?22360?=π.
【知识点】扇形面积的计算
18. 【答案】 22?1?π2
【解析】解:因为矩形 ABCD 中,AB=2,BC=2,
所以 AD=BC=2,CD=AB=2,∠A=90?,
因为 BE=BC=2,
在 Rt△ABE 中,AE=BE2?AB2=22?22=2,
所以 AB=AE,
所以 ∠ABE=∠EBC=45?,所以
S阴=S四边形BCDE?S扇形BEC=12×2+2?2×2?45?π?22360=22?1?π2,
故答案为 22?1?π2.
【知识点】扇形面积的计算
19. 【答案】 6π
【解析】底面半径是 2?cm,则底面周长 =4π?cm,圆锥的侧面积 =12×4π×3=6π?cm2.
【知识点】圆锥的计算
20. 【答案】 2π
【解析】设 △ABC 的三个内角的度数分别为 α,β,γ,
则 α+β+γ=180?,
三个扇形的弧长和为:
a×π×2180+β×π×2180+γ×π×2180=2π.
故答案为:2π.
【知识点】弧长的计算
三、解答题(60分)
21. 【答案】
(1) 略.
(2) 略.
【知识点】切线的性质、垂径定理、扇形面积的计算
22. 【答案】
(1) 连接 AE.
∵ AB 为 ⊙O 的直径,
∴ ∠AEB=90?,
∴ AE⊥BC.
∵ AB=AC,
∴ BE=CE.
(2) 由(1)得 ∠BAE=12×40?=20?,
∴ ∠ABE=70?,
∴ ∠ADE=∠EBF=180??70?=110?.
(3) 连接 OE.
∵ EF 切 ⊙O 于点 E,
∴ OE⊥EF.
∵ AO=EF=OE=2,
∴ ∠BOE=45?,
∴S阴影=S△OEF?S扇形OBE=12×2×2?45×π×22360=2?π2.
【知识点】扇形面积的计算、圆周角定理推论、切线的性质、圆内接四边形的性质
23. 【答案】
(1) BF 与 ⊙O 的位置关系是相切.
证明:
∵∠D 和 ∠C 都对弧 AB,
∴∠C=∠D.
∵BD 是直径,
∴∠DAB=90?.
∴∠D+∠ABD=90?.
∴∠C+∠ABD=90?.
∵∠DAB=90?,
∴BA⊥EF.
∵BE=BF,
∴∠EBA=∠FBA.
∵AB=AC,
∴∠C=∠EBA=∠FBA.
∵∠C+∠ABD=90?,
∴∠FBA+∠ABD=90?.
∴∠FBD=90?,
∵OB 是半径,
∴BF 是 ⊙O 的切线.
(2) 连接 OA.
∵∠C=∠D=30?=∠FBA,
∴ 在 Rt△ABF 中,BF=6,AF=BF=3.
由勾股定理得 AB=33.
在 Rt△DBA 中,∠D=30?,
∴BD=2AB=63,OB=33,∠BOA=2∠C=60?.
∵ 在 Rt△ABD 中,BD=63,AB=33,由勾股定理得:AD=9.
∵BO=OD,
∴S△BOA=S△AOD=12S△ABD=12×12×33×9=2734.
∴S阴影=S扇形OBA?S△OAB=60π×332360?2734=9π2?2734.
【知识点】扇形面积的计算、切线的判定
24. 【答案】
(1) 连接 OD.
∵AB 是 ⊙O 的直径,D 是 AC 的中点,
∴OD 是 △ABC 的中位线.
∴OD∥BC.
∵DE⊥BC,
∴OD⊥DE.
∵ 点 D 在圆上,
∴DE 为 ⊙O 的切线.
(2) ∵∠C=30?,DE=1,∠DEC=90?,
∴DC=2.
∵OD∥BC,
∴∠ODA=30?.
∵OD=OA,
∴∠OAD=∠ODA=30?,
∴∠AOD=120?,
∴OA=233,
∴ 阴影部分面积 S=120?π×2332360?12×2×33=4π9?33.
【知识点】扇形面积的计算、切线的判定
25. 【答案】
(1) 证明:∵AB 是 ⊙O 的直径,DE=CE,
∴AB⊥CD,
∵BF 是 ⊙O 的切线,
∴AB⊥BF,
∴CD∥BF;
(2) 连接 OD,OC,
∵∠A=35?,
∴BOD=2∠A=70?,
∴COD=2∠BOD=140?,
∴DBC 的长 =140π×6180=14π3.
【知识点】切线的性质、垂径定理、弧长的计算
26. 【答案】
(1) 连接 OD,
因为 OB=OD,
所以 ∠ABC=∠ODB,
因为 AB=AC,
所以 ∠ABC=∠ACB,
所以 ∠ODB=∠ACB,
所以 OD∥AC,
因为 DF 是 ⊙O 的切线,
所以 DF⊥OD,
所以 DF⊥AC.
(2) 连接 OE,
因为 DF⊥AC,∠CDF=22.5?,
所以 ∠ABC=∠ACB=67.5?,
所以 ∠BAC=45?,
因为 OA=OE,
所以 ∠AOE=90?,
因为 ⊙O 的半径为 4,
所以 S扇形AOE=4π,S△AOE=8,
所以 S阴影=4π?8.
【知识点】切线的性质、扇形面积的计算
同课章节目录
