六年级数学上册教学课件:第8单元 数学广角——数与形(共3课时55张ppt)人教版
文档属性
| 名称 | 六年级数学上册教学课件:第8单元 数学广角——数与形(共3课时55张ppt)人教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 19:31:57 | ||
图片预览




文档简介
运用数形结合发现规律
数学广角—数与形
8
先计算出结果,再说一说你发现了什么?
1+3=( )
4
1+3+5=( )
9
1+3+5+7=( )
16
1+3+5+7+9+…+21=( )
100
连续的奇数相加
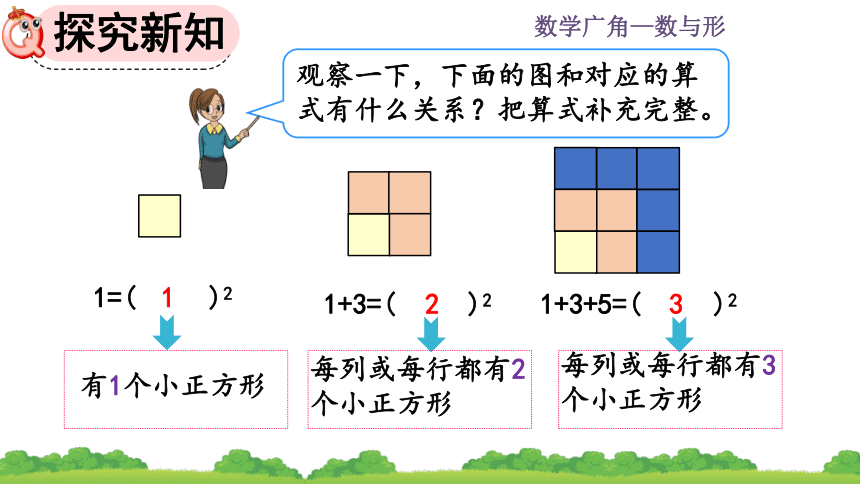
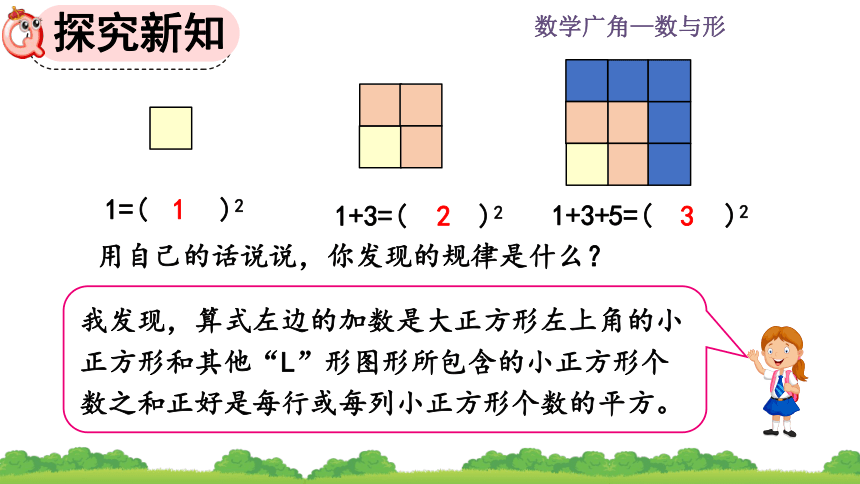
1=( )2
1+3=( )2
1+3+5=( )2
1
2
3
每列或每行都有2个小正方形
每列或每行都有3个小正方形
有1个小正方形
观察一下,下面的图和对应的算式有什么关系?把算式补充完整。
1=( )2
1+3=( )2
1
2
3
我发现,算式左边的加数是大正方形左上角的小正方形和其他“L”形图形所包含的小正方形个数之和正好是每行或每列小正方形个数的平方。
1+3+5=( )2
用自己的话说说,你发现的规律是什么?
1=( )2
1+3=( )2
1
2
3
1+3+5=( )2
我发现,从1开始的连续奇数的和正好是这串数个数的平方。
1
3
3
1
5
3
1
5
7
+
+
+
+
+
+
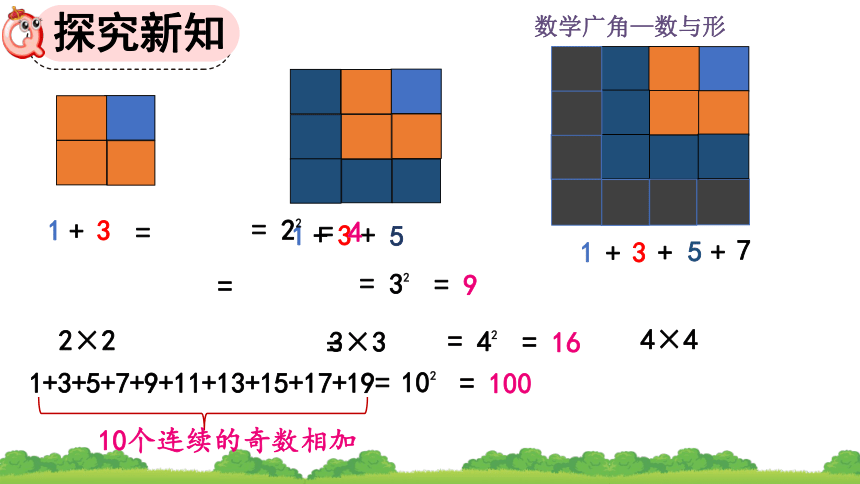
2×2
3×3
4×4
=
=
=
1+3+5+7+9+11+13+15+17+19=
10个连续的奇数相加
= 100
= 9
= 4
= 16
= 32
= 22
= 42
102
从1开始的连续奇数的和正好是这串数个数的平方。
每一个图形的个数正好等于从右上角加上其它L形图中所包含的个数。
图形
数形结合
算式
图形和算式有什么关系?
同桌交流:说一说你的发现,并用自己的语言解释规律。
只要是1开始,连续的奇数相加,就能排成每行、每列个数是几的大正方形,和也就是几的平方。
1+3+5+7=( )
1+3+5+7+9+11+13 =( )
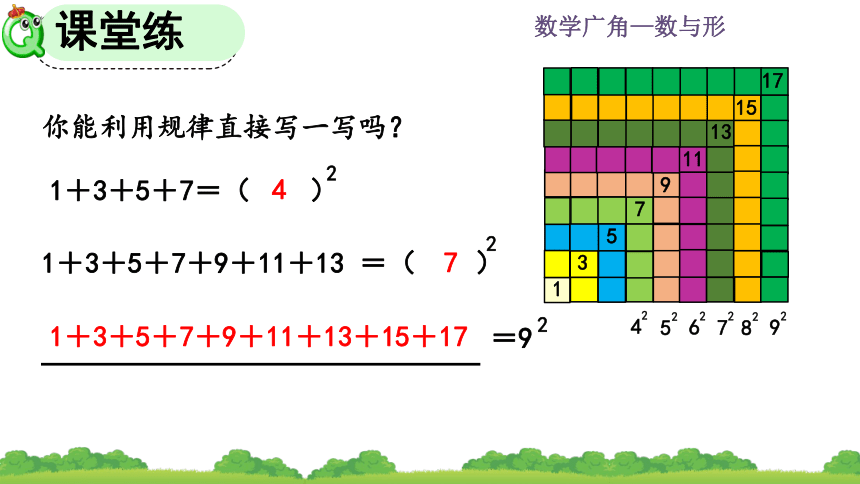
你能利用规律直接写一写吗?
4
7
1+3+5+7+9+11+13+15+17
=9
2
2
2
1
3
5
7
42
9
11
13
52
62
72
15
82
17
92
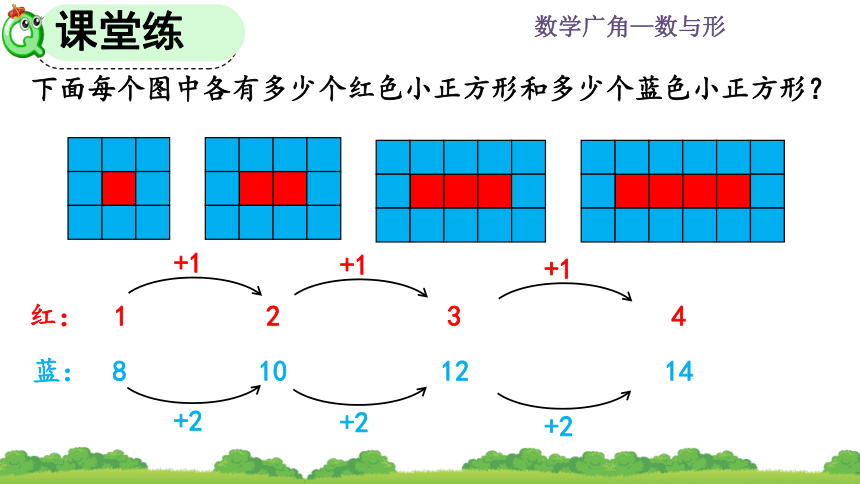
下面每个图中各有多少个红色小正方形和多少个蓝色小正方形?
红:
蓝:
1
8
2
10
3
12
4
14
+1
+2
+1
+2
+1
+2
红色正方形个数形成了1,2,3,4,…的数列,
蓝色正方形个数形成了8,10,12,14,…的数列。
中间每增加1个红色正方形,上下都必须增加2个蓝色正方形。
后一个图都比前一个图增加1个红色小正方形和2个蓝色小正方形。
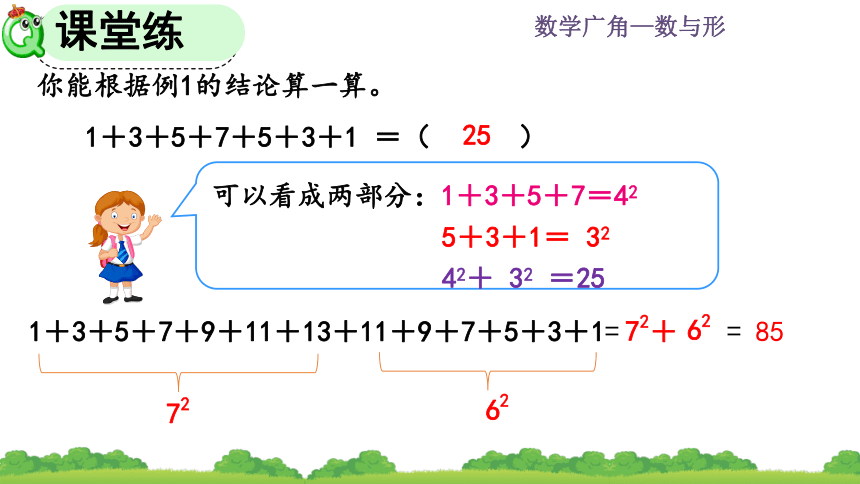
你能根据例1的结论算一算。
1+3+5+7+9+11+13+11+9+7+5+3+1=
+
= 85
1+3+5+7+5+3+1 =( )
25
可以看成两部分:1+3+5+7=42
5+3+1= 32
42+ 32 =25
72
62
72
62
下面每个图中最外圈有多少个小正方形?
照这样画下去,第5个图形最外圈有( )个小正方形。
40
3 -1= 8
2
5 -3 = 16
2
2
7 -5 = 24
2
2
11 -9 = 40
2
2
这节课你们都学会了哪些知识?
1.把图形与算式结合起来,是发现规律的关键。
2.从1开始的连续几个奇数的和与正方形数的关系,即有几个连续奇数相加,每边小正方形个数就是几的平方。
运用数形结合计算
数学广角—数与形
8
12+14=
?
12
?
14
?
18
?
116
?
12+14+18?=
?
算一算。
12+14=
?
34
?
12+14+18?=
?
78
?
?
12+14+18+116
?
=
12
?
14
?
18
?
116
?
12+14+18+116=
?
1516
?
你能发现什么规律?
每个算式从第二个数开始,每个数是前一个数的12?。
?
分子都是1
12+14=
?
34
?
12+14+18?=
?
78
?
12+14+18+116=1516
?
得数=1-最后一个加数
试着计算,看看刚才的结论对不对。
12+14+18+116+132+164?=
?
6364
?
12+14+18+116+132+164+…=
?
?
……
一个一个加下去,我发现,等号右边的分数越来越接近于1。
按顺序计算结果
12+14=
?
34
?
12+14+18?=
?
78
?
12+14+18+116=
?
1516
?
12+14+18+116+132+164?=
?
6364
?
画图探索规律
方法一
用一个圆表示“1”
12
?
12
?
14
?
12
?
14
?
18
?
12
?
12
?
+
14
?
=
+
18
?
12
?
+
14
?
=
画图探索规律
12
?
14
?
18
?
116
?
方法一
12
?
14
?
18
?
116
?
132
?
12
?
14
?
18
?
116
?
132
?
164
?
12
?
14
?
18
?
116
?
132
?
164
?
…
…
1
2
+
1
4
+
1
8
+
16
1
+
32
1
+
64
1
+
=
1
2
+
1
4
+
1
8
+
16
1
+
32
1
+
64
1
=
1
2
+
1
4
+
1
8
+
16
1
=
1
2
+
1
4
+
1
8
+
16
1
+
32
1
=
返回
2
1
4
1
16
1
8
1
…
32
1
8
7
4
3
16
15
32
31
64
63
128
127
从图上可以看出,这些分数不断加下去,总和就是1。
1
2
+
1
4
+
1
8
+
16
1
+
32
1
+
64
1
+
…
=1
1
2
+
=
1
4
3
4
1
2
1
4
3
4
3
4
+
=
1
8
7
8
7
8
1
8
7
8
+
=
16
1
16
15
16
1
32
1
16
15
32
1
16
15
+
=
32
31
32
31
64
63
128
127
…
…
绿色圃中小学教育网http://www.lspjy.com
绿色圃中小学教育网http://www.lspjy.com
绿色圃中小学教育网http://www.lspjy.com
方法二 用一条线段表示“1”
1
2
+
1
4
+
1
8
+
16
1
+
32
1
+
64
1
+
…
=
1
你能用所学知识解决下列问题吗?
1
2
3
+
=
2
9
8
9
8
9
+
=
27
2
27
26
81
2
27
26
+
=
81
80
……
2
3
2
27
2
9
2
81
…
+
+
+
+
=
所以原式的结果是1
找规律填空
2
2
2
2
2
2
4
2
( )
8
2
16
64
( )
2
8
16
从上到下外围数字都是2,内部数字都是它的左上角与右上角两个数字的积。
8×2=16
2×4=8
1
2
-
1
4
-
1
8
-
16
1
-
32
1
-
64
1
=
1
2
-
1
4
-
1
8
-
16
1
-
32
1
-
64
1
-
…
=
0
1-
64
1
1-
计算
用小棒按下面的方法摆图形
…
三角形个数:
小棒根数:
( )
( )
( )
( )
( )
( )
( )
( )
1
2
3
4
3
5
7
9
用小棒按下面的方法摆图形
…
(1)拼成的三角形的个数与所用的小棒根数之间有什么关系?
所用小棒根数等于三角形个数的2倍加1
三角形个数:
小棒根数:
( )
( )
( )
( )
( )
( )
( )
( )
1
2
3
4
3
5
7
9
用小棒按下面的方法摆图形
…
(2)第10个图形用了多少根小棒?
10×2+1=21(根)
答:第10个图形用了21根小棒。
所用小棒根数等于三角形个数的2倍加1
请将一根绳子沿中间对折,再沿对折的绳子中间再对折,这样连续对折5次,最后用剪刀沿对折5次后的绳子的中间将绳子剪断,此时绳子将被剪成多少段?
答:对折1次,将绳子中间剪断,绳子被剪成3段;对折2次,沿绳子中间剪断,绳子被剪成5段……依次类推,对折5次后,沿绳子中间剪断,绳子被剪成了33段。
这节课你们都学会了哪些知识?
数与形有着紧密的联系,在一定条件下可以相互转化。当用数形结合的方法解决问题时,使许多问题的解决变得很简单。
练习二十二
数学广角-数与形
8
数形结合思想是学习数学的一种重要
思想,运用数形结合的方法,探究数
学规律,可以使数学问题解决起来更
简单。
数与形
跟踪训练
照这样画下去,第50 个图形有( )个这样的小黑点。
2500
第几个图形,小黑点的个数就是几的平方,即第50个图形,就有2500个小黑点。
跟踪训练
看下列图形,把算式补充完整,再计算出后面算式的结果。
12
?
12
?
12
?
12+14=1?( )
?
12+14+18=1?(??????)
?
12+14+18+116=1?(??????)
?
14
?
=34
?
18
?
=78
?
116
?
=1516
?
14
?
14
?
14
?
18
?
18
?
116
?
12+14+18+116+…+1256=
?
255256
?
12+14=
?
34
?
12+14+18?=
?
78
?
得数=1-最后一个加数
请你根据上面图形与数的规律接着画一画,填一填。
15
21
28
如果不画,这样排列下去,第10个数是多少?
1+2+3+4……+10
=10×(10+1)÷2
=10×11÷2
=110÷2
=55
1
3
6
10
下面每个三角形都是由多少个小三角形组成的?如果小三角形的边长是1,每个三角形图的周长分别是多少?,每个三角形包含小三角形的个数与这个三角形图的周长之间有什么样的关系?
1
4
9
16
3
6
9
12
小三角形的个数=(周长÷3)?
三角形个数
周长
一条马路长200米,小亮和他的小狗分别以均匀的速度同时从马路的起点出发。当小亮走到这条马路一半的时候,小狗已到达马路的终点。然后小狗返回与小亮相向而行,遇到小亮以后再跑回终点,到达终点以后再与小亮相向而行……直到小亮到达终点。小狗从出发开始,一共跑了多少米?
由题意可知,小狗的速度等于小亮速度的2倍。
小狗的时间等于小亮走路的时间。
所以小狗跑的路程等于小亮走的路程的2倍。
答:小狗一共跑了400米。
起点
终点
200×2=400(米)
小兰和爸爸、妈妈一起步行到离家800m远的公园健身中心,用时20分钟。妈妈到了健身中心直接返回家里,还是用了20分钟。小兰和爸爸一起在健身中心锻炼了10分钟。然后,小兰跑步回到家中,用了5分钟,而爸爸是走回家中,用了15分钟。下面几个图哪个是描述妈妈离家时间和离家距离的关系?哪个是描述爸爸的?哪个是描述小兰的?
小兰
妈妈
爸爸
(1)求渔政船从港口出发赶往黄岩岛的速度。
150÷( 29?-8)=45(海里/时)
?
答:渔政船从港口出发赶往黄岩岛的速度是45海里/时。
黄岩岛是我国南沙群岛的一个小岛,渔产丰富。一天,某渔船离开港口前往这个海域捕鱼。捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并立即返航,渔政船接到报告后,立即从此港口出发赶往黄岩岛。渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的关系如图所示。(假设渔船与渔政船沿同一航线航行)
黄岩岛是我国南沙群岛的一个小岛,渔产丰富。一天,某渔船离开港口前往这个海域捕鱼。捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并立即返航,渔政船接到报告后,立即从此港口出发赶往黄岩岛。渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的关系如图所示。(假设渔船与渔政船沿同一航线航行)
(2)求渔船和渔政船相遇时,两船与黄岩岛的距离。
渔船的速度:150÷(13-8)=30(海里/时)
相遇时间:150÷(45+30)=2(小时)
两船与黄岩岛的距离:30×2=60(海里)
答:相遇时,两船与黄岩岛的距离是60海里。
答:小刚一共下了2盘,分别和小林、小强。
小刚
小林
小强
小芳
小兵
2
4
3
1
2
小林、小强、小芳、小兵和小刚5 人进行象棋 比赛,每2 人之间都要下一盘。小林已经下了4盘,小强下了3盘,小芳下了2 盘,小兵下了1 盘。请问:小刚一共下了几盘?分别和谁下的?
用连线的方法试试
我国宋代数学家杨辉在公元1261年撰写了《详解九章算法》,他在这本著作中画了一个由数构成的三角形图,我们把它称为“杨辉三角”。你能发现右面“杨辉三角”图中各数之间的关系吗?你能按照发现的规律把这个三角形表继续写下去吗?试试看。
1
6
15
20
15
6
1
都是1。
具有对称性(对称美),与首末两端“等距离 ”的两个数相等。
+
+
+
+
+
+
+
+
+
+
你能利用下面的图发现(a+b)? =a? +2ab +b?这一公式吗?利用你所学的面积计算的知识,探索一下。
大正方形的面积:
(a+b)?
(a+b)?
=a?+ab+ab+b?
=a?+2ab+b?
a
a
b
b
a?
ab
ab
b?
数形思想解决问题的方法:
把图形性质问题转化为数量关系问题或把数量关系问题转化为图形性质问题,可使复杂问题简单化,抽象问题具体化。
这节课你们都学会了哪些知识?
数学广角—数与形
8
先计算出结果,再说一说你发现了什么?
1+3=( )
4
1+3+5=( )
9
1+3+5+7=( )
16
1+3+5+7+9+…+21=( )
100
连续的奇数相加
1=( )2
1+3=( )2
1+3+5=( )2
1
2
3
每列或每行都有2个小正方形
每列或每行都有3个小正方形
有1个小正方形
观察一下,下面的图和对应的算式有什么关系?把算式补充完整。
1=( )2
1+3=( )2
1
2
3
我发现,算式左边的加数是大正方形左上角的小正方形和其他“L”形图形所包含的小正方形个数之和正好是每行或每列小正方形个数的平方。
1+3+5=( )2
用自己的话说说,你发现的规律是什么?
1=( )2
1+3=( )2
1
2
3
1+3+5=( )2
我发现,从1开始的连续奇数的和正好是这串数个数的平方。
1
3
3
1
5
3
1
5
7
+
+
+
+
+
+
2×2
3×3
4×4
=
=
=
1+3+5+7+9+11+13+15+17+19=
10个连续的奇数相加
= 100
= 9
= 4
= 16
= 32
= 22
= 42
102
从1开始的连续奇数的和正好是这串数个数的平方。
每一个图形的个数正好等于从右上角加上其它L形图中所包含的个数。
图形
数形结合
算式
图形和算式有什么关系?
同桌交流:说一说你的发现,并用自己的语言解释规律。
只要是1开始,连续的奇数相加,就能排成每行、每列个数是几的大正方形,和也就是几的平方。
1+3+5+7=( )
1+3+5+7+9+11+13 =( )
你能利用规律直接写一写吗?
4
7
1+3+5+7+9+11+13+15+17
=9
2
2
2
1
3
5
7
42
9
11
13
52
62
72
15
82
17
92
下面每个图中各有多少个红色小正方形和多少个蓝色小正方形?
红:
蓝:
1
8
2
10
3
12
4
14
+1
+2
+1
+2
+1
+2
红色正方形个数形成了1,2,3,4,…的数列,
蓝色正方形个数形成了8,10,12,14,…的数列。
中间每增加1个红色正方形,上下都必须增加2个蓝色正方形。
后一个图都比前一个图增加1个红色小正方形和2个蓝色小正方形。
你能根据例1的结论算一算。
1+3+5+7+9+11+13+11+9+7+5+3+1=
+
= 85
1+3+5+7+5+3+1 =( )
25
可以看成两部分:1+3+5+7=42
5+3+1= 32
42+ 32 =25
72
62
72
62
下面每个图中最外圈有多少个小正方形?
照这样画下去,第5个图形最外圈有( )个小正方形。
40
3 -1= 8
2
5 -3 = 16
2
2
7 -5 = 24
2
2
11 -9 = 40
2
2
这节课你们都学会了哪些知识?
1.把图形与算式结合起来,是发现规律的关键。
2.从1开始的连续几个奇数的和与正方形数的关系,即有几个连续奇数相加,每边小正方形个数就是几的平方。
运用数形结合计算
数学广角—数与形
8
12+14=
?
12
?
14
?
18
?
116
?
12+14+18?=
?
算一算。
12+14=
?
34
?
12+14+18?=
?
78
?
?
12+14+18+116
?
=
12
?
14
?
18
?
116
?
12+14+18+116=
?
1516
?
你能发现什么规律?
每个算式从第二个数开始,每个数是前一个数的12?。
?
分子都是1
12+14=
?
34
?
12+14+18?=
?
78
?
12+14+18+116=1516
?
得数=1-最后一个加数
试着计算,看看刚才的结论对不对。
12+14+18+116+132+164?=
?
6364
?
12+14+18+116+132+164+…=
?
?
……
一个一个加下去,我发现,等号右边的分数越来越接近于1。
按顺序计算结果
12+14=
?
34
?
12+14+18?=
?
78
?
12+14+18+116=
?
1516
?
12+14+18+116+132+164?=
?
6364
?
画图探索规律
方法一
用一个圆表示“1”
12
?
12
?
14
?
12
?
14
?
18
?
12
?
12
?
+
14
?
=
+
18
?
12
?
+
14
?
=
画图探索规律
12
?
14
?
18
?
116
?
方法一
12
?
14
?
18
?
116
?
132
?
12
?
14
?
18
?
116
?
132
?
164
?
12
?
14
?
18
?
116
?
132
?
164
?
…
…
1
2
+
1
4
+
1
8
+
16
1
+
32
1
+
64
1
+
=
1
2
+
1
4
+
1
8
+
16
1
+
32
1
+
64
1
=
1
2
+
1
4
+
1
8
+
16
1
=
1
2
+
1
4
+
1
8
+
16
1
+
32
1
=
返回
2
1
4
1
16
1
8
1
…
32
1
8
7
4
3
16
15
32
31
64
63
128
127
从图上可以看出,这些分数不断加下去,总和就是1。
1
2
+
1
4
+
1
8
+
16
1
+
32
1
+
64
1
+
…
=1
1
2
+
=
1
4
3
4
1
2
1
4
3
4
3
4
+
=
1
8
7
8
7
8
1
8
7
8
+
=
16
1
16
15
16
1
32
1
16
15
32
1
16
15
+
=
32
31
32
31
64
63
128
127
…
…
绿色圃中小学教育网http://www.lspjy.com
绿色圃中小学教育网http://www.lspjy.com
绿色圃中小学教育网http://www.lspjy.com
方法二 用一条线段表示“1”
1
2
+
1
4
+
1
8
+
16
1
+
32
1
+
64
1
+
…
=
1
你能用所学知识解决下列问题吗?
1
2
3
+
=
2
9
8
9
8
9
+
=
27
2
27
26
81
2
27
26
+
=
81
80
……
2
3
2
27
2
9
2
81
…
+
+
+
+
=
所以原式的结果是1
找规律填空
2
2
2
2
2
2
4
2
( )
8
2
16
64
( )
2
8
16
从上到下外围数字都是2,内部数字都是它的左上角与右上角两个数字的积。
8×2=16
2×4=8
1
2
-
1
4
-
1
8
-
16
1
-
32
1
-
64
1
=
1
2
-
1
4
-
1
8
-
16
1
-
32
1
-
64
1
-
…
=
0
1-
64
1
1-
计算
用小棒按下面的方法摆图形
…
三角形个数:
小棒根数:
( )
( )
( )
( )
( )
( )
( )
( )
1
2
3
4
3
5
7
9
用小棒按下面的方法摆图形
…
(1)拼成的三角形的个数与所用的小棒根数之间有什么关系?
所用小棒根数等于三角形个数的2倍加1
三角形个数:
小棒根数:
( )
( )
( )
( )
( )
( )
( )
( )
1
2
3
4
3
5
7
9
用小棒按下面的方法摆图形
…
(2)第10个图形用了多少根小棒?
10×2+1=21(根)
答:第10个图形用了21根小棒。
所用小棒根数等于三角形个数的2倍加1
请将一根绳子沿中间对折,再沿对折的绳子中间再对折,这样连续对折5次,最后用剪刀沿对折5次后的绳子的中间将绳子剪断,此时绳子将被剪成多少段?
答:对折1次,将绳子中间剪断,绳子被剪成3段;对折2次,沿绳子中间剪断,绳子被剪成5段……依次类推,对折5次后,沿绳子中间剪断,绳子被剪成了33段。
这节课你们都学会了哪些知识?
数与形有着紧密的联系,在一定条件下可以相互转化。当用数形结合的方法解决问题时,使许多问题的解决变得很简单。
练习二十二
数学广角-数与形
8
数形结合思想是学习数学的一种重要
思想,运用数形结合的方法,探究数
学规律,可以使数学问题解决起来更
简单。
数与形
跟踪训练
照这样画下去,第50 个图形有( )个这样的小黑点。
2500
第几个图形,小黑点的个数就是几的平方,即第50个图形,就有2500个小黑点。
跟踪训练
看下列图形,把算式补充完整,再计算出后面算式的结果。
12
?
12
?
12
?
12+14=1?( )
?
12+14+18=1?(??????)
?
12+14+18+116=1?(??????)
?
14
?
=34
?
18
?
=78
?
116
?
=1516
?
14
?
14
?
14
?
18
?
18
?
116
?
12+14+18+116+…+1256=
?
255256
?
12+14=
?
34
?
12+14+18?=
?
78
?
得数=1-最后一个加数
请你根据上面图形与数的规律接着画一画,填一填。
15
21
28
如果不画,这样排列下去,第10个数是多少?
1+2+3+4……+10
=10×(10+1)÷2
=10×11÷2
=110÷2
=55
1
3
6
10
下面每个三角形都是由多少个小三角形组成的?如果小三角形的边长是1,每个三角形图的周长分别是多少?,每个三角形包含小三角形的个数与这个三角形图的周长之间有什么样的关系?
1
4
9
16
3
6
9
12
小三角形的个数=(周长÷3)?
三角形个数
周长
一条马路长200米,小亮和他的小狗分别以均匀的速度同时从马路的起点出发。当小亮走到这条马路一半的时候,小狗已到达马路的终点。然后小狗返回与小亮相向而行,遇到小亮以后再跑回终点,到达终点以后再与小亮相向而行……直到小亮到达终点。小狗从出发开始,一共跑了多少米?
由题意可知,小狗的速度等于小亮速度的2倍。
小狗的时间等于小亮走路的时间。
所以小狗跑的路程等于小亮走的路程的2倍。
答:小狗一共跑了400米。
起点
终点
200×2=400(米)
小兰和爸爸、妈妈一起步行到离家800m远的公园健身中心,用时20分钟。妈妈到了健身中心直接返回家里,还是用了20分钟。小兰和爸爸一起在健身中心锻炼了10分钟。然后,小兰跑步回到家中,用了5分钟,而爸爸是走回家中,用了15分钟。下面几个图哪个是描述妈妈离家时间和离家距离的关系?哪个是描述爸爸的?哪个是描述小兰的?
小兰
妈妈
爸爸
(1)求渔政船从港口出发赶往黄岩岛的速度。
150÷( 29?-8)=45(海里/时)
?
答:渔政船从港口出发赶往黄岩岛的速度是45海里/时。
黄岩岛是我国南沙群岛的一个小岛,渔产丰富。一天,某渔船离开港口前往这个海域捕鱼。捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并立即返航,渔政船接到报告后,立即从此港口出发赶往黄岩岛。渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的关系如图所示。(假设渔船与渔政船沿同一航线航行)
黄岩岛是我国南沙群岛的一个小岛,渔产丰富。一天,某渔船离开港口前往这个海域捕鱼。捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并立即返航,渔政船接到报告后,立即从此港口出发赶往黄岩岛。渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的关系如图所示。(假设渔船与渔政船沿同一航线航行)
(2)求渔船和渔政船相遇时,两船与黄岩岛的距离。
渔船的速度:150÷(13-8)=30(海里/时)
相遇时间:150÷(45+30)=2(小时)
两船与黄岩岛的距离:30×2=60(海里)
答:相遇时,两船与黄岩岛的距离是60海里。
答:小刚一共下了2盘,分别和小林、小强。
小刚
小林
小强
小芳
小兵
2
4
3
1
2
小林、小强、小芳、小兵和小刚5 人进行象棋 比赛,每2 人之间都要下一盘。小林已经下了4盘,小强下了3盘,小芳下了2 盘,小兵下了1 盘。请问:小刚一共下了几盘?分别和谁下的?
用连线的方法试试
我国宋代数学家杨辉在公元1261年撰写了《详解九章算法》,他在这本著作中画了一个由数构成的三角形图,我们把它称为“杨辉三角”。你能发现右面“杨辉三角”图中各数之间的关系吗?你能按照发现的规律把这个三角形表继续写下去吗?试试看。
1
6
15
20
15
6
1
都是1。
具有对称性(对称美),与首末两端“等距离 ”的两个数相等。
+
+
+
+
+
+
+
+
+
+
你能利用下面的图发现(a+b)? =a? +2ab +b?这一公式吗?利用你所学的面积计算的知识,探索一下。
大正方形的面积:
(a+b)?
(a+b)?
=a?+ab+ab+b?
=a?+2ab+b?
a
a
b
b
a?
ab
ab
b?
数形思想解决问题的方法:
把图形性质问题转化为数量关系问题或把数量关系问题转化为图形性质问题,可使复杂问题简单化,抽象问题具体化。
这节课你们都学会了哪些知识?
