四年级数学上册课件 7.2 含有小括号的混合运算 苏教版(30张PPT)
文档属性
| 名称 | 四年级数学上册课件 7.2 含有小括号的混合运算 苏教版(30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 20:58:03 | ||
图片预览











文档简介
(共30张PPT)
第2课时
含有小括号的混合运算
整数四则混合运算
1.使学生掌握三步混合运算(含有小括号的)运算顺序,提高计算的正确率。
2.提高分析解决实际问题的能力,能根据一些常见的基本数量关系式进行分析、列式。
重点:体会小括号有改变原来运算顺序的作用,理解含有小括号的混合运算的运算顺序。??
教学目标
复习导入
一
12×3+15÷5
=36+3
=39
算式中加号两边的乘、除法可以同时计算,使计算过程简便。
在没有括号的算式里,有乘、除法和加、减法,要先算乘、除法,再算加、减法。若加法(或减法)两边同时又乘、除法,则乘、除法可以同时计算。
在计算不含括号的混合运算,同一级运算中,要按从左到右的顺序依次计算;不同级运算中,要先算乘、除法,后算加、减法。
100+120÷4×3
=100+30×3
=100+90
=190
新课探究
二
计算300?(120+25×4)。
算式里有括号,应该怎样算?
算式里有括号,先算括号里的。
探究点
含有小括号的混合运算
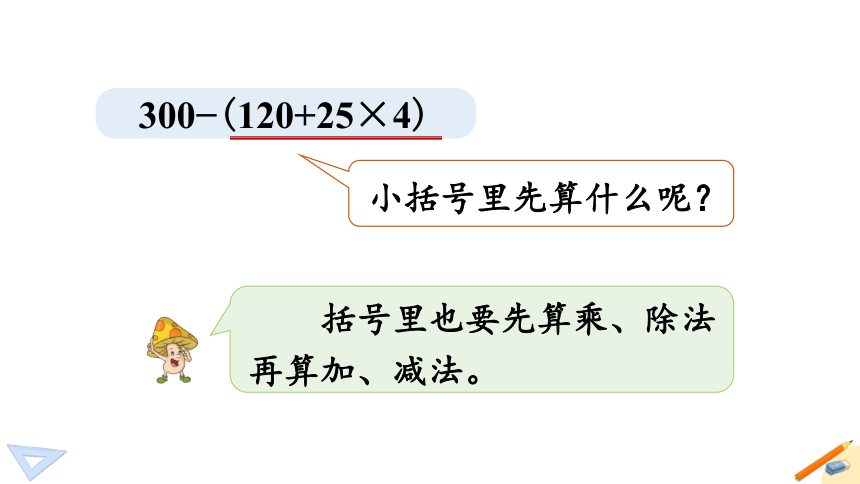
300?(120+25×4)
小括号里先算什么呢?
括号里也要先算乘、除法再算加、减法。
300?(120+25×4)
100
①
②
100+120
最后算小括号外面的减法
300?(120+25×4)
=300?(120+100)
=300?220
=80
先算出得数,再与同学交流。
括号里面也要先算乘、除法再算加、减法。
先算括号里面的。括号里算完了再算括号外的。
在进行四则混合运算时,有小括号的要先算小括号里面的,再算小括号外面的。如果在一个混合算式中含有两个或多个小括号,那么这几个小括号里面的部分可以同时进行,互不影响。
注意:括号里没有全部算完,括号不能去掉。
行程问题关系式的应用
知识延伸
甲、乙两辆汽车同时从A、B两地相向开出,甲车每小时行56千米,乙车每小时行48千米。两车在距中点32千米处相遇。A、B两地相距多少千米?
甲车比乙车多行了32×2=64(千米),可求出相遇时间
再根据“速度和×相遇时间=总路程
”求出A、B两地距离
经典例题
规范解答:
32×2÷(56-48)=8(小时)
(56+48)×8=832(千米)
答:A、B两地相距832千米。
1.一座大桥长2400米。一列火车以每分钟900米的速度通过大桥,从车头开上桥到车尾离开桥共需要3分钟。这列火车长多少米?
解火车过桥问题
应
用
1
速度×时间-桥长=车长
900×3-2400=300(米)
答:这列火车长300米。
2.一列火车,通过一座长720米的铁桥用了40秒,以同样的速度穿越长1220米的山洞用了60秒。求火车的速度及火车长。
根据山洞与铁桥的长度差和所用的时间差可求出火车的速度。
(1220-720)÷(60-40)=25(米/秒)
25×40-720=280(米)
答:火车的速度是25米/秒,火车长280米。
解相遇问题
应
用
2
3.快车和慢车同时从甲、乙两地相向开出,快车每小时行80千米,经过3小时,快车已驶过中点50千米,这时快车与慢车还相距14千米。慢车每小时行多少千米?
根据快车的速度和时间求得快车行驶的路程,已驶过中点50千米,求得到中点的距离是80×3-50=190(千米)
80×3-50=190(千米)
(190-50-14)÷3=42(千米)
答:慢车每小时行42千米。
求得慢车行驶的路程,已知行驶时间,可求出慢车速度
4.某地举行迎春长跑比赛,运动员跑到离起点3千米处要返回到起点。领先的运动员每分钟跑310米,最后的运动员每分钟跑290米。起跑后多少分钟这两个运动员相遇?相遇时离返回点多少米?
相遇时两个人的路程和是往返路程,根据
路程=速度×时间求出相遇时间和相遇位置
3千米=3000米
3000×2÷(310+290)=10(分钟)
3000-290×10=100(米)
答:起跑后10分钟这两个运动员相遇,相遇时离返回点100米。
解追及问题
应
用
3
5.一辆卡车的速度为每小时48千米,卡车开出1小时后,一辆小轿车以每小时72千米的速度从同一地点沿同一路线去追赶卡车。小轿车多少小时可追上卡车?追上时离出发地有多少千米?
追及时间=追及路程÷速度差
48×1÷(72-48)=2(小时)
72×2=144(千米)
答:小轿车2小时可追上卡车,
追上时离出发地有144千米。
6.甲、乙、丙三人速度分别是每小时4千米、5千米、8千米,都从A地到B地,甲出发2小时后乙从A地出发,恰好三人同时到达B地,乙出发几小时后丙才出发?
追及路程=追及时间×速度差,求出两地距离
4×2÷(5-4)=8(小时)
5×8=40(千米)
40÷8=5(小时)
8-5=3(小时)
答:乙出发3小时后丙才出发。
时间=路程÷速度,求出丙所用时间,和乙所用时间求差
教材习题
三
先说说运算顺序,再计算。
先算括号内的乘法,再算括号内的加法,最后算括号外的除法。
=(37+87)÷4
=124÷4
(37+29×3)÷4
=31
(37+29×3)÷4
先算括号内的除法,再算括号内的减法,最后算括号外的乘法。
=58×(20?6)
=58×14
58×(20?78÷3)
=812
58×(20?78÷3)
减
乘
加
172
除
减
乘
2090
小括号
乘、除
加、减
课堂练习
四
知
识
点
含有小括号的三步混合运算的运算顺序
二.计算下面各题。
(376+24)÷(23+27)
200+(50-42÷6)
?
?32-147÷(53-32)
=400÷50
=8
=200+(50-7)
=200+43
=243
=32-147÷21
=32-7=25
易错辨析
B
辨析:列综合算式解决问题时,漏写括号
=
>
>
<
<
培优训练
五
四则混合运算的综合应用
?
综合算式:(
)
(90+480÷12)×7=910
40
130
910
60×(50+40)÷2
60×(50+40÷2)
(60×50+40)÷2
1.在下列四个4中间添上适当的运算符号和括号,使等号左右两边相等。
4 4 4 4=0
4 4 4 4=1
4 4 4 4=2
4+4-4-4=0(答案不唯一)
4×4÷4÷4=1(答案不唯一)
4-(4+4)÷4=2(答案不唯一)
思维拓展
?
根据错误的计算顺序,用倒推的方法算出方框里的数是多少,然后将方框里的数代入正确的算式中,先算乘法,再算减法,最后算除法,从而得到正确的答案。
(90-78)×5÷3=20
(90-20×3)÷5=6
答:这道题的正确答案是6。
课堂小结
六
在一个算式里,有小括号的要先算小括号里面的,再算小括号外面的。小括号里面的算式要按照先乘除、后加减的顺序计算。
含有小括号的混合运算的顺序
第2课时
含有小括号的混合运算
整数四则混合运算
1.使学生掌握三步混合运算(含有小括号的)运算顺序,提高计算的正确率。
2.提高分析解决实际问题的能力,能根据一些常见的基本数量关系式进行分析、列式。
重点:体会小括号有改变原来运算顺序的作用,理解含有小括号的混合运算的运算顺序。??
教学目标
复习导入
一
12×3+15÷5
=36+3
=39
算式中加号两边的乘、除法可以同时计算,使计算过程简便。
在没有括号的算式里,有乘、除法和加、减法,要先算乘、除法,再算加、减法。若加法(或减法)两边同时又乘、除法,则乘、除法可以同时计算。
在计算不含括号的混合运算,同一级运算中,要按从左到右的顺序依次计算;不同级运算中,要先算乘、除法,后算加、减法。
100+120÷4×3
=100+30×3
=100+90
=190
新课探究
二
计算300?(120+25×4)。
算式里有括号,应该怎样算?
算式里有括号,先算括号里的。
探究点
含有小括号的混合运算
300?(120+25×4)
小括号里先算什么呢?
括号里也要先算乘、除法再算加、减法。
300?(120+25×4)
100
①
②
100+120
最后算小括号外面的减法
300?(120+25×4)
=300?(120+100)
=300?220
=80
先算出得数,再与同学交流。
括号里面也要先算乘、除法再算加、减法。
先算括号里面的。括号里算完了再算括号外的。
在进行四则混合运算时,有小括号的要先算小括号里面的,再算小括号外面的。如果在一个混合算式中含有两个或多个小括号,那么这几个小括号里面的部分可以同时进行,互不影响。
注意:括号里没有全部算完,括号不能去掉。
行程问题关系式的应用
知识延伸
甲、乙两辆汽车同时从A、B两地相向开出,甲车每小时行56千米,乙车每小时行48千米。两车在距中点32千米处相遇。A、B两地相距多少千米?
甲车比乙车多行了32×2=64(千米),可求出相遇时间
再根据“速度和×相遇时间=总路程
”求出A、B两地距离
经典例题
规范解答:
32×2÷(56-48)=8(小时)
(56+48)×8=832(千米)
答:A、B两地相距832千米。
1.一座大桥长2400米。一列火车以每分钟900米的速度通过大桥,从车头开上桥到车尾离开桥共需要3分钟。这列火车长多少米?
解火车过桥问题
应
用
1
速度×时间-桥长=车长
900×3-2400=300(米)
答:这列火车长300米。
2.一列火车,通过一座长720米的铁桥用了40秒,以同样的速度穿越长1220米的山洞用了60秒。求火车的速度及火车长。
根据山洞与铁桥的长度差和所用的时间差可求出火车的速度。
(1220-720)÷(60-40)=25(米/秒)
25×40-720=280(米)
答:火车的速度是25米/秒,火车长280米。
解相遇问题
应
用
2
3.快车和慢车同时从甲、乙两地相向开出,快车每小时行80千米,经过3小时,快车已驶过中点50千米,这时快车与慢车还相距14千米。慢车每小时行多少千米?
根据快车的速度和时间求得快车行驶的路程,已驶过中点50千米,求得到中点的距离是80×3-50=190(千米)
80×3-50=190(千米)
(190-50-14)÷3=42(千米)
答:慢车每小时行42千米。
求得慢车行驶的路程,已知行驶时间,可求出慢车速度
4.某地举行迎春长跑比赛,运动员跑到离起点3千米处要返回到起点。领先的运动员每分钟跑310米,最后的运动员每分钟跑290米。起跑后多少分钟这两个运动员相遇?相遇时离返回点多少米?
相遇时两个人的路程和是往返路程,根据
路程=速度×时间求出相遇时间和相遇位置
3千米=3000米
3000×2÷(310+290)=10(分钟)
3000-290×10=100(米)
答:起跑后10分钟这两个运动员相遇,相遇时离返回点100米。
解追及问题
应
用
3
5.一辆卡车的速度为每小时48千米,卡车开出1小时后,一辆小轿车以每小时72千米的速度从同一地点沿同一路线去追赶卡车。小轿车多少小时可追上卡车?追上时离出发地有多少千米?
追及时间=追及路程÷速度差
48×1÷(72-48)=2(小时)
72×2=144(千米)
答:小轿车2小时可追上卡车,
追上时离出发地有144千米。
6.甲、乙、丙三人速度分别是每小时4千米、5千米、8千米,都从A地到B地,甲出发2小时后乙从A地出发,恰好三人同时到达B地,乙出发几小时后丙才出发?
追及路程=追及时间×速度差,求出两地距离
4×2÷(5-4)=8(小时)
5×8=40(千米)
40÷8=5(小时)
8-5=3(小时)
答:乙出发3小时后丙才出发。
时间=路程÷速度,求出丙所用时间,和乙所用时间求差
教材习题
三
先说说运算顺序,再计算。
先算括号内的乘法,再算括号内的加法,最后算括号外的除法。
=(37+87)÷4
=124÷4
(37+29×3)÷4
=31
(37+29×3)÷4
先算括号内的除法,再算括号内的减法,最后算括号外的乘法。
=58×(20?6)
=58×14
58×(20?78÷3)
=812
58×(20?78÷3)
减
乘
加
172
除
减
乘
2090
小括号
乘、除
加、减
课堂练习
四
知
识
点
含有小括号的三步混合运算的运算顺序
二.计算下面各题。
(376+24)÷(23+27)
200+(50-42÷6)
?
?32-147÷(53-32)
=400÷50
=8
=200+(50-7)
=200+43
=243
=32-147÷21
=32-7=25
易错辨析
B
辨析:列综合算式解决问题时,漏写括号
=
>
>
<
<
培优训练
五
四则混合运算的综合应用
?
综合算式:(
)
(90+480÷12)×7=910
40
130
910
60×(50+40)÷2
60×(50+40÷2)
(60×50+40)÷2
1.在下列四个4中间添上适当的运算符号和括号,使等号左右两边相等。
4 4 4 4=0
4 4 4 4=1
4 4 4 4=2
4+4-4-4=0(答案不唯一)
4×4÷4÷4=1(答案不唯一)
4-(4+4)÷4=2(答案不唯一)
思维拓展
?
根据错误的计算顺序,用倒推的方法算出方框里的数是多少,然后将方框里的数代入正确的算式中,先算乘法,再算减法,最后算除法,从而得到正确的答案。
(90-78)×5÷3=20
(90-20×3)÷5=6
答:这道题的正确答案是6。
课堂小结
六
在一个算式里,有小括号的要先算小括号里面的,再算小括号外面的。小括号里面的算式要按照先乘除、后加减的顺序计算。
含有小括号的混合运算的顺序
