山东省济南外国语学校2012届高三5月份适应性训练(数学文)
文档属性
| 名称 | 山东省济南外国语学校2012届高三5月份适应性训练(数学文) |  | |
| 格式 | zip | ||
| 文件大小 | 128.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-25 15:00:06 | ||
图片预览



文档简介
绝密★启用前
济南外国语学校2012届高三5月适应性训练
文科数学试题
本试题卷共5页,共22题。满分150分。考试用时120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。用2B铅笔将答题卡上试卷类型A后的方框涂黑。
2.选择题的作答:每小题选出答案后,用统一提供的2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。答在试题卷、草稿纸上无效。
3.填空题和解答题的作答:用统一提供的签字笔直接答在答题卡上对应的答题区域内。答在试题卷、草稿纸上无效。
4.考生必须保持答题卡的整洁。考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如果复数的实部和虚部互为相反数,则的值等于( )
A.0 B.1 C.2 D.3
2.已知集合,则实数a的取值范围是
A.{1} B.(—,0)
C.d(1,+) D.(0,1)
3.某几何体的正视图与侧视图如图所示,若该几何体的体积为,则该几何体的俯视图可以是
4.函数(其中)的图象如图所示,为了得到的图象,则只需将的图象( )
A.向右平移个长度单位
B.向右平移个长度单位
C.向左平移个长度单位
D.向左平移个长度单位
5.给出下面的类比推理命题(其中Q为有理数集,R为实数集,C为复数集):
①“若a、b R,则a一b =0a =b”类比推出“a、b∈C,则a一b=0a=b”
②“若a、b、c、d∈R,则复数a+bi =c+dia=c,b=d"类比推出“若a、b、c、d∈Q,则“a
+b=c+da=c,b=d"
③“若a、bR,则a一ba >b"类比推出“a、b∈C,则a一b>0a>b”
④“若xR,则|x| <1一1其中类比结论正确的个数为
A.1 B.2 C.3 D.4
6.如图,D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点的仰角分别是,(<),则点A离地面的高度AB等于
7.一个样本容量为10的样本数据,它们组成一个公差不为O的等差数列{},若a3 =8,且a1,a3,a7成等比数列,则此样本的平均数和中位数分别是
A.13 ,12 B.13 ,13 C.12 ,13 D.13 ,14.
8.已知函数零点依次为a,b,c,则
A.b>c>a B.b>a>c C.a>b>c D.c>b>a
9.已知S,A,B,C是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=AB=l,BC=,则球O的表面积等于
A.4 B.3 C.2 D.
10.已知双曲线被斜率为的直线截得的弦的中点为,则该双曲线离心率的值为( )
A. B. C. D.
二、填空题:本大题共7小题,每小题5分,共35分. 请将答案填在答题卡对应题号的位置上. 答错位置,书写不清,模棱两可均不得分.
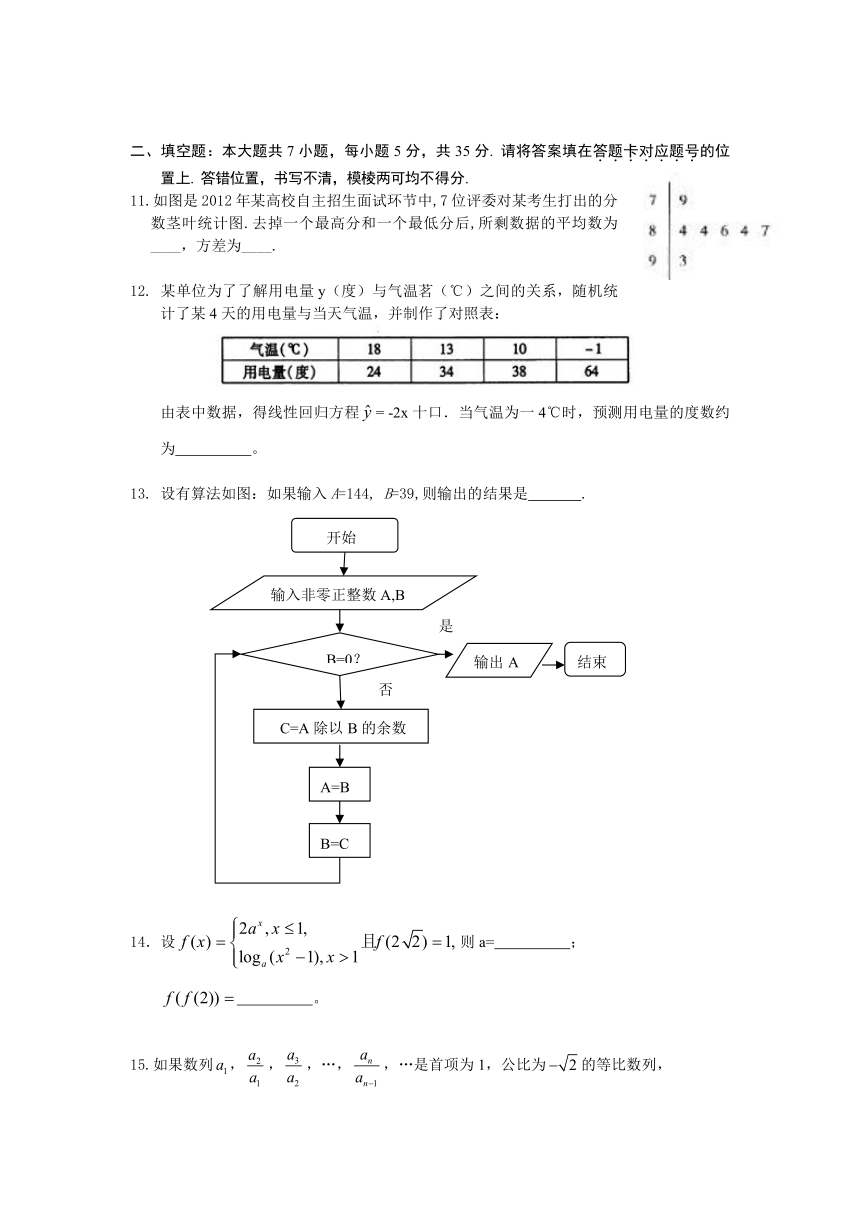
11.如图是2012年某高校自主招生面试环节中,7位评委对某考生打出的分 数茎叶统计图.去掉一个最高分和一个最低分后,所剩数据的平均数为____ ,方差为____ .
12. 某单位为了了解用电量y(度)与气温茗(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
由表中数据,得线性回归方程= -2x十口.当气温为一4℃时,预测用电量的度数约为 。
13. 设有算法如图:如果输入A=144, B=39,则输出的结果是 .
14.设则a= ;
。
15.如果数列,,,…,,…是首项为1,公比为的等比数列,
则等于
16.在平面直角坐标系中,为坐标原点,定义两点之间的“直角距离”为.已知,点为直线上的动点,则的最小值为 .
17.定义:为的真子集,,若,则称对加减法封闭。
有以下四个命题,请判断真假:
①自然数集对加减法封闭;②有理数集对加减法封闭;
③若有理数集对加减法封闭,则无理数集也对加减法封闭;
④若为的两个真子集,且对加减法封闭,则必存在,使得;
四个命题中为“真”的是 ;(填写序号)
三、解答题:本大题共5小题,共65分. 解答应写出文字说明、证明过程或演算步骤.
18.(本小题满分12分)
在△ABC中,角A、B、C的对边分别为a、b、c,已知B=60°,cos(B+C)=-.
(Ⅰ)求cosC的值;
(Ⅱ)若a=5,求△ABC的面积.
19.(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点.已知PD=,CD=4,AD=.
(Ⅰ)若∠ADE=,求证:CE⊥平面PDE;
(Ⅱ)当点A到平面PDE的距离为eq \f(2,7)时,求三棱锥A-PDE的侧面积.
20.(本小题满分13分)
某校为了解学生的视力情况,随机抽查了一部分学生的视力,将调查结果分组,分组区间为(3.9,4.2],(4.2,4.5],…,(5.1,5.4].经过数据处理,得到如下频率分布表:
分组 频数 频率
(3.9,4.2] 3 0.06
(4.2,4.5] 6 0.12
(4.5,4.8] 25 x
(4.8,5.1] y z
(5.1,5.4] 2 0.04
合计 n 1.00
(Ⅰ)求频率分布表中未知量n,x,y,z的值;
(Ⅱ)从样本中视力在(3.9,4.2]和(5.1,5.4]的所有同学中随机抽取两人,求两人的视力差的绝对值低于0.5的概率.
21.(本小题满分14分)
设a∈R,函数f(x)=lnx-ax.
(Ⅰ)讨论函数f(x)的单调区间和极值;
(Ⅱ)已知x1=(e为自然对数的底数)和x2是函数f(x)的两个不同的零点,求a的值并证明:x2>e.
22.(本小题满分14分)
已知椭圆Γ:+=1(a>b>0)的离心率为,半焦距为c(c>0),且a-c=1.经过椭圆的左焦点F,斜率为k1(k1≠0)的直线与椭圆交于A,B两点,O为坐标原点.
(Ⅰ)求椭圆Γ的标准方程;
(Ⅱ)当k1=1时,求S△AOB的值;
(Ⅲ)设R(1,0),延长AR,BR分别与椭圆交于C,D两点,直线CD的斜率为k2,求证:为定值.
文科数学试题参考答案及评分标准
一、选择题:每小题5分,满分50分.
1—5:ADDAB 6-10:ABADA
二、填空题:每小题5分,满分35分.
11.85 ,1.6 12. 68 13. 3 14. 7,6
15. 32 16.3 17.②④
三、解答题:本大题共5小题,共65分.
18.(本小题满分12分)
解:(Ⅰ)在△ABC中,由cos(B+C)=-,得
sin(B+C)==eq \r(,1-(-)2)=eq \f(5,14),
∴cosC=cos[(B+C)-B]=cos(B+C) cosB+sin(B+C) sinB
=-×+eq \f(5,14)×eq \f(,2)=.…………………………………………(6分)
(Ⅱ)由(Ⅰ),得sinC==eq \r(,1-()2)=eq \f(4,7),sinA=sin(B+C)=eq \f(5,14).
在△中,由正弦定理=,得
eq \f(5, eq \f(5,14))=eq \f(c,eq \f(4,7)),∴ c=8,
故△ABC的面积为S=acsinB=×5×8×eq \f(,2)=10.…………………(12分)
19.(本小题满分12分)
解:(Ⅰ)在Rt△DAE中,AD=,∠ADE=,
∴AE=AD·tan∠ADE=·eq \f(,3)=1.
又AB=CD=4,∴BE=3.
在Rt△EBC中,BC=AD=,∴tan∠CEB==eq \f(,3),∴∠CEB=.
又∠AED=,∴∠DEC=,即CE⊥DE.
∵PD⊥底面ABCD,CE底面ABCD,
∴PD⊥CE.
∴CE⊥平面PDE.……………………………………………………………(6分)
(Ⅱ)∵PD⊥底面ABCD,PD平面PDE,
∴平面PDE⊥平面ABCD.
如图,过A作AF⊥DE于F,∴AF⊥平面PDE,
∴AF就是点A到平面PDE的距离,即AF=eq \f(2,7).
在Rt△DAE中,由AD·AE=AF·DE,得
AE=eq \f(2,7)·,解得AE=2.
∴S△APD=PD·AD=××=eq \f(,2),
S△ADE=AD·AE=××2=,
∵BA⊥AD,BA⊥PD,∴BA⊥平面PAD,
∵PA平面PAD,∴BA⊥PA.
在Rt△PAE中,AE=2,PA===,
∴S△APE=PA·AE=××2=.
∴三棱锥A-PDE的侧面积S侧=eq \f(,2)++.…………………………(12分)
20.(本小题满分13分)
解:(Ⅰ)由频率分布表可知,样本容量为n,由=0.04,得n=50.
∴x==0.5,y=50-3-6-25-2=14,z===0.28.……………(6分)
(Ⅱ)记样本中视力在(3.9,4.2]的3人为a,b,c,在(5.1,5.4]的2人为d,e.
由题意,从5人中随机抽取两人,所有可能的结果有:{a,b},{a,c},{a,d},{a,e },{b,c},{b,d},{b,e },{c,d},{c,e },{d,e },共10种.
设事件A表示“两人的视力差的绝对值低于0.5”,则事件A包含的可能的结果有:{a,b},{a,c},{b,c},{d,e },共4种.
∴P(A)==.
故两人的视力差的绝对值低于0.5的概率为.…………………………(13分)
21.(本小题满分14分)
解:(Ⅰ)函数f(x)的定义域为(0,+∞).
求导数,得f ′(x)=-a=.
①若a≤0,则f ′(x)>0,f(x)是(0,+∞)上的增函数,无极值;
②若a>0,令f ′(x)=0,得x=.
当x∈(0,)时,f ′(x)>0,f(x)是增函数;
当x∈(,+∞)时,f ′(x)<0,f(x)是减函数.
∴当x=时,f(x)有极大值,极大值为f()=ln-1=-lna-1.
综上所述,当a≤0时,f(x)的递增区间为(0,+∞),无极值;当a>0时,f(x)的递增区间为(0,),递减区间为(,+∞),极大值为-lna-1.…(8分)
(Ⅱ)∵x1=是函数f(x)的零点,
∴f ()=0,即-a=0,解得a=eq \f(1,2)=eq \f(,2e).
∴f(x)=lnx-eq \f(1,2)x.
∵f(e)=->0,f(e)=-<0,∴f(e)f(e)<0.
由(Ⅰ)知,函数f(x)在(2,+∞)上单调递减,
∴函数f(x)在区间(e,e)上有唯一零点,
因此x2>e.………………………………………………………………(14分)
22.(本小题满分14分)
解:(Ⅰ)由题意,得eq \b\lc\{\rc\ (\a\vs4\al\co1(=,,a-c=1。))解得
∴b2=a2-c2=5,
故椭圆Γ的方程为+=1.………………………………………………(4分)
(Ⅱ)由(Ⅰ),知F(-2,0),∴直线AB的方程为y=x+2,
由eq \b\lc\{\rc\ (\a\vs4\al\co1(y=x+2,,+=1.))消去y并整理,得14x2+36x-9=0.
设A(x1,y1),B(x2,y2),则x1+x2=-,x1x2=-,
∴|AB|=| x1-x2|=·=.
设O点到直线AB的距离为d,则d=eq \f(|0-0+2|,)=.
∴S△AOB=|AB|·d=××=eq \f(15,7).…………………………………(8分)
(Ⅲ)设C(x3,y3),D(x4,y4),
由已知,直线AR的方程为y=(x-1),即x=y+1.
由eq \b\lc\{\rc\ (\a\vs4\al\co1(x=y+1,,+=1.))消去x并整理,得eq \f(5-x1,y)y 2+y-4=0.
则y1y3=-eq \f(4y,5-x1),∵y1≠0,∴y3=,
∴x3=y3+1=·+1=.
∴C(,).同理D(,).
∴k2=eq \f(-,-)=
=.
∵y1=k1(x1+2),y2=k1(x2+2),
∴k2===,
∴=为定值.……………………………………………………………(14分)
B=0?
C=A除以B的余数
A=B
B=C
输出A
输入非零正整数A,B
开始
结束
否
是
济南外国语学校2012届高三5月适应性训练
文科数学试题
本试题卷共5页,共22题。满分150分。考试用时120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。用2B铅笔将答题卡上试卷类型A后的方框涂黑。
2.选择题的作答:每小题选出答案后,用统一提供的2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。答在试题卷、草稿纸上无效。
3.填空题和解答题的作答:用统一提供的签字笔直接答在答题卡上对应的答题区域内。答在试题卷、草稿纸上无效。
4.考生必须保持答题卡的整洁。考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如果复数的实部和虚部互为相反数,则的值等于( )
A.0 B.1 C.2 D.3
2.已知集合,则实数a的取值范围是
A.{1} B.(—,0)
C.d(1,+) D.(0,1)
3.某几何体的正视图与侧视图如图所示,若该几何体的体积为,则该几何体的俯视图可以是
4.函数(其中)的图象如图所示,为了得到的图象,则只需将的图象( )
A.向右平移个长度单位
B.向右平移个长度单位
C.向左平移个长度单位
D.向左平移个长度单位
5.给出下面的类比推理命题(其中Q为有理数集,R为实数集,C为复数集):
①“若a、b R,则a一b =0a =b”类比推出“a、b∈C,则a一b=0a=b”
②“若a、b、c、d∈R,则复数a+bi =c+dia=c,b=d"类比推出“若a、b、c、d∈Q,则“a
+b=c+da=c,b=d"
③“若a、bR,则a一ba >b"类比推出“a、b∈C,则a一b>0a>b”
④“若xR,则|x| <1一1
A.1 B.2 C.3 D.4
6.如图,D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点的仰角分别是,(<),则点A离地面的高度AB等于
7.一个样本容量为10的样本数据,它们组成一个公差不为O的等差数列{},若a3 =8,且a1,a3,a7成等比数列,则此样本的平均数和中位数分别是
A.13 ,12 B.13 ,13 C.12 ,13 D.13 ,14.
8.已知函数零点依次为a,b,c,则
A.b>c>a B.b>a>c C.a>b>c D.c>b>a
9.已知S,A,B,C是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=AB=l,BC=,则球O的表面积等于
A.4 B.3 C.2 D.
10.已知双曲线被斜率为的直线截得的弦的中点为,则该双曲线离心率的值为( )
A. B. C. D.
二、填空题:本大题共7小题,每小题5分,共35分. 请将答案填在答题卡对应题号的位置上. 答错位置,书写不清,模棱两可均不得分.
11.如图是2012年某高校自主招生面试环节中,7位评委对某考生打出的分 数茎叶统计图.去掉一个最高分和一个最低分后,所剩数据的平均数为____ ,方差为____ .
12. 某单位为了了解用电量y(度)与气温茗(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
由表中数据,得线性回归方程= -2x十口.当气温为一4℃时,预测用电量的度数约为 。
13. 设有算法如图:如果输入A=144, B=39,则输出的结果是 .
14.设则a= ;
。
15.如果数列,,,…,,…是首项为1,公比为的等比数列,
则等于
16.在平面直角坐标系中,为坐标原点,定义两点之间的“直角距离”为.已知,点为直线上的动点,则的最小值为 .
17.定义:为的真子集,,若,则称对加减法封闭。
有以下四个命题,请判断真假:
①自然数集对加减法封闭;②有理数集对加减法封闭;
③若有理数集对加减法封闭,则无理数集也对加减法封闭;
④若为的两个真子集,且对加减法封闭,则必存在,使得;
四个命题中为“真”的是 ;(填写序号)
三、解答题:本大题共5小题,共65分. 解答应写出文字说明、证明过程或演算步骤.
18.(本小题满分12分)
在△ABC中,角A、B、C的对边分别为a、b、c,已知B=60°,cos(B+C)=-.
(Ⅰ)求cosC的值;
(Ⅱ)若a=5,求△ABC的面积.
19.(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点.已知PD=,CD=4,AD=.
(Ⅰ)若∠ADE=,求证:CE⊥平面PDE;
(Ⅱ)当点A到平面PDE的距离为eq \f(2,7)时,求三棱锥A-PDE的侧面积.
20.(本小题满分13分)
某校为了解学生的视力情况,随机抽查了一部分学生的视力,将调查结果分组,分组区间为(3.9,4.2],(4.2,4.5],…,(5.1,5.4].经过数据处理,得到如下频率分布表:
分组 频数 频率
(3.9,4.2] 3 0.06
(4.2,4.5] 6 0.12
(4.5,4.8] 25 x
(4.8,5.1] y z
(5.1,5.4] 2 0.04
合计 n 1.00
(Ⅰ)求频率分布表中未知量n,x,y,z的值;
(Ⅱ)从样本中视力在(3.9,4.2]和(5.1,5.4]的所有同学中随机抽取两人,求两人的视力差的绝对值低于0.5的概率.
21.(本小题满分14分)
设a∈R,函数f(x)=lnx-ax.
(Ⅰ)讨论函数f(x)的单调区间和极值;
(Ⅱ)已知x1=(e为自然对数的底数)和x2是函数f(x)的两个不同的零点,求a的值并证明:x2>e.
22.(本小题满分14分)
已知椭圆Γ:+=1(a>b>0)的离心率为,半焦距为c(c>0),且a-c=1.经过椭圆的左焦点F,斜率为k1(k1≠0)的直线与椭圆交于A,B两点,O为坐标原点.
(Ⅰ)求椭圆Γ的标准方程;
(Ⅱ)当k1=1时,求S△AOB的值;
(Ⅲ)设R(1,0),延长AR,BR分别与椭圆交于C,D两点,直线CD的斜率为k2,求证:为定值.
文科数学试题参考答案及评分标准
一、选择题:每小题5分,满分50分.
1—5:ADDAB 6-10:ABADA
二、填空题:每小题5分,满分35分.
11.85 ,1.6 12. 68 13. 3 14. 7,6
15. 32 16.3 17.②④
三、解答题:本大题共5小题,共65分.
18.(本小题满分12分)
解:(Ⅰ)在△ABC中,由cos(B+C)=-,得
sin(B+C)==eq \r(,1-(-)2)=eq \f(5,14),
∴cosC=cos[(B+C)-B]=cos(B+C) cosB+sin(B+C) sinB
=-×+eq \f(5,14)×eq \f(,2)=.…………………………………………(6分)
(Ⅱ)由(Ⅰ),得sinC==eq \r(,1-()2)=eq \f(4,7),sinA=sin(B+C)=eq \f(5,14).
在△中,由正弦定理=,得
eq \f(5, eq \f(5,14))=eq \f(c,eq \f(4,7)),∴ c=8,
故△ABC的面积为S=acsinB=×5×8×eq \f(,2)=10.…………………(12分)
19.(本小题满分12分)
解:(Ⅰ)在Rt△DAE中,AD=,∠ADE=,
∴AE=AD·tan∠ADE=·eq \f(,3)=1.
又AB=CD=4,∴BE=3.
在Rt△EBC中,BC=AD=,∴tan∠CEB==eq \f(,3),∴∠CEB=.
又∠AED=,∴∠DEC=,即CE⊥DE.
∵PD⊥底面ABCD,CE底面ABCD,
∴PD⊥CE.
∴CE⊥平面PDE.……………………………………………………………(6分)
(Ⅱ)∵PD⊥底面ABCD,PD平面PDE,
∴平面PDE⊥平面ABCD.
如图,过A作AF⊥DE于F,∴AF⊥平面PDE,
∴AF就是点A到平面PDE的距离,即AF=eq \f(2,7).
在Rt△DAE中,由AD·AE=AF·DE,得
AE=eq \f(2,7)·,解得AE=2.
∴S△APD=PD·AD=××=eq \f(,2),
S△ADE=AD·AE=××2=,
∵BA⊥AD,BA⊥PD,∴BA⊥平面PAD,
∵PA平面PAD,∴BA⊥PA.
在Rt△PAE中,AE=2,PA===,
∴S△APE=PA·AE=××2=.
∴三棱锥A-PDE的侧面积S侧=eq \f(,2)++.…………………………(12分)
20.(本小题满分13分)
解:(Ⅰ)由频率分布表可知,样本容量为n,由=0.04,得n=50.
∴x==0.5,y=50-3-6-25-2=14,z===0.28.……………(6分)
(Ⅱ)记样本中视力在(3.9,4.2]的3人为a,b,c,在(5.1,5.4]的2人为d,e.
由题意,从5人中随机抽取两人,所有可能的结果有:{a,b},{a,c},{a,d},{a,e },{b,c},{b,d},{b,e },{c,d},{c,e },{d,e },共10种.
设事件A表示“两人的视力差的绝对值低于0.5”,则事件A包含的可能的结果有:{a,b},{a,c},{b,c},{d,e },共4种.
∴P(A)==.
故两人的视力差的绝对值低于0.5的概率为.…………………………(13分)
21.(本小题满分14分)
解:(Ⅰ)函数f(x)的定义域为(0,+∞).
求导数,得f ′(x)=-a=.
①若a≤0,则f ′(x)>0,f(x)是(0,+∞)上的增函数,无极值;
②若a>0,令f ′(x)=0,得x=.
当x∈(0,)时,f ′(x)>0,f(x)是增函数;
当x∈(,+∞)时,f ′(x)<0,f(x)是减函数.
∴当x=时,f(x)有极大值,极大值为f()=ln-1=-lna-1.
综上所述,当a≤0时,f(x)的递增区间为(0,+∞),无极值;当a>0时,f(x)的递增区间为(0,),递减区间为(,+∞),极大值为-lna-1.…(8分)
(Ⅱ)∵x1=是函数f(x)的零点,
∴f ()=0,即-a=0,解得a=eq \f(1,2)=eq \f(,2e).
∴f(x)=lnx-eq \f(1,2)x.
∵f(e)=->0,f(e)=-<0,∴f(e)f(e)<0.
由(Ⅰ)知,函数f(x)在(2,+∞)上单调递减,
∴函数f(x)在区间(e,e)上有唯一零点,
因此x2>e.………………………………………………………………(14分)
22.(本小题满分14分)
解:(Ⅰ)由题意,得eq \b\lc\{\rc\ (\a\vs4\al\co1(=,,a-c=1。))解得
∴b2=a2-c2=5,
故椭圆Γ的方程为+=1.………………………………………………(4分)
(Ⅱ)由(Ⅰ),知F(-2,0),∴直线AB的方程为y=x+2,
由eq \b\lc\{\rc\ (\a\vs4\al\co1(y=x+2,,+=1.))消去y并整理,得14x2+36x-9=0.
设A(x1,y1),B(x2,y2),则x1+x2=-,x1x2=-,
∴|AB|=| x1-x2|=·=.
设O点到直线AB的距离为d,则d=eq \f(|0-0+2|,)=.
∴S△AOB=|AB|·d=××=eq \f(15,7).…………………………………(8分)
(Ⅲ)设C(x3,y3),D(x4,y4),
由已知,直线AR的方程为y=(x-1),即x=y+1.
由eq \b\lc\{\rc\ (\a\vs4\al\co1(x=y+1,,+=1.))消去x并整理,得eq \f(5-x1,y)y 2+y-4=0.
则y1y3=-eq \f(4y,5-x1),∵y1≠0,∴y3=,
∴x3=y3+1=·+1=.
∴C(,).同理D(,).
∴k2=eq \f(-,-)=
=.
∵y1=k1(x1+2),y2=k1(x2+2),
∴k2===,
∴=为定值.……………………………………………………………(14分)
B=0?
C=A除以B的余数
A=B
B=C
输出A
输入非零正整数A,B
开始
结束
否
是
同课章节目录
