2021-2022学年九年级数学北师大版上册《1.2矩形的性质与判定》同步优生辅导训练(word版含答案)
文档属性
| 名称 | 2021-2022学年九年级数学北师大版上册《1.2矩形的性质与判定》同步优生辅导训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 543.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 17:55:08 | ||
图片预览



文档简介
2021年北师大版九年级数学上册《1.2矩形的性质与判定》同步优生辅导训练(附答案)
1.如图,在?ABCD中,对角线AC、BD相交于点O,若再添加﹣个条件使?ABCD成为矩形,则该条件不可以是( )
A.AC=BD B.AO=BO C.∠BAD=90° D.∠AOB=90°
2.如图,矩形ABCD、△BDE中,A点在BE上.若矩形ABCD的面积为20,△BDE的面积为24,则△ADE的面积为何?( )
A.10 B.12 C.14 D.16
3.在平面直角坐标系中,已知四边形ABCD是矩形,点A(3,2),B(﹣3,2),C(﹣3,﹣2),则这个矩形的面积为( )
A.24 B.12 C.6 D.48
4.已知矩形的对角线为1,面积为m,则矩形的周长为( )
A. B. C.2 D.2
5.如图,在?ABCD中,BD⊥AD,AB=10,AD=6,作矩形DEBF,则其对角线EF的长为( )
A.8 B.9 C.10 D.11
6.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC:∠EDA=1:2,且AC=8,则EC的长度为( )
A.2 B.2 C.4 D.
7.如图,在矩形ABCD中放置了一个直角三角形EFG,点E在BC上,点F在AD上,∠EFG被AD平分,若∠CEF=35°,则∠EHF的度数为( )
A.55° B.125° C.130° D.135°
8.在矩形ABCD中,一条直线将矩形任意分为两部分,设这两部分图形的内角和分别为x、y,则x+y的和是( )
A.360°、540°、720° B.360°、540°
C.540°、720° D.360°、720°
9.如图,矩形ABCD中,AB=,四边形ABC1D1是平行四边形,点D1在BC边上且AD1=AD,△ABD1的面积是矩形ABCD面积的,则平行四边形ABC1D1的面积是( )
A.2 B.3 C.2 D.3
10.如图,在矩形ABCD中,AB=6,过对角线AC的中点O作EF⊥AC,分别交AB、DC于E、F,点G为AE的中点,若∠AOG=30°,则OG的长为( )
A.2 B.2 C. D.3
11.如图,矩形ABCD中,AB:AD=2:1,点E为AB的中点,点F为EC上一个动点,点P为DF的中点,连接PB.若PB的最小值为5,则AD的值为( )
A.5 B.6 C.7 D.8
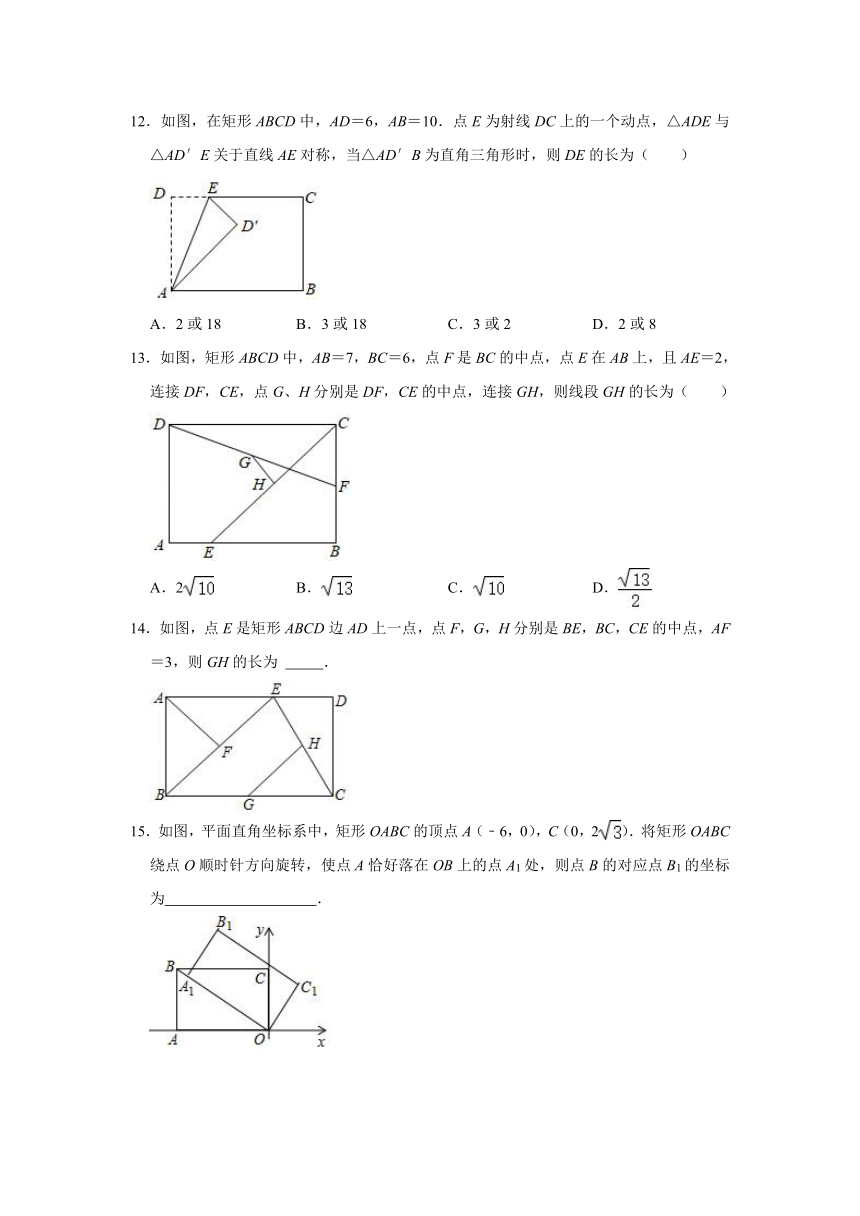
12.如图,在矩形ABCD中,AD=6,AB=10.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,则DE的长为( )
A.2或18 B.3或18 C.3或2 D.2或8
13.如图,矩形ABCD中,AB=7,BC=6,点F是BC的中点,点E在AB上,且AE=2,连接DF,CE,点G、H分别是DF,CE的中点,连接GH,则线段GH的长为( )
A.2 B. C. D.
14.如图,点E是矩形ABCD边AD上一点,点F,G,H分别是BE,BC,CE的中点,AF=3,则GH的长为 .
15.如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为 .
16.如图,矩形ABCD,∠BAC=60°,以点A为圆心,以任意长为半径作弧分别交AB,AC于点M,N两点,再分别以点M,N为圆心,以大于MN的长作半径作弧交于点P,作射线AP交BC于点E,若BE=1,则矩形ABCD的面积等于 .
17.如图,在矩形ABCD中,E是AB上一点,F是AD上一点,EF⊥FC,且EF=FC,已知DF=5cm,则AE的长为 cm.
18.如图,矩形ABCD中,AB=5,AD=12,点P在对角线BD上,且BP=BA,连接AP并延长,交DC的延长线于点Q,连接BQ,则BQ的长为 .
19.如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是40厘米,矩形的周长是22厘米,则对角线AC的长为 厘米.
20.如图,矩形ABCD的点A与坐标系的原点重合,边AB,AD分别落在x轴,y轴上(如图①所示),再将此矩形在坐标平面内绕原点逆时针旋转30°(如图②所示),若AB=4,BC=3,则图②中,点C的坐标为 .
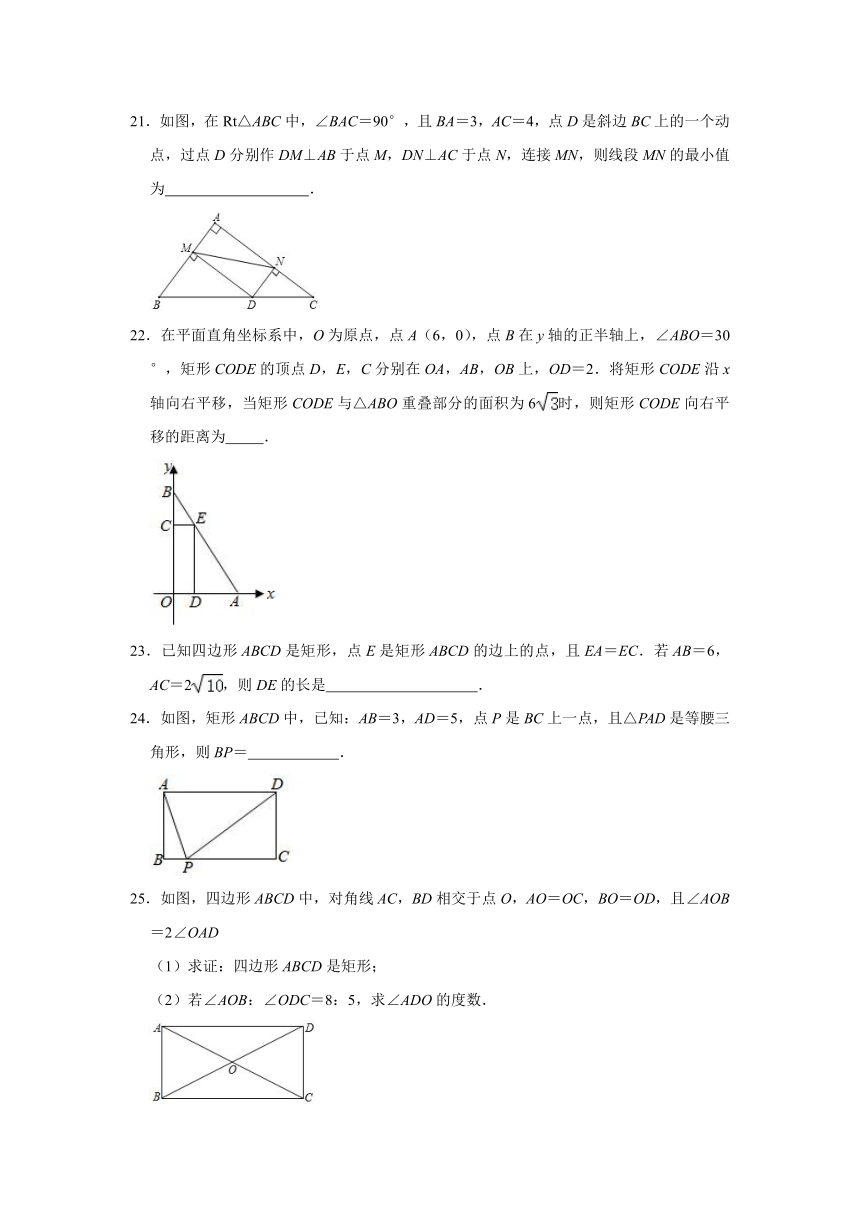
21.如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为 .
22.在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°,矩形CODE的顶点D,E,C分别在OA,AB,OB上,OD=2.将矩形CODE沿x轴向右平移,当矩形CODE与△ABO重叠部分的面积为6时,则矩形CODE向右平移的距离为 .
23.已知四边形ABCD是矩形,点E是矩形ABCD的边上的点,且EA=EC.若AB=6,AC=2,则DE的长是 .
24.如图,矩形ABCD中,已知:AB=3,AD=5,点P是BC上一点,且△PAD是等腰三角形,则BP= .
25.如图,四边形ABCD中,对角线AC,BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD
(1)求证:四边形ABCD是矩形;
(2)若∠AOB:∠ODC=8:5,求∠ADO的度数.
26.如图,在平行四边形ABCD中,点E,F分别是BC,AD的中点.
(1)求证:四边形AECF是平行四边形;
(2)当AB与AC满足什么数量关系时,四边形AECF是矩形?请证明.
27.如图,在平行四边形ABCD中,EF是直线DB上的两点,DE=BF.
(1)求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是矩形,且BD⊥AD,AB=5,AD=3,求DE的长.
28.如图,在平面直角坐标系中,A点坐标为(1,4),B点坐标为(1,1),将线段AB向右平移4个单位得到线段CD,若点P(m,m+1)在长方形ABCD的内部(包含边界).求m的取值范围.
29.在△ABC中,AB=AC,点D、O分别是边BC、AC的中点,连接AD,过点A作AE∥BC,交射线DO于点E,连接CE.
(1)如图1,求证:四边形ADCE是矩形;
(2)如图2,连接BE交AD于点F,连接OF,当∠ABC=60°时,在不添加任何字母和辅助线的情况下,请直接写出四条线段,长度分别是线段OF长度的4倍.
30.如图,已知长方形ABCO中,边AB=8,BC=4,以点O为原点OA,OC所在直线为y轴和轴建立直角坐标系.
(1)写出A,B,C三点的坐标;
(2)若点P从C点出发,以2个单位长度/秒的速度向CO方向移动(不超过点O),点Q从原点O出发,以1个单位长度/秒的速度向OA方向移动(不超过点A),设P,Q两点同时出发,在它们移动的过程中,四边形OPBQ的面积是否发生变化?若不变,求其值;若变化,请说明理由.
31.如图,在平行四边形ABCD中,点P是AB边上一点(不与A,B重合),过点P作PQ⊥CP,交AD边于点Q,且∠QPA=∠PCB,QP=QD.
(1)求证:四边形ABCD是矩形;
(2)求证:CD=CP.
32.如图1,已知AD∥BC,AB∥CD,∠B=∠C.
(1)求证:四边形ABCD为矩形;
(2)如图2,M为AD的中点,N为AB的中点,BN=2.若∠BNC=2∠DCM,求BC的长.
33.如图,在矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N.
(1)求证:△ABN≌△MAD;
(2)若AD=2,AN=4,求四边形BCMN的面积.
34.如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD,BC交于M,N两点,连接CM,AN.
(1)求证:四边形ANCM为平行四边形;
(2)若AD=4,AB=2,且MN⊥AC,求DM的长.
35.如图,在长方形ABCD中,AB=4cm,BC=6cm,点P从点B出发,以1cm/秒的速度沿BC向点C运动,点P到达C点时,运动停止.
(1)如图1,设点P的运动时间为t秒,则S△DCP= .(用代数式表示)
(2)如图2,当点P从点B开始运动的同时,点Q从点C出发,以vcm/秒的速度沿CD向点D运动,是否存在这样v的值,使得在某一时刻阴影部分的两个直角三角形全等?若存在,请求出v的值;若不存在,请说明理由.
36.《几何原本》中有一种证明勾股定理的方法:
如图,在Rt△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,分别以BC,AC,AB为边向外作正方形CBMN,正方形ACED,正方形ABHF,过点C作CG⊥FH,垂足为G,通过证明S正方形ACED=S矩形AFGP,S正方形BCNM=S矩形BHGP的方法来证明勾股定理.下面展示的是这种方法的不完整思路,请把内容补充完整.
证明:连接BD,CF,通过观察、推理,可以得到,△ADB≌ .
由AD∥CE得:
S正方形ACED与S△ADB的数量关系满足 ,
同理,可得,
S矩形AFGP与 的数量关系和S正方形ACED与S△ADB的数量关系相同,
∴S正方形ACED=S矩形AFGP即b2=S矩形AFGP.
同理,连接AM,CH,通过推理可得,a2= .
∴S正方形ACED+S正方形BCNM=S正方形ABHF.
∴a2+b2=c2.
参考答案
1.解:A、∵四边形ABCD是平行四边形,AC=BD,
∴平行四边形ABCD是矩形,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵AO=BO,
∴AC=BD,
∴平行四边形ABCD是矩形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,∠BAD=90°,
∴平行四边形ABCD是矩形,故选项C不符合题意;
D、∵∠AOB=90°,
∴AC⊥BD,
∵四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形,故选项D不符合题意;
故选:D.
2.解:∵四边形ABCD是矩形,
∴AB=CD,AD=CB.
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS).
∴S△ABD=S△CDB===10;
∵S△BED=S△ADE+S△ABD=24,
∴S△ADE=S△BDE﹣S△ABD=24﹣10=14.
故选:C.
3.解:如图,∵四边形ABCD是矩形,点A(3,2),B(﹣3,2),C(﹣3,﹣2),
∴AB=3+3=6,BC=2+2=4,
∴矩形ABCD的面积=AB×BC=6×4=24,
故选:A.
4.解:设矩形的长、宽分别为a、b,
∵矩形的对角线为1,面积为m,
∴a?+b?=1,ab=m,
∴a+b===,
∴矩形的周长为2(a+b)=2,
故选:C.
5.解:∵BD⊥AD,AB=10,AD=6,
∴DB=8,
∵矩形DEBF,
∴EF=DB=8,
故选:A.
6.解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD=8,OA=OC=AC=4,OB=OD=BD=4,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠EDC:∠EDA=1:2,∠EDC+∠EDA=90°,
∴∠EDC=30°,∠EDA=60°,
∵DE⊥AC,
∴∠DEC=90°,
∴∠DAC=30°,
∴DC=AC=4,
∴EC=DC=2,
故选:B.
7.解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFE=∠CEF=35°,
∵∠EFG被AD平分,
∴∠GFH=∠CEF=35°,
∵∠G=90°,
∴∠GHF=90°﹣35°=55°,
∴∠EHF=180°﹣55°=125°,
故选:B.
8.解:分三种情况:
①一条直线将矩形分为两个三角形,如图1所示:
则x+y=180°+180°=360°;
②一条直线将矩形分为一个三角形和一个四边形,如图2所示:
则x+y=180°+360°=540°;
③一条直线将矩形分为两个四边形,如图3所示:
则x+y=360°+360°=720°;
综上所述,x+y的和是360°或540°或720°,
故选:A.
9.解:∵点D1在BC边上,且△ABD1的面积是矩形ABCD面积的,
∴,
∴BD1=AD,
又∵AD1=AD,
∴BD1=AD1,
设BD1=2x,则AD1=3x,
在Rt△ABD1中,BD12+AB2=AD12,
∴(2x)2+()2=(3x)2,
解得:x=±1(负值舍去),
∴BD1=2,AD1=3,
∵点D1在BC边上,
∴平行四边形ABC1D1的面积=2S△ABD1=2×,
故选:C.
10.解:∵EF⊥AC,
∴∠AOE=90°,
在Rt△AOE中,G是AE的中点,
∴OG=AE=AG=GE,
∴∠OAG=∠AOG=30°,
∴∠OGE=60°,
∴△OGE是等边三角形,
设OG=x=OE,
∴AE=2x,AO=x,
∵O是AC的中点,
∴AC=2AO=x,
在Rt△ABC中,
BC=AC=x,
由勾股定理得,
AB2+BC2=AC2,
∴,
解得x=2.
∴OG=2,
故选:B.
11.解:当F运动时,P点轨迹为GH,如图,
,
∵AB:AD=2:1,
∴AD=AE=EB=BC,
∴∠ADE=∠DEA=∠CEB=∠ECB=45°,
∴∠DEC=90°,
BP的最距离为BP⊥GH时,此时P点与H点重合,F点与C点重合.
∵H为CD中点,
∴CH=CB,∠GHB=90°,
在Rt△HCB中,BH=5,
∴CH=CB=5,
故选:A.
12.解:分两种情况讨论:
①当E点在线段DC上时,如图所示:
∵△AD'E≌△ADE,
∴∠AD'E=∠D=90°,
∵∠AD'B=90°,
∴∠AD'B+∠AD'E=180°,
∴B、D'、E三点共线,
∵△ABE的面积=BE×AD'=AB×AD,AD'=AD,
∴BE=AB=10,
∵BD'===8,
∴DE=D'E=10﹣8=2;
②当E点在线段DC的延长线上,且ED″经过点B时,满足条件,如图所示:
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
,
∴△ABD″≌△BEC(ASA),
∴BE=AB=10,
∵BD''==8,
∴DE=D″E=BD''+BE=8+10=18;
综上所知,DE的长为2或18,
故选:A.
13.解:如图,连接CG并延长,交AD于M,连接ME,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DFC=∠FDM,
∵点F是BC的中点,点G是DF的中点,
∴CF=BC=3,DG=GF,
在△CGF和△MGD中,
,
∴△CGF≌△MGD(SAS),
∴DM=CF=3,CG=MG,
∴AM=3,
∴ME===,
∵CG=MG,点H是CE的中点,
∴GH=ME=,
故选:D.
14.解:在矩形ABCD中,∠BAD=90°,
∵F为BE的中点,AF=3,
∴BE=2AF=6.
∵G,H分别为BC,EC的中点,
∴GH=BE=3,
故答案为3.
15.解:连接OB1,作B1H⊥OA于H,
由题意得,OA=6,AB=OC=2,
∴∠BOA=30°,
∴∠OBA=60°,
由旋转的性质可知,∠B1OB=∠BOA=30°,
∴∠B1OH=60°,
在△AOB和△HB1O,
,
∴△AOB≌△HB1O,
∴B1H=OA=6,OH=AB=2,
∴点B1的坐标为(﹣2,6),
故答案为:(﹣2,6).
16.解:如图,∵四边形ABCD是矩形,
∴∠B=∠BAD=90°,
∵∠BAC=60°,
∴∠ACB=30°,
由作图知,AE是∠BAC的平分线,
∴∠BAE=∠CAE=30°,
∴∠EAC=∠ACE=30°,
∴AE=CE,
过E作EF⊥AC于F,
∴EF=BE=1,
∴AC=2CF=2,
∴AB=,BC=3,
∴矩形ABCD的面积=AB?BC=3,
故答案为:3.
17.解:∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∵EF⊥FC,
∴∠EFC=∠A=∠D=90°,
∴∠AFE+∠DFC=90°=∠DCF+∠DFC,
∴∠AFE=∠DCF,
在△AFE和△DCF中,
,
∴△AFE≌△DCF(AAS),
∴AE=DF=5cm,
故答案为5.
18.解:∵矩形ABCD中,AB=5,AD=12,∠BAD=∠BCD=90°,
∴BD==13,
∵BP=BA=5,
∴PD=BD﹣BP=8,
∵BA=BP,
∴∠BAP=∠BPA=∠DPQ,
∵AB∥CD,
∴∠BAP=∠DQP,
∴∠DPQ=∠DQP,
∴DQ=DP=8,
∴CQ=DQ﹣CD=DQ﹣AB=8﹣5=3,
∴在Rt△BCQ中,根据勾股定理,得
BQ===3.
故答案为:3.
19.解:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,AC=BF,AO=OC,OD=OB,
∴AO=OC=OD=OB,
∵矩形ABCD被两条对角线分成四个小三角形的周长的和是40厘米,
∴OA+OD+AD+OD+OC+CD+OC+OB+BC+OA+OB+AB=40厘米,
即8OA+2AB+2BC=40厘米,
∵矩形ABCD的周长是22厘米,
∴2AB+2BC=22厘米,
∴8OA=18厘米,
∴OA=2.25厘米,
即AC=BD=2OA=4.5厘米.
故答案为:4.5.
20.解:如图2,设CD与y轴交于点M,作CN⊥y轴于点N,
根据题意可知:∠DOM=30°,OD=3,
∴DM=3?tan30°=,OM=3÷cos30°=2,
∴CM=4﹣,
∵∠NCM=30°,
∴MN=,
则ON=OM+MN=,
∴图2中C点的坐标为(,).
故答案为:(,).
21.解:∵∠BAC=90°,且BA=3,AC=4,
∴BC==5,
∵DM⊥AB,DN⊥AC,
∴∠DMA=∠DNA=∠BAC=90°,
∴四边形DMAN是矩形,
∴MN=AD,
∴当AD⊥BC时,AD的值最小,
此时,△ABC的面积=AB×AC=BC×AD,
∴AD==,
∴MN的最小值为;
故答案为:.
22.解:∵点A(6,0),
∴OA=6,
∵OD=2,
∴AD=OA﹣OD=6﹣2=4,
∵四边形CODE是矩形,
∴DE∥OC,
∴∠AED=∠ABO=30°,
在Rt△AED中,AE=2AD=8,ED===4,
∵OD=2,
∴点E的坐标为(2,4);
∴矩形CODE的面积为4×2=8,
∵将矩形CODE沿x轴向右平移,矩形CODE与△ABO重叠部分的面积为6
∴矩形CODE与△ABO不重叠部分的面积为2,
如图,设ME′=x,则FE′=x,依题意有
x×x÷2=2,
解得x=±2(负值舍去).
故矩形CODE向右平移的距离为2.
故答案为:2.
23.解:如图,
∵四边形ABCD是矩形,
∴CD=AB=6,AD=BC,∠ABC=∠ADC=90°,
∴BC===2,
∴AD=2,
当点E在CD上时,
∵AE2=DE2+AD2=EC2,
∴(6﹣DE)2=DE2+4,
∴DE=;
当点E'在AB上时,
∵CE'2=BE'2+BC2=E'A2,
∴AE'2=(6﹣AE')2+4,
∴AE'=,
∴DE'===,
综上所述:DE=或,
故答案为:或.
24.解:①当DP=AD时,
∵矩形ABCD,
∴DC=AB=3,AD=BC=5,
∵△PAD是等腰三角形,
∴DP=AD=5,
在Rt△PCD中,
PC==4,
∴BP=BC﹣CP=5﹣4=1.
②当AD=AP时,
∴AP=AD=5,
在Rt△ABP中,
由勾股定理得,
BP==4,
③当AP=DP时,
过P作PE⊥AD于点E,
∴AE=AD=2.5,
∵∠B=∠BAE=∠AEP=90°,
∴四边形ABPE是矩形,
∴BP=AE=2.5.
综上所述,BP=1或4或2.5.
25.(1)证明:∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形,
∵∠AOB=∠DAO+∠ADO=2∠OAD,
∴∠DAO=∠ADO,
∴AO=DO,
∴AC=BD,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴AB∥CD,∠BAD=90°,
∴∠ABO=∠CDO,
∵∠AOB:∠ODC=8:5,
∴∠AOB:∠ABO=8:5,
∴∠BAO:∠AOB:∠ABO=5:8:5,
∴∠ABO=50°,
∵∠BAD=90°,
∴∠ADO=90°﹣50°=40°.
26.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵点E,F分别是BC,AD的中点.
∴AF=DF=AD,BE=CE=BC,
∴AF=CE,
∵AF∥EC,
∴四边形AECF是平行四边形;
(2)解:当AB=AC时,四边形AECF是矩形,证明如下:
由(1)得:四边形AECF是平行四边形,
∵AB=AC,
∴△ABC是等腰三角形,
∵点E是BC的中点,
∴AE⊥BC,
∴∠AEC=90°,
∴平行四边形AECF是矩形.
27.证明:(1)连接AC交EF于点O,
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵DE=BF,
∴OE=OF,
∴四边形AFCE是平行四边形;
(2)∵BD⊥AD,AB=5,AD=3,
∴BD===4,
∴BO=DO=2,
∴AO===,
∵四边形AFCE是矩形,
∴AO=CO,EO=FO,AC=EF,
∴AO=EO=,
∴DE=﹣2.
28.解:∵A点坐标为(1,4),B点坐标为(1,1),将线段AB向右平移4个单位得到线段CD,
∴四边形ABCD是矩形,
∴AB=3,BC=4,
由题意可得:,
解得:0≤m≤3,
点P(m,m+1)在直线y=x+1上,当1≤m≤3时,直线y=x+1落在长方形ABCD的内部(包含边界),
所以m的取值范围是1≤m≤3.
29.(1)证明:∵点D、O分别是边BC、AC的中点,
∴OD是△ABC的中位线,BD=CD,
∴OD∥AB,
∴DE∥AB,
∵AE∥BC,
∴四边形ABDE是平行四边形,
∴AE=BD=CD,
∴四边形ADCE是平行四边形,
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴∠ADC=90°,
∴平行四边形ADCE是矩形;
(2)解:长度分别是线段OF长度的4倍的线段为:AB、BC、AC、DE,理由如下:
∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC=BC,
由(1)得:四边形ABDE是平行四边形,四边形ADCE是矩形,
∴BF=EF,OD=OE,AC=DE,
∴OF是△BDE的中位线,
∴BD=2OF,
∵AB=AC=DE=BC=2BD,
∴AB=AC=DE=BC=4OF.
30.解:(1)∵四边形ABCO是矩形,
∴AB∥OC,AB=OC=8,AO=BC=4,BC∥AO,
∴点A(0,4),点B(8,4),点C(8,0);
(2)四边形OPBQ的面积不随t的增大而变化,理由如下:
设运动时间为t秒,则OQ=t,CP=2t,
∴AQ=4﹣t,
∴S△ABQ=×AB×AQ=×8×(4﹣t)=16﹣4t,
S△BCP=×PC×BC=×2t×4=4t,
∴S四边形OPBQ=S矩形ABCO﹣S△ABQ﹣S△BCP=32﹣(16﹣4t)﹣4t=16,
∴四边形OPBQ的面积不随t的增大而变化.
31.证明:(1)∵PQ⊥CP,
∴∠QPC=90°,
∴∠QPA+∠BPC=180°﹣90°=90°,
∵∠QPA=∠PCB,
∴∠BPC+∠PCB=90°,
∴∠B=180°﹣(∠BPC+∠PCB)=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形;
(2)连接CQ,
∵四边形ABCD是矩形,
∴∠D=90°,
∵∠CPQ=90°,
∴在Rt△CDQ和Rt△CPQ中
,
∴Rt△CDQ≌Rt△CPQ(HL),
∴CD=CP.
32.(1)证明:∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∵AB∥CD,
∴∠B+∠C=180°,
又∵∠B=∠C,
∴∠B=∠C=90°,
∴四边形ABCD为矩形;
(2)解:如图2,延长BA,CM交于点E,
∵M为AD的中点,N为AB中点,
∴AN=BN=2,AM=MD,
∴AB=CD=4,
∵AE∥DC,
∴∠E=∠DCM,
在△AEM和△DCM中,
,
∴△AME≌△DCM(AAS),
∴AE=CD=4,
∵∠BNC=2∠DCM=∠E+∠NCE,
∴∠NCE=∠DCM=∠E,
∴CN=EN=AE+AN=4+2=6,
∴BC===4.
33.(1)证明:在矩形ABCD中,∠D=90°,DC∥AB,
∴∠BAN=∠AMD,
∵BN⊥AM,
∴∠BNA=90°,
在△ABN和△MAD中,
,
∴△ABN≌△MAD(AAS);
(2)解:∵△ABN≌△MAD,
∴BN=AD,
∵AD=2,
∴BN=2,
又∵AN=4,
在Rt△ABN中,AB===2,
∴S矩形ABCD=2×2=4,S△ABN=S△MAD=×2×4=4,
∴S四边形BCMN=S矩形ABCD﹣S△ABN﹣S△MAD=4﹣8.
34.(1)证明:∵在矩形ABCD中,O为对角线AC的中点,
∴AD∥BC,AO=CO,
∴∠OAM=∠OCN,∠OMA=∠ONC,
在△AOM和△CON中,
,
∴△AOM≌△CON(AAS),
∴AM=CN,
∵AM∥CN,
∴四边形ANCM为平行四边形;
(2)解:∵在矩形ABCD中,AD=BC,
由(1)知:AM=CN,
∴DM=BN,
∵四边形ANCM为平行四边形,MN⊥AC,
∴平行四边形ANCM为菱形,
∴AM=AN=NC=AD﹣DM,
∴在Rt△ABN中,根据勾股定理,得
AN2=AB2+BN2,
∴(4﹣DM)2=22+DM2,
解得DM=.
35.解:(1)点P从点B出发,以1cm/秒的速度沿BC向点C运动,点P的运动时间为t秒时,BP=tcm,
则PC=(6﹣t)(cm);
∴S△DCP=CP?CD=(6﹣t)×4=(12﹣2t)(cm2),
故答案为(12﹣2t)cm2.
(2)①当BP=CQ,AB=PC时,△ABP≌△PCQ,
∵AB=4cm,
∴PC=4cm,
∴BP=6﹣4=2(cm),
即t=2,
∴CQ=BP=2cm,
∴v×2=2,
解得:v=1;
②当BA=CQ,PB=PC时,△ABP≌△QCP,
∵PB=PC,
∴BP=PC=BC=3,
即t=3,
∴CQ=BA=4cm,
∴v×3=4,
解得:v=.
综上所述:当v=或1时△ABP与△PQC全等.
36.证明:连接BD,CF,
∵四边形ADEC,四边形ABHF是正方形,
∴AB=AF,AD=AC,∠DAC=∠BAF,
∴∠DAB=∠CAF,
在△ADB和△ACF中,
,
∴△ADB≌△ACF(SAS).
∴S△ADB=S△ACF,
由AD∥CE得:S正方形ACED与S△ADB的数量关系满足S正方形ACED=2S△ADB,
同理可得,S矩形AFGP=2S△ACF,
∴S正方形ACED=S矩形AFGP,即b2=S矩形AFGP.
同理,连接AM,CH,通过推理可得,a2=S矩形BHGP.
∴S正方形ACED+S正方形BCNM=S正方形ABHF.
∴a2+b2=c2.
故答案为:△ACF,2S△ADB,S△ACF,S矩形BHGP.
1.如图,在?ABCD中,对角线AC、BD相交于点O,若再添加﹣个条件使?ABCD成为矩形,则该条件不可以是( )
A.AC=BD B.AO=BO C.∠BAD=90° D.∠AOB=90°
2.如图,矩形ABCD、△BDE中,A点在BE上.若矩形ABCD的面积为20,△BDE的面积为24,则△ADE的面积为何?( )
A.10 B.12 C.14 D.16
3.在平面直角坐标系中,已知四边形ABCD是矩形,点A(3,2),B(﹣3,2),C(﹣3,﹣2),则这个矩形的面积为( )
A.24 B.12 C.6 D.48
4.已知矩形的对角线为1,面积为m,则矩形的周长为( )
A. B. C.2 D.2
5.如图,在?ABCD中,BD⊥AD,AB=10,AD=6,作矩形DEBF,则其对角线EF的长为( )
A.8 B.9 C.10 D.11
6.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC:∠EDA=1:2,且AC=8,则EC的长度为( )
A.2 B.2 C.4 D.
7.如图,在矩形ABCD中放置了一个直角三角形EFG,点E在BC上,点F在AD上,∠EFG被AD平分,若∠CEF=35°,则∠EHF的度数为( )
A.55° B.125° C.130° D.135°
8.在矩形ABCD中,一条直线将矩形任意分为两部分,设这两部分图形的内角和分别为x、y,则x+y的和是( )
A.360°、540°、720° B.360°、540°
C.540°、720° D.360°、720°
9.如图,矩形ABCD中,AB=,四边形ABC1D1是平行四边形,点D1在BC边上且AD1=AD,△ABD1的面积是矩形ABCD面积的,则平行四边形ABC1D1的面积是( )
A.2 B.3 C.2 D.3
10.如图,在矩形ABCD中,AB=6,过对角线AC的中点O作EF⊥AC,分别交AB、DC于E、F,点G为AE的中点,若∠AOG=30°,则OG的长为( )
A.2 B.2 C. D.3
11.如图,矩形ABCD中,AB:AD=2:1,点E为AB的中点,点F为EC上一个动点,点P为DF的中点,连接PB.若PB的最小值为5,则AD的值为( )
A.5 B.6 C.7 D.8
12.如图,在矩形ABCD中,AD=6,AB=10.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,则DE的长为( )
A.2或18 B.3或18 C.3或2 D.2或8
13.如图,矩形ABCD中,AB=7,BC=6,点F是BC的中点,点E在AB上,且AE=2,连接DF,CE,点G、H分别是DF,CE的中点,连接GH,则线段GH的长为( )
A.2 B. C. D.
14.如图,点E是矩形ABCD边AD上一点,点F,G,H分别是BE,BC,CE的中点,AF=3,则GH的长为 .
15.如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为 .
16.如图,矩形ABCD,∠BAC=60°,以点A为圆心,以任意长为半径作弧分别交AB,AC于点M,N两点,再分别以点M,N为圆心,以大于MN的长作半径作弧交于点P,作射线AP交BC于点E,若BE=1,则矩形ABCD的面积等于 .
17.如图,在矩形ABCD中,E是AB上一点,F是AD上一点,EF⊥FC,且EF=FC,已知DF=5cm,则AE的长为 cm.
18.如图,矩形ABCD中,AB=5,AD=12,点P在对角线BD上,且BP=BA,连接AP并延长,交DC的延长线于点Q,连接BQ,则BQ的长为 .
19.如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是40厘米,矩形的周长是22厘米,则对角线AC的长为 厘米.
20.如图,矩形ABCD的点A与坐标系的原点重合,边AB,AD分别落在x轴,y轴上(如图①所示),再将此矩形在坐标平面内绕原点逆时针旋转30°(如图②所示),若AB=4,BC=3,则图②中,点C的坐标为 .
21.如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为 .
22.在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°,矩形CODE的顶点D,E,C分别在OA,AB,OB上,OD=2.将矩形CODE沿x轴向右平移,当矩形CODE与△ABO重叠部分的面积为6时,则矩形CODE向右平移的距离为 .
23.已知四边形ABCD是矩形,点E是矩形ABCD的边上的点,且EA=EC.若AB=6,AC=2,则DE的长是 .
24.如图,矩形ABCD中,已知:AB=3,AD=5,点P是BC上一点,且△PAD是等腰三角形,则BP= .
25.如图,四边形ABCD中,对角线AC,BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD
(1)求证:四边形ABCD是矩形;
(2)若∠AOB:∠ODC=8:5,求∠ADO的度数.
26.如图,在平行四边形ABCD中,点E,F分别是BC,AD的中点.
(1)求证:四边形AECF是平行四边形;
(2)当AB与AC满足什么数量关系时,四边形AECF是矩形?请证明.
27.如图,在平行四边形ABCD中,EF是直线DB上的两点,DE=BF.
(1)求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是矩形,且BD⊥AD,AB=5,AD=3,求DE的长.
28.如图,在平面直角坐标系中,A点坐标为(1,4),B点坐标为(1,1),将线段AB向右平移4个单位得到线段CD,若点P(m,m+1)在长方形ABCD的内部(包含边界).求m的取值范围.
29.在△ABC中,AB=AC,点D、O分别是边BC、AC的中点,连接AD,过点A作AE∥BC,交射线DO于点E,连接CE.
(1)如图1,求证:四边形ADCE是矩形;
(2)如图2,连接BE交AD于点F,连接OF,当∠ABC=60°时,在不添加任何字母和辅助线的情况下,请直接写出四条线段,长度分别是线段OF长度的4倍.
30.如图,已知长方形ABCO中,边AB=8,BC=4,以点O为原点OA,OC所在直线为y轴和轴建立直角坐标系.
(1)写出A,B,C三点的坐标;
(2)若点P从C点出发,以2个单位长度/秒的速度向CO方向移动(不超过点O),点Q从原点O出发,以1个单位长度/秒的速度向OA方向移动(不超过点A),设P,Q两点同时出发,在它们移动的过程中,四边形OPBQ的面积是否发生变化?若不变,求其值;若变化,请说明理由.
31.如图,在平行四边形ABCD中,点P是AB边上一点(不与A,B重合),过点P作PQ⊥CP,交AD边于点Q,且∠QPA=∠PCB,QP=QD.
(1)求证:四边形ABCD是矩形;
(2)求证:CD=CP.
32.如图1,已知AD∥BC,AB∥CD,∠B=∠C.
(1)求证:四边形ABCD为矩形;
(2)如图2,M为AD的中点,N为AB的中点,BN=2.若∠BNC=2∠DCM,求BC的长.
33.如图,在矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N.
(1)求证:△ABN≌△MAD;
(2)若AD=2,AN=4,求四边形BCMN的面积.
34.如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD,BC交于M,N两点,连接CM,AN.
(1)求证:四边形ANCM为平行四边形;
(2)若AD=4,AB=2,且MN⊥AC,求DM的长.
35.如图,在长方形ABCD中,AB=4cm,BC=6cm,点P从点B出发,以1cm/秒的速度沿BC向点C运动,点P到达C点时,运动停止.
(1)如图1,设点P的运动时间为t秒,则S△DCP= .(用代数式表示)
(2)如图2,当点P从点B开始运动的同时,点Q从点C出发,以vcm/秒的速度沿CD向点D运动,是否存在这样v的值,使得在某一时刻阴影部分的两个直角三角形全等?若存在,请求出v的值;若不存在,请说明理由.
36.《几何原本》中有一种证明勾股定理的方法:
如图,在Rt△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,分别以BC,AC,AB为边向外作正方形CBMN,正方形ACED,正方形ABHF,过点C作CG⊥FH,垂足为G,通过证明S正方形ACED=S矩形AFGP,S正方形BCNM=S矩形BHGP的方法来证明勾股定理.下面展示的是这种方法的不完整思路,请把内容补充完整.
证明:连接BD,CF,通过观察、推理,可以得到,△ADB≌ .
由AD∥CE得:
S正方形ACED与S△ADB的数量关系满足 ,
同理,可得,
S矩形AFGP与 的数量关系和S正方形ACED与S△ADB的数量关系相同,
∴S正方形ACED=S矩形AFGP即b2=S矩形AFGP.
同理,连接AM,CH,通过推理可得,a2= .
∴S正方形ACED+S正方形BCNM=S正方形ABHF.
∴a2+b2=c2.
参考答案
1.解:A、∵四边形ABCD是平行四边形,AC=BD,
∴平行四边形ABCD是矩形,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵AO=BO,
∴AC=BD,
∴平行四边形ABCD是矩形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,∠BAD=90°,
∴平行四边形ABCD是矩形,故选项C不符合题意;
D、∵∠AOB=90°,
∴AC⊥BD,
∵四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形,故选项D不符合题意;
故选:D.
2.解:∵四边形ABCD是矩形,
∴AB=CD,AD=CB.
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS).
∴S△ABD=S△CDB===10;
∵S△BED=S△ADE+S△ABD=24,
∴S△ADE=S△BDE﹣S△ABD=24﹣10=14.
故选:C.
3.解:如图,∵四边形ABCD是矩形,点A(3,2),B(﹣3,2),C(﹣3,﹣2),
∴AB=3+3=6,BC=2+2=4,
∴矩形ABCD的面积=AB×BC=6×4=24,
故选:A.
4.解:设矩形的长、宽分别为a、b,
∵矩形的对角线为1,面积为m,
∴a?+b?=1,ab=m,
∴a+b===,
∴矩形的周长为2(a+b)=2,
故选:C.
5.解:∵BD⊥AD,AB=10,AD=6,
∴DB=8,
∵矩形DEBF,
∴EF=DB=8,
故选:A.
6.解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD=8,OA=OC=AC=4,OB=OD=BD=4,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠EDC:∠EDA=1:2,∠EDC+∠EDA=90°,
∴∠EDC=30°,∠EDA=60°,
∵DE⊥AC,
∴∠DEC=90°,
∴∠DAC=30°,
∴DC=AC=4,
∴EC=DC=2,
故选:B.
7.解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFE=∠CEF=35°,
∵∠EFG被AD平分,
∴∠GFH=∠CEF=35°,
∵∠G=90°,
∴∠GHF=90°﹣35°=55°,
∴∠EHF=180°﹣55°=125°,
故选:B.
8.解:分三种情况:
①一条直线将矩形分为两个三角形,如图1所示:
则x+y=180°+180°=360°;
②一条直线将矩形分为一个三角形和一个四边形,如图2所示:
则x+y=180°+360°=540°;
③一条直线将矩形分为两个四边形,如图3所示:
则x+y=360°+360°=720°;
综上所述,x+y的和是360°或540°或720°,
故选:A.
9.解:∵点D1在BC边上,且△ABD1的面积是矩形ABCD面积的,
∴,
∴BD1=AD,
又∵AD1=AD,
∴BD1=AD1,
设BD1=2x,则AD1=3x,
在Rt△ABD1中,BD12+AB2=AD12,
∴(2x)2+()2=(3x)2,
解得:x=±1(负值舍去),
∴BD1=2,AD1=3,
∵点D1在BC边上,
∴平行四边形ABC1D1的面积=2S△ABD1=2×,
故选:C.
10.解:∵EF⊥AC,
∴∠AOE=90°,
在Rt△AOE中,G是AE的中点,
∴OG=AE=AG=GE,
∴∠OAG=∠AOG=30°,
∴∠OGE=60°,
∴△OGE是等边三角形,
设OG=x=OE,
∴AE=2x,AO=x,
∵O是AC的中点,
∴AC=2AO=x,
在Rt△ABC中,
BC=AC=x,
由勾股定理得,
AB2+BC2=AC2,
∴,
解得x=2.
∴OG=2,
故选:B.
11.解:当F运动时,P点轨迹为GH,如图,
,
∵AB:AD=2:1,
∴AD=AE=EB=BC,
∴∠ADE=∠DEA=∠CEB=∠ECB=45°,
∴∠DEC=90°,
BP的最距离为BP⊥GH时,此时P点与H点重合,F点与C点重合.
∵H为CD中点,
∴CH=CB,∠GHB=90°,
在Rt△HCB中,BH=5,
∴CH=CB=5,
故选:A.
12.解:分两种情况讨论:
①当E点在线段DC上时,如图所示:
∵△AD'E≌△ADE,
∴∠AD'E=∠D=90°,
∵∠AD'B=90°,
∴∠AD'B+∠AD'E=180°,
∴B、D'、E三点共线,
∵△ABE的面积=BE×AD'=AB×AD,AD'=AD,
∴BE=AB=10,
∵BD'===8,
∴DE=D'E=10﹣8=2;
②当E点在线段DC的延长线上,且ED″经过点B时,满足条件,如图所示:
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
,
∴△ABD″≌△BEC(ASA),
∴BE=AB=10,
∵BD''==8,
∴DE=D″E=BD''+BE=8+10=18;
综上所知,DE的长为2或18,
故选:A.
13.解:如图,连接CG并延长,交AD于M,连接ME,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DFC=∠FDM,
∵点F是BC的中点,点G是DF的中点,
∴CF=BC=3,DG=GF,
在△CGF和△MGD中,
,
∴△CGF≌△MGD(SAS),
∴DM=CF=3,CG=MG,
∴AM=3,
∴ME===,
∵CG=MG,点H是CE的中点,
∴GH=ME=,
故选:D.
14.解:在矩形ABCD中,∠BAD=90°,
∵F为BE的中点,AF=3,
∴BE=2AF=6.
∵G,H分别为BC,EC的中点,
∴GH=BE=3,
故答案为3.
15.解:连接OB1,作B1H⊥OA于H,
由题意得,OA=6,AB=OC=2,
∴∠BOA=30°,
∴∠OBA=60°,
由旋转的性质可知,∠B1OB=∠BOA=30°,
∴∠B1OH=60°,
在△AOB和△HB1O,
,
∴△AOB≌△HB1O,
∴B1H=OA=6,OH=AB=2,
∴点B1的坐标为(﹣2,6),
故答案为:(﹣2,6).
16.解:如图,∵四边形ABCD是矩形,
∴∠B=∠BAD=90°,
∵∠BAC=60°,
∴∠ACB=30°,
由作图知,AE是∠BAC的平分线,
∴∠BAE=∠CAE=30°,
∴∠EAC=∠ACE=30°,
∴AE=CE,
过E作EF⊥AC于F,
∴EF=BE=1,
∴AC=2CF=2,
∴AB=,BC=3,
∴矩形ABCD的面积=AB?BC=3,
故答案为:3.
17.解:∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∵EF⊥FC,
∴∠EFC=∠A=∠D=90°,
∴∠AFE+∠DFC=90°=∠DCF+∠DFC,
∴∠AFE=∠DCF,
在△AFE和△DCF中,
,
∴△AFE≌△DCF(AAS),
∴AE=DF=5cm,
故答案为5.
18.解:∵矩形ABCD中,AB=5,AD=12,∠BAD=∠BCD=90°,
∴BD==13,
∵BP=BA=5,
∴PD=BD﹣BP=8,
∵BA=BP,
∴∠BAP=∠BPA=∠DPQ,
∵AB∥CD,
∴∠BAP=∠DQP,
∴∠DPQ=∠DQP,
∴DQ=DP=8,
∴CQ=DQ﹣CD=DQ﹣AB=8﹣5=3,
∴在Rt△BCQ中,根据勾股定理,得
BQ===3.
故答案为:3.
19.解:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,AC=BF,AO=OC,OD=OB,
∴AO=OC=OD=OB,
∵矩形ABCD被两条对角线分成四个小三角形的周长的和是40厘米,
∴OA+OD+AD+OD+OC+CD+OC+OB+BC+OA+OB+AB=40厘米,
即8OA+2AB+2BC=40厘米,
∵矩形ABCD的周长是22厘米,
∴2AB+2BC=22厘米,
∴8OA=18厘米,
∴OA=2.25厘米,
即AC=BD=2OA=4.5厘米.
故答案为:4.5.
20.解:如图2,设CD与y轴交于点M,作CN⊥y轴于点N,
根据题意可知:∠DOM=30°,OD=3,
∴DM=3?tan30°=,OM=3÷cos30°=2,
∴CM=4﹣,
∵∠NCM=30°,
∴MN=,
则ON=OM+MN=,
∴图2中C点的坐标为(,).
故答案为:(,).
21.解:∵∠BAC=90°,且BA=3,AC=4,
∴BC==5,
∵DM⊥AB,DN⊥AC,
∴∠DMA=∠DNA=∠BAC=90°,
∴四边形DMAN是矩形,
∴MN=AD,
∴当AD⊥BC时,AD的值最小,
此时,△ABC的面积=AB×AC=BC×AD,
∴AD==,
∴MN的最小值为;
故答案为:.
22.解:∵点A(6,0),
∴OA=6,
∵OD=2,
∴AD=OA﹣OD=6﹣2=4,
∵四边形CODE是矩形,
∴DE∥OC,
∴∠AED=∠ABO=30°,
在Rt△AED中,AE=2AD=8,ED===4,
∵OD=2,
∴点E的坐标为(2,4);
∴矩形CODE的面积为4×2=8,
∵将矩形CODE沿x轴向右平移,矩形CODE与△ABO重叠部分的面积为6
∴矩形CODE与△ABO不重叠部分的面积为2,
如图,设ME′=x,则FE′=x,依题意有
x×x÷2=2,
解得x=±2(负值舍去).
故矩形CODE向右平移的距离为2.
故答案为:2.
23.解:如图,
∵四边形ABCD是矩形,
∴CD=AB=6,AD=BC,∠ABC=∠ADC=90°,
∴BC===2,
∴AD=2,
当点E在CD上时,
∵AE2=DE2+AD2=EC2,
∴(6﹣DE)2=DE2+4,
∴DE=;
当点E'在AB上时,
∵CE'2=BE'2+BC2=E'A2,
∴AE'2=(6﹣AE')2+4,
∴AE'=,
∴DE'===,
综上所述:DE=或,
故答案为:或.
24.解:①当DP=AD时,
∵矩形ABCD,
∴DC=AB=3,AD=BC=5,
∵△PAD是等腰三角形,
∴DP=AD=5,
在Rt△PCD中,
PC==4,
∴BP=BC﹣CP=5﹣4=1.
②当AD=AP时,
∴AP=AD=5,
在Rt△ABP中,
由勾股定理得,
BP==4,
③当AP=DP时,
过P作PE⊥AD于点E,
∴AE=AD=2.5,
∵∠B=∠BAE=∠AEP=90°,
∴四边形ABPE是矩形,
∴BP=AE=2.5.
综上所述,BP=1或4或2.5.
25.(1)证明:∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形,
∵∠AOB=∠DAO+∠ADO=2∠OAD,
∴∠DAO=∠ADO,
∴AO=DO,
∴AC=BD,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴AB∥CD,∠BAD=90°,
∴∠ABO=∠CDO,
∵∠AOB:∠ODC=8:5,
∴∠AOB:∠ABO=8:5,
∴∠BAO:∠AOB:∠ABO=5:8:5,
∴∠ABO=50°,
∵∠BAD=90°,
∴∠ADO=90°﹣50°=40°.
26.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵点E,F分别是BC,AD的中点.
∴AF=DF=AD,BE=CE=BC,
∴AF=CE,
∵AF∥EC,
∴四边形AECF是平行四边形;
(2)解:当AB=AC时,四边形AECF是矩形,证明如下:
由(1)得:四边形AECF是平行四边形,
∵AB=AC,
∴△ABC是等腰三角形,
∵点E是BC的中点,
∴AE⊥BC,
∴∠AEC=90°,
∴平行四边形AECF是矩形.
27.证明:(1)连接AC交EF于点O,
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵DE=BF,
∴OE=OF,
∴四边形AFCE是平行四边形;
(2)∵BD⊥AD,AB=5,AD=3,
∴BD===4,
∴BO=DO=2,
∴AO===,
∵四边形AFCE是矩形,
∴AO=CO,EO=FO,AC=EF,
∴AO=EO=,
∴DE=﹣2.
28.解:∵A点坐标为(1,4),B点坐标为(1,1),将线段AB向右平移4个单位得到线段CD,
∴四边形ABCD是矩形,
∴AB=3,BC=4,
由题意可得:,
解得:0≤m≤3,
点P(m,m+1)在直线y=x+1上,当1≤m≤3时,直线y=x+1落在长方形ABCD的内部(包含边界),
所以m的取值范围是1≤m≤3.
29.(1)证明:∵点D、O分别是边BC、AC的中点,
∴OD是△ABC的中位线,BD=CD,
∴OD∥AB,
∴DE∥AB,
∵AE∥BC,
∴四边形ABDE是平行四边形,
∴AE=BD=CD,
∴四边形ADCE是平行四边形,
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴∠ADC=90°,
∴平行四边形ADCE是矩形;
(2)解:长度分别是线段OF长度的4倍的线段为:AB、BC、AC、DE,理由如下:
∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC=BC,
由(1)得:四边形ABDE是平行四边形,四边形ADCE是矩形,
∴BF=EF,OD=OE,AC=DE,
∴OF是△BDE的中位线,
∴BD=2OF,
∵AB=AC=DE=BC=2BD,
∴AB=AC=DE=BC=4OF.
30.解:(1)∵四边形ABCO是矩形,
∴AB∥OC,AB=OC=8,AO=BC=4,BC∥AO,
∴点A(0,4),点B(8,4),点C(8,0);
(2)四边形OPBQ的面积不随t的增大而变化,理由如下:
设运动时间为t秒,则OQ=t,CP=2t,
∴AQ=4﹣t,
∴S△ABQ=×AB×AQ=×8×(4﹣t)=16﹣4t,
S△BCP=×PC×BC=×2t×4=4t,
∴S四边形OPBQ=S矩形ABCO﹣S△ABQ﹣S△BCP=32﹣(16﹣4t)﹣4t=16,
∴四边形OPBQ的面积不随t的增大而变化.
31.证明:(1)∵PQ⊥CP,
∴∠QPC=90°,
∴∠QPA+∠BPC=180°﹣90°=90°,
∵∠QPA=∠PCB,
∴∠BPC+∠PCB=90°,
∴∠B=180°﹣(∠BPC+∠PCB)=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形;
(2)连接CQ,
∵四边形ABCD是矩形,
∴∠D=90°,
∵∠CPQ=90°,
∴在Rt△CDQ和Rt△CPQ中
,
∴Rt△CDQ≌Rt△CPQ(HL),
∴CD=CP.
32.(1)证明:∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∵AB∥CD,
∴∠B+∠C=180°,
又∵∠B=∠C,
∴∠B=∠C=90°,
∴四边形ABCD为矩形;
(2)解:如图2,延长BA,CM交于点E,
∵M为AD的中点,N为AB中点,
∴AN=BN=2,AM=MD,
∴AB=CD=4,
∵AE∥DC,
∴∠E=∠DCM,
在△AEM和△DCM中,
,
∴△AME≌△DCM(AAS),
∴AE=CD=4,
∵∠BNC=2∠DCM=∠E+∠NCE,
∴∠NCE=∠DCM=∠E,
∴CN=EN=AE+AN=4+2=6,
∴BC===4.
33.(1)证明:在矩形ABCD中,∠D=90°,DC∥AB,
∴∠BAN=∠AMD,
∵BN⊥AM,
∴∠BNA=90°,
在△ABN和△MAD中,
,
∴△ABN≌△MAD(AAS);
(2)解:∵△ABN≌△MAD,
∴BN=AD,
∵AD=2,
∴BN=2,
又∵AN=4,
在Rt△ABN中,AB===2,
∴S矩形ABCD=2×2=4,S△ABN=S△MAD=×2×4=4,
∴S四边形BCMN=S矩形ABCD﹣S△ABN﹣S△MAD=4﹣8.
34.(1)证明:∵在矩形ABCD中,O为对角线AC的中点,
∴AD∥BC,AO=CO,
∴∠OAM=∠OCN,∠OMA=∠ONC,
在△AOM和△CON中,
,
∴△AOM≌△CON(AAS),
∴AM=CN,
∵AM∥CN,
∴四边形ANCM为平行四边形;
(2)解:∵在矩形ABCD中,AD=BC,
由(1)知:AM=CN,
∴DM=BN,
∵四边形ANCM为平行四边形,MN⊥AC,
∴平行四边形ANCM为菱形,
∴AM=AN=NC=AD﹣DM,
∴在Rt△ABN中,根据勾股定理,得
AN2=AB2+BN2,
∴(4﹣DM)2=22+DM2,
解得DM=.
35.解:(1)点P从点B出发,以1cm/秒的速度沿BC向点C运动,点P的运动时间为t秒时,BP=tcm,
则PC=(6﹣t)(cm);
∴S△DCP=CP?CD=(6﹣t)×4=(12﹣2t)(cm2),
故答案为(12﹣2t)cm2.
(2)①当BP=CQ,AB=PC时,△ABP≌△PCQ,
∵AB=4cm,
∴PC=4cm,
∴BP=6﹣4=2(cm),
即t=2,
∴CQ=BP=2cm,
∴v×2=2,
解得:v=1;
②当BA=CQ,PB=PC时,△ABP≌△QCP,
∵PB=PC,
∴BP=PC=BC=3,
即t=3,
∴CQ=BA=4cm,
∴v×3=4,
解得:v=.
综上所述:当v=或1时△ABP与△PQC全等.
36.证明:连接BD,CF,
∵四边形ADEC,四边形ABHF是正方形,
∴AB=AF,AD=AC,∠DAC=∠BAF,
∴∠DAB=∠CAF,
在△ADB和△ACF中,
,
∴△ADB≌△ACF(SAS).
∴S△ADB=S△ACF,
由AD∥CE得:S正方形ACED与S△ADB的数量关系满足S正方形ACED=2S△ADB,
同理可得,S矩形AFGP=2S△ACF,
∴S正方形ACED=S矩形AFGP,即b2=S矩形AFGP.
同理,连接AM,CH,通过推理可得,a2=S矩形BHGP.
∴S正方形ACED+S正方形BCNM=S正方形ABHF.
∴a2+b2=c2.
故答案为:△ACF,2S△ADB,S△ACF,S矩形BHGP.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
