1.2矩形的性质与判定 同步培优提升训练 2021—2022学年北师大版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 1.2矩形的性质与判定 同步培优提升训练 2021—2022学年北师大版九年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 329.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 18:35:46 | ||
图片预览


文档简介
2021年北师大版九年级数学上册《1.2矩形的性质与判定》同步培优提升训练(附答案)
1.如图,在矩形ABCD中,AB=12,AD=5,对角线AC的长度为( )
A.12 B.6.5 C.13 D.10
2.矩形和菱形都具有的性质是( )
A.有一组邻边相等 B.对角线互相平分
C.对角线相等 D.对角线互相垂直
3.如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF,AF.若AB=2,AD=3,则∠AEF的大小为( )
A.30° B.45° C.60° D.不能确定
4.如图,在矩形ABCD中,AB=6,AD=5,点P在AD上,点Q在BC上,且AP=CQ,连接CP,QD,则PC+QD的最小值为( )
A.10 B.11 C.12 D.13
5.矩形ABCD的两条对角线的一个夹角为120°,两条对角线的长度之和为24cm,则这个矩形的一条短边的长为( )cm.
A.6 B.12 C.24 D.48
6.如图,点E为矩形ABCD的边BC上的点,DF⊥AE于点F,且DF=AB,下列结论不正确的是( )
A.DE平分∠AEC B.△ADE为等腰三角形
C.AF=AB D.AE=BE+EF
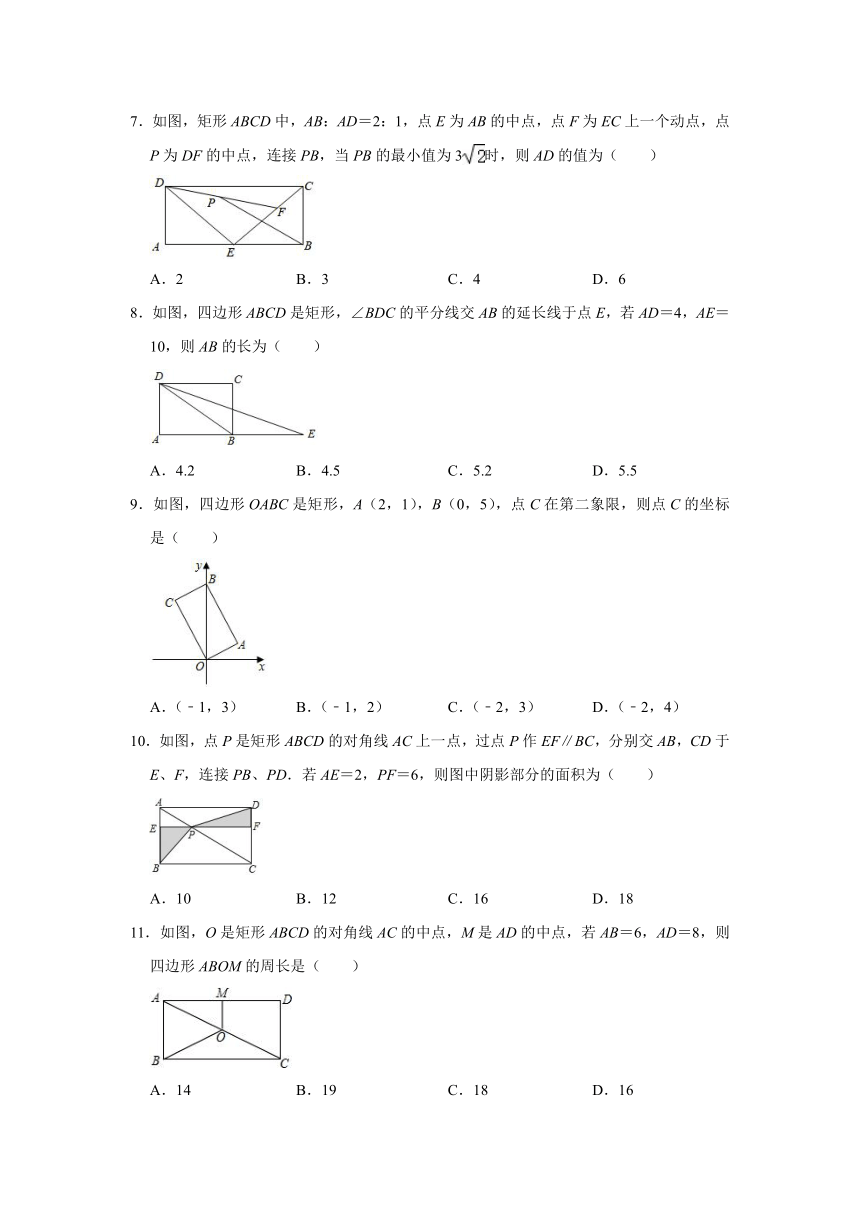
7.如图,矩形ABCD中,AB:AD=2:1,点E为AB的中点,点F为EC上一个动点,点P为DF的中点,连接PB,当PB的最小值为3时,则AD的值为( )
A.2 B.3 C.4 D.6
8.如图,四边形ABCD是矩形,∠BDC的平分线交AB的延长线于点E,若AD=4,AE=10,则AB的长为( )
A.4.2 B.4.5 C.5.2 D.5.5
9.如图,四边形OABC是矩形,A(2,1),B(0,5),点C在第二象限,则点C的坐标是( )
A.(﹣1,3) B.(﹣1,2) C.(﹣2,3) D.(﹣2,4)
10.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB、PD.若AE=2,PF=6,则图中阴影部分的面积为( )
A.10 B.12 C.16 D.18
11.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=6,AD=8,则四边形ABOM的周长是( )
A.14 B.19 C.18 D.16
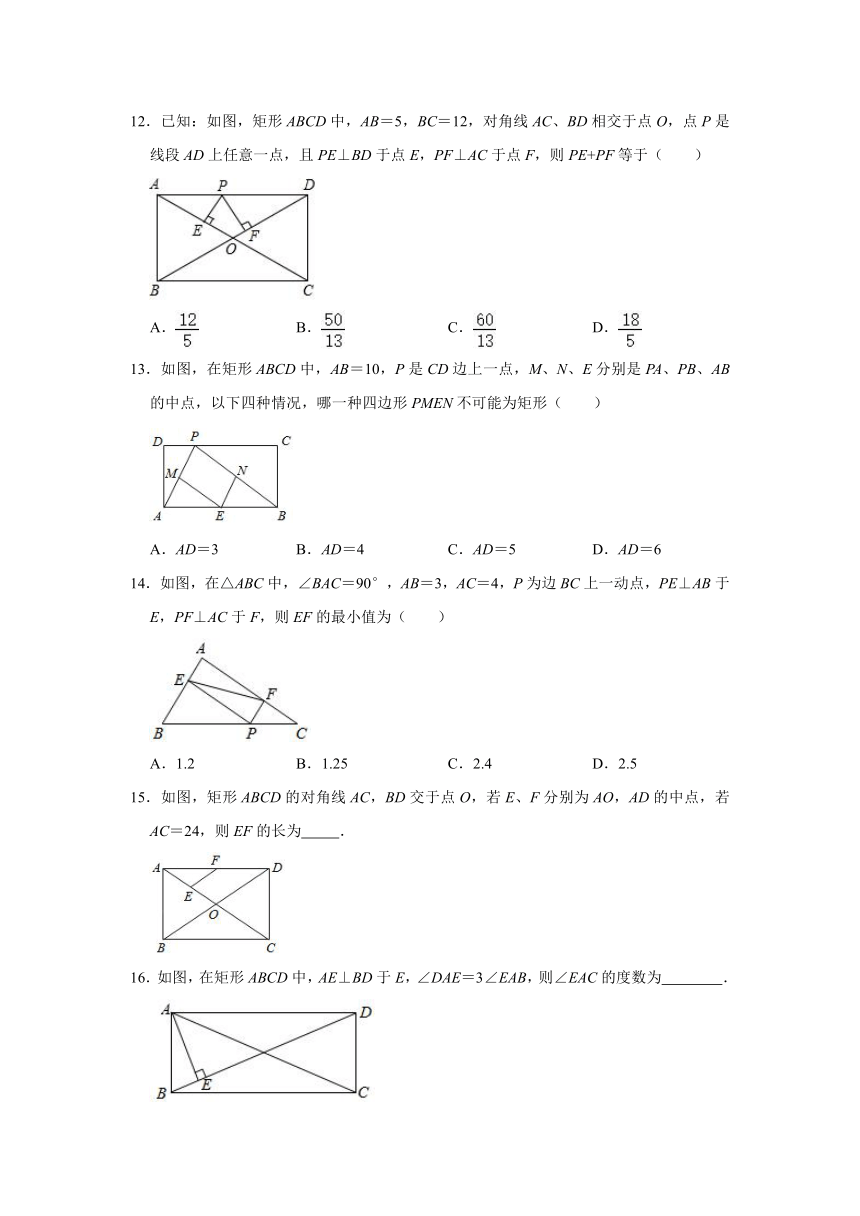
12.已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥BD于点E,PF⊥AC于点F,则PE+PF等于( )
A. B. C. D.
13.如图,在矩形ABCD中,AB=10,P是CD边上一点,M、N、E分别是PA、PB、AB的中点,以下四种情况,哪一种四边形PMEN不可能为矩形( )
A.AD=3 B.AD=4 C.AD=5 D.AD=6
14.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )
A.1.2 B.1.25 C.2.4 D.2.5
15.如图,矩形ABCD的对角线AC,BD交于点O,若E、F分别为AO,AD的中点,若AC=24,则EF的长为 .
16.如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠EAB,则∠EAC的度数为 .
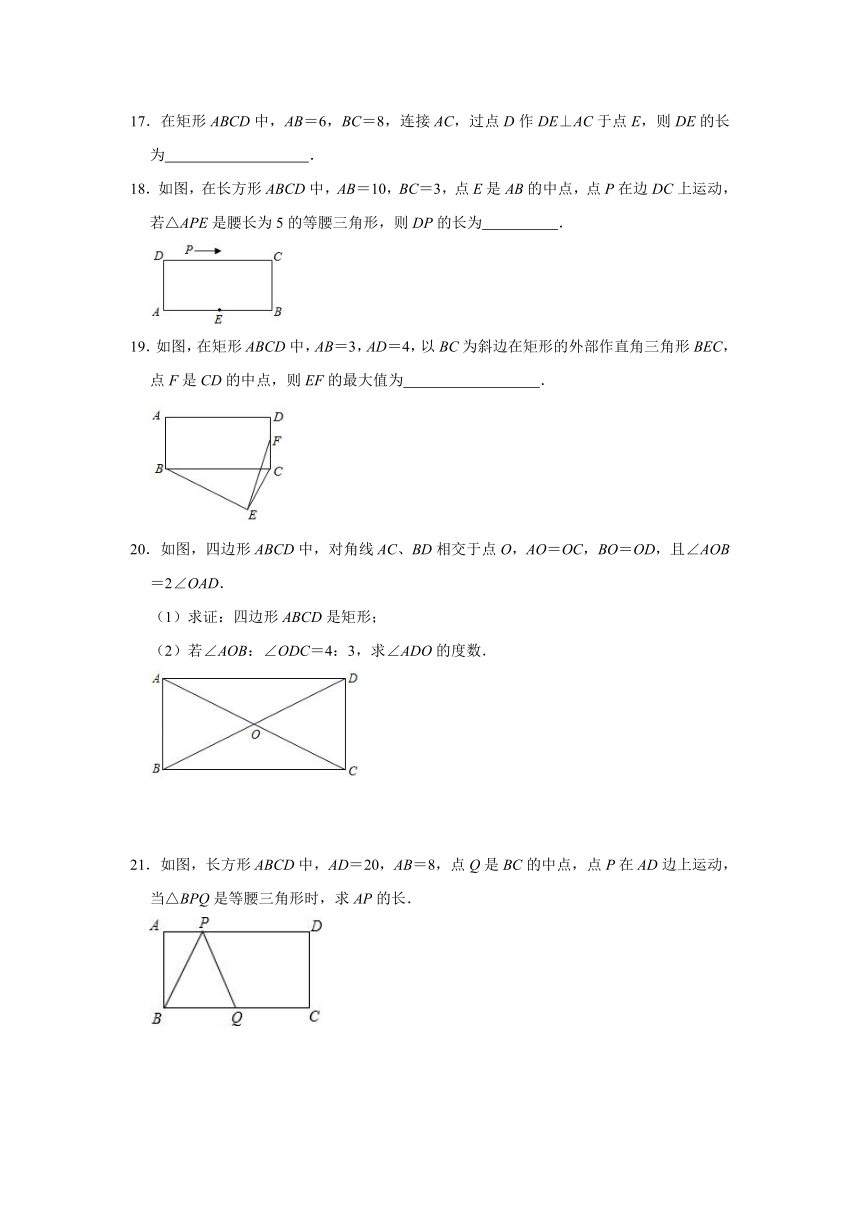
17.在矩形ABCD中,AB=6,BC=8,连接AC,过点D作DE⊥AC于点E,则DE的长为 .
18.如图,在长方形ABCD中,AB=10,BC=3,点E是AB的中点,点P在边DC上运动,若△APE是腰长为5的等腰三角形,则DP的长为 .
19.如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为 .
20.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB:∠ODC=4:3,求∠ADO的度数.
21.如图,长方形ABCD中,AD=20,AB=8,点Q是BC的中点,点P在AD边上运动,当△BPQ是等腰三角形时,求AP的长.
22.如图,点E在矩形ABCD的边BC上,延长EB到点F,使BF=CE,连接AF.求证:AD=EF.
23.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE∥AC交BA的延长线于点E.
(1)求证:DB=DE;
(2)若∠AOB=60°,BD=4,求四边形BCDE的面积.
24.如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
(3)经过多长时间,当PQ不平行于CD时,有PQ=CD.
参考答案
1.解:∵四边形ABCD是矩形,
∴∠ADC=90°,CD=AB=12,
∵AD=5,
∴在Rt△ADC中,
AC====13,
故选:C.
2.解:矩形的性质是:①矩形的四个角度数直角,②矩形的对边相等且互相平行,③矩形对角线相等且互相平分;
菱形的性质是:①菱形的四条边都相等,菱形的对边互相平行;②菱形的对角相等,③菱形的对角线互相平分且垂直,并且每条对角线平分一组对角,
所以矩形和菱形都具有的性质是对角线互相平分,
故选:B.
3.解:∵四边形ABCD是矩形,AD=3,AB=2,
∴∠B=∠C=90°,CD=AB=2,BC=AD=3,
∵点E是CD的中点,FC=2BF,
∴CE=DE=1,BF=1,CF=2,
∴AB=CF=2,CE=BF=1,
在△ABF和△FCE中,
,
∴△ABF≌△FCE(SAS),
∴AF=EF,∠BAF=∠CFE,
∵∠B=90°,
∴∠BAF+∠AFB=90°,
∴∠CFE+∠AFB=90°,
∴∠AFE=180°﹣(∠CFE+∠AFB)=180°﹣9°=90°,
∴△AFE是等腰直角三角形,
∴∠AEF=45°,
故选:B.
4.解:如图,连接BP,
在矩形ABCD中,AD∥BC,AD=BC,
∵AP=CQ,
∴AD﹣AP=BC﹣CQ,
∴DP=QB,DP∥BQ,
∴四边形DPBQ是平行四边形,
∴PB∥DQ,PB=DQ,
则PC+QD=PC+PB,则PC+QD的最小值转化为PC+PB的最小值,
在BA的延长线上截取AE=AB=6,连接PE,
∵PA⊥BE,
∴PA是BE的垂直平分线,
∴PB=PE,
∴PC+PB=PC+PE,
连接CE,则PC+QD=PC+PB=PC+PE≥CE,
∵BE=2AB=12,BC=AD=5,
∴CE==13.
∴PC+PB的最小值为13.
故选:D.
5.解:如图所示,
∵四边形ABCD是矩形,两条对角线的长度之和为24cm,
∴AC=BD=12cm,OA=OB=AC=6cm,
由题意可知,∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=6cm.
故选:A.
6.解:∵四边形ABCD是矩形,
∴∠C=∠ABE=90°,AD∥BC,AB=CD,
∵DF=AB,
∴DF=CD,
∵DF⊥AE,
∴∠DFA=∠DFE=90°,
在Rt△DEF和Rt△DEC中,,
∴Rt△DEF≌Rt△DEC(HL),
∴∠FED=∠CED,
∴DE平分∠AEC;
故A正确;
∵AD∥BC,
∴∠AEB=∠DAF,
在△ABE和△AFD中,
,
∴△ABE≌△DFA(AAS),
∴AE=AD,
∴△ADE为等腰三角形;
故B正确;
∵△ABE≌△DFA,
∴不存在AF=AB,
故C错误;
∵△ABE≌△DFA,
∴BE=FA,
∴AE=AF+EF=BE+EF.
故D正确.
故选:C.
7.解:如图,
当点F与点C重合时,点P在P1处,CP1=DP1,
当点F与点E重合时,点P在P2处,EP2=DP2,
∴P1P2∥CE且P1P2=CE..
且当点F在EC上除点C、E的位置处时,有DP=FP.
由中位线定理可知:P1P∥CE且P1P=CF,
∴点P的运动轨迹是线段P1P2,
.∴当BP⊥P1P2时,PB取得最小值.
∵矩形ABCD中,AB:AD=2:1,设AB=2t,则AD=t,
∵E为AB的中点,
∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=t,
∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°.
∴∠DP2P1=90°.
∴∠DP1P2=45°.
∴∠P2P1B=90°,即BP1⊥P1P2,
∴BP的最小值为BP1的长.
在等腰直角△BCP1中,CP1=BC=t,
∴BP1=t=3,
∴t=3.
故选:B.
8.解:如图,∵四边形ABCD是矩形,
∴CD∥AB,
∴∠1=∠E.
又∵∠BDC的平分线交AB的延长线于点E,
∴∠1=∠2,
∴∠2=∠E.
∴BE=BD.
∵AE=10,
∴BD=BE=10﹣AB.
在直角△ABD中,AD=4,BD=10﹣AB,则由勾股定理知:AB==.
∴AB=4.2.
故选:A.
9.解:过C作CE⊥y轴于E,过A作AF⊥y轴于F,
∴∠CEO=∠AFB=90°,
∵四边形ABCO是矩形,
∴AB=OC,AB∥OC,
∴∠ABF=∠COE,
∴△OCE≌△ABF(AAS),
同理△BCE≌△OAF,
∴CE=AF,OE=BF,BE=OF,
∵A(2,1),B(0,5),
∴AF=CE=2,BE=OF=1,OB=5,
∴OE=4,
∴点C的坐标是(﹣2,4);
故选:D.
10.解:作PM⊥AD于M,交BC于N.
则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,
∴S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,
∵MP=AE=2
∴S△DFP=S△PBE=×2×6=6,
∴S阴=6+6=12,
故选:B.
11.解:∵四边形ABCD是矩形,
∴AD=BC=8,AB=CD=6,∠ABC=90°,
∴AC==10,
∵AO=OC,
∴BO=AC=5,
∵AO=OC,AM=MD=4,
∴OM=CD=3,
∴四边形ABOM的周长为AB+OB+OM+AM=6+5+3+4=18.
故选:C.
12.解:连接PO,
∵矩形ABCD的两边AB=5,BC=12,
∴S矩形ABCD=AB?BC=60,OA=OC,OB=OD,AC=BD,AC===13,
∴S△AOD=S矩形ABCD=15,OA=OD=AC=,
∴S△AOD=S△AOP+S△DOP=OA?PE+OD?PF=OA(PE+PF)=××(PE+PF)=15,
∴PE+PF=,
故选:C.
13.解:∵四边形ABCD是矩形,
∴AD=BC,AB=CD=10,∠C=∠D=90°,
∵M、N、E分别是PA、PB、AB的中点,
∴ME、NE是△ABP的中位线,
∴ME∥BP,NE∥AP,
∴四边形PMEN是平行四边形,
当∠APB=90°时,四边形PMEN是矩形,
设DP=x,CP=10﹣x,
由勾股定理得:AP2=AD2+x2,BP2=BC2+(10﹣x)2,AP2+BP2=AB2,
∴AD2+x2+AD2+(10﹣x)2=102,
AD2+x2﹣10x=0,
①当AD=3时,x2﹣10x+9=0,
x=1或x=9,符合题意;
②当AD=4时,x2﹣10x+16=0,
x=2或x=8,符合题意;
③当AD=5时,x2﹣10x+25=0,
x=5,符合题意;
④当AD=6时,x2﹣10x+36=0,无解;
故选:D.
14.解:连接AP,如图:
∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=90°,
∵∠BAC=90°,
∴四边形AFPE是矩形,
∴EF=AP,
要使EF最小,只要AP最小即可,
当AP⊥BC时,AP最短,
∵∠BAC=90°,AB=3,AC=4,
∴BC===5,
∵△ABC的面积=×4×3=×5×AP,
∴AP=2.4,
即EF=2.4,
故选:C.
15.解:∵四边形ABCD是矩形,
∴AC=BD=24,OA=OB=OD=OB=12,
∵E、F分别为AO,AD的中点,
∴EF=OD=6,
故答案为:6.
16.解:∵四边形ABCD是矩形,AC、BD是矩形的对角线且相交于O,
∴OA=OB,
∴∠BAC=∠ABD,
∵∠DAE=3∠BAE,∠DAE+∠BAE=90°,
∴∠BAE=22.5°,∠DAE=67.5°.
∵在矩形ABCD,∠DAE+∠ADB=90°,∠ADB+∠ABD=90°,
∴∠ABD=∠DAE=67.5°,即∠BAC=∠ABD=67.5°,
∴∠EAC=∠BAC﹣∠BAE=67.5°﹣22.5°=45°,
故答案为:45°.
17.解:如图,
∵四边形ABCD是矩形,
∴AB=CD=6,BC=AD=8,∠ADC=90°,
∴AC===10,
∵S△ADC=×AD×CD=×AC×DE,
∴DE==,
故答案为:.
18.解:∵AB=10,E为AB的中点,
∴AE=BE=5,
∵四边形ABCD是矩形,BC=3,
∴AD=BC=3,∠D=90°,
有三种情况:①AP=PE=5,作AE的垂直平分线MN,MN交AB于N,
此时P在AE的垂直平分线MN上,
即AN=NE=2.5,则DP=AN=2.5,
∵AD2+DP2=32+2.52≠52,
即此时不存在;
②当AP=AE=5时,由勾股定理得:DP===4;
③当PE=AE=5时,有P和P′两种情况,过P作PN⊥AB于N,
由勾股定理得:NE===4,
即DP=5﹣4=1;DP′=5+4=9,
所以DP的长是4或1或9,
故答案为:4或1或9.
19.解:如图,取BC中点O,连接OE,OF,
∵四边形ABCD是矩形,
∴AB=CD=3,AD=BC=4,∠DCB=90°,
∵点F是CD中点,点O是BC的中点,
∴CF=,CO=2,
∴OF==,
∵点O是Rt△BCE的斜边BC的中点,
∴OE=OC=2,
∵根据三角形三边关系可得:OE+OF≥EF,
∴当点O,点E,点F共线时,EF最大值为OE+OF=2+=.
故答案为:.
20.(1)证明:∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形,
∵∠AOB=∠DAO+∠ADO=2∠OAD,
∴∠DAO=∠ADO,
∴AO=DO,
∴AC=BD,
∴四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠ABO=∠CDO,
∵∠AOB:∠ODC=4:3,
∴∠AOB:∠ABO=4:3,
∴∠BAO:∠AOB:∠ABO=3:4:3,
∴∠ABO=54°,
∵∠BAD=90°,
∴∠ADO=90°﹣54°=36°.
21.解:∵四边形ABCD为矩形,AD=20,
∴BQ=10,
①当BP=PQ时,过P作PM⊥BQ,交BQ于点M,如图1所示:
则BM=MQ=5,且四边形ABMP为矩形,
∴AP=BM=5,
②当BQ=BP时,则BP=10,在Rt△ABP中,AB=8,由勾股定理可求得AP=6,
③当PQ=BQ时,以点Q为圆心,BQ为半径作圆,于AD交于R、S两点,如图2所示:
过Q作QN⊥RS,交RS于点N,则可知RN=SN,
在Rt△RNQ中,可求得RN=SN=6,
则AR=4,AS=16,
即R、S为满足条件的P点的位置,
∴AP=4或16,
综上可知AP为4或5或6或16,
故答案为:4或5或6或16.
22.证明:∵四边形ABCD是矩形,
∴AD=BC,
∵EF=BF+BE,
∵BC=CE+BE,BF=CE,
∴EF=BC,
∴AD=EF.
23.证明:(1)∵四边形ABCD是矩形,
∴AB=CD,AC=BD,AB∥CD,
又∵DE∥AC,
∴四边形ACDE是平行四边形,
∴DE=AC,CD=AE,
∴DE=BD;
(2)∵四边形ABCD是矩形,
∴AC=BD=4,AO=CO,BO=DO,
∴AO=BO=2,
又∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO=2=CD=AE,
∴AD===2,
∴四边形BCDE的面积=×2×2+2×2=6.
24.解:(1)设经过x(s),四边形PQCD为平行四边形
即PD=CQ
所以24﹣x=3x,
解得:x=6.
(2)设经过y(s),四边形PQBA为矩形,
即AP=BQ,
所以y=26﹣3y,
解得:y=.
(3)设经过t(s),四边形PQCD是等腰梯形.
过Q点作QE⊥AD,过D点作DF⊥BC,
∴∠QEP=∠DFC=90°
∵四边形PQCD是等腰梯形,
∴PQ=DC.
又∵AD∥BC,∠B=90°,
∴AB=QE=DF.
在Rt△EQP和Rt△FDC中,
,
∴Rt△EQP≌Rt△FDC(HL).
∴FC=EP=BC﹣AD=26﹣24=2.
又∵AE=BQ=26﹣3t,
∴EP=AP﹣AE=t﹣(26﹣3t)=2.
得:t=7.
∴经过7s,PQ=CD.
1.如图,在矩形ABCD中,AB=12,AD=5,对角线AC的长度为( )
A.12 B.6.5 C.13 D.10
2.矩形和菱形都具有的性质是( )
A.有一组邻边相等 B.对角线互相平分
C.对角线相等 D.对角线互相垂直
3.如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF,AF.若AB=2,AD=3,则∠AEF的大小为( )
A.30° B.45° C.60° D.不能确定
4.如图,在矩形ABCD中,AB=6,AD=5,点P在AD上,点Q在BC上,且AP=CQ,连接CP,QD,则PC+QD的最小值为( )
A.10 B.11 C.12 D.13
5.矩形ABCD的两条对角线的一个夹角为120°,两条对角线的长度之和为24cm,则这个矩形的一条短边的长为( )cm.
A.6 B.12 C.24 D.48
6.如图,点E为矩形ABCD的边BC上的点,DF⊥AE于点F,且DF=AB,下列结论不正确的是( )
A.DE平分∠AEC B.△ADE为等腰三角形
C.AF=AB D.AE=BE+EF
7.如图,矩形ABCD中,AB:AD=2:1,点E为AB的中点,点F为EC上一个动点,点P为DF的中点,连接PB,当PB的最小值为3时,则AD的值为( )
A.2 B.3 C.4 D.6
8.如图,四边形ABCD是矩形,∠BDC的平分线交AB的延长线于点E,若AD=4,AE=10,则AB的长为( )
A.4.2 B.4.5 C.5.2 D.5.5
9.如图,四边形OABC是矩形,A(2,1),B(0,5),点C在第二象限,则点C的坐标是( )
A.(﹣1,3) B.(﹣1,2) C.(﹣2,3) D.(﹣2,4)
10.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB、PD.若AE=2,PF=6,则图中阴影部分的面积为( )
A.10 B.12 C.16 D.18
11.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=6,AD=8,则四边形ABOM的周长是( )
A.14 B.19 C.18 D.16
12.已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥BD于点E,PF⊥AC于点F,则PE+PF等于( )
A. B. C. D.
13.如图,在矩形ABCD中,AB=10,P是CD边上一点,M、N、E分别是PA、PB、AB的中点,以下四种情况,哪一种四边形PMEN不可能为矩形( )
A.AD=3 B.AD=4 C.AD=5 D.AD=6
14.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )
A.1.2 B.1.25 C.2.4 D.2.5
15.如图,矩形ABCD的对角线AC,BD交于点O,若E、F分别为AO,AD的中点,若AC=24,则EF的长为 .
16.如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠EAB,则∠EAC的度数为 .
17.在矩形ABCD中,AB=6,BC=8,连接AC,过点D作DE⊥AC于点E,则DE的长为 .
18.如图,在长方形ABCD中,AB=10,BC=3,点E是AB的中点,点P在边DC上运动,若△APE是腰长为5的等腰三角形,则DP的长为 .
19.如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为 .
20.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB:∠ODC=4:3,求∠ADO的度数.
21.如图,长方形ABCD中,AD=20,AB=8,点Q是BC的中点,点P在AD边上运动,当△BPQ是等腰三角形时,求AP的长.
22.如图,点E在矩形ABCD的边BC上,延长EB到点F,使BF=CE,连接AF.求证:AD=EF.
23.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE∥AC交BA的延长线于点E.
(1)求证:DB=DE;
(2)若∠AOB=60°,BD=4,求四边形BCDE的面积.
24.如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
(3)经过多长时间,当PQ不平行于CD时,有PQ=CD.
参考答案
1.解:∵四边形ABCD是矩形,
∴∠ADC=90°,CD=AB=12,
∵AD=5,
∴在Rt△ADC中,
AC====13,
故选:C.
2.解:矩形的性质是:①矩形的四个角度数直角,②矩形的对边相等且互相平行,③矩形对角线相等且互相平分;
菱形的性质是:①菱形的四条边都相等,菱形的对边互相平行;②菱形的对角相等,③菱形的对角线互相平分且垂直,并且每条对角线平分一组对角,
所以矩形和菱形都具有的性质是对角线互相平分,
故选:B.
3.解:∵四边形ABCD是矩形,AD=3,AB=2,
∴∠B=∠C=90°,CD=AB=2,BC=AD=3,
∵点E是CD的中点,FC=2BF,
∴CE=DE=1,BF=1,CF=2,
∴AB=CF=2,CE=BF=1,
在△ABF和△FCE中,
,
∴△ABF≌△FCE(SAS),
∴AF=EF,∠BAF=∠CFE,
∵∠B=90°,
∴∠BAF+∠AFB=90°,
∴∠CFE+∠AFB=90°,
∴∠AFE=180°﹣(∠CFE+∠AFB)=180°﹣9°=90°,
∴△AFE是等腰直角三角形,
∴∠AEF=45°,
故选:B.
4.解:如图,连接BP,
在矩形ABCD中,AD∥BC,AD=BC,
∵AP=CQ,
∴AD﹣AP=BC﹣CQ,
∴DP=QB,DP∥BQ,
∴四边形DPBQ是平行四边形,
∴PB∥DQ,PB=DQ,
则PC+QD=PC+PB,则PC+QD的最小值转化为PC+PB的最小值,
在BA的延长线上截取AE=AB=6,连接PE,
∵PA⊥BE,
∴PA是BE的垂直平分线,
∴PB=PE,
∴PC+PB=PC+PE,
连接CE,则PC+QD=PC+PB=PC+PE≥CE,
∵BE=2AB=12,BC=AD=5,
∴CE==13.
∴PC+PB的最小值为13.
故选:D.
5.解:如图所示,
∵四边形ABCD是矩形,两条对角线的长度之和为24cm,
∴AC=BD=12cm,OA=OB=AC=6cm,
由题意可知,∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=6cm.
故选:A.
6.解:∵四边形ABCD是矩形,
∴∠C=∠ABE=90°,AD∥BC,AB=CD,
∵DF=AB,
∴DF=CD,
∵DF⊥AE,
∴∠DFA=∠DFE=90°,
在Rt△DEF和Rt△DEC中,,
∴Rt△DEF≌Rt△DEC(HL),
∴∠FED=∠CED,
∴DE平分∠AEC;
故A正确;
∵AD∥BC,
∴∠AEB=∠DAF,
在△ABE和△AFD中,
,
∴△ABE≌△DFA(AAS),
∴AE=AD,
∴△ADE为等腰三角形;
故B正确;
∵△ABE≌△DFA,
∴不存在AF=AB,
故C错误;
∵△ABE≌△DFA,
∴BE=FA,
∴AE=AF+EF=BE+EF.
故D正确.
故选:C.
7.解:如图,
当点F与点C重合时,点P在P1处,CP1=DP1,
当点F与点E重合时,点P在P2处,EP2=DP2,
∴P1P2∥CE且P1P2=CE..
且当点F在EC上除点C、E的位置处时,有DP=FP.
由中位线定理可知:P1P∥CE且P1P=CF,
∴点P的运动轨迹是线段P1P2,
.∴当BP⊥P1P2时,PB取得最小值.
∵矩形ABCD中,AB:AD=2:1,设AB=2t,则AD=t,
∵E为AB的中点,
∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=t,
∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°.
∴∠DP2P1=90°.
∴∠DP1P2=45°.
∴∠P2P1B=90°,即BP1⊥P1P2,
∴BP的最小值为BP1的长.
在等腰直角△BCP1中,CP1=BC=t,
∴BP1=t=3,
∴t=3.
故选:B.
8.解:如图,∵四边形ABCD是矩形,
∴CD∥AB,
∴∠1=∠E.
又∵∠BDC的平分线交AB的延长线于点E,
∴∠1=∠2,
∴∠2=∠E.
∴BE=BD.
∵AE=10,
∴BD=BE=10﹣AB.
在直角△ABD中,AD=4,BD=10﹣AB,则由勾股定理知:AB==.
∴AB=4.2.
故选:A.
9.解:过C作CE⊥y轴于E,过A作AF⊥y轴于F,
∴∠CEO=∠AFB=90°,
∵四边形ABCO是矩形,
∴AB=OC,AB∥OC,
∴∠ABF=∠COE,
∴△OCE≌△ABF(AAS),
同理△BCE≌△OAF,
∴CE=AF,OE=BF,BE=OF,
∵A(2,1),B(0,5),
∴AF=CE=2,BE=OF=1,OB=5,
∴OE=4,
∴点C的坐标是(﹣2,4);
故选:D.
10.解:作PM⊥AD于M,交BC于N.
则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,
∴S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,
∵MP=AE=2
∴S△DFP=S△PBE=×2×6=6,
∴S阴=6+6=12,
故选:B.
11.解:∵四边形ABCD是矩形,
∴AD=BC=8,AB=CD=6,∠ABC=90°,
∴AC==10,
∵AO=OC,
∴BO=AC=5,
∵AO=OC,AM=MD=4,
∴OM=CD=3,
∴四边形ABOM的周长为AB+OB+OM+AM=6+5+3+4=18.
故选:C.
12.解:连接PO,
∵矩形ABCD的两边AB=5,BC=12,
∴S矩形ABCD=AB?BC=60,OA=OC,OB=OD,AC=BD,AC===13,
∴S△AOD=S矩形ABCD=15,OA=OD=AC=,
∴S△AOD=S△AOP+S△DOP=OA?PE+OD?PF=OA(PE+PF)=××(PE+PF)=15,
∴PE+PF=,
故选:C.
13.解:∵四边形ABCD是矩形,
∴AD=BC,AB=CD=10,∠C=∠D=90°,
∵M、N、E分别是PA、PB、AB的中点,
∴ME、NE是△ABP的中位线,
∴ME∥BP,NE∥AP,
∴四边形PMEN是平行四边形,
当∠APB=90°时,四边形PMEN是矩形,
设DP=x,CP=10﹣x,
由勾股定理得:AP2=AD2+x2,BP2=BC2+(10﹣x)2,AP2+BP2=AB2,
∴AD2+x2+AD2+(10﹣x)2=102,
AD2+x2﹣10x=0,
①当AD=3时,x2﹣10x+9=0,
x=1或x=9,符合题意;
②当AD=4时,x2﹣10x+16=0,
x=2或x=8,符合题意;
③当AD=5时,x2﹣10x+25=0,
x=5,符合题意;
④当AD=6时,x2﹣10x+36=0,无解;
故选:D.
14.解:连接AP,如图:
∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=90°,
∵∠BAC=90°,
∴四边形AFPE是矩形,
∴EF=AP,
要使EF最小,只要AP最小即可,
当AP⊥BC时,AP最短,
∵∠BAC=90°,AB=3,AC=4,
∴BC===5,
∵△ABC的面积=×4×3=×5×AP,
∴AP=2.4,
即EF=2.4,
故选:C.
15.解:∵四边形ABCD是矩形,
∴AC=BD=24,OA=OB=OD=OB=12,
∵E、F分别为AO,AD的中点,
∴EF=OD=6,
故答案为:6.
16.解:∵四边形ABCD是矩形,AC、BD是矩形的对角线且相交于O,
∴OA=OB,
∴∠BAC=∠ABD,
∵∠DAE=3∠BAE,∠DAE+∠BAE=90°,
∴∠BAE=22.5°,∠DAE=67.5°.
∵在矩形ABCD,∠DAE+∠ADB=90°,∠ADB+∠ABD=90°,
∴∠ABD=∠DAE=67.5°,即∠BAC=∠ABD=67.5°,
∴∠EAC=∠BAC﹣∠BAE=67.5°﹣22.5°=45°,
故答案为:45°.
17.解:如图,
∵四边形ABCD是矩形,
∴AB=CD=6,BC=AD=8,∠ADC=90°,
∴AC===10,
∵S△ADC=×AD×CD=×AC×DE,
∴DE==,
故答案为:.
18.解:∵AB=10,E为AB的中点,
∴AE=BE=5,
∵四边形ABCD是矩形,BC=3,
∴AD=BC=3,∠D=90°,
有三种情况:①AP=PE=5,作AE的垂直平分线MN,MN交AB于N,
此时P在AE的垂直平分线MN上,
即AN=NE=2.5,则DP=AN=2.5,
∵AD2+DP2=32+2.52≠52,
即此时不存在;
②当AP=AE=5时,由勾股定理得:DP===4;
③当PE=AE=5时,有P和P′两种情况,过P作PN⊥AB于N,
由勾股定理得:NE===4,
即DP=5﹣4=1;DP′=5+4=9,
所以DP的长是4或1或9,
故答案为:4或1或9.
19.解:如图,取BC中点O,连接OE,OF,
∵四边形ABCD是矩形,
∴AB=CD=3,AD=BC=4,∠DCB=90°,
∵点F是CD中点,点O是BC的中点,
∴CF=,CO=2,
∴OF==,
∵点O是Rt△BCE的斜边BC的中点,
∴OE=OC=2,
∵根据三角形三边关系可得:OE+OF≥EF,
∴当点O,点E,点F共线时,EF最大值为OE+OF=2+=.
故答案为:.
20.(1)证明:∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形,
∵∠AOB=∠DAO+∠ADO=2∠OAD,
∴∠DAO=∠ADO,
∴AO=DO,
∴AC=BD,
∴四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠ABO=∠CDO,
∵∠AOB:∠ODC=4:3,
∴∠AOB:∠ABO=4:3,
∴∠BAO:∠AOB:∠ABO=3:4:3,
∴∠ABO=54°,
∵∠BAD=90°,
∴∠ADO=90°﹣54°=36°.
21.解:∵四边形ABCD为矩形,AD=20,
∴BQ=10,
①当BP=PQ时,过P作PM⊥BQ,交BQ于点M,如图1所示:
则BM=MQ=5,且四边形ABMP为矩形,
∴AP=BM=5,
②当BQ=BP时,则BP=10,在Rt△ABP中,AB=8,由勾股定理可求得AP=6,
③当PQ=BQ时,以点Q为圆心,BQ为半径作圆,于AD交于R、S两点,如图2所示:
过Q作QN⊥RS,交RS于点N,则可知RN=SN,
在Rt△RNQ中,可求得RN=SN=6,
则AR=4,AS=16,
即R、S为满足条件的P点的位置,
∴AP=4或16,
综上可知AP为4或5或6或16,
故答案为:4或5或6或16.
22.证明:∵四边形ABCD是矩形,
∴AD=BC,
∵EF=BF+BE,
∵BC=CE+BE,BF=CE,
∴EF=BC,
∴AD=EF.
23.证明:(1)∵四边形ABCD是矩形,
∴AB=CD,AC=BD,AB∥CD,
又∵DE∥AC,
∴四边形ACDE是平行四边形,
∴DE=AC,CD=AE,
∴DE=BD;
(2)∵四边形ABCD是矩形,
∴AC=BD=4,AO=CO,BO=DO,
∴AO=BO=2,
又∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO=2=CD=AE,
∴AD===2,
∴四边形BCDE的面积=×2×2+2×2=6.
24.解:(1)设经过x(s),四边形PQCD为平行四边形
即PD=CQ
所以24﹣x=3x,
解得:x=6.
(2)设经过y(s),四边形PQBA为矩形,
即AP=BQ,
所以y=26﹣3y,
解得:y=.
(3)设经过t(s),四边形PQCD是等腰梯形.
过Q点作QE⊥AD,过D点作DF⊥BC,
∴∠QEP=∠DFC=90°
∵四边形PQCD是等腰梯形,
∴PQ=DC.
又∵AD∥BC,∠B=90°,
∴AB=QE=DF.
在Rt△EQP和Rt△FDC中,
,
∴Rt△EQP≌Rt△FDC(HL).
∴FC=EP=BC﹣AD=26﹣24=2.
又∵AE=BQ=26﹣3t,
∴EP=AP﹣AE=t﹣(26﹣3t)=2.
得:t=7.
∴经过7s,PQ=CD.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
