2021--2022学年北师大版数学九年级上册1.1《菱形的性质与判定》课时练习(Word版 含答案)
文档属性
| 名称 | 2021--2022学年北师大版数学九年级上册1.1《菱形的性质与判定》课时练习(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 129.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 19:49:09 | ||
图片预览

文档简介
北师大版数学九年级上册1.1
《菱形的性质与判定》课时练习
一、选择题
1.下列命题中错误的是( )
A.平行四边形的对角线互相平分
B.菱形的对角线互相垂直
C.同旁内角互补
D.矩形的对角线相等
2.平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-3,0),B(0,2),C(3,0),D(0,-2),则四边形ABCD是( )
A.矩形 B.菱形 C.正方形 D.梯形
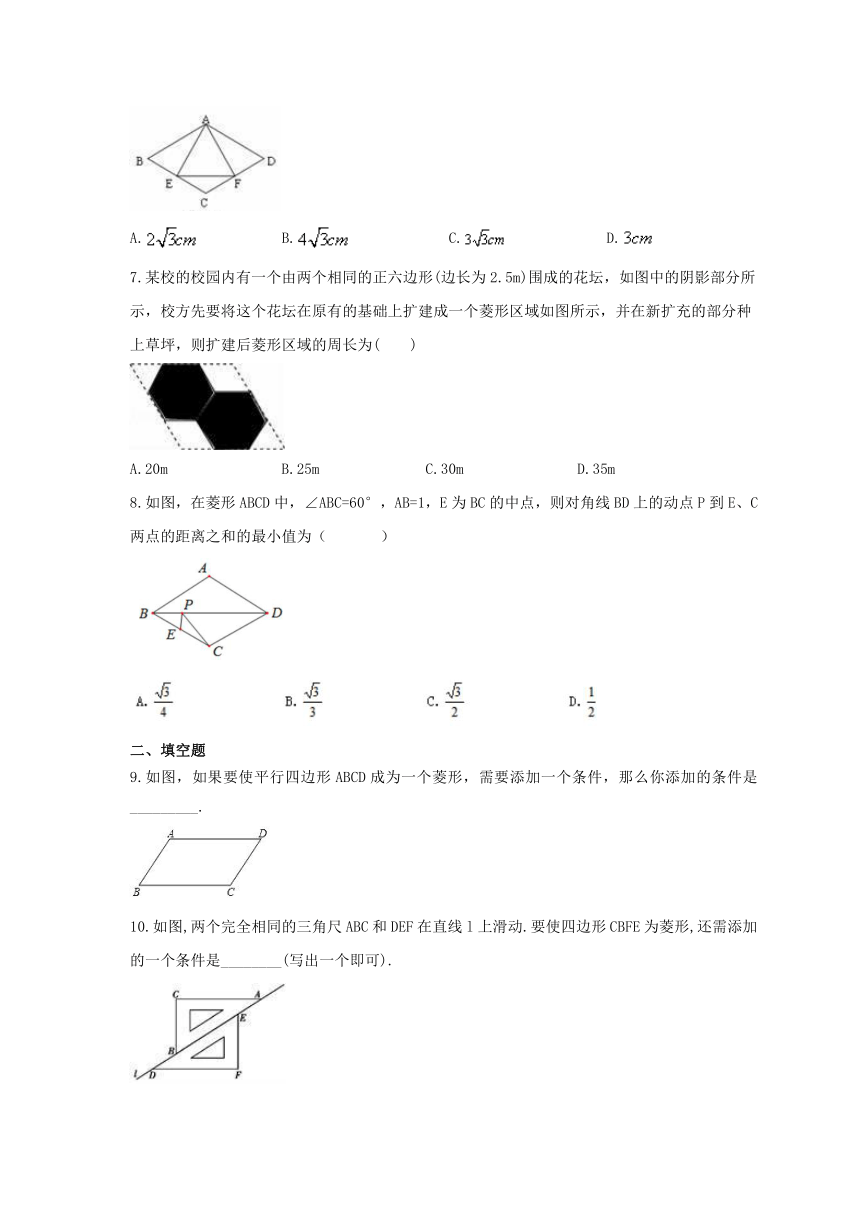
3.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( )
A.28°???????? B.52°???????? C.62°???????? D.72°
4.菱形的两条对角线长分别是6和8,则此菱形的边长是( )
A.10 B.8 C.6 D.5
5.如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,
且∠CDF=24°,则∠DAB等于( )
??
A.100°???? ?? B.104°?? ??C.105°? ?? ??? ??D.110°
6.如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连结AE、EF、AF,则△AEF的周长为(???? )
A.? ? ? B.???? ??C.?? ? D.
7.某校的校园内有一个由两个相同的正六边形(边长为2.5m)围成的花坛,如图中的阴影部分所示,校方先要将这个花坛在原有的基础上扩建成一个菱形区域如图所示,并在新扩充的部分种上草坪,则扩建后菱形区域的周长为( )
A.20m? B.25m? C.30m? D.35m
8.如图,在菱形ABCD中,∠ABC=60°,AB=1,E为BC的中点,则对角线BD上的动点P到E、C两点的距离之和的最小值为( )
二、填空题
9.如图,如果要使平行四边形ABCD成为一个菱形,需要添加一个条件,那么你添加的条件是_________.
10.如图,两个完全相同的三角尺ABC和DEF在直线l上滑动.要使四边形CBFE为菱形,还需添加的一个条件是________(写出一个即可).
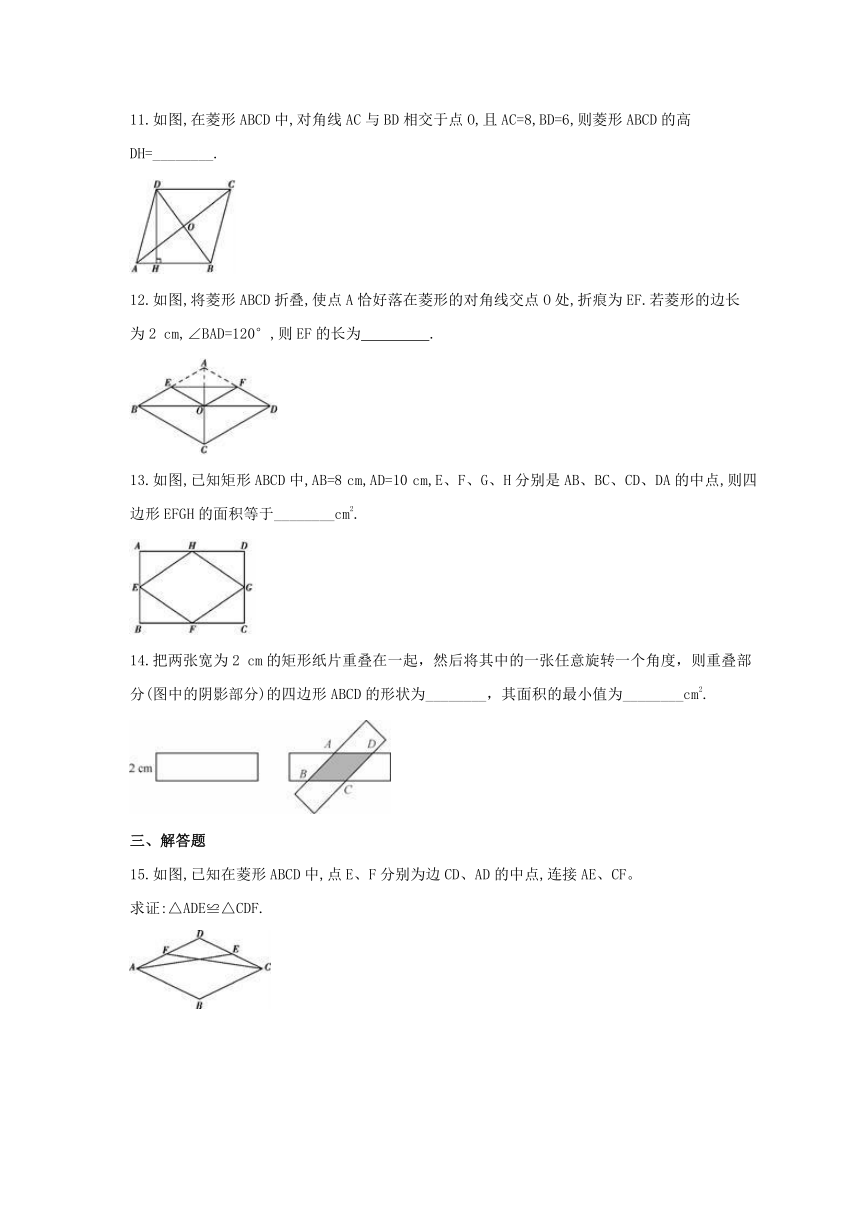
11.如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH=________.
12.如图,将菱形ABCD折叠,使点A恰好落在菱形的对角线交点O处,折痕为EF.若菱形的边长
为2 cm,∠BAD=120°,则EF的长为 .
13.如图,已知矩形ABCD中,AB=8 cm,AD=10 cm,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的面积等于________cm2.
14.把两张宽为2 cm的矩形纸片重叠在一起,然后将其中的一张任意旋转一个角度,则重叠部分(图中的阴影部分)的四边形ABCD的形状为________,其面积的最小值为________cm2.
三、解答题
15.如图,已知在菱形ABCD中,点E、F分别为边CD、AD的中点,连接AE、CF。
求证:△ADE≌△CDF.
16.如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF是菱形.
17.如图在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
18.如图,在△ABC中,AB=AC,D是BC的中点,连接AD,在AD的延长线上取一点E,连接BE,CE.
(1)求证:△ABE≌△ACE;
(2)当AE与AD满足什么数量关系时,四边形ABEC是菱形?并说明理由.
参考答案
1.C
2.B
3.C
4.D
5.B
6.B
7.C.
8.C
9.答案为:AB=AD或AC⊥BD;
10.答案为:C;B=BF或BE⊥CF或∠EBF=60°或BD=BF(答案不唯一)
11.答案为:4.8;
12.答案为:(cm);
13.答案为:40
14.答案为:菱形,4
15.证明:∵四边形ABCD是菱形,∴AD=CD.
∵E、F分别是CD、AD的中点,∴DE=DC,DF=AD,∴DE=DF.
在△ADE和△CDF中,DE=DF,∠D=∠D,DA=DC∴△ADE≌△CDF(SAS).
16.证明:∵AF∥BC,∴∠EAF=∠ECD,∠EFA=∠EDC,
又∵E是AC的中点,∴AE=CE,∴△AEF≌△CED.∴AF=CD,
又AF∥CD,∴四边形ADCF是平行四边形.
∵AC=2AB,E为AC的中点,∴AE=AB,
由已知得∠EAD=∠BAD,又AD=AD,∴△AED≌△ABD.
∴∠AED=∠B=90°,即DF⊥AC.
∴四边形ADCF是菱形.
17.解:(1)证明:∵四边形ABCD是菱形,∴AB∥CD,AC⊥BD,∴AE∥CD,∠AOB=90°,
又∵DE⊥BD,即∠EDB=90°,∴∠AOB=∠EDB.∴DE∥AC.
∴四边形ACDE是平行四边形.
(2)∵四边形ABCD是菱形,AC=8,BD=6,∴AO=4,DO=3,∴AD=CD=5.
又∵四边形ACDE是平行四边形,∴AE=CD=5,DE=AC=8.
∴△ADE的周长为AD+AE+DE=5+5+8=18.
18.(1)证明:∵AB=AC,点D为BC的中点,∴∠BAE=∠CAE,
∵AE=AE∴△ABE≌△ACE(SAS).
(2)解:当AE=2AD(或AD=DE或DE=0.5AE)时,四边形ABEC是菱形
理由如下:∵AE=2AD,∴AD=DE,
又∵点D为BC中点,∴BD=CD,
∴四边形ABEC为平行四边形,
∵AB=AC,
∴四边形ABEC为菱形.
《菱形的性质与判定》课时练习
一、选择题
1.下列命题中错误的是( )
A.平行四边形的对角线互相平分
B.菱形的对角线互相垂直
C.同旁内角互补
D.矩形的对角线相等
2.平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-3,0),B(0,2),C(3,0),D(0,-2),则四边形ABCD是( )
A.矩形 B.菱形 C.正方形 D.梯形
3.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( )
A.28°???????? B.52°???????? C.62°???????? D.72°
4.菱形的两条对角线长分别是6和8,则此菱形的边长是( )
A.10 B.8 C.6 D.5
5.如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,
且∠CDF=24°,则∠DAB等于( )
??
A.100°???? ?? B.104°?? ??C.105°? ?? ??? ??D.110°
6.如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连结AE、EF、AF,则△AEF的周长为(???? )
A.? ? ? B.???? ??C.?? ? D.
7.某校的校园内有一个由两个相同的正六边形(边长为2.5m)围成的花坛,如图中的阴影部分所示,校方先要将这个花坛在原有的基础上扩建成一个菱形区域如图所示,并在新扩充的部分种上草坪,则扩建后菱形区域的周长为( )
A.20m? B.25m? C.30m? D.35m
8.如图,在菱形ABCD中,∠ABC=60°,AB=1,E为BC的中点,则对角线BD上的动点P到E、C两点的距离之和的最小值为( )
二、填空题
9.如图,如果要使平行四边形ABCD成为一个菱形,需要添加一个条件,那么你添加的条件是_________.
10.如图,两个完全相同的三角尺ABC和DEF在直线l上滑动.要使四边形CBFE为菱形,还需添加的一个条件是________(写出一个即可).
11.如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH=________.
12.如图,将菱形ABCD折叠,使点A恰好落在菱形的对角线交点O处,折痕为EF.若菱形的边长
为2 cm,∠BAD=120°,则EF的长为 .
13.如图,已知矩形ABCD中,AB=8 cm,AD=10 cm,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的面积等于________cm2.
14.把两张宽为2 cm的矩形纸片重叠在一起,然后将其中的一张任意旋转一个角度,则重叠部分(图中的阴影部分)的四边形ABCD的形状为________,其面积的最小值为________cm2.
三、解答题
15.如图,已知在菱形ABCD中,点E、F分别为边CD、AD的中点,连接AE、CF。
求证:△ADE≌△CDF.
16.如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF是菱形.
17.如图在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
18.如图,在△ABC中,AB=AC,D是BC的中点,连接AD,在AD的延长线上取一点E,连接BE,CE.
(1)求证:△ABE≌△ACE;
(2)当AE与AD满足什么数量关系时,四边形ABEC是菱形?并说明理由.
参考答案
1.C
2.B
3.C
4.D
5.B
6.B
7.C.
8.C
9.答案为:AB=AD或AC⊥BD;
10.答案为:C;B=BF或BE⊥CF或∠EBF=60°或BD=BF(答案不唯一)
11.答案为:4.8;
12.答案为:(cm);
13.答案为:40
14.答案为:菱形,4
15.证明:∵四边形ABCD是菱形,∴AD=CD.
∵E、F分别是CD、AD的中点,∴DE=DC,DF=AD,∴DE=DF.
在△ADE和△CDF中,DE=DF,∠D=∠D,DA=DC∴△ADE≌△CDF(SAS).
16.证明:∵AF∥BC,∴∠EAF=∠ECD,∠EFA=∠EDC,
又∵E是AC的中点,∴AE=CE,∴△AEF≌△CED.∴AF=CD,
又AF∥CD,∴四边形ADCF是平行四边形.
∵AC=2AB,E为AC的中点,∴AE=AB,
由已知得∠EAD=∠BAD,又AD=AD,∴△AED≌△ABD.
∴∠AED=∠B=90°,即DF⊥AC.
∴四边形ADCF是菱形.
17.解:(1)证明:∵四边形ABCD是菱形,∴AB∥CD,AC⊥BD,∴AE∥CD,∠AOB=90°,
又∵DE⊥BD,即∠EDB=90°,∴∠AOB=∠EDB.∴DE∥AC.
∴四边形ACDE是平行四边形.
(2)∵四边形ABCD是菱形,AC=8,BD=6,∴AO=4,DO=3,∴AD=CD=5.
又∵四边形ACDE是平行四边形,∴AE=CD=5,DE=AC=8.
∴△ADE的周长为AD+AE+DE=5+5+8=18.
18.(1)证明:∵AB=AC,点D为BC的中点,∴∠BAE=∠CAE,
∵AE=AE∴△ABE≌△ACE(SAS).
(2)解:当AE=2AD(或AD=DE或DE=0.5AE)时,四边形ABEC是菱形
理由如下:∵AE=2AD,∴AD=DE,
又∵点D为BC中点,∴BD=CD,
∴四边形ABEC为平行四边形,
∵AB=AC,
∴四边形ABEC为菱形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
