2021-2022学年北师大版九年级数学上册6.3 反比例函数的应用 同步测试题 (word版无答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册6.3 反比例函数的应用 同步测试题 (word版无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 115.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 19:53:42 | ||
图片预览

文档简介
10795000107569006.3 反比例函数的应用 同步测试题
(满分120分;时间:90分钟)
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , ) ?
1. 某人用所带的钱去买某种每枝售价1.8元的圆珠笔,恰好买12枝,假设他用这些钱可买单价为x元的圆珠笔y枝,那么y与x的函数关系式为(? ? ? ? ).
A.y=216x B.y=2.16x C.y=21.6x D.y=1.8x?
2. 一定质量的干松木,当它的体积V=2m3时,它的密度ρ=0.5×103kg/m3,则ρ与V的函数关系式是( )
A.ρ=1000V B.ρ=V+1000 C.ρ=500V D.ρ=1000V
3. 在平面直角坐标系中,直线y=?43x+8与x轴,y轴分别相交于A,B两点,与反比例函数y=kx在第一象限内的图象相交于点C,D两点.若CD=5,则k的值为( )
A.4.5 B.9 C.12 D.6?
4. 购买x斤水果需24元,购买一斤水果的单价y与x的关系式是( )
A.y=24x(x>0) B.y=24x(x为自然数)
C.y=24x(x为整数) D.y=24x(x为正整数)?
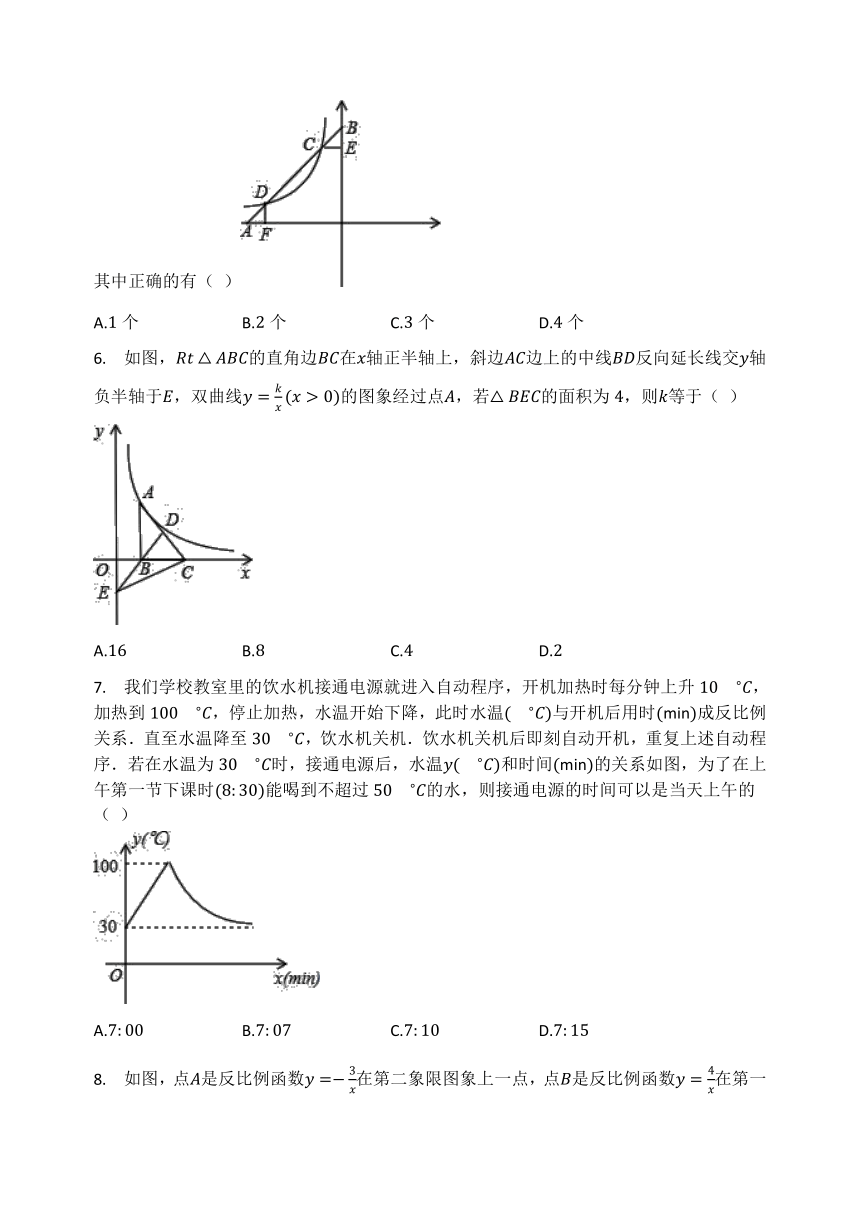
5. 如图,直线y1=x+b与x轴、y轴分别交于A,B两点,与反比例函数y2=?5x(x<0)交于C,D两点,点C的横坐标为?1,过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.下列说法:①b=6;②BC=AD;③五边形CDFOE的面积为35;④当xy2,其中正确的有( )
A.1个 B.2个 C.3个 D.4个?
6. 如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD反向延长线交y轴负半轴于E,双曲线y=kx(x>0)的图象经过点A,若△BEC的面积为4,则k等于( )
A.16 B.8 C.4 D.2?
7. 我们学校教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10??C,加热到100??C,停止加热,水温开始下降,此时水温(??C)与开机后用时(min)成反比例关系.直至水温降至30??C,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30??C时,接通电源后,水温y(??C)和时间(min)的关系如图,为了在上午第一节下课时(8:30)能喝到不超过50??C的水,则接通电源的时间可以是当天上午的( )
A.7:00 B.7:07 C.7:10 D.7:15
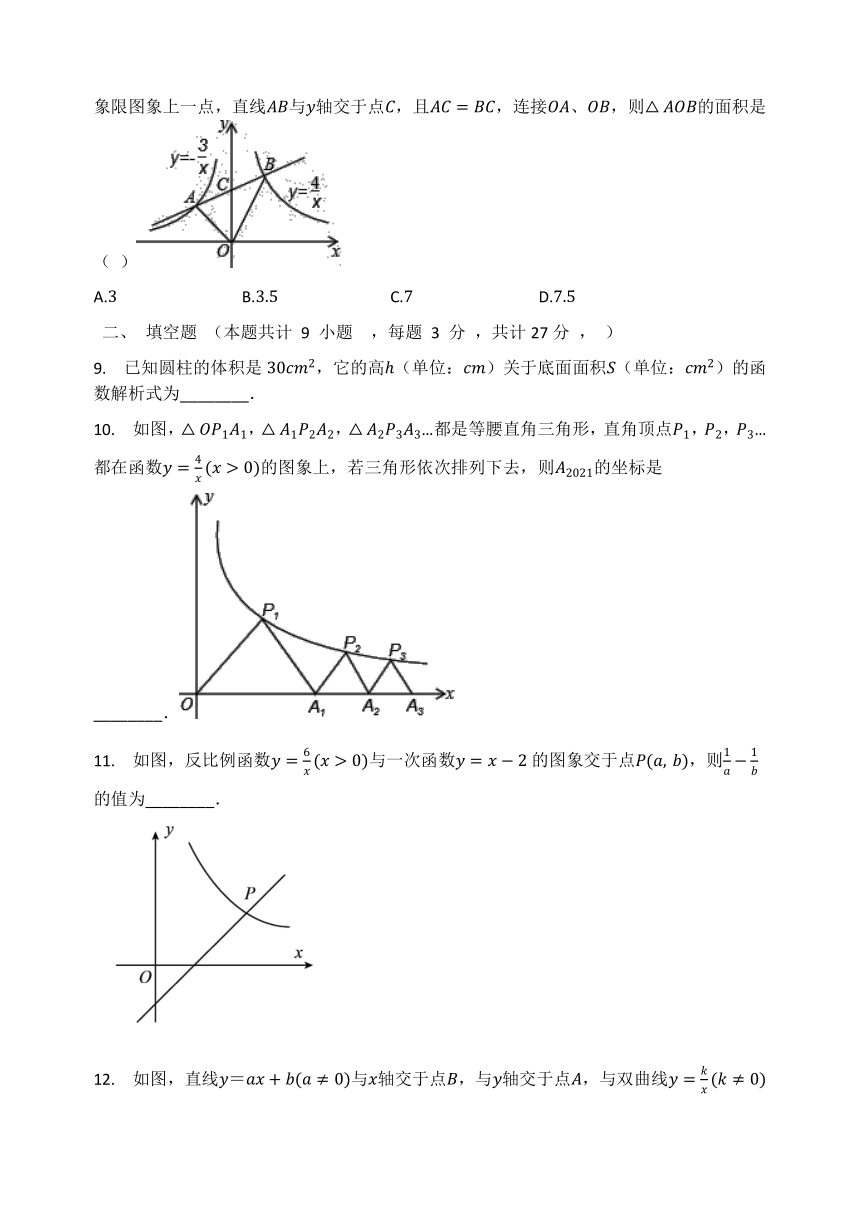
8. 如图,点A是反比例函数y=?3x在第二象限图象上一点,点B是反比例函数y=4x在第一象限图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,则△AOB的面积是( )
A.3 B.3.5 C.7 D.7.5
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , ) ?
9. 已知圆柱的体积是30cm2,它的高?(单位:cm)关于底面面积S(单位:cm2)的函数解析式为________. ?
10. 如图,△OP1A1,△A1P2A2,△A2P3A3…都是等腰直角三角形,直角顶点P1,P2,P3…都在函数y=4x(x>0)的图象上,若三角形依次排列下去,则A2021的坐标是________. ?
11. 如图,反比例函数y=6x(x>0)与一次函数y=x?2的图象交于点P(a,?b),则1a?1b的值为________.
?
12. 如图,直线y=ax+b(a≠0)与x轴交于点B,与y轴交于点A,与双曲线y=kx(k≠0)交于点C,若AB=BC,△AOC的面积为4,则k的值是________.
?
13. 甲、乙两地相距100km,如果一辆汽车从甲地到乙地所用时问为x(?),汽车行驶的平均速度为y(km/?),那么y与x之间的函数关系式为________ (不要求写出自变量的取值范围). ?
14. 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,?0),∠AOB=60?,点A在第一象限,过点A的双曲线为y=kx.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O'B'.当点O'与点A重合时,点P的坐标是________. ?
15. 如图,一块砖的A,B,C三个面的面积之比是4:2:1,如果把砖的A面向下放在地上时地面所受的压强为a,则把砖的B面和C面分别向下放在地上,地面所受压强分别为________. ?
16. 一定质量的二氧化碳,它的密度ρ(kg/m3)是它体积V(m3)的反比例函数,当V=5m3时,ρ=1.98kg/m3;则当V=10m3时,ρ=________kg/m3. ?
17. 采用药熏消毒法进行消毒,已知药物燃烧时室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧完后,y与x成反比例(如图所示).现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克.请根题中所提供的信息,解答下列问题:①药物燃烧时y关于x的函数关系式为:________,自变量x的取值范围是:________;药物燃烧后y关于x的函数关系式为:________,自变量x的取值范围是:________.②研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过________分钟后,学生才能回到教室.
三、 解答题 (本题共计 6 小题 ,共计69分 , ) ?
18. 某地上年度电价为0.8元,年用电量为1亿度,本年度计划将电价调至0.55?0.75元之间,经测算,若电价调至x元,则本年度新增电量y(亿度)与(x?0.4)成反比例,又当x=0.65元时,y=0.8.求:
(1)y与x之间的函数关系式;
(2)若电价调至0.6元时,本年度的用电量是多少?
?
19. 某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x元与日销售量y个之间有如下关系:
x?(元)
3
4
5
6
y?(个)
20
15
12
10
①请你认真分析表中数据,从你所学习过的一次函数、反比例函数和其它函数中确定哪种函数能表示其变化规律,说明确定是这种函数而不是其它函数的理由,并求出它的解析式;
②设经营此贺卡的销售利润为W元,试求出W(元)与x(元)之间的函数关系式.若物价局规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润?
?
20. 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的
正半轴上,点A在反比例函数y=kx(x>0)的图象上,点D的坐标为(4,?3).
(1)求k的值.
(2)若将菱形ABCD向右平移,使点D落在反比例函数y=kx(x>0)的图象上,求菱形ABCD平移的距离.
(3)怎样平移可以使点B、D同时落在第一象限的曲线上?
?
21. 如图,等腰梯形ABCD放置在平面坐标系中,已知A(?2,?0)、B(6,?0)、D(0,?3),反比例函数的图象经过点C.
(1)求点C的坐标和反比例函数的解析式;
(2)将等腰梯形ABCD向上平移2个单位后,问点B是否落在双曲线上?
?
22. 如图,一次函数y=ax+b的图象与反比例函数y=的图象交于M(2,?m),N(?1,??4)两点.
(1)求这两个函数的解析式.
(2)根据图象写出在第一象限使反比例函数值小于一次函数值x的取值范围.
?
23. 为预防“甲型H1N1”流感,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
(1)求药物燃烧时和药物燃烧后y与x的函数关系式及自变量的取值范围.
(2)当每立方米空气中含药量不低于2mg时,消毒有效,求这次有效消毒时间.
(3)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从燃烧开始,经多长时间学生才可以回教室?
(满分120分;时间:90分钟)
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , ) ?
1. 某人用所带的钱去买某种每枝售价1.8元的圆珠笔,恰好买12枝,假设他用这些钱可买单价为x元的圆珠笔y枝,那么y与x的函数关系式为(? ? ? ? ).
A.y=216x B.y=2.16x C.y=21.6x D.y=1.8x?
2. 一定质量的干松木,当它的体积V=2m3时,它的密度ρ=0.5×103kg/m3,则ρ与V的函数关系式是( )
A.ρ=1000V B.ρ=V+1000 C.ρ=500V D.ρ=1000V
3. 在平面直角坐标系中,直线y=?43x+8与x轴,y轴分别相交于A,B两点,与反比例函数y=kx在第一象限内的图象相交于点C,D两点.若CD=5,则k的值为( )
A.4.5 B.9 C.12 D.6?
4. 购买x斤水果需24元,购买一斤水果的单价y与x的关系式是( )
A.y=24x(x>0) B.y=24x(x为自然数)
C.y=24x(x为整数) D.y=24x(x为正整数)?
5. 如图,直线y1=x+b与x轴、y轴分别交于A,B两点,与反比例函数y2=?5x(x<0)交于C,D两点,点C的横坐标为?1,过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.下列说法:①b=6;②BC=AD;③五边形CDFOE的面积为35;④当xy2,其中正确的有( )
A.1个 B.2个 C.3个 D.4个?
6. 如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD反向延长线交y轴负半轴于E,双曲线y=kx(x>0)的图象经过点A,若△BEC的面积为4,则k等于( )
A.16 B.8 C.4 D.2?
7. 我们学校教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10??C,加热到100??C,停止加热,水温开始下降,此时水温(??C)与开机后用时(min)成反比例关系.直至水温降至30??C,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30??C时,接通电源后,水温y(??C)和时间(min)的关系如图,为了在上午第一节下课时(8:30)能喝到不超过50??C的水,则接通电源的时间可以是当天上午的( )
A.7:00 B.7:07 C.7:10 D.7:15
8. 如图,点A是反比例函数y=?3x在第二象限图象上一点,点B是反比例函数y=4x在第一象限图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,则△AOB的面积是( )
A.3 B.3.5 C.7 D.7.5
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , ) ?
9. 已知圆柱的体积是30cm2,它的高?(单位:cm)关于底面面积S(单位:cm2)的函数解析式为________. ?
10. 如图,△OP1A1,△A1P2A2,△A2P3A3…都是等腰直角三角形,直角顶点P1,P2,P3…都在函数y=4x(x>0)的图象上,若三角形依次排列下去,则A2021的坐标是________. ?
11. 如图,反比例函数y=6x(x>0)与一次函数y=x?2的图象交于点P(a,?b),则1a?1b的值为________.
?
12. 如图,直线y=ax+b(a≠0)与x轴交于点B,与y轴交于点A,与双曲线y=kx(k≠0)交于点C,若AB=BC,△AOC的面积为4,则k的值是________.
?
13. 甲、乙两地相距100km,如果一辆汽车从甲地到乙地所用时问为x(?),汽车行驶的平均速度为y(km/?),那么y与x之间的函数关系式为________ (不要求写出自变量的取值范围). ?
14. 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,?0),∠AOB=60?,点A在第一象限,过点A的双曲线为y=kx.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O'B'.当点O'与点A重合时,点P的坐标是________. ?
15. 如图,一块砖的A,B,C三个面的面积之比是4:2:1,如果把砖的A面向下放在地上时地面所受的压强为a,则把砖的B面和C面分别向下放在地上,地面所受压强分别为________. ?
16. 一定质量的二氧化碳,它的密度ρ(kg/m3)是它体积V(m3)的反比例函数,当V=5m3时,ρ=1.98kg/m3;则当V=10m3时,ρ=________kg/m3. ?
17. 采用药熏消毒法进行消毒,已知药物燃烧时室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧完后,y与x成反比例(如图所示).现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克.请根题中所提供的信息,解答下列问题:①药物燃烧时y关于x的函数关系式为:________,自变量x的取值范围是:________;药物燃烧后y关于x的函数关系式为:________,自变量x的取值范围是:________.②研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过________分钟后,学生才能回到教室.
三、 解答题 (本题共计 6 小题 ,共计69分 , ) ?
18. 某地上年度电价为0.8元,年用电量为1亿度,本年度计划将电价调至0.55?0.75元之间,经测算,若电价调至x元,则本年度新增电量y(亿度)与(x?0.4)成反比例,又当x=0.65元时,y=0.8.求:
(1)y与x之间的函数关系式;
(2)若电价调至0.6元时,本年度的用电量是多少?
?
19. 某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x元与日销售量y个之间有如下关系:
x?(元)
3
4
5
6
y?(个)
20
15
12
10
①请你认真分析表中数据,从你所学习过的一次函数、反比例函数和其它函数中确定哪种函数能表示其变化规律,说明确定是这种函数而不是其它函数的理由,并求出它的解析式;
②设经营此贺卡的销售利润为W元,试求出W(元)与x(元)之间的函数关系式.若物价局规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润?
?
20. 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的
正半轴上,点A在反比例函数y=kx(x>0)的图象上,点D的坐标为(4,?3).
(1)求k的值.
(2)若将菱形ABCD向右平移,使点D落在反比例函数y=kx(x>0)的图象上,求菱形ABCD平移的距离.
(3)怎样平移可以使点B、D同时落在第一象限的曲线上?
?
21. 如图,等腰梯形ABCD放置在平面坐标系中,已知A(?2,?0)、B(6,?0)、D(0,?3),反比例函数的图象经过点C.
(1)求点C的坐标和反比例函数的解析式;
(2)将等腰梯形ABCD向上平移2个单位后,问点B是否落在双曲线上?
?
22. 如图,一次函数y=ax+b的图象与反比例函数y=的图象交于M(2,?m),N(?1,??4)两点.
(1)求这两个函数的解析式.
(2)根据图象写出在第一象限使反比例函数值小于一次函数值x的取值范围.
?
23. 为预防“甲型H1N1”流感,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
(1)求药物燃烧时和药物燃烧后y与x的函数关系式及自变量的取值范围.
(2)当每立方米空气中含药量不低于2mg时,消毒有效,求这次有效消毒时间.
(3)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从燃烧开始,经多长时间学生才可以回教室?
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
