4.1函数的奇偶性(第二课时)课件(共32张PPT)——2021-2022学年高一上学期北师大版(2019)必修第一册
文档属性
| 名称 | 4.1函数的奇偶性(第二课时)课件(共32张PPT)——2021-2022学年高一上学期北师大版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-02 10:21:13 | ||
图片预览











文档简介
4.1函数的奇偶性
第二课时
教学目标
01
02
应用奇偶性定义求值、求解析式
03
应用奇偶性的定义求参
应用奇偶性的对称性
利用奇偶性求值和求解析式
重点
难点
整体奇偶与求参
环节一
奇偶性与对称性
考查对称性
角度一
例1.函数f(x)= ????????+???????? 的图象关于( )
A.原点对称 B.y轴对称
C.y=x 对称 D.y=-x 对称
?
解析:函数f(x)的定义域为{x|x≠0},关于原点对称.又f(-x)=(-x)3+1?????=-??3+1????=-f(x),所以f(x)是奇函数.故其图象关于原点对称.答案:A
?
例2.若函数????=????????为奇函数,则下列坐标表示的点一定在函数图像上的是( )
?
A.????,?????????
?
B.?????,??????????
?
C.?????,?????????
?
D.?????,??????????
?
解:(????,????????)在函数图像上,其关于原点对称的点?????,??????????也一定奇函数的图像上,因为奇函数的图像关于原点对称。
?
例3.(1)如果函数????=????????+????是偶函数,则????=????????的对称轴方程是什么?(2)函数????=?????????????是奇函数,则????=????????的中心是什么?
?
分析
????=????????+????的图像向右平移1个单位可得????=????????的图像.????=?????????????的图像向左平移1个单位可得????=????????的图像.
?
(1)由于函数????=????(????+1)是偶函数,其图像对称轴是y轴(x=0),平移后,????=????????的对称轴是????=????;
?
(2)由于函数????=????(????-1)是奇函数,其图像对称中心是(0,0)平移后,????=????????的中心(?????,????);
?
例4.定义在R上的奇函数f(x)在[0,+∞)上的图象如图所示,画出f(x)的图象。
解:先描出(1,1),(2,0)关于原点的对称点(-1,-1),(-2,0),连线可得f(x)的图象如图.
角度二
利用对称性补充图像
【启发】画图像前,先判断函数的奇偶性,可以画一半,对称出另一半。
角度三
利用对称性研究性质
例5.(1)已知奇函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示,求增区间。
3
1
解:?????,?????,?????,?????,????,????
?
角度三
利用对称性研究性质
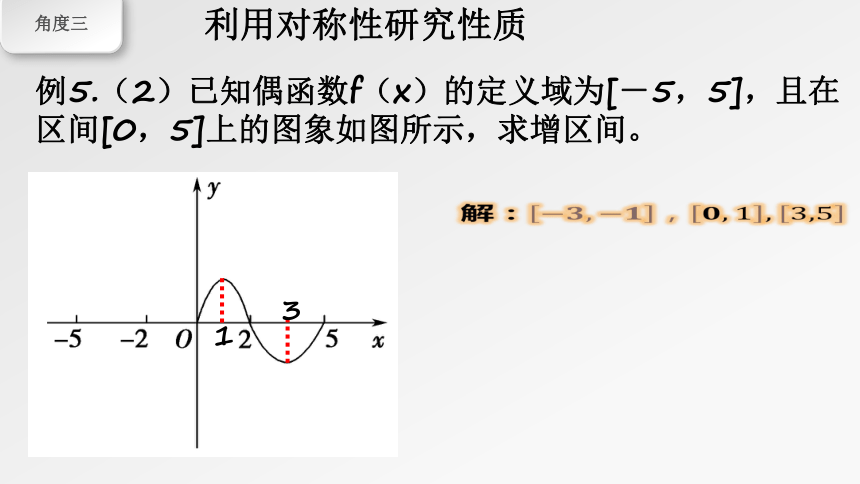
例5.(2)已知偶函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示,求增区间。
3
1
解:?????,?????,????,?????,????,????
?
点拨
1.设f(x)是偶函数,在区间????,????上是减(增)函数,则f????在区间?????,?????上是增(减)函数.
?
2.设f(x)是奇函数,在区间????,????上是减(增)函数,则f????在区间?????,?????上是减(增)函数.
?
奇同偶异
角度三
利用对称性研究性质
例6.已知f(x)是定义在区间[-2,0)∪(0,2]上的奇函数,当x>0时,f(x)的图象如图所示,则f(x)的值域是 .
解析:由题中图象可知,当x∈(0,2]时,2因为f(x)为奇函数,
所以当x∈[-2,0)时,有-3≤f(x)<-2,
所以函数f(x)的值域为[-3,-2)∪(2,3].
答案:[-3,-2)∪(2,3]
环节二
奇偶性求值
例7.已知f(x)是定义在R上的奇函数,则f(-1)+f(0)+f(1)=.
解析:∵f(x)是定义在R上的奇函数,
∴f(-1)=-f(1),f(0)=0,
∴f(-1)+f(0)+f(1)=-f(1)+0+f(1)=0.
答案:0
角度一
奇函数求值
例8.已知函数f(x)为奇函数,且当x>0时,f(x)=x2+1????,求f(-2)的值.
?
解:因为当x>0时,f(x)=x2+1????,
所以f(2)=22+12=92.又因为函数f(x)为奇函数,
所以f(-2)=-f(2)=-92.
?
角度一
奇函数求值
例9.已知偶函数f(x)满足f(x+2)=xf(x)(x∈R),则f(1)= .
解析:令x=-1,则f(-1+2)=-f(-1),
即f(1)=-f(-1).又f(x)为偶函数,
所以f(-1)=f(1),
所以f(1)=-f(1),得f(1)=0.
答案:0
角度二
偶函数求值
例10.设f(x)是定义在R上的偶函数,当x≤0时,f(x)=2x2-x,则f(1)等于( )
A.-3 B.-1 C.1 D.3
解析:∵f(x)是定义在R上的偶函数,且当x≤0时,f(x)=2x2-x,
∴f(1)=f(-1)=2·(-1)2-(-1)=2+1=3.
故选D.
角度二
偶函数求值
例11.已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x2+1,则f(1)+g(1)=( )
A.-3 B.-1 C.1 D.3
解析:把x=-1代入f(x)-g(x)=x3+x2+1,得f(-1)-g(-1)=1.
又f(x),g(x)分别是定义在R上的偶函数和奇函数,所以f(-1)-g(-1)=f(1)+g(1)=1.答案:C
角度三
奇偶函数联合求值
例12.已知f(x)=????????????+????????????+????????+????,????????=????,求?????????
?
解析:设????????=????????????+????????????+????????,则????????=????????+????且????????是R上奇 函数。
?
角度四
伪奇函数求值
则?????????=?????????+????且????????=????????+????,两式相加得:?????????+????????=????,∵ ????????=????,∴?????????=-5
?
环节三
奇偶性求解析式
例13.已知f(x)是定义在R上的奇函数,且当x>0时,f(x)=x(1-x),则当x<0时,f(x)=( )
A.-x(x-1) B.-x(x+1)
C.x(x-1) D.x(x+1)
角度一
奇函数求式
解析:设x<0,则-x>0,所以f(-x)=-x(1+x).
又f(x)为R上的奇函数,所以f(-x)=-f(x),
即-f(x)=-x(1+x),所以f(x)=x(1+x).
答案:D
先修改自变量
暂求?????????
?
归到????????
?
例14.已知函数f(x)是定义域为R的偶函数,且当x≥0时,f(x)=-x2+2x.求出函数f(x)在R上的解析式.
角度二
偶函数求式
解析:设x<0,则-x>0,所以f(-x)=-x2-2x.
又f(x)为R上的偶函数,所以f(-x)=f(x),
即f(x)=-x2-2x
先修改自变量
暂求?????????
?
归到????????
?
环节四
奇偶性求参
利用奇偶性求参数的常见类型及策略
(1)定义域含参数:奇(偶)函数f(x)的定义域为[a,b],根据定义域关于原点对称,利用a+b=0求参数.
(2)解析式含参数:根据f(-x)=-f(x)或f(-x)=f(x)列式,比较系数即可求解.
(3)奇函数在x=0处有意义时,一定有????????=????.
(4)偶函数在x=0处有意义时,未必有????????=????.
(5)偶函数有????????=?????????=????????
?
角度一
参数在定义域上
例15.如果定义在区间[2-a,4]上的函数f(x)为偶函数,那么a=
解析:因为函数f(x)为偶函数,所以函数的定义域关于原点对称,于是有2-a=-4,得a=6.
答案:6
角度二
参数在解析式上
例16.已知函数f(x)=(x+1)(x-a)为偶函数,求实数a的值
解:f(x)=(x+1)(x-a)=x2+(1-a)x-a.
因为函数f(x)是偶函数,所以1-a=0,得a=1.
角度二
参数在解析式上
例17.已知函数f(x)为定义在区间[-2,2]上的奇函数,当x∈[-2,0]时, f(x)=x2-????????x+a(a∈R).写出f(x)在区间[0,2]上的解析式;
?
解:f(x)为定义在区间[-2,2]上的奇函数,且f(x)在x=0处有意义,∴f(0)=0,即f(0)=a=0.∴a=0.
∴当x∈[-2,0]时,f(x)=x2-????????x.
设x∈[0,2],则-x∈[-2,0].
∴f(-x)=x2+????????x.
又∵f(-x)=-f(x),∴-f(x)=x2+????????x.
∴f(x)=-x2-????????x,x∈[0,2].
?
例18.已知函数f(x)=????????+????,????≤????,????????????+????????,????>???? 为奇函数,
则a+b= .?
?
解析:由题意知????(????)=?????(?????),????(????)=?????(?????),
则????????+????????=?????,????+????=????,解得????=?????,????=????.
当a=-1,b=1时,经检验知f(x)为奇函数,故a+b=0.
?
环节五
小结
课堂小结
1.核心要点
1.奇偶性与图像对称性;
2.求参求值求解析式
2.数学素养
体会数学抽象的过程,感受直观想象在解决问题中的应用,培养运算能力以及逻辑推理能力
谢谢观看
课件制作老师:胡琪
第二课时
教学目标
01
02
应用奇偶性定义求值、求解析式
03
应用奇偶性的定义求参
应用奇偶性的对称性
利用奇偶性求值和求解析式
重点
难点
整体奇偶与求参
环节一
奇偶性与对称性
考查对称性
角度一
例1.函数f(x)= ????????+???????? 的图象关于( )
A.原点对称 B.y轴对称
C.y=x 对称 D.y=-x 对称
?
解析:函数f(x)的定义域为{x|x≠0},关于原点对称.又f(-x)=(-x)3+1?????=-??3+1????=-f(x),所以f(x)是奇函数.故其图象关于原点对称.答案:A
?
例2.若函数????=????????为奇函数,则下列坐标表示的点一定在函数图像上的是( )
?
A.????,?????????
?
B.?????,??????????
?
C.?????,?????????
?
D.?????,??????????
?
解:(????,????????)在函数图像上,其关于原点对称的点?????,??????????也一定奇函数的图像上,因为奇函数的图像关于原点对称。
?
例3.(1)如果函数????=????????+????是偶函数,则????=????????的对称轴方程是什么?(2)函数????=?????????????是奇函数,则????=????????的中心是什么?
?
分析
????=????????+????的图像向右平移1个单位可得????=????????的图像.????=?????????????的图像向左平移1个单位可得????=????????的图像.
?
(1)由于函数????=????(????+1)是偶函数,其图像对称轴是y轴(x=0),平移后,????=????????的对称轴是????=????;
?
(2)由于函数????=????(????-1)是奇函数,其图像对称中心是(0,0)平移后,????=????????的中心(?????,????);
?
例4.定义在R上的奇函数f(x)在[0,+∞)上的图象如图所示,画出f(x)的图象。
解:先描出(1,1),(2,0)关于原点的对称点(-1,-1),(-2,0),连线可得f(x)的图象如图.
角度二
利用对称性补充图像
【启发】画图像前,先判断函数的奇偶性,可以画一半,对称出另一半。
角度三
利用对称性研究性质
例5.(1)已知奇函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示,求增区间。
3
1
解:?????,?????,?????,?????,????,????
?
角度三
利用对称性研究性质
例5.(2)已知偶函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示,求增区间。
3
1
解:?????,?????,????,?????,????,????
?
点拨
1.设f(x)是偶函数,在区间????,????上是减(增)函数,则f????在区间?????,?????上是增(减)函数.
?
2.设f(x)是奇函数,在区间????,????上是减(增)函数,则f????在区间?????,?????上是减(增)函数.
?
奇同偶异
角度三
利用对称性研究性质
例6.已知f(x)是定义在区间[-2,0)∪(0,2]上的奇函数,当x>0时,f(x)的图象如图所示,则f(x)的值域是 .
解析:由题中图象可知,当x∈(0,2]时,2
所以当x∈[-2,0)时,有-3≤f(x)<-2,
所以函数f(x)的值域为[-3,-2)∪(2,3].
答案:[-3,-2)∪(2,3]
环节二
奇偶性求值
例7.已知f(x)是定义在R上的奇函数,则f(-1)+f(0)+f(1)=.
解析:∵f(x)是定义在R上的奇函数,
∴f(-1)=-f(1),f(0)=0,
∴f(-1)+f(0)+f(1)=-f(1)+0+f(1)=0.
答案:0
角度一
奇函数求值
例8.已知函数f(x)为奇函数,且当x>0时,f(x)=x2+1????,求f(-2)的值.
?
解:因为当x>0时,f(x)=x2+1????,
所以f(2)=22+12=92.又因为函数f(x)为奇函数,
所以f(-2)=-f(2)=-92.
?
角度一
奇函数求值
例9.已知偶函数f(x)满足f(x+2)=xf(x)(x∈R),则f(1)= .
解析:令x=-1,则f(-1+2)=-f(-1),
即f(1)=-f(-1).又f(x)为偶函数,
所以f(-1)=f(1),
所以f(1)=-f(1),得f(1)=0.
答案:0
角度二
偶函数求值
例10.设f(x)是定义在R上的偶函数,当x≤0时,f(x)=2x2-x,则f(1)等于( )
A.-3 B.-1 C.1 D.3
解析:∵f(x)是定义在R上的偶函数,且当x≤0时,f(x)=2x2-x,
∴f(1)=f(-1)=2·(-1)2-(-1)=2+1=3.
故选D.
角度二
偶函数求值
例11.已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x2+1,则f(1)+g(1)=( )
A.-3 B.-1 C.1 D.3
解析:把x=-1代入f(x)-g(x)=x3+x2+1,得f(-1)-g(-1)=1.
又f(x),g(x)分别是定义在R上的偶函数和奇函数,所以f(-1)-g(-1)=f(1)+g(1)=1.答案:C
角度三
奇偶函数联合求值
例12.已知f(x)=????????????+????????????+????????+????,????????=????,求?????????
?
解析:设????????=????????????+????????????+????????,则????????=????????+????且????????是R上奇 函数。
?
角度四
伪奇函数求值
则?????????=?????????+????且????????=????????+????,两式相加得:?????????+????????=????,∵ ????????=????,∴?????????=-5
?
环节三
奇偶性求解析式
例13.已知f(x)是定义在R上的奇函数,且当x>0时,f(x)=x(1-x),则当x<0时,f(x)=( )
A.-x(x-1) B.-x(x+1)
C.x(x-1) D.x(x+1)
角度一
奇函数求式
解析:设x<0,则-x>0,所以f(-x)=-x(1+x).
又f(x)为R上的奇函数,所以f(-x)=-f(x),
即-f(x)=-x(1+x),所以f(x)=x(1+x).
答案:D
先修改自变量
暂求?????????
?
归到????????
?
例14.已知函数f(x)是定义域为R的偶函数,且当x≥0时,f(x)=-x2+2x.求出函数f(x)在R上的解析式.
角度二
偶函数求式
解析:设x<0,则-x>0,所以f(-x)=-x2-2x.
又f(x)为R上的偶函数,所以f(-x)=f(x),
即f(x)=-x2-2x
先修改自变量
暂求?????????
?
归到????????
?
环节四
奇偶性求参
利用奇偶性求参数的常见类型及策略
(1)定义域含参数:奇(偶)函数f(x)的定义域为[a,b],根据定义域关于原点对称,利用a+b=0求参数.
(2)解析式含参数:根据f(-x)=-f(x)或f(-x)=f(x)列式,比较系数即可求解.
(3)奇函数在x=0处有意义时,一定有????????=????.
(4)偶函数在x=0处有意义时,未必有????????=????.
(5)偶函数有????????=?????????=????????
?
角度一
参数在定义域上
例15.如果定义在区间[2-a,4]上的函数f(x)为偶函数,那么a=
解析:因为函数f(x)为偶函数,所以函数的定义域关于原点对称,于是有2-a=-4,得a=6.
答案:6
角度二
参数在解析式上
例16.已知函数f(x)=(x+1)(x-a)为偶函数,求实数a的值
解:f(x)=(x+1)(x-a)=x2+(1-a)x-a.
因为函数f(x)是偶函数,所以1-a=0,得a=1.
角度二
参数在解析式上
例17.已知函数f(x)为定义在区间[-2,2]上的奇函数,当x∈[-2,0]时, f(x)=x2-????????x+a(a∈R).写出f(x)在区间[0,2]上的解析式;
?
解:f(x)为定义在区间[-2,2]上的奇函数,且f(x)在x=0处有意义,∴f(0)=0,即f(0)=a=0.∴a=0.
∴当x∈[-2,0]时,f(x)=x2-????????x.
设x∈[0,2],则-x∈[-2,0].
∴f(-x)=x2+????????x.
又∵f(-x)=-f(x),∴-f(x)=x2+????????x.
∴f(x)=-x2-????????x,x∈[0,2].
?
例18.已知函数f(x)=????????+????,????≤????,????????????+????????,????>???? 为奇函数,
则a+b= .?
?
解析:由题意知????(????)=?????(?????),????(????)=?????(?????),
则????????+????????=?????,????+????=????,解得????=?????,????=????.
当a=-1,b=1时,经检验知f(x)为奇函数,故a+b=0.
?
环节五
小结
课堂小结
1.核心要点
1.奇偶性与图像对称性;
2.求参求值求解析式
2.数学素养
体会数学抽象的过程,感受直观想象在解决问题中的应用,培养运算能力以及逻辑推理能力
谢谢观看
课件制作老师:胡琪
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
