4.1函数的奇偶性(第三课时)课件(共35张PPT)-2021-2022学年高一上学期数学北师大版(2019)必修第一册
文档属性
| 名称 | 4.1函数的奇偶性(第三课时)课件(共35张PPT)-2021-2022学年高一上学期数学北师大版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-02 10:21:42 | ||
图片预览











文档简介
4.1函数的奇偶性
第三课时
教学目标
01
02
联合求值,特别是最值
03
联合解不等式、比较大小
单调性联合研究性质
奇偶性与单调性综合
奇偶性与单调性联合解不等式
重点
难点
函数具有隐性,如何挖掘
环节一
联合研究性质
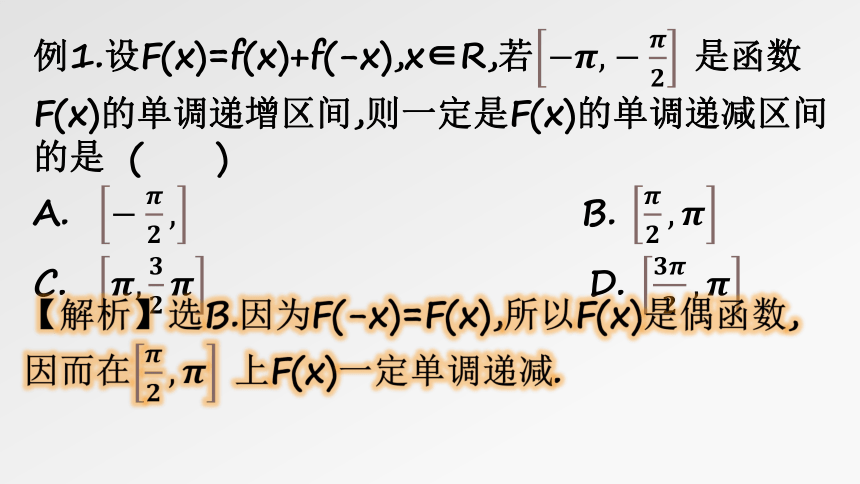
例1.设F(x)=f(x)+f(-x),x∈R,若?????,????????? 是函数F(x)的单调递增区间,则一定是F(x)的单调递减区间的是 ( )
A. ?????????
提示
1.设f(x)是偶函数,在区间????,????上是减(增)函数,则f????在区间?????,?????上是增(减)函数.
?
2.设f(x)是奇函数,在区间????,????上是减(增)函数,则f????在区间?????,?????上是减(增)函数.
?
奇同偶异
例1.设F(x)=f(x)+f(-x),x∈R,若?????,????????? 是函数F(x)的单调递增区间,则一定是F(x)的单调递减区间的是 ( )
A. ?????????
例2.设函数f(x)=x3- ???????? ,则f(x) ( )
A.是奇函数,且在(0,+∞)单调递增
B.是奇函数,且在(0,+∞)单调递减
C.是偶函数,且在(0,+∞)单调递增
D.是偶函数,且在(0,+∞)单调递减
?
【解析】选A.因为函数f(x) =x3- ???????? 的定义域为?
例3.已知函数f(x)是定义域为R的偶函数,且当x≥0时,f(x)=-x2+2x.
(1)求出函数f(x)在R上的解析式.
(2)画出函数f(x)的图象.
(3)根据图象,写出函数f(x)的单调递减区间
【解析】(1)因为函数f(x)是定义域为R的偶函数,
所以f(x)=f(-x).
当x<0时,-x>0,所以f(x)=f(-x)=-x2-2x.
综上,????????=?????????+
(2)函数f(x)的图象如图所示:
(3)由(2)中图象可知,f(x)的单调递减区间为[-1,0],[1,+∞)
例4.已知函数f(x)=(m-2)x2+(m2-4)x+m是偶函数,g(x)=-x2-mx在(-∞,0)内单调递增,则实数m= ( )
A.-2 B.±2 C.0 D.2
【解析】选A.由函数f(x)=(m-2)x2+(m2-4)x+m是偶函数,得m2-4=0.解得m=±2.
当m=2时,g(x)=-x2-2x,该函数在(-∞,0)内不单调递增,故m≠2.当m=-2时,g(x)=-x2+2x,该函数在(-∞,0)内单调递增,故m=-2.
环节二
联合求值
例5.已知奇函数f(x)在区间
环节三
联合解不等式
提示
1.这两个性质联合在一起解不等式,本质是脱法则,化不等式为代数不等式。需要以下两方面经验
经验一 ????,????2∈????↑+ fx1 ????,????2∈????↓+ fx1x2
经验二 要使用上述规则,要求:自变量同属一个单调区间;单调性已知;不等式标准。如果有一个因素不符合要求,就考虑用奇偶性辅助完成。
?
提示
2.【奇同】奇函数在对称区间上增减性相同。但要注意的是,两个区间是不是【统】的。例如y=1x在?∞,0,0,+∞上都是减函数,但使用时还需要区分对待,不可大统一。
?
3.【偶异】偶函数在对称区间上增减性相反。所以,两个区间是不会【统】的。这就给使用带来了麻烦,为了避免这个麻烦,我们发现偶函数有f?x=fx=fx,无论自变量正负,都可以通过加绝对值变成非负数,保证两个变量属同一区间。
?
角度一
奇偶性和增减性已知
例6.已知????????是R上奇函数且在????,+∞是增函数,????????
角度一
奇偶性和增减性已知
例7.函数f(x)是定义在实数集上的偶函数,且在[0,+∞)上单调递增,f(3)A.a>1 B.a<-2
C.a>1或a<-2 D.-1分析
三个要素:函数定义域R,单调性已知了一半,另一半需借助偶函数推导;两个自变量分布在同一增区间,还是一增一减区间,不明确;不等式是标准形态。
角度一
奇偶性和增减性已知
例7.函数f(x)是定义在实数集上的偶函数,且在[0,+∞)上单调递增,f(3)A.a>1 B.a<-2
C.a>1或a<-2 D.-1分析
需要解决的问题是:明确增减区间,控制两个自变量在同一单调区间内。
角度一
奇偶性和增减性已知
例7.函数f(x)是定义在实数集上的偶函数,且在[0,+∞)上单调递增,f(3)A.a>1 B.a<-2
C.a>1或a<-2 D.-1【解析】选C.因为函数f(x)在实数集上是偶函数,且f(3)所以3<|2a+1|,解得a>1或a<-2.
角度二
奇偶性和增减性隐含
例8.定义在R上偶函数????????满足:对?∞,
角度二
奇偶性和增减性隐含
例9.定义在R上奇函数????????满足:对上任意不相等的????????,????????,有????????????????????+????????????????????角度二
奇偶性和增减性隐含
例10.????????=????????????
特别提示
不要过分拘泥于【套用增减性脱f】,面对复杂的不等式,要善于【数形结合】,有的题也可以用【代入法】
角度三
代入法
例11.已知f(x)是定义域为R的偶函数,当x≥0时,f(x)=x2-4x,那么,不等式f(x+2)<5的解集是
分析
增减性不知,不等式不标准,是突出的两个问题。注意到????=????????,还注意到????≥
角度三
代入法
例11.已知f(x)是定义域为R的偶函数,当x≥0时,f(x)=x2-4x,那么,不等式f(x+2)<5的解集是
解:因为f(x)为偶函数,所以f(|x+2|)=f(x+2),则f(x+2)<5可化为f(|x+2|)<5,则|x+2|2-4|x+2|<5,
即(|x+2|+1)(|x+2|-5)<0,
所以|x+2|<5,解得-7所以不等式f(x+2)<5的解集是(-7,3).
角度四
数形结合
例12.已知f(x)是定义在?
环节四
联合比较大小
提示
????1????2∈????↑+????1>????2?f????1>f????2
?
????1????2∈????↓+????1>????2?f????1?
角度一
奇偶性和增减性已知
例13.定义在R上的偶函数f(x)在[0,+∞)上是增函数,若f(a)A.ab
C.|a|<|b| D.0≤ab≥0
[答案] C
角度一
奇偶性和增减性已知
微练.已知f(x)是定义在R上的偶函数,且有f(3)>f(1),则下列各式一定成立的是( )
A.f(-1)C.f(3)>f(2) D.f(2)>f(0)
解析:因为f(x)为偶函数,所以f(-1)=f(1).
又f(3)>f(1),所以f(3)>f(-1).
而B,C,D项中的各式大小关系不确定.
答案:A
角度二
奇偶性和增减性隐含
例14.定义在R上的奇函数f(x),且对任意实数a,b,????+
角度三
数形结合
例15. f(x)在
课堂小结
1.核心要点
联合性质:求值、解不等式、比较大小
2.数学素养
体会数学抽象的过程,感受直观想象在解决问题中的应用,培养运算能力以及逻辑推理能力
谢谢观看
第三课时
教学目标
01
02
联合求值,特别是最值
03
联合解不等式、比较大小
单调性联合研究性质
奇偶性与单调性综合
奇偶性与单调性联合解不等式
重点
难点
函数具有隐性,如何挖掘
环节一
联合研究性质
例1.设F(x)=f(x)+f(-x),x∈R,若?????,????????? 是函数F(x)的单调递增区间,则一定是F(x)的单调递减区间的是 ( )
A. ?????????
提示
1.设f(x)是偶函数,在区间????,????上是减(增)函数,则f????在区间?????,?????上是增(减)函数.
?
2.设f(x)是奇函数,在区间????,????上是减(增)函数,则f????在区间?????,?????上是减(增)函数.
?
奇同偶异
例1.设F(x)=f(x)+f(-x),x∈R,若?????,????????? 是函数F(x)的单调递增区间,则一定是F(x)的单调递减区间的是 ( )
A. ?????????
例2.设函数f(x)=x3- ???????? ,则f(x) ( )
A.是奇函数,且在(0,+∞)单调递增
B.是奇函数,且在(0,+∞)单调递减
C.是偶函数,且在(0,+∞)单调递增
D.是偶函数,且在(0,+∞)单调递减
?
【解析】选A.因为函数f(x) =x3- ???????? 的定义域为?
例3.已知函数f(x)是定义域为R的偶函数,且当x≥0时,f(x)=-x2+2x.
(1)求出函数f(x)在R上的解析式.
(2)画出函数f(x)的图象.
(3)根据图象,写出函数f(x)的单调递减区间
【解析】(1)因为函数f(x)是定义域为R的偶函数,
所以f(x)=f(-x).
当x<0时,-x>0,所以f(x)=f(-x)=-x2-2x.
综上,????????=?????????+
(2)函数f(x)的图象如图所示:
(3)由(2)中图象可知,f(x)的单调递减区间为[-1,0],[1,+∞)
例4.已知函数f(x)=(m-2)x2+(m2-4)x+m是偶函数,g(x)=-x2-mx在(-∞,0)内单调递增,则实数m= ( )
A.-2 B.±2 C.0 D.2
【解析】选A.由函数f(x)=(m-2)x2+(m2-4)x+m是偶函数,得m2-4=0.解得m=±2.
当m=2时,g(x)=-x2-2x,该函数在(-∞,0)内不单调递增,故m≠2.当m=-2时,g(x)=-x2+2x,该函数在(-∞,0)内单调递增,故m=-2.
环节二
联合求值
例5.已知奇函数f(x)在区间
环节三
联合解不等式
提示
1.这两个性质联合在一起解不等式,本质是脱法则,化不等式为代数不等式。需要以下两方面经验
经验一 ????,????2∈????↑+ fx1
经验二 要使用上述规则,要求:自变量同属一个单调区间;单调性已知;不等式标准。如果有一个因素不符合要求,就考虑用奇偶性辅助完成。
?
提示
2.【奇同】奇函数在对称区间上增减性相同。但要注意的是,两个区间是不是【统】的。例如y=1x在?∞,0,0,+∞上都是减函数,但使用时还需要区分对待,不可大统一。
?
3.【偶异】偶函数在对称区间上增减性相反。所以,两个区间是不会【统】的。这就给使用带来了麻烦,为了避免这个麻烦,我们发现偶函数有f?x=fx=fx,无论自变量正负,都可以通过加绝对值变成非负数,保证两个变量属同一区间。
?
角度一
奇偶性和增减性已知
例6.已知????????是R上奇函数且在????,+∞是增函数,????????
角度一
奇偶性和增减性已知
例7.函数f(x)是定义在实数集上的偶函数,且在[0,+∞)上单调递增,f(3)
C.a>1或a<-2 D.-1
三个要素:函数定义域R,单调性已知了一半,另一半需借助偶函数推导;两个自变量分布在同一增区间,还是一增一减区间,不明确;不等式是标准形态。
角度一
奇偶性和增减性已知
例7.函数f(x)是定义在实数集上的偶函数,且在[0,+∞)上单调递增,f(3)
C.a>1或a<-2 D.-1
需要解决的问题是:明确增减区间,控制两个自变量在同一单调区间内。
角度一
奇偶性和增减性已知
例7.函数f(x)是定义在实数集上的偶函数,且在[0,+∞)上单调递增,f(3)
C.a>1或a<-2 D.-1
角度二
奇偶性和增减性隐含
例8.定义在R上偶函数????????满足:对?∞,
角度二
奇偶性和增减性隐含
例9.定义在R上奇函数????????满足:对上任意不相等的????????,????????,有????????????????????+????????????????????角度二
奇偶性和增减性隐含
例10.????????=????????????
特别提示
不要过分拘泥于【套用增减性脱f】,面对复杂的不等式,要善于【数形结合】,有的题也可以用【代入法】
角度三
代入法
例11.已知f(x)是定义域为R的偶函数,当x≥0时,f(x)=x2-4x,那么,不等式f(x+2)<5的解集是
分析
增减性不知,不等式不标准,是突出的两个问题。注意到????=????????,还注意到????≥
角度三
代入法
例11.已知f(x)是定义域为R的偶函数,当x≥0时,f(x)=x2-4x,那么,不等式f(x+2)<5的解集是
解:因为f(x)为偶函数,所以f(|x+2|)=f(x+2),则f(x+2)<5可化为f(|x+2|)<5,则|x+2|2-4|x+2|<5,
即(|x+2|+1)(|x+2|-5)<0,
所以|x+2|<5,解得-7
角度四
数形结合
例12.已知f(x)是定义在?
环节四
联合比较大小
提示
????1????2∈????↑+????1>????2?f????1>f????2
?
????1????2∈????↓+????1>????2?f????1
角度一
奇偶性和增减性已知
例13.定义在R上的偶函数f(x)在[0,+∞)上是增函数,若f(a)
C.|a|<|b| D.0≤a
[答案] C
角度一
奇偶性和增减性已知
微练.已知f(x)是定义在R上的偶函数,且有f(3)>f(1),则下列各式一定成立的是( )
A.f(-1)
解析:因为f(x)为偶函数,所以f(-1)=f(1).
又f(3)>f(1),所以f(3)>f(-1).
而B,C,D项中的各式大小关系不确定.
答案:A
角度二
奇偶性和增减性隐含
例14.定义在R上的奇函数f(x),且对任意实数a,b,????+
角度三
数形结合
例15. f(x)在
课堂小结
1.核心要点
联合性质:求值、解不等式、比较大小
2.数学素养
体会数学抽象的过程,感受直观想象在解决问题中的应用,培养运算能力以及逻辑推理能力
谢谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
