7.1.1条件概率课件-2020-2021学年高二下学期数学人教A版(2019)选择性必修第三册(29张PPT)
文档属性
| 名称 | 7.1.1条件概率课件-2020-2021学年高二下学期数学人教A版(2019)选择性必修第三册(29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 957.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-02 00:00:00 | ||
图片预览



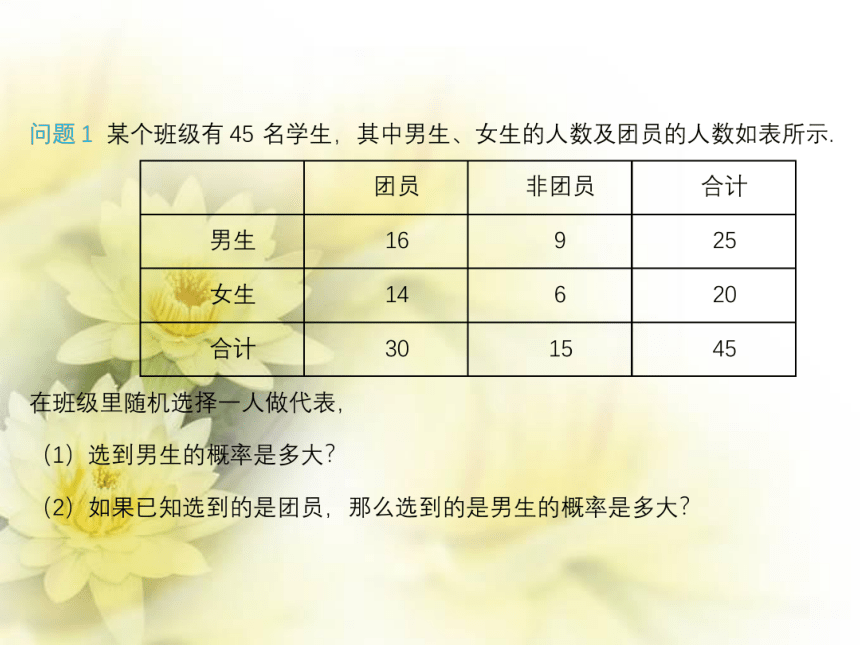





文档简介
7.1.1条件概率
第七章 随机变量及其分布列
学习目标
1.结合古典概型,了解条件概率的概念,能计算简单随机事件的条件概率.
2.结合古典概型,了解条件概率与事件的独立性的关系.
3.结合古典概型,会利用乘法公式计算概率.
思考
条件概率
条件概率与事件相互独立性的关系
概率的乘法公式
条件概率公式与乘法公式的应用
例1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回. 求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
分析:如果把“第1次抽到代数题”和“第2次抽到几何题”作为两个事件,那么问题(1)就是积事件的概率,问题(2)就是条件概率. 可以先求积事件的概率,再用条件概率公式求条件概率;也可以先求条件概率,再用乘法公式求积事件的概率.
例2 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次无放回地各抽一张. 他们中奖的概率与抽奖的次序有关吗?
分析:要知道中奖概率是否与抽奖次序有关,只要考察甲、乙、丙3名同学的中奖概率是否相等. 因为只有1张有奖,所以“乙中奖”等价于“甲没中奖且乙中奖”,“丙中奖”等价于“甲和乙都没中奖”,利用乘法公式可求出乙、丙中奖的概率.
事实上,在抽奖问题中,无论是放回还是不放回随机抽取,中奖的概率都与抽奖的次序无关.
课堂小练
5.某地一农业科技实验站,对一批新水稻种子进行试验,已知这批水稻种子的发芽率为0.8,发出芽后的幼苗成活率为0.9,在这批水稻种子中,随机地抽取一粒,则这粒水稻种子能成长为幼苗的概率为( )
A.0.02 B.0.08 C.0.18 D.0.72
课堂小结
——你学到了那些新知识呢?
本节课学习了条件概率、
乘法公式及其应用.
谢谢观看!
第七章 随机变量及其分布列
学习目标
1.结合古典概型,了解条件概率的概念,能计算简单随机事件的条件概率.
2.结合古典概型,了解条件概率与事件的独立性的关系.
3.结合古典概型,会利用乘法公式计算概率.
思考
条件概率
条件概率与事件相互独立性的关系
概率的乘法公式
条件概率公式与乘法公式的应用
例1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回. 求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
分析:如果把“第1次抽到代数题”和“第2次抽到几何题”作为两个事件,那么问题(1)就是积事件的概率,问题(2)就是条件概率. 可以先求积事件的概率,再用条件概率公式求条件概率;也可以先求条件概率,再用乘法公式求积事件的概率.
例2 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次无放回地各抽一张. 他们中奖的概率与抽奖的次序有关吗?
分析:要知道中奖概率是否与抽奖次序有关,只要考察甲、乙、丙3名同学的中奖概率是否相等. 因为只有1张有奖,所以“乙中奖”等价于“甲没中奖且乙中奖”,“丙中奖”等价于“甲和乙都没中奖”,利用乘法公式可求出乙、丙中奖的概率.
事实上,在抽奖问题中,无论是放回还是不放回随机抽取,中奖的概率都与抽奖的次序无关.
课堂小练
5.某地一农业科技实验站,对一批新水稻种子进行试验,已知这批水稻种子的发芽率为0.8,发出芽后的幼苗成活率为0.9,在这批水稻种子中,随机地抽取一粒,则这粒水稻种子能成长为幼苗的概率为( )
A.0.02 B.0.08 C.0.18 D.0.72
课堂小结
——你学到了那些新知识呢?
本节课学习了条件概率、
乘法公式及其应用.
谢谢观看!
