7.5正态分布课件-2020-2021学年高二下学期数学人教A版(2019)选择性必修第三册(24张PPT)
文档属性
| 名称 | 7.5正态分布课件-2020-2021学年高二下学期数学人教A版(2019)选择性必修第三册(24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-02 10:28:33 | ||
图片预览







文档简介
7.5 正态分布
第七章 随机变量及其分布
学习目标:
1. 通过具体实例,了解服从正态分布的随机变量,借助频率分布直方图的几何直观,了解正态分布的特征;
2. 能够根据正态曲线的特点求随机变量在某一区间内的概率;
3. 了解正态分布的均值、方差及其含义,会用正态分布解决实际问题.
教学重点:
正态分布的意义和特点.
教学难点:
借助正态分布密度曲线的对称性,利用数形结合求解正态分布的问题.
除了前面已经研究过的离散型随机变量外,还有大量问题中的随机变量不是离散型的,它们的取值往往充满某个区间甚至整个实轴,但取一点的概率为0,我们称这类随机变量为连续型随机变量.
问题1 自动流水线包装的食盐,每袋标准质量为400g.由于各种不可控制的因素,任意抽取一袋食盐,它的质量与标准质量之间或多或少会存在一定的误差(实际质量减去标准质量).用X表示这种误差,则X是一个连续型随机变量.检测人员在一次产品检验中,随机抽取了100袋食盐,获得误差X(单位:g)的观测值如下:
(1)如何描述这100个样本误差数据的分布?
(2)如何构建适当的概率模型刻画误差X的分布?
根据已学的统计知识,可用频率分布直方图描述这组误差数据的分布,如下图所示.频率分布直方图中每个小矩形的面积表示误差落在相应区间内的频率,所有小矩形的面积之和为1.
观察图形可知:误差观测值有正有负,并大致对称地分布在X=0的两侧,而且小误差比大误差出现得更频繁.
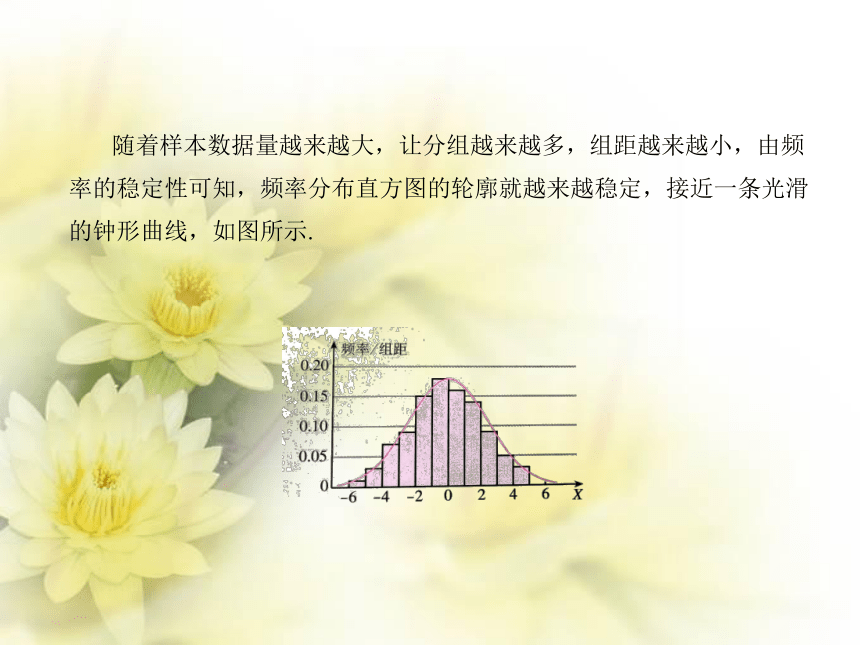
随着样本数据量越来越大,让分组越来越多,组距越来越小,由频率的稳定性可知,频率分布直方图的轮廓就越来越稳定,接近一条光滑的钟形曲线,如图所示.
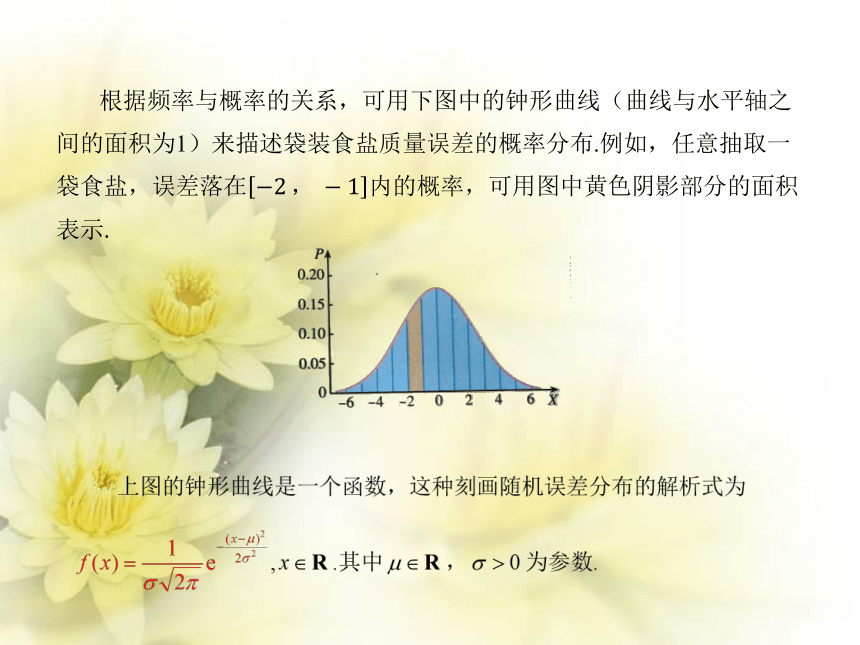
根据频率与概率的关系,可用下图中的钟形曲线(曲线与水平轴之间的面积为1)来描述袋装食盐质量误差的概率分布.例如,任意抽取一袋食盐,误差落在?2?,??1内的概率,可用图中黄色阴影部分的面积表示.
?
例 李明上学有时坐公交车,有时骑自行车. 他各记录了50次坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30 min,样本方差为36;骑自行车平均用时34 min,样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布.
(1)估计X,Y的分布中的参数;
(2)根据(1)中的估计结果,利用信息技术工具画出X和Y的分布密度曲线;
(3)如果某天有38 min可用,李明应选择哪种交通工具?如果某天只有34 min可用,又应该选择哪种交通工具?请说明理由.
(2)X和Y的分布密度曲线如图所示.
练一练
A
练一练
C
练一练
C
练一练
0.954
练一练
练一练
课堂小结
——你学到了那些新知识呢?
1. 正态密度函数与正态分布;
2. 正态分布的特点与性质.
3. 正态分布的3????原则.
第七章 随机变量及其分布
学习目标:
1. 通过具体实例,了解服从正态分布的随机变量,借助频率分布直方图的几何直观,了解正态分布的特征;
2. 能够根据正态曲线的特点求随机变量在某一区间内的概率;
3. 了解正态分布的均值、方差及其含义,会用正态分布解决实际问题.
教学重点:
正态分布的意义和特点.
教学难点:
借助正态分布密度曲线的对称性,利用数形结合求解正态分布的问题.
除了前面已经研究过的离散型随机变量外,还有大量问题中的随机变量不是离散型的,它们的取值往往充满某个区间甚至整个实轴,但取一点的概率为0,我们称这类随机变量为连续型随机变量.
问题1 自动流水线包装的食盐,每袋标准质量为400g.由于各种不可控制的因素,任意抽取一袋食盐,它的质量与标准质量之间或多或少会存在一定的误差(实际质量减去标准质量).用X表示这种误差,则X是一个连续型随机变量.检测人员在一次产品检验中,随机抽取了100袋食盐,获得误差X(单位:g)的观测值如下:
(1)如何描述这100个样本误差数据的分布?
(2)如何构建适当的概率模型刻画误差X的分布?
根据已学的统计知识,可用频率分布直方图描述这组误差数据的分布,如下图所示.频率分布直方图中每个小矩形的面积表示误差落在相应区间内的频率,所有小矩形的面积之和为1.
观察图形可知:误差观测值有正有负,并大致对称地分布在X=0的两侧,而且小误差比大误差出现得更频繁.
随着样本数据量越来越大,让分组越来越多,组距越来越小,由频率的稳定性可知,频率分布直方图的轮廓就越来越稳定,接近一条光滑的钟形曲线,如图所示.
根据频率与概率的关系,可用下图中的钟形曲线(曲线与水平轴之间的面积为1)来描述袋装食盐质量误差的概率分布.例如,任意抽取一袋食盐,误差落在?2?,??1内的概率,可用图中黄色阴影部分的面积表示.
?
例 李明上学有时坐公交车,有时骑自行车. 他各记录了50次坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30 min,样本方差为36;骑自行车平均用时34 min,样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布.
(1)估计X,Y的分布中的参数;
(2)根据(1)中的估计结果,利用信息技术工具画出X和Y的分布密度曲线;
(3)如果某天有38 min可用,李明应选择哪种交通工具?如果某天只有34 min可用,又应该选择哪种交通工具?请说明理由.
(2)X和Y的分布密度曲线如图所示.
练一练
A
练一练
C
练一练
C
练一练
0.954
练一练
练一练
课堂小结
——你学到了那些新知识呢?
1. 正态密度函数与正态分布;
2. 正态分布的特点与性质.
3. 正态分布的3????原则.
