2020-2021学年湖南省娄底市新化县八年级(下)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年湖南省娄底市新化县八年级(下)期末数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 945.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-02 00:00:00 | ||
图片预览

文档简介
2020-2021学年湖南省娄底市新化县八年级(下)期末数学试卷
一、选择题(本大题共12小题,每小题3分,满分36分,请将正确答案的序号填在答题卡上)
1.在△ABC中,已知AB=5,AC=12,BC=13,则该三角形为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形.
2.小明3分钟共投篮80次,进了50个球,则小明进球的频率是( )
A.80 B.50 C.1.6 D.0.625
3.下列函数中,自变量x的取值范围是x≥3的是( )
A.y= B.y= C.y=x﹣3 D.y=
4.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
5.下列命题中,错误的是( )
A.平行四边形的对角线互相平分
B.菱形的对角线互相垂直平分
C.矩形的对角线相等且互相垂直平分
D.角平分线上的点到角两边的距离相等
6.如图,OA是∠BAC的平分线,OM⊥AC于点M,ON⊥AB于点N,若ON=8cm,则OM长为( )
A.4cm B.5cm C.8cm D.20cm
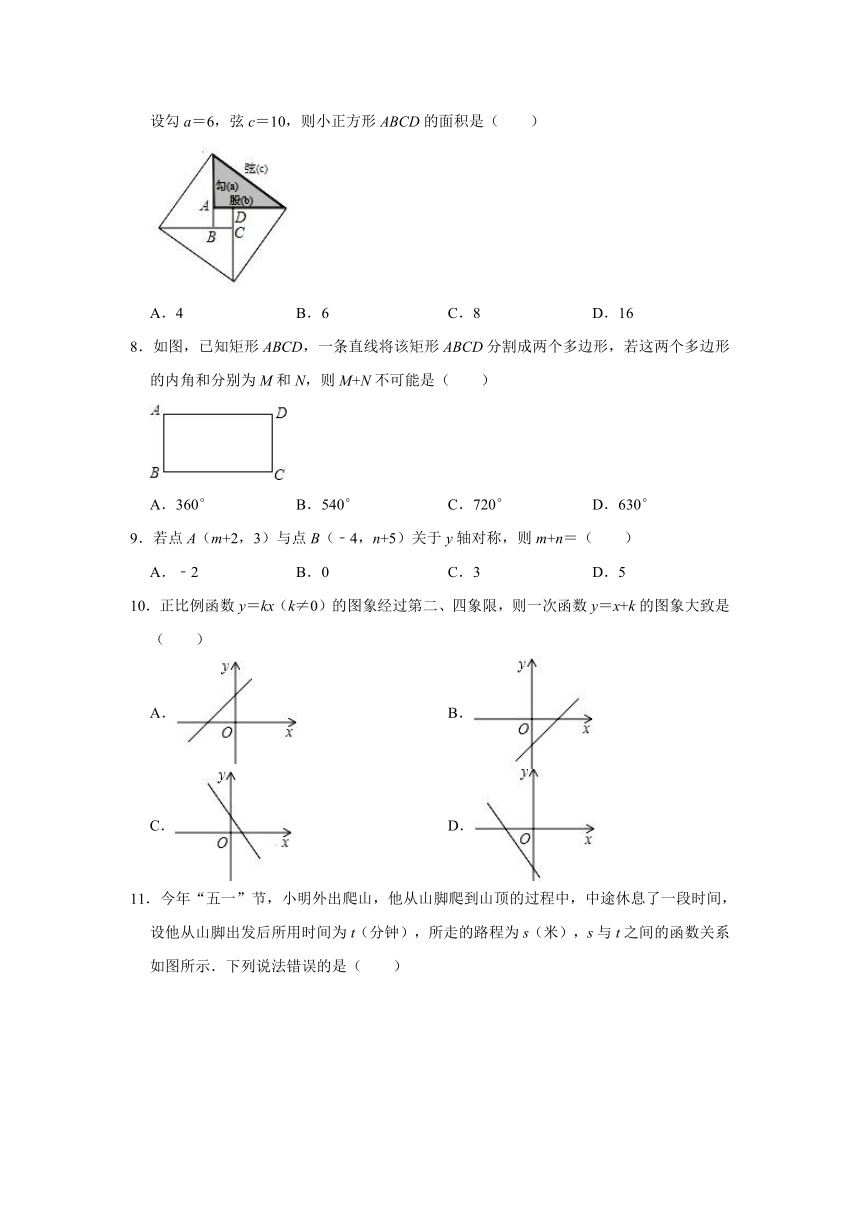
7.公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是( )
A.4 B.6 C.8 D.16
8.如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,若这两个多边形的内角和分别为M和N,则M+N不可能是( )
A.360° B.540° C.720° D.630°
9.若点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,则m+n=( )
A.﹣2 B.0 C.3 D.5
10.正比例函数y=kx(k≠0)的图象经过第二、四象限,则一次函数y=x+k的图象大致是( )
A. B.
C. D.
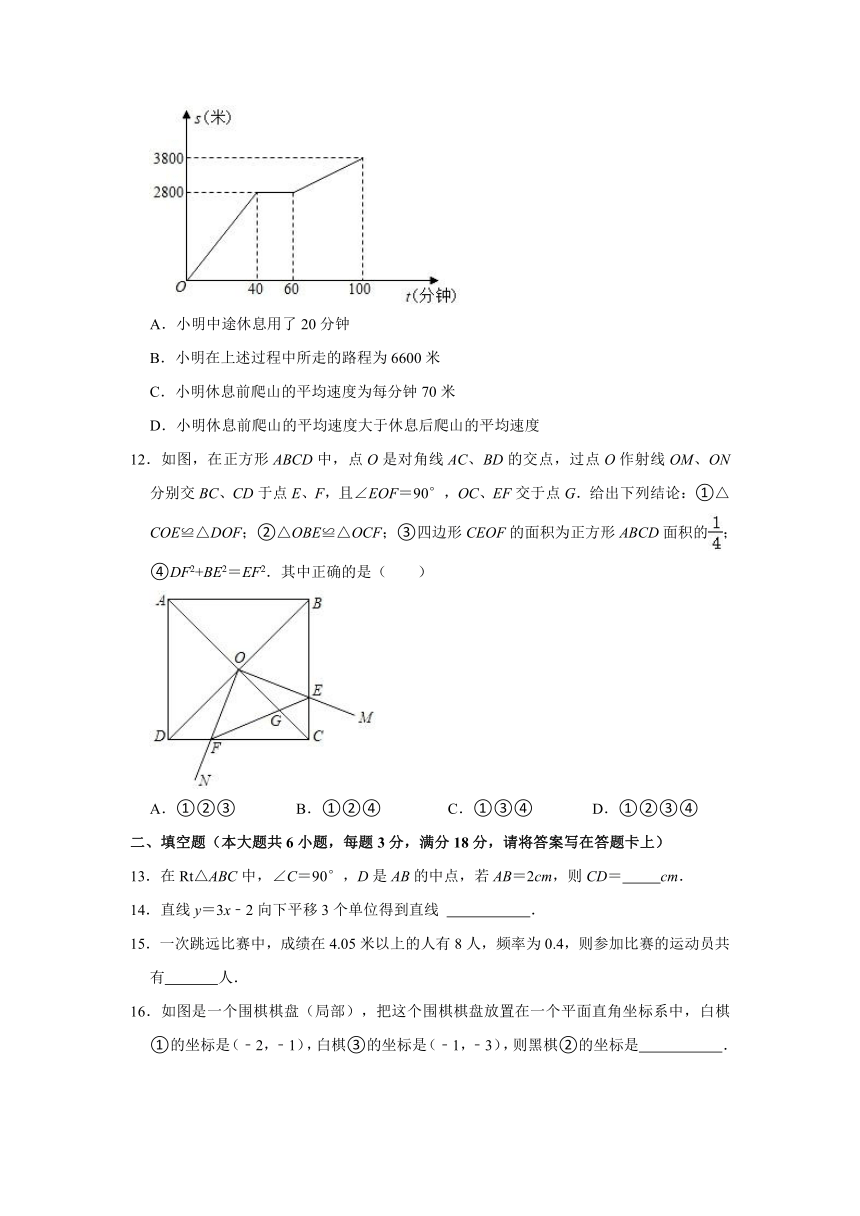
11.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间,设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
A.小明中途休息用了20分钟
B.小明在上述过程中所走的路程为6600米
C.小明休息前爬山的平均速度为每分钟70米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
12.如图,在正方形ABCD中,点O是对角线AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G.给出下列结论:①△COE≌△DOF;②△OBE≌△OCF;③四边形CEOF的面积为正方形ABCD面积的;④DF2+BE2=EF2.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题(本大题共6小题,每题3分,满分18分,请将答案写在答题卡上)
13.在Rt△ABC中,∠C=90°,D是AB的中点,若AB=2cm,则CD= cm.
14.直线y=3x﹣2向下平移3个单位得到直线 .
15.一次跳远比赛中,成绩在4.05米以上的人有8人,频率为0.4,则参加比赛的运动员共有 人.
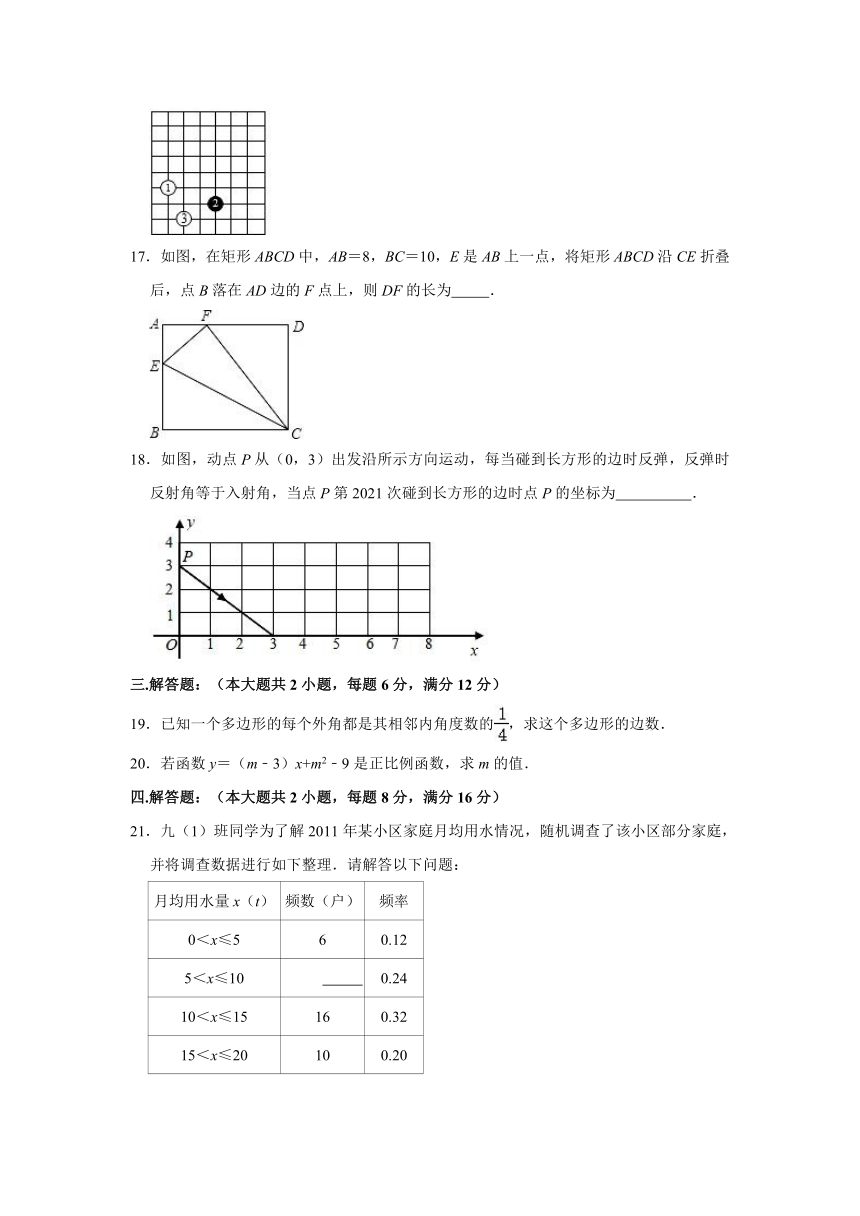
16.如图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(﹣2,﹣1),白棋③的坐标是(﹣1,﹣3),则黑棋②的坐标是 .
17.如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点上,则DF的长为 .
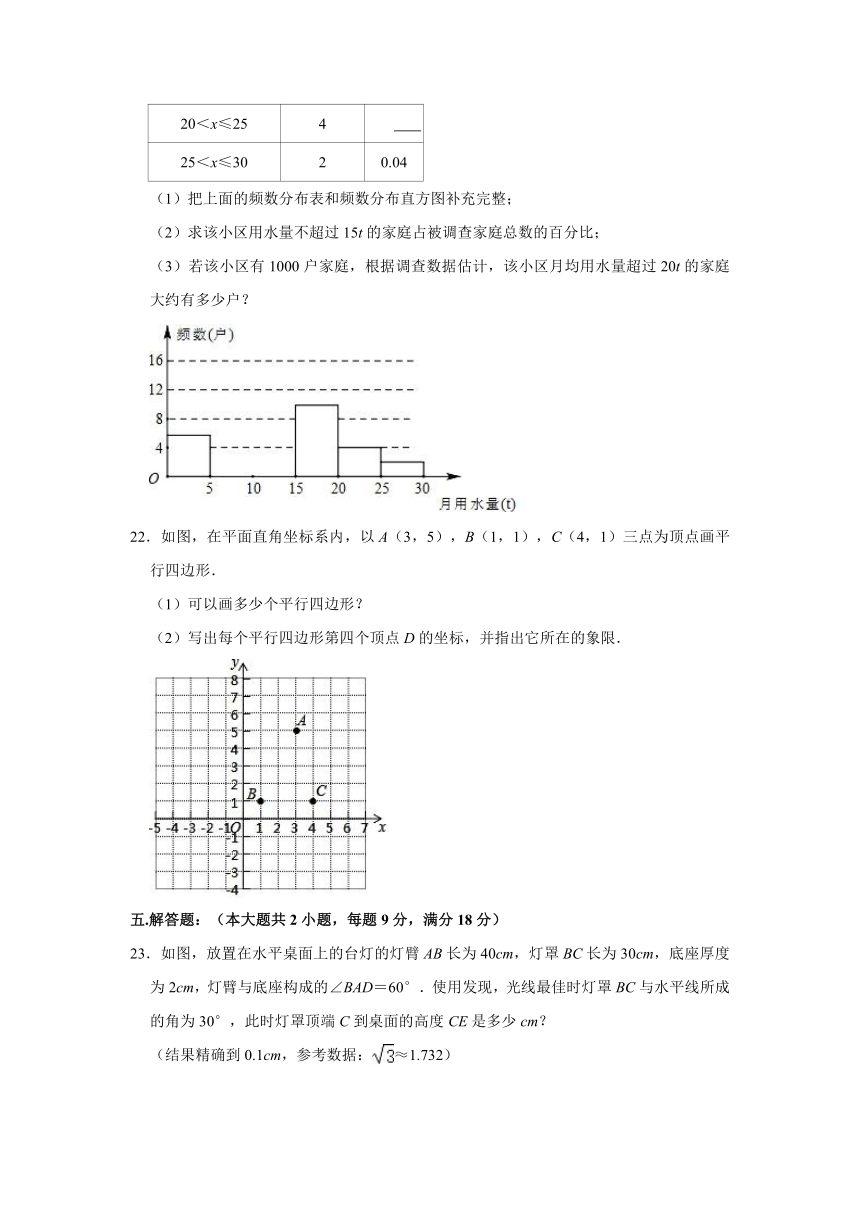
18.如图,动点P从(0,3)出发沿所示方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,当点P第2021次碰到长方形的边时点P的坐标为 .
三.解答题:(本大题共2小题,每题6分,满分12分)
19.已知一个多边形的每个外角都是其相邻内角度数的,求这个多边形的边数.
20.若函数y=(m﹣3)x+m2﹣9是正比例函数,求m的值.
四.解答题:(本大题共2小题,每题8分,满分16分)
21.九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:
月均用水量x(t) 频数(户) 频率
0<x≤5 6 0.12
5<x≤10 0.24
10<x≤15 16 0.32
15<x≤20 10 0.20
20<x≤25 4
25<x≤30 2 0.04
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
22.如图,在平面直角坐标系内,以A(3,5),B(1,1),C(4,1)三点为顶点画平行四边形.
(1)可以画多少个平行四边形?
(2)写出每个平行四边形第四个顶点D的坐标,并指出它所在的象限.
五.解答题:(本大题共2小题,每题9分,满分18分)
23.如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?
(结果精确到0.1cm,参考数据:≈1.732)
24.在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD.
六.综合与探究(本大题共2小题,每题10分,满分20分)
25.如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每秒2cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3cm的速度向C点运动,问当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
26.如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2).
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.
参考答案
一、选择题(本大题共12小题,每小题3分,满分36分,请将正确答案的序号填在答题卡上)
1.在△ABC中,已知AB=5,AC=12,BC=13,则该三角形为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形.
解:∵AB=5,AC=12,BC=13,
∴AB2+AC2=25+144=169=BC2,
∴△ABC为直角三角形.
故选:B.
2.小明3分钟共投篮80次,进了50个球,则小明进球的频率是( )
A.80 B.50 C.1.6 D.0.625
解:∵小明共投篮80次,进了50个球,
∴小明进球的频率=50÷80=0.625.
故选:D.
3.下列函数中,自变量x的取值范围是x≥3的是( )
A.y= B.y= C.y=x﹣3 D.y=
解:A、分式有意义,x﹣3≠0,解得:x≠3,故A选项错误;
B、二次根式有意义,x﹣3>0,解得x>3,故B选项错误;
C、函数式为整式,x是任意实数,故C选项错误;
D、二次根式有意义,x﹣3≥0,解得x≥3,故D选项正确.
故选:D.
4.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
【解答】A、是轴对称图形,不是中心对称图形,故本选项不符合题意;
B、不是轴对称图形,不是中心对称图形(考虑颜色),故本选项不合题意;
C、既是轴对称图形,也是中心对称图形,故本选项符合题意;
D、是轴对称图形,不是中心对称图形,故本选项不符合题意;
故选:C.
5.下列命题中,错误的是( )
A.平行四边形的对角线互相平分
B.菱形的对角线互相垂直平分
C.矩形的对角线相等且互相垂直平分
D.角平分线上的点到角两边的距离相等
解:A、平行四边形的对角线互相平分,所以A选项的说法正确;
B、菱形的对角线互相垂直平分,所以B选项的说法正确;
C、矩形的对角线相等且互相平分,所以C选项的说法错误;
D、角平分线上的点到角两边的距离相等,所以D选项的说法正确.
故选:C.
6.如图,OA是∠BAC的平分线,OM⊥AC于点M,ON⊥AB于点N,若ON=8cm,则OM长为( )
A.4cm B.5cm C.8cm D.20cm
解:∵OA是∠BAC的平分线,OM⊥AC,ON⊥AB,
∴OM=ON=8cm,
故选:C.
7.公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是( )
A.4 B.6 C.8 D.16
解:∵勾a=6,弦c=10,
∴股b==8,
∴小正方形的边长=8﹣6=2,
∴小正方形的面积=22=4
故选:A.
8.如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,若这两个多边形的内角和分别为M和N,则M+N不可能是( )
A.360° B.540° C.720° D.630°
解:一条直线将该矩形ABCD分割成两个多边形,每一个多边形的内角和都是180°的倍数,都能被180整除,分析四个答案,
只有630不能被180整除,所以M+N不可能是630°.
故选:D.
9.若点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,则m+n=( )
A.﹣2 B.0 C.3 D.5
解:∵点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,
∴m+2=4,n+5=3,
解得:m=2,n=﹣2,
故m+n=0.
故选:B.
10.正比例函数y=kx(k≠0)的图象经过第二、四象限,则一次函数y=x+k的图象大致是( )
A. B.
C. D.
解:因为正比例函数y=kx(k≠0)的图象经过第二、四象限,
所以k<0,
所以一次函数y=x+k的图象经过一、三、四象限,
故选:B.
11.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间,设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
A.小明中途休息用了20分钟
B.小明在上述过程中所走的路程为6600米
C.小明休息前爬山的平均速度为每分钟70米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
解:A、小明中途休息用了60﹣40=20分钟,正确,不符合题意;
B、小明在上述过程中所走的路程为3800米,原说法错误,符合题意;
C、小明休息前爬山的速度为=70(米/分钟),正确,不符合题意;
D、小明休息前爬山的速度为=70(米/分钟),小明休息后爬山的速度是=25(米/分钟),小明休息前爬山的平均速度大于休息后爬山的平均速度,正确,不符合题意;
故选:B.
12.如图,在正方形ABCD中,点O是对角线AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G.给出下列结论:①△COE≌△DOF;②△OBE≌△OCF;③四边形CEOF的面积为正方形ABCD面积的;④DF2+BE2=EF2.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
解:①在正方形ABCD中,OC=OD,∠COD=90°,∠ODC=∠OCB=45°,
∵∠EOF=90°,
∴∠COE=∠EOF﹣∠COF=90°﹣∠COF,
∴∠COE=∠DOF,
∴△COE≌△DOF(ASA),
故①正确;
②在正方形ABCD中,OC=OB,∠COB=90°,∠OBC=∠OCB=45°,
∵∠EOF=90°,
∴∠BOE=∠COF,
∴△OBE≌△OCF(ASA);故②正确;
③由①全等可得四边形CEOF的面积与△OCD面积相等,
∴四边形CEOF的面积为正方形ABCD面积的,
故③正确;
④∵△COE≌△DOF,
∴CE=DF,
∵四边形ABCD为正方形,
∴BC=CD,
∴BE=CF,
在Rt△ECF中,CE2+CF2=EF2,
∴DF2+BE2=EF2,
故④正确;
综上所述,正确的是①②③④,
故选:D.
二、填空题(本大题共6小题,每题3分,满分18分,请将答案写在答题卡上)
13.在Rt△ABC中,∠C=90°,D是AB的中点,若AB=2cm,则CD= 1 cm.
解:在Rt△ABC中,∠C=90°,
∵D是AB的中点,
∴CD=AB,
∵AB=2cm,
∴CD=1cm,
故答案为:1.
14.直线y=3x﹣2向下平移3个单位得到直线 y=3x﹣5 .
解:直线y=3x﹣2向下平移3个单位长度后得到的直线解析式为y=3x﹣2﹣3,即y=3x﹣5.
故答案为y=3x﹣5.
15.一次跳远比赛中,成绩在4.05米以上的人有8人,频率为0.4,则参加比赛的运动员共有 20 人.
解:∵成绩在4.05米以上的频数是8,频率是0.4,
∴参加比赛的运动员=8÷0.4=20.
故答案为:20.
16.如图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(﹣2,﹣1),白棋③的坐标是(﹣1,﹣3),则黑棋②的坐标是 (1,﹣2) .
解:由用(﹣2,﹣1)表示白棋①的位置,用(﹣1,﹣3)表示白棋③的位置知,y轴为从左向数的第四条竖直直线,且向上为正方向,x轴是从下往上数第五条水平直线,这两条直线交点为坐标原点.那么黑棋②的位置为(1,﹣2).
故答案为:(1,﹣2).
17.如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点上,则DF的长为 6 .
解:∵四边形ABCD是矩形,
∴AB=DC=8,∠D=90°,
∵将矩形ABCD沿CE折叠后,点B落在AD边的F点上,
∴CF=BC=10,
在Rt△CDF中,由勾股定理得:DF===6,
故答案为:6.
18.如图,动点P从(0,3)出发沿所示方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,当点P第2021次碰到长方形的边时点P的坐标为 (1,4) .
解:如图所示:经过6次反弹后动点回到出发点(0,3),
∵2021÷6=336…5,
∴当点P第2021次碰到矩形的边时为第337个循环组的第5次反弹,
∴点P的坐标为(1,4).
故答案为:(1,4).
三.解答题:(本大题共2小题,每题6分,满分12分)
19.已知一个多边形的每个外角都是其相邻内角度数的,求这个多边形的边数.
解:设这个多边形的一个外角的度数为x,则
x=(180°﹣x),
解得:x=36°,
360÷36=10,
答:这个多边形的边数为10.
20.若函数y=(m﹣3)x+m2﹣9是正比例函数,求m的值.
解:∵y=(m﹣3)x+m2﹣9是正比例函数,
∴m2﹣9=0,m﹣3≠0,
解得m=﹣3.
四.解答题:(本大题共2小题,每题8分,满分16分)
21.九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:
月均用水量x(t) 频数(户) 频率
0<x≤5 6 0.12
5<x≤10 12 0.24
10<x≤15 16 0.32
15<x≤20 10 0.20
20<x≤25 4 0.08
25<x≤30 2 0.04
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
解:(1)如图所示:根据0<x≤5中频数为6,频率为0.12,
则6÷0.12=50,50×0.24=12户,4÷50=0.08,
故表格从上往下依次是:12和0.08;
(2)×100%=68%;
(3)1000×(0.08+0.04)=120户,
答:该小区月均用水量超过20t的家庭大约有120户.
22.如图,在平面直角坐标系内,以A(3,5),B(1,1),C(4,1)三点为顶点画平行四边形.
(1)可以画多少个平行四边形?
(2)写出每个平行四边形第四个顶点D的坐标,并指出它所在的象限.
解:(1)可以画3个平行四边形;如图所示:
(2)由A(3,5),B(1,1),C(4,1),得BC=3,
则点D的位置可由点A向左平移3个单位,
∴D(0,5),在y轴上;
同理:点D的位置可由点A向右平移3个单位,
∴D(6,5),在第一象限;
以AC为边,则点D的位置B向下平移4个单位、再向右平移1个单位,
∴D(2,﹣3),在第四象限.
五.解答题:(本大题共2小题,每题9分,满分18分)
23.如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?
(结果精确到0.1cm,参考数据:≈1.732)
解:由题意得:AD⊥CE,过点B作BM⊥CE,BF⊥EA,
∵灯罩BC长为30cm,光线最佳时灯罩BC与水平线所成的角为30°,
∵CM⊥MB,即三角形CMB为直角三角形,
∴sin30°==,
∴CM=15cm,
在直角三角形ABF中,sin60°=,
∴=,
解得:BF=20,
又∠ADC=∠BMD=∠BFD=90°,
∴四边形BFDM为矩形,
∴MD=BF,
∴CE=CM+MD+DE=CM+BF+ED=15+20+2≈51.6cm.
答:此时灯罩顶端C到桌面的高度CE是51.6cm.
24.在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD.
【解答】证明:(1)在矩形ABCD中,∵AD∥BC,
∴∠AEB=∠DAF,
又∵DF⊥AE,
∴∠DFA=90°,
∴∠DFA=∠B,
又∵AD=EA,
∴△ADF≌△EAB,
∴DF=AB.
(2)∵∠ADF+∠FDC=90°,∠DAF+∠ADF=90°,
∴∠FDC=∠DAF=30°,
∴AD=2DF,
∵DF=AB,
∴AD=2AB=8.
六.综合与探究(本大题共2小题,每题10分,满分20分)
25.如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每秒2cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3cm的速度向C点运动,问当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
【解答】(1)证明:∵AB=AC,AD⊥BC,
∴D为BC的中点,
∵E,F分别为AB,AC的中点,
∴DE和DF是△ABC的中位线,
∴DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∵E,F分别为AB,AC的中点,AB=AC,
∴AE=AF∴平行四边形AEDF是菱形;
(2)解:∵EF为△ABC的中位线,
∴EF=BC=5,
∵AD=8,AD⊥EF,
∴S菱形AEDF=AD?EF=×8×5=20;
(3)解:∵EF∥BC
∴EH∥BP,
若四边形BPHE为平行四边形,则需EH=BP,
∴5﹣2t=3t,解得:t=1,
∴当t=1秒时,四边形BPHE为平行四边形,
∵EF∥BC,
∴FH∥PC,
若四边形PCFH为平行四边形,则需FH=PC,
∴2t=10﹣3t,解得:t=2,
∴当t=2秒时,四边形PCFH为平行四边形.
26.如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2).
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.
解:(1)设直线AB的解析式是y=kx+b,
根据题意得:,
解得:,
则直线的解析式是:y=﹣x+6;
(2)在y=﹣x+6中,令x=0,解得:y=6,
S△OAC=×6×4=12;
(3)①若∠BAM=90°,过点A作AM1⊥AB交y轴于M1,过点A作AD⊥y轴于D,则D(0,2).
∵OC=OB=6,∠BOC=90°,
∴△BOC是等腰直角三角形,
∴∠BCO=45°,
∴△CAM1也是等腰直角三角形,
∴DM1=CD=6﹣2=4,
∴OM1=2,
∴M1(0,﹣2)
②若∠ABM=90°,过点B作BM2⊥AB交y轴与M2,同样求得M2(0,﹣6),
综上所述,满足条件的点M的坐标为(0,﹣2)或(0,﹣6)
一、选择题(本大题共12小题,每小题3分,满分36分,请将正确答案的序号填在答题卡上)
1.在△ABC中,已知AB=5,AC=12,BC=13,则该三角形为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形.
2.小明3分钟共投篮80次,进了50个球,则小明进球的频率是( )
A.80 B.50 C.1.6 D.0.625
3.下列函数中,自变量x的取值范围是x≥3的是( )
A.y= B.y= C.y=x﹣3 D.y=
4.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
5.下列命题中,错误的是( )
A.平行四边形的对角线互相平分
B.菱形的对角线互相垂直平分
C.矩形的对角线相等且互相垂直平分
D.角平分线上的点到角两边的距离相等
6.如图,OA是∠BAC的平分线,OM⊥AC于点M,ON⊥AB于点N,若ON=8cm,则OM长为( )
A.4cm B.5cm C.8cm D.20cm
7.公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是( )
A.4 B.6 C.8 D.16
8.如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,若这两个多边形的内角和分别为M和N,则M+N不可能是( )
A.360° B.540° C.720° D.630°
9.若点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,则m+n=( )
A.﹣2 B.0 C.3 D.5
10.正比例函数y=kx(k≠0)的图象经过第二、四象限,则一次函数y=x+k的图象大致是( )
A. B.
C. D.
11.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间,设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
A.小明中途休息用了20分钟
B.小明在上述过程中所走的路程为6600米
C.小明休息前爬山的平均速度为每分钟70米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
12.如图,在正方形ABCD中,点O是对角线AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G.给出下列结论:①△COE≌△DOF;②△OBE≌△OCF;③四边形CEOF的面积为正方形ABCD面积的;④DF2+BE2=EF2.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题(本大题共6小题,每题3分,满分18分,请将答案写在答题卡上)
13.在Rt△ABC中,∠C=90°,D是AB的中点,若AB=2cm,则CD= cm.
14.直线y=3x﹣2向下平移3个单位得到直线 .
15.一次跳远比赛中,成绩在4.05米以上的人有8人,频率为0.4,则参加比赛的运动员共有 人.
16.如图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(﹣2,﹣1),白棋③的坐标是(﹣1,﹣3),则黑棋②的坐标是 .
17.如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点上,则DF的长为 .
18.如图,动点P从(0,3)出发沿所示方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,当点P第2021次碰到长方形的边时点P的坐标为 .
三.解答题:(本大题共2小题,每题6分,满分12分)
19.已知一个多边形的每个外角都是其相邻内角度数的,求这个多边形的边数.
20.若函数y=(m﹣3)x+m2﹣9是正比例函数,求m的值.
四.解答题:(本大题共2小题,每题8分,满分16分)
21.九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:
月均用水量x(t) 频数(户) 频率
0<x≤5 6 0.12
5<x≤10 0.24
10<x≤15 16 0.32
15<x≤20 10 0.20
20<x≤25 4
25<x≤30 2 0.04
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
22.如图,在平面直角坐标系内,以A(3,5),B(1,1),C(4,1)三点为顶点画平行四边形.
(1)可以画多少个平行四边形?
(2)写出每个平行四边形第四个顶点D的坐标,并指出它所在的象限.
五.解答题:(本大题共2小题,每题9分,满分18分)
23.如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?
(结果精确到0.1cm,参考数据:≈1.732)
24.在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD.
六.综合与探究(本大题共2小题,每题10分,满分20分)
25.如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每秒2cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3cm的速度向C点运动,问当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
26.如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2).
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.
参考答案
一、选择题(本大题共12小题,每小题3分,满分36分,请将正确答案的序号填在答题卡上)
1.在△ABC中,已知AB=5,AC=12,BC=13,则该三角形为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形.
解:∵AB=5,AC=12,BC=13,
∴AB2+AC2=25+144=169=BC2,
∴△ABC为直角三角形.
故选:B.
2.小明3分钟共投篮80次,进了50个球,则小明进球的频率是( )
A.80 B.50 C.1.6 D.0.625
解:∵小明共投篮80次,进了50个球,
∴小明进球的频率=50÷80=0.625.
故选:D.
3.下列函数中,自变量x的取值范围是x≥3的是( )
A.y= B.y= C.y=x﹣3 D.y=
解:A、分式有意义,x﹣3≠0,解得:x≠3,故A选项错误;
B、二次根式有意义,x﹣3>0,解得x>3,故B选项错误;
C、函数式为整式,x是任意实数,故C选项错误;
D、二次根式有意义,x﹣3≥0,解得x≥3,故D选项正确.
故选:D.
4.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
【解答】A、是轴对称图形,不是中心对称图形,故本选项不符合题意;
B、不是轴对称图形,不是中心对称图形(考虑颜色),故本选项不合题意;
C、既是轴对称图形,也是中心对称图形,故本选项符合题意;
D、是轴对称图形,不是中心对称图形,故本选项不符合题意;
故选:C.
5.下列命题中,错误的是( )
A.平行四边形的对角线互相平分
B.菱形的对角线互相垂直平分
C.矩形的对角线相等且互相垂直平分
D.角平分线上的点到角两边的距离相等
解:A、平行四边形的对角线互相平分,所以A选项的说法正确;
B、菱形的对角线互相垂直平分,所以B选项的说法正确;
C、矩形的对角线相等且互相平分,所以C选项的说法错误;
D、角平分线上的点到角两边的距离相等,所以D选项的说法正确.
故选:C.
6.如图,OA是∠BAC的平分线,OM⊥AC于点M,ON⊥AB于点N,若ON=8cm,则OM长为( )
A.4cm B.5cm C.8cm D.20cm
解:∵OA是∠BAC的平分线,OM⊥AC,ON⊥AB,
∴OM=ON=8cm,
故选:C.
7.公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是( )
A.4 B.6 C.8 D.16
解:∵勾a=6,弦c=10,
∴股b==8,
∴小正方形的边长=8﹣6=2,
∴小正方形的面积=22=4
故选:A.
8.如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,若这两个多边形的内角和分别为M和N,则M+N不可能是( )
A.360° B.540° C.720° D.630°
解:一条直线将该矩形ABCD分割成两个多边形,每一个多边形的内角和都是180°的倍数,都能被180整除,分析四个答案,
只有630不能被180整除,所以M+N不可能是630°.
故选:D.
9.若点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,则m+n=( )
A.﹣2 B.0 C.3 D.5
解:∵点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,
∴m+2=4,n+5=3,
解得:m=2,n=﹣2,
故m+n=0.
故选:B.
10.正比例函数y=kx(k≠0)的图象经过第二、四象限,则一次函数y=x+k的图象大致是( )
A. B.
C. D.
解:因为正比例函数y=kx(k≠0)的图象经过第二、四象限,
所以k<0,
所以一次函数y=x+k的图象经过一、三、四象限,
故选:B.
11.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间,设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
A.小明中途休息用了20分钟
B.小明在上述过程中所走的路程为6600米
C.小明休息前爬山的平均速度为每分钟70米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
解:A、小明中途休息用了60﹣40=20分钟,正确,不符合题意;
B、小明在上述过程中所走的路程为3800米,原说法错误,符合题意;
C、小明休息前爬山的速度为=70(米/分钟),正确,不符合题意;
D、小明休息前爬山的速度为=70(米/分钟),小明休息后爬山的速度是=25(米/分钟),小明休息前爬山的平均速度大于休息后爬山的平均速度,正确,不符合题意;
故选:B.
12.如图,在正方形ABCD中,点O是对角线AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G.给出下列结论:①△COE≌△DOF;②△OBE≌△OCF;③四边形CEOF的面积为正方形ABCD面积的;④DF2+BE2=EF2.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
解:①在正方形ABCD中,OC=OD,∠COD=90°,∠ODC=∠OCB=45°,
∵∠EOF=90°,
∴∠COE=∠EOF﹣∠COF=90°﹣∠COF,
∴∠COE=∠DOF,
∴△COE≌△DOF(ASA),
故①正确;
②在正方形ABCD中,OC=OB,∠COB=90°,∠OBC=∠OCB=45°,
∵∠EOF=90°,
∴∠BOE=∠COF,
∴△OBE≌△OCF(ASA);故②正确;
③由①全等可得四边形CEOF的面积与△OCD面积相等,
∴四边形CEOF的面积为正方形ABCD面积的,
故③正确;
④∵△COE≌△DOF,
∴CE=DF,
∵四边形ABCD为正方形,
∴BC=CD,
∴BE=CF,
在Rt△ECF中,CE2+CF2=EF2,
∴DF2+BE2=EF2,
故④正确;
综上所述,正确的是①②③④,
故选:D.
二、填空题(本大题共6小题,每题3分,满分18分,请将答案写在答题卡上)
13.在Rt△ABC中,∠C=90°,D是AB的中点,若AB=2cm,则CD= 1 cm.
解:在Rt△ABC中,∠C=90°,
∵D是AB的中点,
∴CD=AB,
∵AB=2cm,
∴CD=1cm,
故答案为:1.
14.直线y=3x﹣2向下平移3个单位得到直线 y=3x﹣5 .
解:直线y=3x﹣2向下平移3个单位长度后得到的直线解析式为y=3x﹣2﹣3,即y=3x﹣5.
故答案为y=3x﹣5.
15.一次跳远比赛中,成绩在4.05米以上的人有8人,频率为0.4,则参加比赛的运动员共有 20 人.
解:∵成绩在4.05米以上的频数是8,频率是0.4,
∴参加比赛的运动员=8÷0.4=20.
故答案为:20.
16.如图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(﹣2,﹣1),白棋③的坐标是(﹣1,﹣3),则黑棋②的坐标是 (1,﹣2) .
解:由用(﹣2,﹣1)表示白棋①的位置,用(﹣1,﹣3)表示白棋③的位置知,y轴为从左向数的第四条竖直直线,且向上为正方向,x轴是从下往上数第五条水平直线,这两条直线交点为坐标原点.那么黑棋②的位置为(1,﹣2).
故答案为:(1,﹣2).
17.如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点上,则DF的长为 6 .
解:∵四边形ABCD是矩形,
∴AB=DC=8,∠D=90°,
∵将矩形ABCD沿CE折叠后,点B落在AD边的F点上,
∴CF=BC=10,
在Rt△CDF中,由勾股定理得:DF===6,
故答案为:6.
18.如图,动点P从(0,3)出发沿所示方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,当点P第2021次碰到长方形的边时点P的坐标为 (1,4) .
解:如图所示:经过6次反弹后动点回到出发点(0,3),
∵2021÷6=336…5,
∴当点P第2021次碰到矩形的边时为第337个循环组的第5次反弹,
∴点P的坐标为(1,4).
故答案为:(1,4).
三.解答题:(本大题共2小题,每题6分,满分12分)
19.已知一个多边形的每个外角都是其相邻内角度数的,求这个多边形的边数.
解:设这个多边形的一个外角的度数为x,则
x=(180°﹣x),
解得:x=36°,
360÷36=10,
答:这个多边形的边数为10.
20.若函数y=(m﹣3)x+m2﹣9是正比例函数,求m的值.
解:∵y=(m﹣3)x+m2﹣9是正比例函数,
∴m2﹣9=0,m﹣3≠0,
解得m=﹣3.
四.解答题:(本大题共2小题,每题8分,满分16分)
21.九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:
月均用水量x(t) 频数(户) 频率
0<x≤5 6 0.12
5<x≤10 12 0.24
10<x≤15 16 0.32
15<x≤20 10 0.20
20<x≤25 4 0.08
25<x≤30 2 0.04
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
解:(1)如图所示:根据0<x≤5中频数为6,频率为0.12,
则6÷0.12=50,50×0.24=12户,4÷50=0.08,
故表格从上往下依次是:12和0.08;
(2)×100%=68%;
(3)1000×(0.08+0.04)=120户,
答:该小区月均用水量超过20t的家庭大约有120户.
22.如图,在平面直角坐标系内,以A(3,5),B(1,1),C(4,1)三点为顶点画平行四边形.
(1)可以画多少个平行四边形?
(2)写出每个平行四边形第四个顶点D的坐标,并指出它所在的象限.
解:(1)可以画3个平行四边形;如图所示:
(2)由A(3,5),B(1,1),C(4,1),得BC=3,
则点D的位置可由点A向左平移3个单位,
∴D(0,5),在y轴上;
同理:点D的位置可由点A向右平移3个单位,
∴D(6,5),在第一象限;
以AC为边,则点D的位置B向下平移4个单位、再向右平移1个单位,
∴D(2,﹣3),在第四象限.
五.解答题:(本大题共2小题,每题9分,满分18分)
23.如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?
(结果精确到0.1cm,参考数据:≈1.732)
解:由题意得:AD⊥CE,过点B作BM⊥CE,BF⊥EA,
∵灯罩BC长为30cm,光线最佳时灯罩BC与水平线所成的角为30°,
∵CM⊥MB,即三角形CMB为直角三角形,
∴sin30°==,
∴CM=15cm,
在直角三角形ABF中,sin60°=,
∴=,
解得:BF=20,
又∠ADC=∠BMD=∠BFD=90°,
∴四边形BFDM为矩形,
∴MD=BF,
∴CE=CM+MD+DE=CM+BF+ED=15+20+2≈51.6cm.
答:此时灯罩顶端C到桌面的高度CE是51.6cm.
24.在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD.
【解答】证明:(1)在矩形ABCD中,∵AD∥BC,
∴∠AEB=∠DAF,
又∵DF⊥AE,
∴∠DFA=90°,
∴∠DFA=∠B,
又∵AD=EA,
∴△ADF≌△EAB,
∴DF=AB.
(2)∵∠ADF+∠FDC=90°,∠DAF+∠ADF=90°,
∴∠FDC=∠DAF=30°,
∴AD=2DF,
∵DF=AB,
∴AD=2AB=8.
六.综合与探究(本大题共2小题,每题10分,满分20分)
25.如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每秒2cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3cm的速度向C点运动,问当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
【解答】(1)证明:∵AB=AC,AD⊥BC,
∴D为BC的中点,
∵E,F分别为AB,AC的中点,
∴DE和DF是△ABC的中位线,
∴DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∵E,F分别为AB,AC的中点,AB=AC,
∴AE=AF∴平行四边形AEDF是菱形;
(2)解:∵EF为△ABC的中位线,
∴EF=BC=5,
∵AD=8,AD⊥EF,
∴S菱形AEDF=AD?EF=×8×5=20;
(3)解:∵EF∥BC
∴EH∥BP,
若四边形BPHE为平行四边形,则需EH=BP,
∴5﹣2t=3t,解得:t=1,
∴当t=1秒时,四边形BPHE为平行四边形,
∵EF∥BC,
∴FH∥PC,
若四边形PCFH为平行四边形,则需FH=PC,
∴2t=10﹣3t,解得:t=2,
∴当t=2秒时,四边形PCFH为平行四边形.
26.如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2).
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.
解:(1)设直线AB的解析式是y=kx+b,
根据题意得:,
解得:,
则直线的解析式是:y=﹣x+6;
(2)在y=﹣x+6中,令x=0,解得:y=6,
S△OAC=×6×4=12;
(3)①若∠BAM=90°,过点A作AM1⊥AB交y轴于M1,过点A作AD⊥y轴于D,则D(0,2).
∵OC=OB=6,∠BOC=90°,
∴△BOC是等腰直角三角形,
∴∠BCO=45°,
∴△CAM1也是等腰直角三角形,
∴DM1=CD=6﹣2=4,
∴OM1=2,
∴M1(0,﹣2)
②若∠ABM=90°,过点B作BM2⊥AB交y轴与M2,同样求得M2(0,﹣6),
综上所述,满足条件的点M的坐标为(0,﹣2)或(0,﹣6)
同课章节目录
