2020-2021学年湖南省岳阳市岳阳县八年级(下)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年湖南省岳阳市岳阳县八年级(下)期末数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 811.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-02 08:31:37 | ||
图片预览

文档简介
2020-2021学年湖南省岳阳市岳阳县八年级(下)期末数学试卷
一、选择题(每小题3分,共30分)
1.下列既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.直线y=x﹣1的图象经过( )
A.第二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第一、二、三象限
3.在平面直角坐标系中,点P(﹣1,﹣2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.五边形的内角和为( )
A.360° B.540° C.720° D.900°
5.菱形具有而平行四边形不一定具有的性质是( )
A.两组对边分别平行 B.两组对角分别相等
C.对角线互相平分 D.对角线互相垂直
6.顺次连接矩形四边中点所得的四边形一定是( )
A.正方形 B.矩形 C.菱形 D.等腰梯形
7.一个三角形的周长是36cm,则以这个三角形各边中点为顶点的三角形的周长是( )
A.6cm B.12cm C.18cm D.36cm
8.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B.5 C.4 D.7
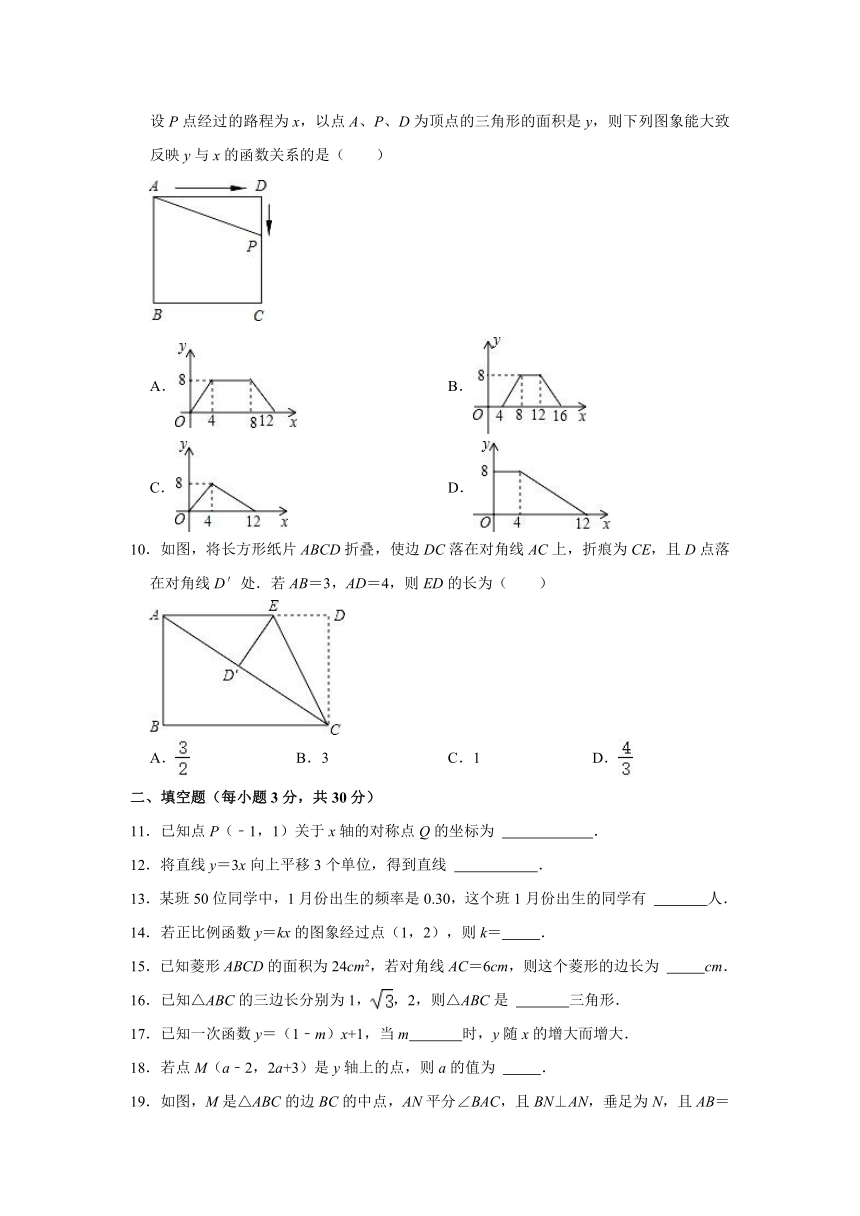
9.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是( )
A. B.
C. D.
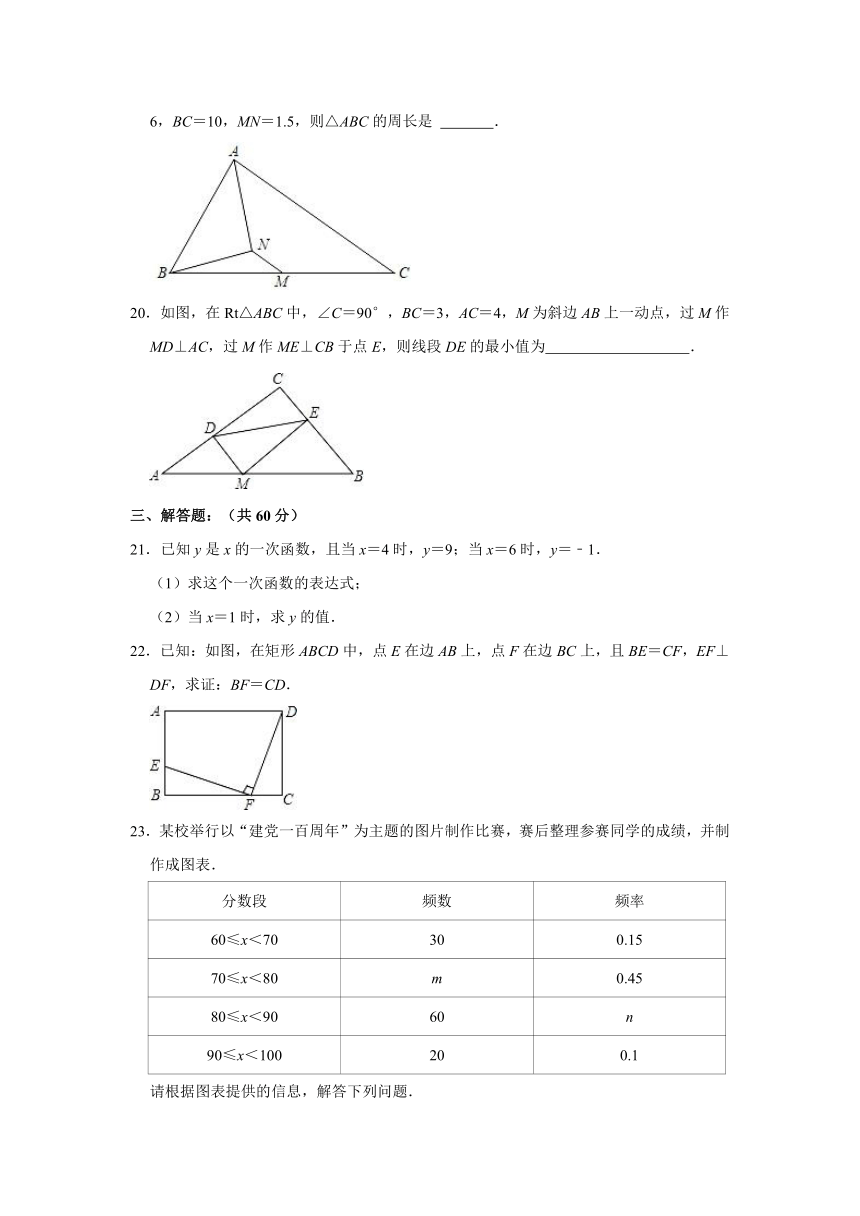
10.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( )
A. B.3 C.1 D.
二、填空题(每小题3分,共30分)
11.已知点P(﹣1,1)关于x轴的对称点Q的坐标为 .
12.将直线y=3x向上平移3个单位,得到直线 .
13.某班50位同学中,1月份出生的频率是0.30,这个班1月份出生的同学有 人.
14.若正比例函数y=kx的图象经过点(1,2),则k= .
15.已知菱形ABCD的面积为24cm2,若对角线AC=6cm,则这个菱形的边长为 cm.
16.已知△ABC的三边长分别为1,,2,则△ABC是 三角形.
17.已知一次函数y=(1﹣m)x+1,当m 时,y随x的增大而增大.
18.若点M(a﹣2,2a+3)是y轴上的点,则a的值为 .
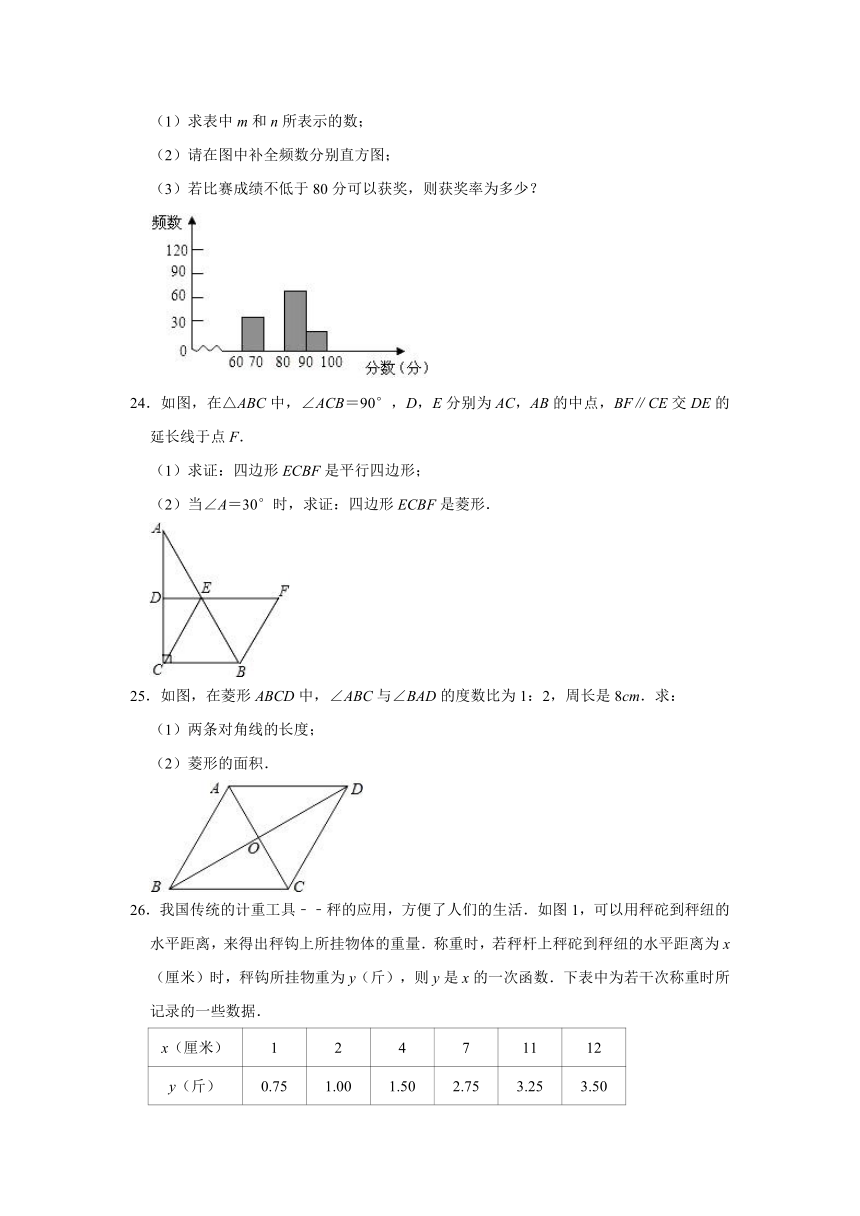
19.如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,则△ABC的周长是 .
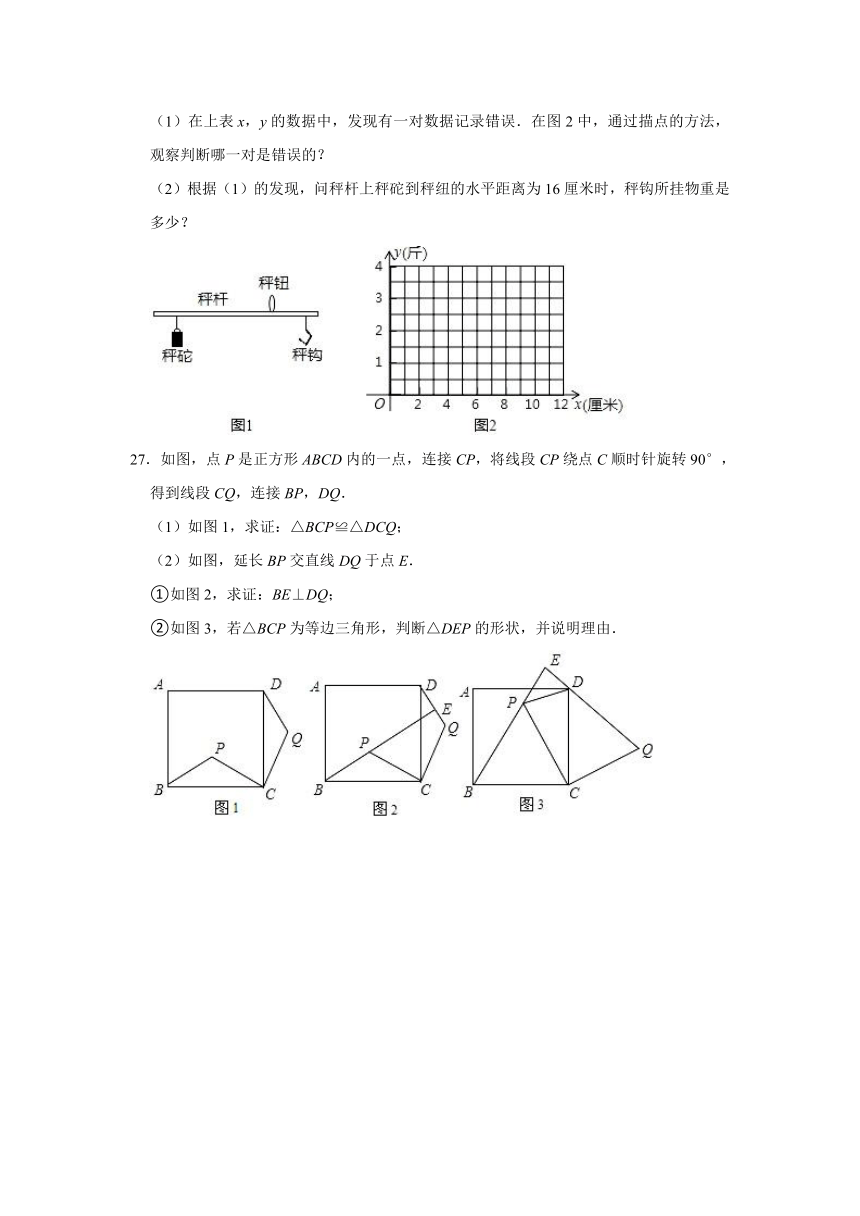
20.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为 .
三、解答题:(共60分)
21.已知y是x的一次函数,且当x=4时,y=9;当x=6时,y=﹣1.
(1)求这个一次函数的表达式;
(2)当x=1时,求y的值.
22.已知:如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
23.某校举行以“建党一百周年”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表.
分数段 频数 频率
60≤x<70 30 0.15
70≤x<80 m 0.45
80≤x<90 60 n
90≤x<100 20 0.1
请根据图表提供的信息,解答下列问题.
(1)求表中m和n所表示的数;
(2)请在图中补全频数分别直方图;
(3)若比赛成绩不低于80分可以获奖,则获奖率为多少?
24.如图,在△ABC中,∠ACB=90°,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
(1)求证:四边形ECBF是平行四边形;
(2)当∠A=30°时,求证:四边形ECBF是菱形.
25.如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm.求:
(1)两条对角线的长度;
(2)菱形的面积.
26.我国传统的计重工具﹣﹣秤的应用,方便了人们的生活.如图1,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量.称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数.下表中为若干次称重时所记录的一些数据.
x(厘米) 1 2 4 7 11 12
y(斤) 0.75 1.00 1.50 2.75 3.25 3.50
(1)在上表x,y的数据中,发现有一对数据记录错误.在图2中,通过描点的方法,观察判断哪一对是错误的?
(2)根据(1)的发现,问秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少?
27.如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
(1)如图1,求证:△BCP≌△DCQ;
(2)如图,延长BP交直线DQ于点E.
①如图2,求证:BE⊥DQ;
②如图3,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
参考答案
一、选择题(每小题3分,共30分)
1.下列既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
解:A、是轴对称图形,也是中心对称图形;
B、是轴对称图形,不是中心对称图形;
C、是轴对称图形,不是中心对称图形;
D、不是轴对称图形,也不是中心对称图形.
故选:A.
2.直线y=x﹣1的图象经过( )
A.第二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第一、二、三象限
解:直线y=x﹣1与y轴交于(0,﹣1)点,
且k=1>0,y随x的增大而增大,
∴直线y=x﹣1的图象经过第一、三、四象限.
故选:C.
3.在平面直角坐标系中,点P(﹣1,﹣2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:点P(﹣1,﹣2),由横纵坐标均为负数,则此点在第三象限.
故选:C.
4.五边形的内角和为( )
A.360° B.540° C.720° D.900°
解:五边形的内角和是(5﹣2)×180°=540°.故选:B.
5.菱形具有而平行四边形不一定具有的性质是( )
A.两组对边分别平行 B.两组对角分别相等
C.对角线互相平分 D.对角线互相垂直
解:A、不正确,两组对边分别平行;
B、不正确,两组对角分别相等,两者均有此性质正确,;
C、不正确,对角线互相平分,两者均具有此性质;
D、菱形的对角线互相垂直但平行四边形却无此性质.
故选:D.
6.顺次连接矩形四边中点所得的四边形一定是( )
A.正方形 B.矩形 C.菱形 D.等腰梯形
解:连接AC、BD,
在△ABD中,
∵AH=HD,AE=EB
∴EH=BD,
同理FG=BD,HG=AC,EF=AC,
又∵在矩形ABCD中,AC=BD,
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.
故选:C.
7.一个三角形的周长是36cm,则以这个三角形各边中点为顶点的三角形的周长是( )
A.6cm B.12cm C.18cm D.36cm
解:如图,点D、E、F分别是AB、AC、BC的中点,
∴DE=BC,DF=AC,EF=AB,
∵原三角形的周长为36cm,
则新三角形的周长为=18(cm).
故选:C.
8.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B.5 C.4 D.7
解:作EF⊥BC于F,
∵BE平分∠ABC,EF⊥BC,ED⊥AB,
∴EF=DE=2,
∴△BCE的面积=×BC×EF=5.
故选:B.
9.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是( )
A. B.
C. D.
解:当点P由点A向点D运动,即0<x≤4时,y的值为0;
当点P在DC上运动,即4<x≤8时,y随着x的增大而增大;
当点P在CB上运动,即8<x≤12时,y不变;
当点P在BA上运动,即12<x≤16时,y随x的增大而减小.
故选:B.
10.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( )
A. B.3 C.1 D.
解:∵AB=3,AD=4,
∴DC=3,
∴AC==5,
根据折叠可得:△DEC≌△D′EC,
∴D′C=DC=3,DE=D′E,
设ED=x,则D′E=x,AD′=AC﹣CD′=2,AE=4﹣x,
在Rt△AED′中:(AD′)2+(ED′)2=AE2,
22+x2=(4﹣x)2,
解得:x=,
故选:A.
二、填空题(每小题3分,共30分)
11.已知点P(﹣1,1)关于x轴的对称点Q的坐标为 (﹣1,﹣1) .
解:点P(﹣1,1)关于x轴的对称点Q的坐标为:(﹣1,﹣1).
故答案为:(﹣1,﹣1).
12.将直线y=3x向上平移3个单位,得到直线 y=3x+3 .
解:将直线y=3x向上平移3个单位,得到直线:y=3x+3.
故答案为y=3x+3.
13.某班50位同学中,1月份出生的频率是0.30,这个班1月份出生的同学有 15 人.
解:50×0.30=15(人),
故答案为:15.
14.若正比例函数y=kx的图象经过点(1,2),则k= 2 .
解:∵正比例函数y=kx的图象经过点(1,2),
∴2=k×1,即k=2.
故答案为:2.
15.已知菱形ABCD的面积为24cm2,若对角线AC=6cm,则这个菱形的边长为 5 cm.
解:菱形ABCD的面积=AC?BD,
∵菱形ABCD的面积是24cm2,其中一条对角线AC长6cm,
∴另一条对角线BD的长=8cm;
边长是:=5cm.
故答案为:5.
16.已知△ABC的三边长分别为1,,2,则△ABC是 直角 三角形.
解:∵12+()2=22,
∴△ABC是直角三角形.
故答案为:直角.
17.已知一次函数y=(1﹣m)x+1,当m <1 时,y随x的增大而增大.
解:当1﹣m>0时,y随x的增大而增大,
所以m<1.
故答案为:<1.
18.若点M(a﹣2,2a+3)是y轴上的点,则a的值为 2 .
解:∵点M(a﹣2,2a+3)是y轴上的点,
∴a﹣2=0,
解得a=2.
故答案为:2.
19.如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,则△ABC的周长是 25 .
解:延长线段BN交AC于E.
∵AN平分∠BAC,
∴∠BAN=∠EAN,
∵BN⊥AN,
∴∠ANB=∠ANE=90°,
在△ABN和△AEN中,
,
∴△ABN≌△AEN(ASA),
∴AE=AB=6,BN=NE,
又∵M是△ABC的边BC的中点,
∴CE=2MN=2×1.5=3,
∴△ABC的周长是AB+BC+AC=6+10+6+3=25,
故答案为:25.
20.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为 .
解:连接CM,如图所示:
∵MD⊥AC,ME⊥CB,
∴∠MDC=∠MEC=90°,
∵∠C=90°,
∴四边形CDME是矩形,
∴DE=CM,
∵∠C=90°,BC=3,AC=4,
∴AB===5,
当CM⊥AB时,CM最短,此时△ABC的面积=AB?CM=BC?AC,
∴CM的最小值==,
∴线段DE的最小值为;
故答案为:.
三、解答题:(共60分)
21.已知y是x的一次函数,且当x=4时,y=9;当x=6时,y=﹣1.
(1)求这个一次函数的表达式;
(2)当x=1时,求y的值.
解:(1)设这个一次函数的解析式为y=kx+b(k≠0),
∵当x=4时,y=9;当x=6时,y=﹣1,
∴,
解得:,
故这个一次函数的解析式为y=﹣5x+29;
(2)把x=1代入y=﹣5x+29中得:y=﹣5+29=24.
22.已知:如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
【解答】证明:∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵EF⊥DF,
∴∠EFD=90°,
∴∠EFB+∠DFC=90°,∠DFC+∠FDC=90°,
∴∠EFB=∠DFC,
∵BE=CF,
∴△BEF≌△CFD,
∴BF=CD.
23.某校举行以“建党一百周年”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表.
分数段 频数 频率
60≤x<70 30 0.15
70≤x<80 m 0.45
80≤x<90 60 n
90≤x<100 20 0.1
请根据图表提供的信息,解答下列问题.
(1)求表中m和n所表示的数;
(2)请在图中补全频数分别直方图;
(3)若比赛成绩不低于80分可以获奖,则获奖率为多少?
解:(1)样本容量==200,
所以m=200×0.45=90,
n==0.3;
(2)如图:
(3)读图表可得比赛成绩不低于80分的人数为60+20=80,
故获奖率为×100%=40%.
24.如图,在△ABC中,∠ACB=90°,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
(1)求证:四边形ECBF是平行四边形;
(2)当∠A=30°时,求证:四边形ECBF是菱形.
【解答】证明:(1)∵D,E分别为边AC,AB的中点,
∴DE∥BC,即EF∥BC.
又∵BF∥CE,
∴四边形ECBF是平行四边形.
(2)∵∠ACB=90°,∠A=30°,E为AB的中点,
∴CB=AB,CE=AB.
∴CB=CE.
又由(1)知,四边形ECBF是平行四边形,
∴四边形ECBF是菱形.
25.如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm.求:
(1)两条对角线的长度;
(2)菱形的面积.
解:(1)∵四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC与∠BAD的度数比为1:2,
∴∠ABC=×180°=60°,
∴∠ABO=∠ABC=30°,
∵菱形ABCD的周长是8cm.
∴AB=2cm,
∴OA=AB=1cm,
∴OB==,
∴AC=2OA=2cm,BD=2OB=2cm;
(2)S菱形ABCD=AC?BD=×2×2=2(cm2).
26.我国传统的计重工具﹣﹣秤的应用,方便了人们的生活.如图1,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量.称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数.下表中为若干次称重时所记录的一些数据.
x(厘米) 1 2 4 7 11 12
y(斤) 0.75 1.00 1.50 2.75 3.25 3.50
(1)在上表x,y的数据中,发现有一对数据记录错误.在图2中,通过描点的方法,观察判断哪一对是错误的?
(2)根据(1)的发现,问秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少?
解:(1)观察图象可知:x=7,y=2.75这组数据错误.
(2)设y=kx+b,把x=1,y=0.75,x=2,y=1代入可得,
解得,
∴y=x+,
当x=16时,y=4.5,
答:秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是4.5斤.
27.如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
(1)如图1,求证:△BCP≌△DCQ;
(2)如图,延长BP交直线DQ于点E.
①如图2,求证:BE⊥DQ;
②如图3,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
【解答】(1)证明:∵∠BCD=90°,∠PCQ=90°,
∴∠BCP=∠DCQ,
在△BCP和△DCQ中,
,
∴△BCP≌△DCQ(SAS);
(2)①如图b,∵△BCP≌△DCQ,
∴∠CBF=∠EDF,又∠BFC=∠DFE,
∴∠DEF=∠BCF=90°,
∴BE⊥DQ;
②∵△BCP为等边三角形,
∴∠BCP=60°,
∴∠PCD=30°,又CP=CD,
∴∠CPD=∠CDP=75°,又∠BPC=60°,∠CDQ=60°,
∴∠EPD=180°﹣∠CPD﹣∠CPB=180°﹣75°﹣60=45°,
同理:∠EDP=45°,
∴△DEP为等腰直角三角形.
一、选择题(每小题3分,共30分)
1.下列既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.直线y=x﹣1的图象经过( )
A.第二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第一、二、三象限
3.在平面直角坐标系中,点P(﹣1,﹣2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.五边形的内角和为( )
A.360° B.540° C.720° D.900°
5.菱形具有而平行四边形不一定具有的性质是( )
A.两组对边分别平行 B.两组对角分别相等
C.对角线互相平分 D.对角线互相垂直
6.顺次连接矩形四边中点所得的四边形一定是( )
A.正方形 B.矩形 C.菱形 D.等腰梯形
7.一个三角形的周长是36cm,则以这个三角形各边中点为顶点的三角形的周长是( )
A.6cm B.12cm C.18cm D.36cm
8.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B.5 C.4 D.7
9.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是( )
A. B.
C. D.
10.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( )
A. B.3 C.1 D.
二、填空题(每小题3分,共30分)
11.已知点P(﹣1,1)关于x轴的对称点Q的坐标为 .
12.将直线y=3x向上平移3个单位,得到直线 .
13.某班50位同学中,1月份出生的频率是0.30,这个班1月份出生的同学有 人.
14.若正比例函数y=kx的图象经过点(1,2),则k= .
15.已知菱形ABCD的面积为24cm2,若对角线AC=6cm,则这个菱形的边长为 cm.
16.已知△ABC的三边长分别为1,,2,则△ABC是 三角形.
17.已知一次函数y=(1﹣m)x+1,当m 时,y随x的增大而增大.
18.若点M(a﹣2,2a+3)是y轴上的点,则a的值为 .
19.如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,则△ABC的周长是 .
20.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为 .
三、解答题:(共60分)
21.已知y是x的一次函数,且当x=4时,y=9;当x=6时,y=﹣1.
(1)求这个一次函数的表达式;
(2)当x=1时,求y的值.
22.已知:如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
23.某校举行以“建党一百周年”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表.
分数段 频数 频率
60≤x<70 30 0.15
70≤x<80 m 0.45
80≤x<90 60 n
90≤x<100 20 0.1
请根据图表提供的信息,解答下列问题.
(1)求表中m和n所表示的数;
(2)请在图中补全频数分别直方图;
(3)若比赛成绩不低于80分可以获奖,则获奖率为多少?
24.如图,在△ABC中,∠ACB=90°,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
(1)求证:四边形ECBF是平行四边形;
(2)当∠A=30°时,求证:四边形ECBF是菱形.
25.如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm.求:
(1)两条对角线的长度;
(2)菱形的面积.
26.我国传统的计重工具﹣﹣秤的应用,方便了人们的生活.如图1,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量.称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数.下表中为若干次称重时所记录的一些数据.
x(厘米) 1 2 4 7 11 12
y(斤) 0.75 1.00 1.50 2.75 3.25 3.50
(1)在上表x,y的数据中,发现有一对数据记录错误.在图2中,通过描点的方法,观察判断哪一对是错误的?
(2)根据(1)的发现,问秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少?
27.如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
(1)如图1,求证:△BCP≌△DCQ;
(2)如图,延长BP交直线DQ于点E.
①如图2,求证:BE⊥DQ;
②如图3,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
参考答案
一、选择题(每小题3分,共30分)
1.下列既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
解:A、是轴对称图形,也是中心对称图形;
B、是轴对称图形,不是中心对称图形;
C、是轴对称图形,不是中心对称图形;
D、不是轴对称图形,也不是中心对称图形.
故选:A.
2.直线y=x﹣1的图象经过( )
A.第二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第一、二、三象限
解:直线y=x﹣1与y轴交于(0,﹣1)点,
且k=1>0,y随x的增大而增大,
∴直线y=x﹣1的图象经过第一、三、四象限.
故选:C.
3.在平面直角坐标系中,点P(﹣1,﹣2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:点P(﹣1,﹣2),由横纵坐标均为负数,则此点在第三象限.
故选:C.
4.五边形的内角和为( )
A.360° B.540° C.720° D.900°
解:五边形的内角和是(5﹣2)×180°=540°.故选:B.
5.菱形具有而平行四边形不一定具有的性质是( )
A.两组对边分别平行 B.两组对角分别相等
C.对角线互相平分 D.对角线互相垂直
解:A、不正确,两组对边分别平行;
B、不正确,两组对角分别相等,两者均有此性质正确,;
C、不正确,对角线互相平分,两者均具有此性质;
D、菱形的对角线互相垂直但平行四边形却无此性质.
故选:D.
6.顺次连接矩形四边中点所得的四边形一定是( )
A.正方形 B.矩形 C.菱形 D.等腰梯形
解:连接AC、BD,
在△ABD中,
∵AH=HD,AE=EB
∴EH=BD,
同理FG=BD,HG=AC,EF=AC,
又∵在矩形ABCD中,AC=BD,
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.
故选:C.
7.一个三角形的周长是36cm,则以这个三角形各边中点为顶点的三角形的周长是( )
A.6cm B.12cm C.18cm D.36cm
解:如图,点D、E、F分别是AB、AC、BC的中点,
∴DE=BC,DF=AC,EF=AB,
∵原三角形的周长为36cm,
则新三角形的周长为=18(cm).
故选:C.
8.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B.5 C.4 D.7
解:作EF⊥BC于F,
∵BE平分∠ABC,EF⊥BC,ED⊥AB,
∴EF=DE=2,
∴△BCE的面积=×BC×EF=5.
故选:B.
9.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是( )
A. B.
C. D.
解:当点P由点A向点D运动,即0<x≤4时,y的值为0;
当点P在DC上运动,即4<x≤8时,y随着x的增大而增大;
当点P在CB上运动,即8<x≤12时,y不变;
当点P在BA上运动,即12<x≤16时,y随x的增大而减小.
故选:B.
10.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( )
A. B.3 C.1 D.
解:∵AB=3,AD=4,
∴DC=3,
∴AC==5,
根据折叠可得:△DEC≌△D′EC,
∴D′C=DC=3,DE=D′E,
设ED=x,则D′E=x,AD′=AC﹣CD′=2,AE=4﹣x,
在Rt△AED′中:(AD′)2+(ED′)2=AE2,
22+x2=(4﹣x)2,
解得:x=,
故选:A.
二、填空题(每小题3分,共30分)
11.已知点P(﹣1,1)关于x轴的对称点Q的坐标为 (﹣1,﹣1) .
解:点P(﹣1,1)关于x轴的对称点Q的坐标为:(﹣1,﹣1).
故答案为:(﹣1,﹣1).
12.将直线y=3x向上平移3个单位,得到直线 y=3x+3 .
解:将直线y=3x向上平移3个单位,得到直线:y=3x+3.
故答案为y=3x+3.
13.某班50位同学中,1月份出生的频率是0.30,这个班1月份出生的同学有 15 人.
解:50×0.30=15(人),
故答案为:15.
14.若正比例函数y=kx的图象经过点(1,2),则k= 2 .
解:∵正比例函数y=kx的图象经过点(1,2),
∴2=k×1,即k=2.
故答案为:2.
15.已知菱形ABCD的面积为24cm2,若对角线AC=6cm,则这个菱形的边长为 5 cm.
解:菱形ABCD的面积=AC?BD,
∵菱形ABCD的面积是24cm2,其中一条对角线AC长6cm,
∴另一条对角线BD的长=8cm;
边长是:=5cm.
故答案为:5.
16.已知△ABC的三边长分别为1,,2,则△ABC是 直角 三角形.
解:∵12+()2=22,
∴△ABC是直角三角形.
故答案为:直角.
17.已知一次函数y=(1﹣m)x+1,当m <1 时,y随x的增大而增大.
解:当1﹣m>0时,y随x的增大而增大,
所以m<1.
故答案为:<1.
18.若点M(a﹣2,2a+3)是y轴上的点,则a的值为 2 .
解:∵点M(a﹣2,2a+3)是y轴上的点,
∴a﹣2=0,
解得a=2.
故答案为:2.
19.如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,则△ABC的周长是 25 .
解:延长线段BN交AC于E.
∵AN平分∠BAC,
∴∠BAN=∠EAN,
∵BN⊥AN,
∴∠ANB=∠ANE=90°,
在△ABN和△AEN中,
,
∴△ABN≌△AEN(ASA),
∴AE=AB=6,BN=NE,
又∵M是△ABC的边BC的中点,
∴CE=2MN=2×1.5=3,
∴△ABC的周长是AB+BC+AC=6+10+6+3=25,
故答案为:25.
20.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为 .
解:连接CM,如图所示:
∵MD⊥AC,ME⊥CB,
∴∠MDC=∠MEC=90°,
∵∠C=90°,
∴四边形CDME是矩形,
∴DE=CM,
∵∠C=90°,BC=3,AC=4,
∴AB===5,
当CM⊥AB时,CM最短,此时△ABC的面积=AB?CM=BC?AC,
∴CM的最小值==,
∴线段DE的最小值为;
故答案为:.
三、解答题:(共60分)
21.已知y是x的一次函数,且当x=4时,y=9;当x=6时,y=﹣1.
(1)求这个一次函数的表达式;
(2)当x=1时,求y的值.
解:(1)设这个一次函数的解析式为y=kx+b(k≠0),
∵当x=4时,y=9;当x=6时,y=﹣1,
∴,
解得:,
故这个一次函数的解析式为y=﹣5x+29;
(2)把x=1代入y=﹣5x+29中得:y=﹣5+29=24.
22.已知:如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
【解答】证明:∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵EF⊥DF,
∴∠EFD=90°,
∴∠EFB+∠DFC=90°,∠DFC+∠FDC=90°,
∴∠EFB=∠DFC,
∵BE=CF,
∴△BEF≌△CFD,
∴BF=CD.
23.某校举行以“建党一百周年”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表.
分数段 频数 频率
60≤x<70 30 0.15
70≤x<80 m 0.45
80≤x<90 60 n
90≤x<100 20 0.1
请根据图表提供的信息,解答下列问题.
(1)求表中m和n所表示的数;
(2)请在图中补全频数分别直方图;
(3)若比赛成绩不低于80分可以获奖,则获奖率为多少?
解:(1)样本容量==200,
所以m=200×0.45=90,
n==0.3;
(2)如图:
(3)读图表可得比赛成绩不低于80分的人数为60+20=80,
故获奖率为×100%=40%.
24.如图,在△ABC中,∠ACB=90°,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
(1)求证:四边形ECBF是平行四边形;
(2)当∠A=30°时,求证:四边形ECBF是菱形.
【解答】证明:(1)∵D,E分别为边AC,AB的中点,
∴DE∥BC,即EF∥BC.
又∵BF∥CE,
∴四边形ECBF是平行四边形.
(2)∵∠ACB=90°,∠A=30°,E为AB的中点,
∴CB=AB,CE=AB.
∴CB=CE.
又由(1)知,四边形ECBF是平行四边形,
∴四边形ECBF是菱形.
25.如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm.求:
(1)两条对角线的长度;
(2)菱形的面积.
解:(1)∵四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC与∠BAD的度数比为1:2,
∴∠ABC=×180°=60°,
∴∠ABO=∠ABC=30°,
∵菱形ABCD的周长是8cm.
∴AB=2cm,
∴OA=AB=1cm,
∴OB==,
∴AC=2OA=2cm,BD=2OB=2cm;
(2)S菱形ABCD=AC?BD=×2×2=2(cm2).
26.我国传统的计重工具﹣﹣秤的应用,方便了人们的生活.如图1,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量.称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数.下表中为若干次称重时所记录的一些数据.
x(厘米) 1 2 4 7 11 12
y(斤) 0.75 1.00 1.50 2.75 3.25 3.50
(1)在上表x,y的数据中,发现有一对数据记录错误.在图2中,通过描点的方法,观察判断哪一对是错误的?
(2)根据(1)的发现,问秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少?
解:(1)观察图象可知:x=7,y=2.75这组数据错误.
(2)设y=kx+b,把x=1,y=0.75,x=2,y=1代入可得,
解得,
∴y=x+,
当x=16时,y=4.5,
答:秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是4.5斤.
27.如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
(1)如图1,求证:△BCP≌△DCQ;
(2)如图,延长BP交直线DQ于点E.
①如图2,求证:BE⊥DQ;
②如图3,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
【解答】(1)证明:∵∠BCD=90°,∠PCQ=90°,
∴∠BCP=∠DCQ,
在△BCP和△DCQ中,
,
∴△BCP≌△DCQ(SAS);
(2)①如图b,∵△BCP≌△DCQ,
∴∠CBF=∠EDF,又∠BFC=∠DFE,
∴∠DEF=∠BCF=90°,
∴BE⊥DQ;
②∵△BCP为等边三角形,
∴∠BCP=60°,
∴∠PCD=30°,又CP=CD,
∴∠CPD=∠CDP=75°,又∠BPC=60°,∠CDQ=60°,
∴∠EPD=180°﹣∠CPD﹣∠CPB=180°﹣75°﹣60=45°,
同理:∠EDP=45°,
∴△DEP为等腰直角三角形.
同课章节目录
