沪科版2021年八年级上册:第14章 全等三角形 测试卷(word版,含答案)
文档属性
| 名称 | 沪科版2021年八年级上册:第14章 全等三角形 测试卷(word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 817.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 02:18:55 | ||
图片预览



文档简介
第14章 测试卷
一、选择题(每题3分,共30分)
1.如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAC=25°,则∠BAE的度数为( )
A.55° B.75° C.105° D.115°
(第1题) (第3题) (第4题)
2.下列结论不正确的是( )
A.两个锐角对应相等的两个直角三角形全等
B.一锐角和斜边对应相等的两个直角三角形全等
C.一直角边和一锐角对应相等的两个直角三角形全等
D.两条直角边对应相等的两个直角三角形全等
3.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A.两点之间线段最短 B.三角形具有稳定性
C.长方形是轴对称图形 D.长方形的四个角都是直角
4.根据下列条件,能画出唯一△ABC的是( )
A.AB=3,BC=4,CA=7
B.AC=4,BC=3.5,∠A=60°
C.∠A=45°,∠B=60°,∠C=75°
D.AB=5,BC=4,∠C=90°
5.△ABC的六个元素如图①所示,则图②中的三角形与△ABC全等的是( )
(第5题)
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
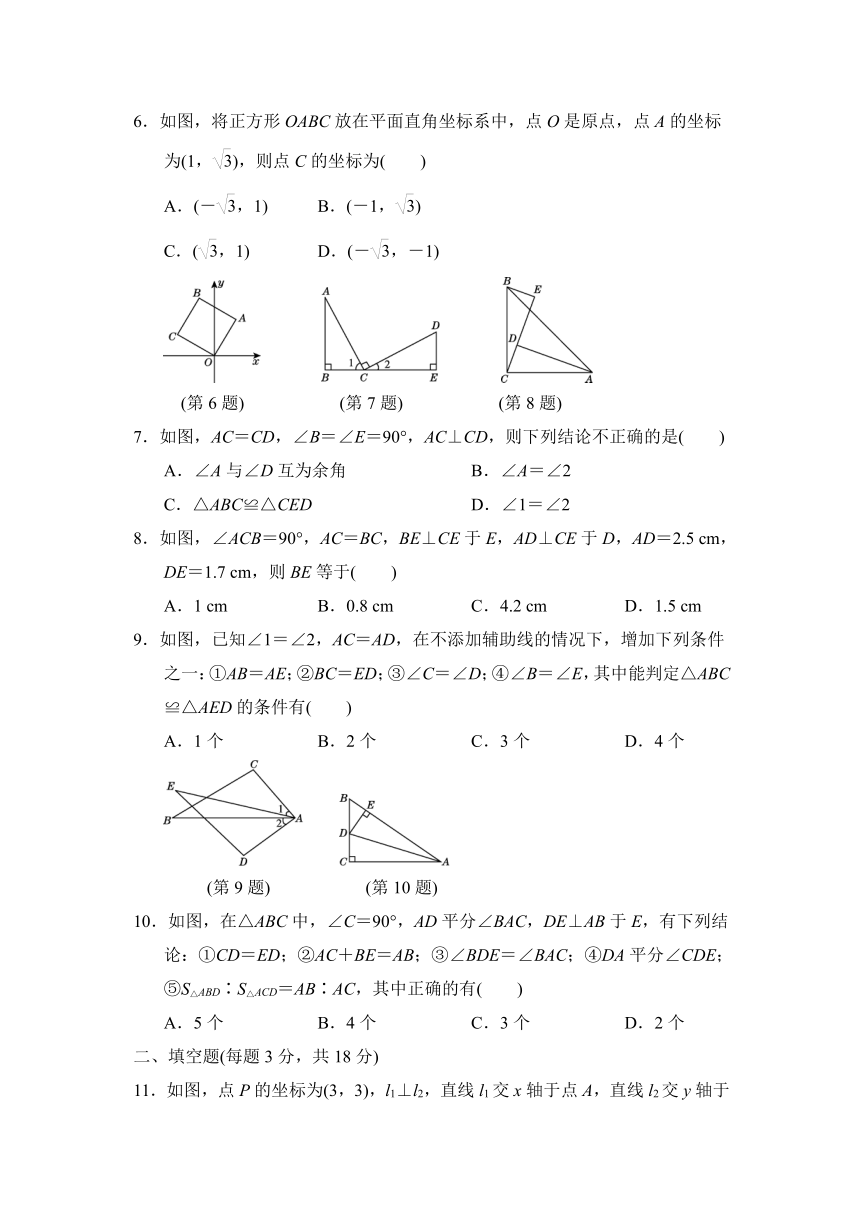
6.如图,将正方形OABC放在平面直角坐标系中,点O是原点,点A的坐标为(1,),则点C的坐标为( )
A.(-,1) B.(-1,)
C.(,1) D.(-,-1)
(第6题) (第7题) (第8题)
7.如图,AC=CD,∠B=∠E=90°,AC⊥CD,则下列结论不正确的是( )
A.∠A与∠D互为余角 B.∠A=∠2
C.△ABC≌△CED D.∠1=∠2
8.如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=2.5 cm,DE=1.7 cm,则BE等于( )
A.1 cm B.0.8 cm C.4.2 cm D.1.5 cm
9.如图,已知∠1=∠2,AC=AD,在不添加辅助线的情况下,增加下列条件之一:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E,其中能判定△ABC≌△AED的条件有( )
A.1个 B.2个 C.3个 D.4个
(第9题) (第10题)
10.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④DA平分∠CDE;⑤S△ABD∶S△ACD=AB∶AC,其中正确的有( )
A.5个 B.4个 C.3个 D.2个
二、填空题(每题3分,共18分)
11.如图,点P的坐标为(3,3),l1⊥l2,直线l1交x轴于点A,直线l2交y轴于点B,则四边形OAPB的面积为________.
(第11题) (第12题) (第13题)
12.如图,在△ABC中,点A(0,1),点B(0,4),点C(4,3),如果要使△ABD与△ABC全等(C与D不重合),那么点D的坐标是________________________.
13.如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E、F,连接CE、BF.添加一个条件,使得△BDF≌△CDE.你添加的条件是____________.(不添加辅助线)
14.如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有________对全等三角形.
(第14题) (第15题) (第16题)
15.如图,在△ABC中,已知∠CAB=60°,D,E分别是边AB,AC上的点,且∠AED=60°,ED+DB=CE,∠CDB=2∠CDE,则∠DCB等于________.
16.如图,CA⊥AB,垂足为点A,AB=8厘米,AC=4厘米,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着点E运动而运动,且始终保持ED=CB,当点E离开点A后,运动________________________时,△DEB与△BCA全等.
三、解答题(17题6分,18,19题每题8分,其余每题10分,共52分)
17.如图,在新修的小区中,有一条“Z”字形绿色长廊ABCD,其中AB∥CD,在AB,BC,CD三段绿色长廊上各修一小凉亭E,M,F,且BE=CF,点M是BC的中点,在凉亭M与F之间有一池塘,不能直接到达,要想知道M与F之间的距离,只需要测出线段ME的长度,这样做合适吗?请说明理由.
(第17题)
18.如图,在四边形ABCD中,AD∥BC,E为AC的中点,连接DE并延长,交BC于点F.
(1)求证:DE=EF;
(2)若AD=12,BF∶CF=2∶3,求BC的长.
(第18题)
19.如图,在四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F.
(1)求证:△ABE≌△BCD;
(2)判断线段AE与BD的数量关系及位置关系,并说明理由.
(第19题)
20.如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
(第20题)
21.如图,在△AEC和△DFB中,∠E=∠F,∠E>90°,点A,B,C,D在同一直线上,有如下三个关系式:①AE∥DF,②AB=CD,③CE=BF.
(1)请用其中两个关系式作为条件,第三个作为结论,写出你认为正确的所有命题(用序号写出命题书写形式:“如果??,那么?”);
(2)选择(1)中你写出的一个命题,说明它正确的理由.
(第21题)
22. 如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,交CB的延长线于F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.
(第22题)
答案
一、1.D 2.A 3.B 4.D 5.B
6.A 过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,∵四边形OABC是正方形,∴OA=OC,∠AOC=90°.∴∠COE+∠AOD=90°.又∵∠OAD+∠AOD=90°,∴∠OAD=∠COE.在△AOD和△OCE中,∠OAD=∠COE,∠ADO=∠OEC=90°,OA=CO,∴△AOD≌△OCE(AAS),∴OE=AD=,CE=OD=1.∵点C在第二象限,∴点C的坐标为(-,1).故选A.
7.D
8.B ∵BE⊥CE,AD⊥CE,∴∠E=∠ADC=90°,∴∠CAD+∠ACD=90°.∵∠ACB=90°,∴∠BCE+∠ACD=90°,∴∠BCE=∠CAD.又∵BC=CA,∴△BCE≌△CAD(AAS),∴CE=AD,BE=CD.∵AD=2.5 cm,DE=1.7 cm,∴BE=CD=CE-DE=2.5-1.7=0.8(cm).
9.C 10.A
二、11.9 过P分别作x轴和y轴的垂线,交x轴和y轴于点C和D,则∠PDB=∠PCA=90°.∵点P的坐标为(3,3),∴PC=PD.∵l1⊥l2,∴∠BPA=90°.又∵∠DPC=90°,∴∠DPB=∠CPA,∴△PDB≌△PCA(ASA),∴S△PDB=S△PCA,∴S四边形OAPB=S正方形ODPC=3×3=9.
12.(4,2)或(-4,2)或(-4,3) 13.DE=DF(答案不唯一)
14.3 15.20° 16.2秒或6秒或8秒
三、17.解:合适.理由:∵AB∥CD,∴∠B=∠C.
∵点M是BC的中点,∴BM=CM.
在△BEM与△CFM中,∵
∴△BEM≌△CFM(SAS).∴EM=FM.∴只需要测出线段ME的长度就可以知道M与F之间的距离.
18.(1)证明:∵AD∥BC,∴∠DAE=∠FCE,∠ADE=∠EFC.
∵E为AC的中点,∴AE=CE.
在△ADE和△CFE中,
∴△ADE≌△CFE(AAS).∴DE=EF.
(2)解:由(1)知△ADE≌△CFE,∴AD=CF=12,
∵BF∶CF=2∶3,∴BF=8,
∴BC=BF+CF=8+12=20.
19.(1)证明:∵AB∥CD,∴∠ABE+∠C=180°,
∵∠C=90°,∴∠ABE=90°=∠C,
∵E是BC的中点,∴BC=2BE,
∵BC=2CD,∴BE=CD,
在△ABE和△BCD中,∴△ABE≌△BCD(SAS).
(2)解:AE=BD,AE⊥BD.
理由:由(1)得△ABE≌△BCD,∴AE=BD,∠BAE=∠CBD,
∵∠ABF+∠CBD=90°,∴∠ABF+∠BAE=90°,
∴∠AFB=90°,∴AE⊥BD.
20.(1)证明:∵将线段CD绕点C按顺时针方向旋转90°后得CE,∴CD=CE,∠DCE=90°.
∵∠ACB=90°,∴∠BCD=90°-∠ACD=∠FCE.
在△BCD和△FCE中,∵∴△BCD≌△FCE(SAS).
(2)解:由(1)可知△BCD≌△FCE,∴∠BDC=∠E.
∵EF∥CD,∴∠E=180°-∠DCE=90°,∴∠BDC=90°.
21.解:(1)命题1:如果①②,那么③;命题2:如果①③,那么②;命题3:如果②③,那么①.
(2)命题1正确的理由如下:∵①AE∥DF,∴∠A=∠D.
∵②AB=CD,∴AB+BC=CD+BC,即AC=DB.
在△AEC和△DFB中,∵∠E=∠F,∠A=∠D,AC=DB,
∴△AEC≌△DFB(AAS).∴③CE=BF(全等三角形的对应边相等).
(2)题答案不唯一.
22.(1)证明:∵∠BAD=∠CAE=90°,∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,∴∠BAC=∠DAE,
在△ABC和△ADE中,∵∴△ABC≌△ADE.
(2)解:∵∠CAE=90°,AC=AE,∴∠E=45°.
由(1)知△ABC≌△ADE,∴∠BCA=∠E=45°.
∵AF⊥BC,∴∠CFA=90°,∴∠CAF=45°.
∴∠FAE=∠CAF+∠CAE=45°+90°=135°.
(3)证明:延长BF到G,使得FG=FB,连接AG.
∵AF⊥BC,∴∠AFG=∠AFB=90°.
在△AFB和△AFG中,∵
∴△AFB≌△AFG.∴AB=AG,∠ABF=∠G.∵AB=AD,∴AG=AD.∵△ABC≌△ADE,∴∠CBA=∠EDA,CB=ED,
∴∠ABF=∠CDA,∴∠G=∠CDA.
由题意易得∠GCA=∠DCA=45°,
在△CGA和△CDA中,∵∴△CGA≌△CDA,
∴CG=CD.∵CG=CB+BF+FG=CB+2BF=DE+2BF,
∴CD=2BF+DE.
一、选择题(每题3分,共30分)
1.如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAC=25°,则∠BAE的度数为( )
A.55° B.75° C.105° D.115°
(第1题) (第3题) (第4题)
2.下列结论不正确的是( )
A.两个锐角对应相等的两个直角三角形全等
B.一锐角和斜边对应相等的两个直角三角形全等
C.一直角边和一锐角对应相等的两个直角三角形全等
D.两条直角边对应相等的两个直角三角形全等
3.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A.两点之间线段最短 B.三角形具有稳定性
C.长方形是轴对称图形 D.长方形的四个角都是直角
4.根据下列条件,能画出唯一△ABC的是( )
A.AB=3,BC=4,CA=7
B.AC=4,BC=3.5,∠A=60°
C.∠A=45°,∠B=60°,∠C=75°
D.AB=5,BC=4,∠C=90°
5.△ABC的六个元素如图①所示,则图②中的三角形与△ABC全等的是( )
(第5题)
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
6.如图,将正方形OABC放在平面直角坐标系中,点O是原点,点A的坐标为(1,),则点C的坐标为( )
A.(-,1) B.(-1,)
C.(,1) D.(-,-1)
(第6题) (第7题) (第8题)
7.如图,AC=CD,∠B=∠E=90°,AC⊥CD,则下列结论不正确的是( )
A.∠A与∠D互为余角 B.∠A=∠2
C.△ABC≌△CED D.∠1=∠2
8.如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=2.5 cm,DE=1.7 cm,则BE等于( )
A.1 cm B.0.8 cm C.4.2 cm D.1.5 cm
9.如图,已知∠1=∠2,AC=AD,在不添加辅助线的情况下,增加下列条件之一:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E,其中能判定△ABC≌△AED的条件有( )
A.1个 B.2个 C.3个 D.4个
(第9题) (第10题)
10.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④DA平分∠CDE;⑤S△ABD∶S△ACD=AB∶AC,其中正确的有( )
A.5个 B.4个 C.3个 D.2个
二、填空题(每题3分,共18分)
11.如图,点P的坐标为(3,3),l1⊥l2,直线l1交x轴于点A,直线l2交y轴于点B,则四边形OAPB的面积为________.
(第11题) (第12题) (第13题)
12.如图,在△ABC中,点A(0,1),点B(0,4),点C(4,3),如果要使△ABD与△ABC全等(C与D不重合),那么点D的坐标是________________________.
13.如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E、F,连接CE、BF.添加一个条件,使得△BDF≌△CDE.你添加的条件是____________.(不添加辅助线)
14.如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有________对全等三角形.
(第14题) (第15题) (第16题)
15.如图,在△ABC中,已知∠CAB=60°,D,E分别是边AB,AC上的点,且∠AED=60°,ED+DB=CE,∠CDB=2∠CDE,则∠DCB等于________.
16.如图,CA⊥AB,垂足为点A,AB=8厘米,AC=4厘米,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着点E运动而运动,且始终保持ED=CB,当点E离开点A后,运动________________________时,△DEB与△BCA全等.
三、解答题(17题6分,18,19题每题8分,其余每题10分,共52分)
17.如图,在新修的小区中,有一条“Z”字形绿色长廊ABCD,其中AB∥CD,在AB,BC,CD三段绿色长廊上各修一小凉亭E,M,F,且BE=CF,点M是BC的中点,在凉亭M与F之间有一池塘,不能直接到达,要想知道M与F之间的距离,只需要测出线段ME的长度,这样做合适吗?请说明理由.
(第17题)
18.如图,在四边形ABCD中,AD∥BC,E为AC的中点,连接DE并延长,交BC于点F.
(1)求证:DE=EF;
(2)若AD=12,BF∶CF=2∶3,求BC的长.
(第18题)
19.如图,在四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F.
(1)求证:△ABE≌△BCD;
(2)判断线段AE与BD的数量关系及位置关系,并说明理由.
(第19题)
20.如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
(第20题)
21.如图,在△AEC和△DFB中,∠E=∠F,∠E>90°,点A,B,C,D在同一直线上,有如下三个关系式:①AE∥DF,②AB=CD,③CE=BF.
(1)请用其中两个关系式作为条件,第三个作为结论,写出你认为正确的所有命题(用序号写出命题书写形式:“如果??,那么?”);
(2)选择(1)中你写出的一个命题,说明它正确的理由.
(第21题)
22. 如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,交CB的延长线于F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.
(第22题)
答案
一、1.D 2.A 3.B 4.D 5.B
6.A 过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,∵四边形OABC是正方形,∴OA=OC,∠AOC=90°.∴∠COE+∠AOD=90°.又∵∠OAD+∠AOD=90°,∴∠OAD=∠COE.在△AOD和△OCE中,∠OAD=∠COE,∠ADO=∠OEC=90°,OA=CO,∴△AOD≌△OCE(AAS),∴OE=AD=,CE=OD=1.∵点C在第二象限,∴点C的坐标为(-,1).故选A.
7.D
8.B ∵BE⊥CE,AD⊥CE,∴∠E=∠ADC=90°,∴∠CAD+∠ACD=90°.∵∠ACB=90°,∴∠BCE+∠ACD=90°,∴∠BCE=∠CAD.又∵BC=CA,∴△BCE≌△CAD(AAS),∴CE=AD,BE=CD.∵AD=2.5 cm,DE=1.7 cm,∴BE=CD=CE-DE=2.5-1.7=0.8(cm).
9.C 10.A
二、11.9 过P分别作x轴和y轴的垂线,交x轴和y轴于点C和D,则∠PDB=∠PCA=90°.∵点P的坐标为(3,3),∴PC=PD.∵l1⊥l2,∴∠BPA=90°.又∵∠DPC=90°,∴∠DPB=∠CPA,∴△PDB≌△PCA(ASA),∴S△PDB=S△PCA,∴S四边形OAPB=S正方形ODPC=3×3=9.
12.(4,2)或(-4,2)或(-4,3) 13.DE=DF(答案不唯一)
14.3 15.20° 16.2秒或6秒或8秒
三、17.解:合适.理由:∵AB∥CD,∴∠B=∠C.
∵点M是BC的中点,∴BM=CM.
在△BEM与△CFM中,∵
∴△BEM≌△CFM(SAS).∴EM=FM.∴只需要测出线段ME的长度就可以知道M与F之间的距离.
18.(1)证明:∵AD∥BC,∴∠DAE=∠FCE,∠ADE=∠EFC.
∵E为AC的中点,∴AE=CE.
在△ADE和△CFE中,
∴△ADE≌△CFE(AAS).∴DE=EF.
(2)解:由(1)知△ADE≌△CFE,∴AD=CF=12,
∵BF∶CF=2∶3,∴BF=8,
∴BC=BF+CF=8+12=20.
19.(1)证明:∵AB∥CD,∴∠ABE+∠C=180°,
∵∠C=90°,∴∠ABE=90°=∠C,
∵E是BC的中点,∴BC=2BE,
∵BC=2CD,∴BE=CD,
在△ABE和△BCD中,∴△ABE≌△BCD(SAS).
(2)解:AE=BD,AE⊥BD.
理由:由(1)得△ABE≌△BCD,∴AE=BD,∠BAE=∠CBD,
∵∠ABF+∠CBD=90°,∴∠ABF+∠BAE=90°,
∴∠AFB=90°,∴AE⊥BD.
20.(1)证明:∵将线段CD绕点C按顺时针方向旋转90°后得CE,∴CD=CE,∠DCE=90°.
∵∠ACB=90°,∴∠BCD=90°-∠ACD=∠FCE.
在△BCD和△FCE中,∵∴△BCD≌△FCE(SAS).
(2)解:由(1)可知△BCD≌△FCE,∴∠BDC=∠E.
∵EF∥CD,∴∠E=180°-∠DCE=90°,∴∠BDC=90°.
21.解:(1)命题1:如果①②,那么③;命题2:如果①③,那么②;命题3:如果②③,那么①.
(2)命题1正确的理由如下:∵①AE∥DF,∴∠A=∠D.
∵②AB=CD,∴AB+BC=CD+BC,即AC=DB.
在△AEC和△DFB中,∵∠E=∠F,∠A=∠D,AC=DB,
∴△AEC≌△DFB(AAS).∴③CE=BF(全等三角形的对应边相等).
(2)题答案不唯一.
22.(1)证明:∵∠BAD=∠CAE=90°,∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,∴∠BAC=∠DAE,
在△ABC和△ADE中,∵∴△ABC≌△ADE.
(2)解:∵∠CAE=90°,AC=AE,∴∠E=45°.
由(1)知△ABC≌△ADE,∴∠BCA=∠E=45°.
∵AF⊥BC,∴∠CFA=90°,∴∠CAF=45°.
∴∠FAE=∠CAF+∠CAE=45°+90°=135°.
(3)证明:延长BF到G,使得FG=FB,连接AG.
∵AF⊥BC,∴∠AFG=∠AFB=90°.
在△AFB和△AFG中,∵
∴△AFB≌△AFG.∴AB=AG,∠ABF=∠G.∵AB=AD,∴AG=AD.∵△ABC≌△ADE,∴∠CBA=∠EDA,CB=ED,
∴∠ABF=∠CDA,∴∠G=∠CDA.
由题意易得∠GCA=∠DCA=45°,
在△CGA和△CDA中,∵∴△CGA≌△CDA,
∴CG=CD.∵CG=CB+BF+FG=CB+2BF=DE+2BF,
∴CD=2BF+DE.
