2.2.1综合法
图片预览




文档简介
(共17张PPT)
2.2直接证明与间接证明
2.2.1 综合法
熊德忠
12.5.19
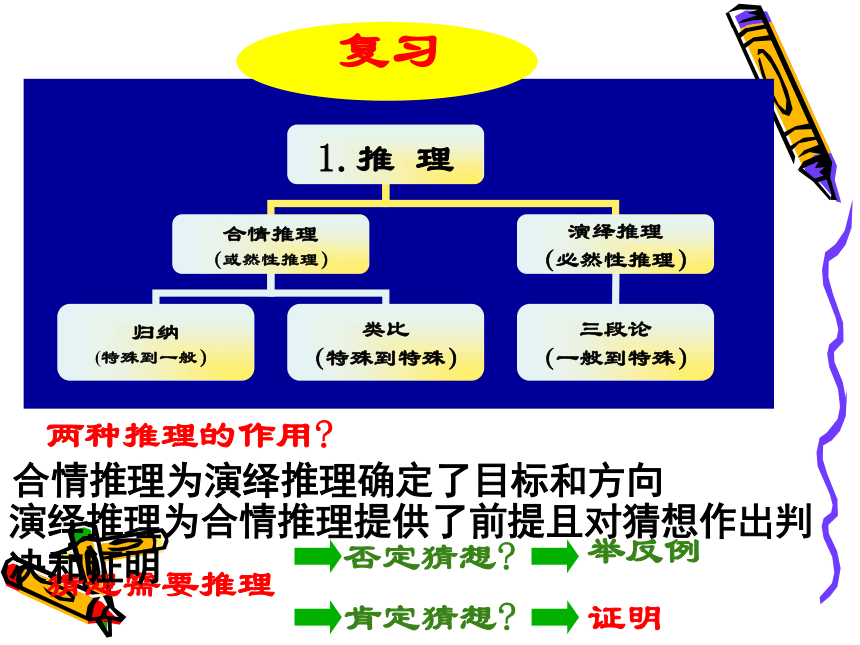
两种推理的作用
1.推 理
合情推理
(或然性推理)
演绎推理
(必然性推理)
归纳
(特殊到一般)
类比
(特殊到特殊)
三段论
(一般到特殊)
复习
猜想需要推理
否定猜想
肯定猜想
举反例
证明
合情推理为演绎推理确定了目标和方向
演绎推理为合情推理提供了前提且对猜想作出判决和证明
温故夯基
归纳
类比
大前提
小前提
结论.
充分不必要
1
2
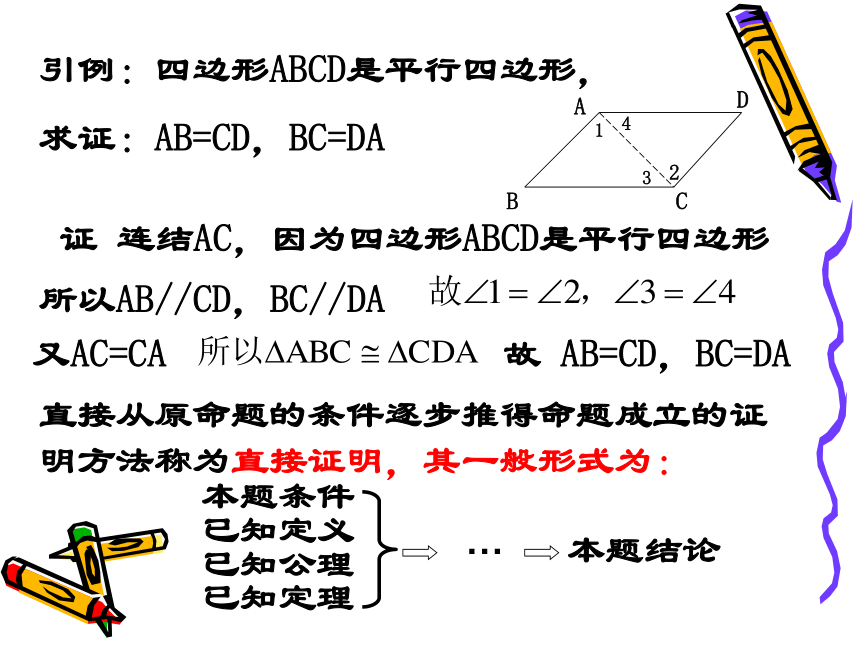
引例:四边形ABCD是平行四边形,
求证:AB=CD,BC=DA
A
B
C
D
1
3
4
2
证 连结AC,因为四边形ABCD是平行四边形
所以AB//CD,BC//DA
又AC=CA
故 AB=CD,BC=DA
直接从原命题的条件逐步推得命题成立的证明方法称为直接证明,其一般形式为:
本题条件
已知定义
已知定理
已知公理
本题结论
…
学习目标
1.了解直接证明的两种基本方法——综合法和分析法.
2.理解综合法和分析法的思考过程、特点,会用综合法和分析法证明数学问题.
例1:已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc
因为b2+c2 ≥2bc,a>0
所以a(b2+c2)≥2abc.
又因为c2+b2 ≥2bc,b>0
所以b(c2+a2)≥ 2abc.
因此a(b2+c2)+b(c2+a2)≥4abc.
证明:
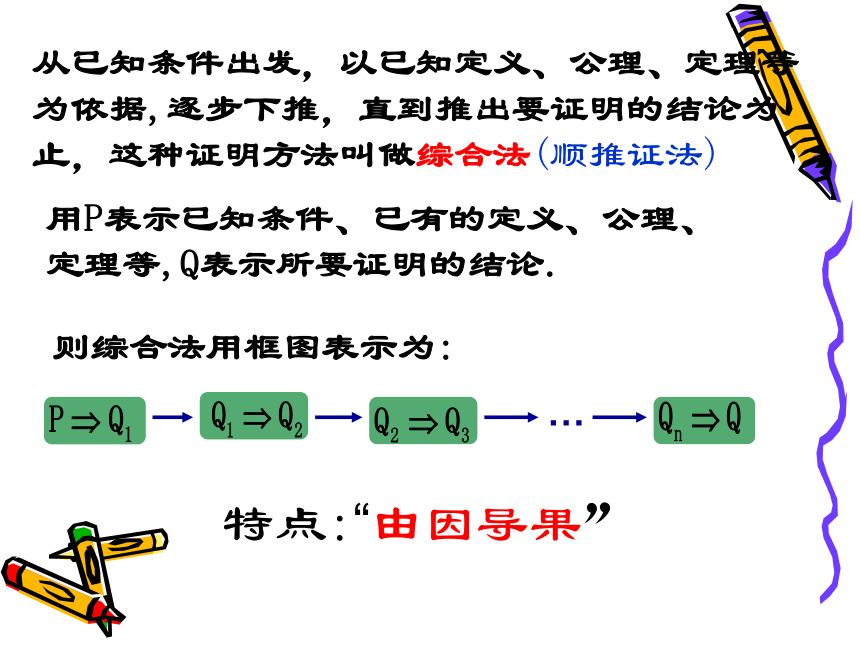
从已知条件出发,以已知定义、公理、定理等为依据,逐步下推,直到推出要证明的结论为止,这种证明方法叫做综合法(顺推证法)
用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.
则综合法用框图表示为:
…
特点:“由因导果”
例2:在△ABC中,三个内角A、B、C对应的边分别为a、b、c,且A、B、C成等差数列,a、b、c成等比数列,求证:△ABC为等边三角形.
符号语言
图形语言
文字语言
学会语言转换
找出隐含条件
练习:在锐角三角形ABC中,
求证:sinA+sinB+sinC>cosA+cosB+cosC
例3
【思路点拨】 解答本题可由已知条件出发,结合基本不等式,即可得出结论.
方法感悟
综合法证明问题的步骤
第一步:分析条件,选择方向.仔细分析题目的已知条件(包括隐含条件),分析已知与结论之间的联系与区别,选择相关的公理、定理、公式、结论,确定恰当的解题方法.
第二步:转化条件,组织过程.把题目的已知条件转化成解题所需要的语言,主要是文字、符号、图形三种语言之间的转化.组织过程时要有清晰的思路,严密的逻辑,简洁的语言.
第三步:适当调整,回顾反思.解题后回顾解题过程,可对部分步骤进行调整,有些语言可做适当的修饰,反思总结解题方法的选取.
小结:
综合法的定义和特点
布置作业
2.2直接证明与间接证明
2.2.1 综合法
熊德忠
12.5.19
两种推理的作用
1.推 理
合情推理
(或然性推理)
演绎推理
(必然性推理)
归纳
(特殊到一般)
类比
(特殊到特殊)
三段论
(一般到特殊)
复习
猜想需要推理
否定猜想
肯定猜想
举反例
证明
合情推理为演绎推理确定了目标和方向
演绎推理为合情推理提供了前提且对猜想作出判决和证明
温故夯基
归纳
类比
大前提
小前提
结论.
充分不必要
1
2
引例:四边形ABCD是平行四边形,
求证:AB=CD,BC=DA
A
B
C
D
1
3
4
2
证 连结AC,因为四边形ABCD是平行四边形
所以AB//CD,BC//DA
又AC=CA
故 AB=CD,BC=DA
直接从原命题的条件逐步推得命题成立的证明方法称为直接证明,其一般形式为:
本题条件
已知定义
已知定理
已知公理
本题结论
…
学习目标
1.了解直接证明的两种基本方法——综合法和分析法.
2.理解综合法和分析法的思考过程、特点,会用综合法和分析法证明数学问题.
例1:已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc
因为b2+c2 ≥2bc,a>0
所以a(b2+c2)≥2abc.
又因为c2+b2 ≥2bc,b>0
所以b(c2+a2)≥ 2abc.
因此a(b2+c2)+b(c2+a2)≥4abc.
证明:
从已知条件出发,以已知定义、公理、定理等为依据,逐步下推,直到推出要证明的结论为止,这种证明方法叫做综合法(顺推证法)
用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.
则综合法用框图表示为:
…
特点:“由因导果”
例2:在△ABC中,三个内角A、B、C对应的边分别为a、b、c,且A、B、C成等差数列,a、b、c成等比数列,求证:△ABC为等边三角形.
符号语言
图形语言
文字语言
学会语言转换
找出隐含条件
练习:在锐角三角形ABC中,
求证:sinA+sinB+sinC>cosA+cosB+cosC
例3
【思路点拨】 解答本题可由已知条件出发,结合基本不等式,即可得出结论.
方法感悟
综合法证明问题的步骤
第一步:分析条件,选择方向.仔细分析题目的已知条件(包括隐含条件),分析已知与结论之间的联系与区别,选择相关的公理、定理、公式、结论,确定恰当的解题方法.
第二步:转化条件,组织过程.把题目的已知条件转化成解题所需要的语言,主要是文字、符号、图形三种语言之间的转化.组织过程时要有清晰的思路,严密的逻辑,简洁的语言.
第三步:适当调整,回顾反思.解题后回顾解题过程,可对部分步骤进行调整,有些语言可做适当的修饰,反思总结解题方法的选取.
小结:
综合法的定义和特点
布置作业
