24.1.4 圆周角 同步练习(含答案)
文档属性
| 名称 | 24.1.4 圆周角 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-02 17:30:36 | ||
图片预览



文档简介
24.1 圆的有关性质
24.1.4 圆周角
一、选择题
1.下列图形中的角是圆周角的是 ( )
2.如图,已知点A,B,C在☉O上,∠A=72°,则∠OBC的度数是 ( )
A.12° B.15° C.18° D.20°
第2题图 第3题图 第4题图 第5题图
3.如图,△ABC的三个顶点都在☉O上,AB经过圆心O,∠A=60°,AC=2,则☉O的直径是 ( )
A.2 B.4 C.3 D.23
4.如图,四边形ABCD为☉O的内接四边形,∠BOD=120°,则∠BCD的大小是( )
A.120° B.100° C.80° D.60°
5.如图,△ABC内接于☉O,∠BAC=120°,AB=AC=6,BD为☉O的直径,则BD等于( )
A.4 B.6 C.8 D.12
6.(自贡中考)如图,☉O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )
A.15° B.25° C.30° D.75°
第6题图 第7题图 第9题图 第10题图
7.如图,在☉O中,弦AB⊥CD于点E.若已知AD=9,BC=12,则☉O的半径为( )
A.5.5 B.6 C.7.5 D.8
8.已知半径为5的☉O中,弦AB=52,弦AC=5,则∠BOC的度数是 ( )
A.15° B.210° C.30°或150° D.60°或90°
9.如图,A,B,C,D,E都是☉O上的点,AC=AE,∠B=118°,则∠D的度数为 ( )
A.122° B.124°
C.126° D.128°
10.如图,△ABC内接于☉O,∠A所对弧的度数为120°,∠ABC,∠ACB的平分线分别交AC,AB于点D,E,CE,BD相交于点F.以下四个结论:①∠BFE=60°;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的是( )
A.①④ B.①②③ C.①③ D.②③
11.(2020·十堰)如图,点A,B,C,D在⊙O上,OA⊥BC,垂足为E.若∠ADC=30°,AE=1,则BC=( )
A.2 B.4 C. D.2
第11题图 第12题图 第13题图 第14题图
12.(2020·杭州)如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )
A.3α+β=180° B.2α+β=180° C.3α-β=90° D.2α-β=90°
13.(中考·菏泽)如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是( )
A.64° B.58° C.32° D.26°
14.(中考·咸宁)如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A.6 B.8 C.5 D.5
15.(中考·陇南)如图,⊙A过点O(0,0),C(,0), D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是( )
A.15° B.30° C.45° D.60°
第15题图 第16题图 第17题图
16.(2020·张家界)如图,四边形ABCD为⊙O的内接四边形,已知∠BCD为120°,则∠BOD的度数为( )
A.100° B.110° C.120° D.130°
17.如图,已知⊙O为四边形ABCD的外接圆,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
A. B. C. D.
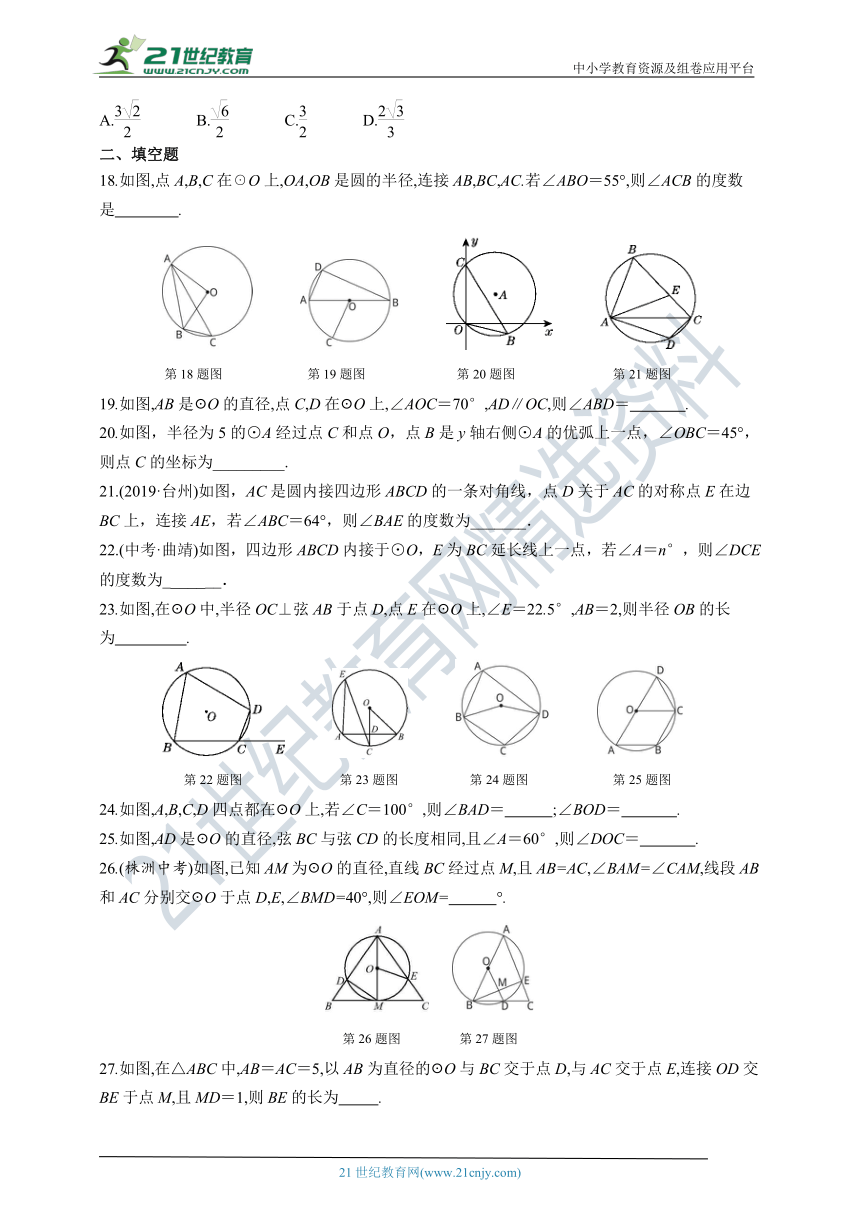
二、填空题
18.如图,点A,B,C在☉O上,OA,OB是圆的半径,连接AB,BC,AC.若∠ABO=55°,则∠ACB的度数是 .?
第18题图 第19题图 第20题图 第21题图
19.如图,AB是☉O的直径,点C,D在☉O上,∠AOC=70°,AD∥OC,则∠ABD= .?
20.如图,半径为5的⊙A经过点C和点O,点B是y轴右侧⊙A的优弧上一点,∠OBC=45°,则点C的坐标为_________.
21.(2019·台州)如图,AC是圆内接四边形ABCD的一条对角线,点D关于AC的对称点E在边BC上,连接AE,若∠ABC=64°,则∠BAE的度数为_______.
22.(中考·曲靖)如图,四边形ABCD内接于⊙O,E为BC延长线上一点,若∠A=n°,则∠DCE的度数为_______.
23.如图,在☉O中,半径OC⊥弦AB于点D,点E在☉O上,∠E=22.5°,AB=2,则半径OB的长为 .?
第22题图 第23题图 第24题图 第25题图
24.如图,A,B,C,D四点都在☉O上,若∠C=100°,则∠BAD= ;∠BOD= .?
25.如图,AD是☉O的直径,弦BC与弦CD的长度相同,且∠A=60°,则∠DOC= .?
26.(株洲中考)如图,已知AM为☉O的直径,直线BC经过点M,且AB=AC,∠BAM=∠CAM,线段AB和AC分别交☉O于点D,E,∠BMD=40°,则∠EOM= °.?
第26题图 第27题图
27.如图,在△ABC中,AB=AC=5,以AB为直径的☉O与BC交于点D,与AC交于点E,连接OD交BE于点M,且MD=1,则BE的长为 .?
三、解答题
28.如图,AB是☉O的直径,弦CD⊥AB于点E,∠ACD=30°,AE=2,求BD的长.
29.如图,四边形ABCD内接于☉O,AC,BD为其对角线,∠ACB=∠BAD,过点A作AE∥BC,交CD的延长线于点E.求证:EC=AC.
30.如图,AD是☉O的直径,点O是圆心,C,F是AD上的两点,OC=OF,B,E是☉O上的两点,且AB=DE.求证:BC∥EF.
31.如图,在☉O中,AB=CD,∠A=∠C,AB,CD交于点P.求证DP=BP.
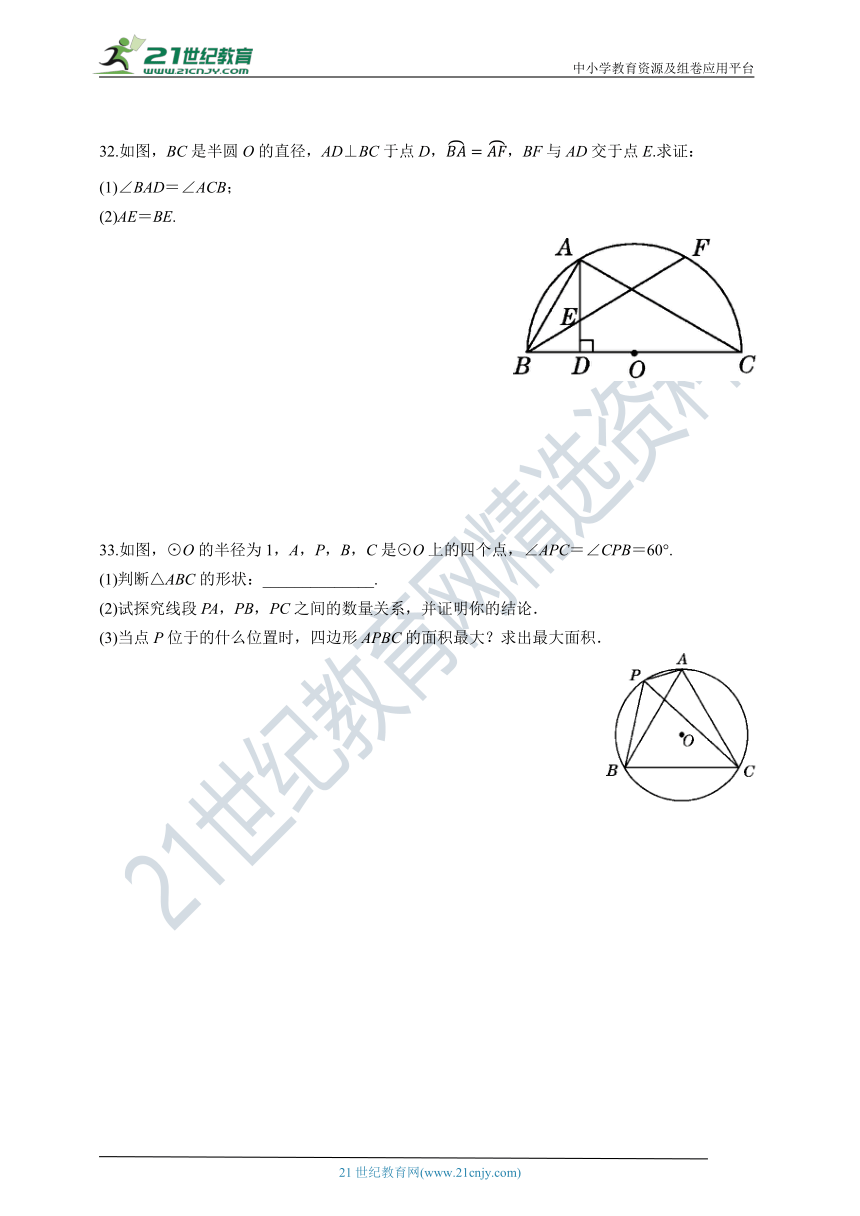
32.如图,BC是半圆O的直径,AD⊥BC于点D,BA=AF,BF与AD交于点E.求证:
(1)∠BAD=∠ACB;
(2)AE=BE.
33.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC的形状:______________.
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论.
(3)当点P位于的什么位置时,四边形APBC的面积最大?求出最大面积.
34.(中考·株洲)如图,已知AB是半径为1的⊙O的直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于点E,交AB于点F,且△AEF为等边三角形.
(1)求证:△DFB是等腰三角形;
(2)若DA=AF,求证:CF⊥AB.
35.如图,☉O的直径AB为10 cm,弦AC为6 cm,且AD=BD.
(1)求BC,AD,BD的长.
(2)图中还有一条线段CD的长是否能确定?若能,求出CD的长.
36.如图,在锐角△ABC中,AB>AC,AD⊥BC于点D,以AD为直径的☉O分别交AB,AC于点E,F,连接DE,DF.
(1)求证:∠EAF+∠EDF=180°.
(2)已知P是射线DC上的一个动点,当点P运动到PD=BD时,连接AP,交☉O于点G,连接DG.设∠EDG=∠α,∠APB=∠β,那么∠α与∠β有何数量关系?试证明你的结论.
37.[雅安中考改编]如图,四边形ABCD内接于圆,∠ABC=60°,对角线BD平分∠ADC.
(1)求证:△ABC是等边三角形;
(2)若AD=2,CD=3,求四边形ABCD的面积.
参考答案
一、选择题
1.下列图形中的角是圆周角的是 (B)
2.如图,已知点A,B,C在☉O上,∠A=72°,则∠OBC的度数是 (C)
A.12° B.15° C.18° D.20°
第2题图 第3题图 第4题图 第5题图
3.如图,△ABC的三个顶点都在☉O上,AB经过圆心O,∠A=60°,AC=2,则☉O的直径是 (B)
A.2 B.4 C.3 D.23
4.如图,四边形ABCD为☉O的内接四边形,∠BOD=120°,则∠BCD的大小是(A)
A.120° B.100° C.80° D.60°
5.如图,△ABC内接于☉O,∠BAC=120°,AB=AC=6,BD为☉O的直径,则BD等于( D )
A.4 B.6 C.8 D.12
6.(自贡中考)如图,☉O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( C )
A.15° B.25° C.30° D.75°
第6题图 第7题图 第9题图 第10题图
7.如图,在☉O中,弦AB⊥CD于点E.若已知AD=9,BC=12,则☉O的半径为( C )
A.5.5 B.6 C.7.5 D.8
8.已知半径为5的☉O中,弦AB=52,弦AC=5,则∠BOC的度数是 (C)
A.15° B.210° C.30°或150° D.60°或90°
9.如图,A,B,C,D,E都是☉O上的点,AC=AE,∠B=118°,则∠D的度数为 (B)
A.122° B.124°
C.126° D.128°
10.如图,△ABC内接于☉O,∠A所对弧的度数为120°,∠ABC,∠ACB的平分线分别交AC,AB于点D,E,CE,BD相交于点F.以下四个结论:①∠BFE=60°;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的是( C )
A.①④ B.①②③ C.①③ D.②③
11.(2020·十堰)如图,点A,B,C,D在⊙O上,OA⊥BC,垂足为E.若∠ADC=30°,AE=1,则BC=( )
A.2 B.4 C. D.2
第11题图 第12题图 第13题图 第14题图
【点拨】如图,连接OC.
∵∠ADC=30°,∴∠AOC=60°.
∵OA⊥BC,∴CE=BE.
在Rt△COE中,OE=OC,CE=OE.
∵OE=OA-AE=OC-1,
∴OC-1=OC,解得OC=2.
∴OE=1.
∴CE=.
∴BC=2CE=2.
【点拨】D
12.(2020·杭州)如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )
A.3α+β=180° B.2α+β=180° C.3α-β=90° D.2α-β=90°
【点拨】∵OA⊥BC,
∴∠AOB=∠AOC=90°.
∴∠DBC=90°-∠BEO=90°-∠AED=90°-α.
∴∠COD=2∠DBC=180°-2α.
∵∠AOD+∠COD=90°,
∴β+180°-2α=90°.
∴2α-β=90°.
【答案】D
13.(中考·菏泽)如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是( D )
A.64° B.58° C.32° D.26°
14.(中考·咸宁)如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A.6 B.8 C.5 D.5
【点拨】延长AO交⊙O于点E,连接BE,则∠AOB+∠BOE=180°.
∵∠AOB+∠COD=180°,
∴∠BOE=∠COD.
∴BE=CD=6.
∵AE为⊙O的直径,
∴∠ABE=90°.
∴AB===8.
【答案】B
15.(中考·陇南)如图,⊙A过点O(0,0),C(,0), D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是( )
A.15° B.30° C.45° D.60°
第15题图 第16题图 第17题图
【点拨】连接CD,由∠COD=90°,
可得CD是⊙A的直径.
容易求得CD=2,由OD=CD知∠OCD=30°,故∠OBD=∠OCD=30°.
【答案】B
16.(2020·张家界)如图,四边形ABCD为⊙O的内接四边形,已知∠BCD为120°,则∠BOD的度数为( C )
A.100° B.110° C.120° D.130°
17.如图,已知⊙O为四边形ABCD的外接圆,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
A. B. C. D.
【点拨】如图,作OE⊥AD于点E,连接BD,OD.
∵⊙O为四边形ABCD的外接圆,∠BCD=120°,
∴∠BAD=60°.
又∵AD=AB=2,∴△ABD是等边三角形.
易得DE=AD=1,∠ODE=∠ADB=30°,∴OE=OD.
在Rt△OED中,根据勾股定理可得OE2+DE2=OD2,得OD=.
【答案】D
二、填空题
18.如图,点A,B,C在☉O上,OA,OB是圆的半径,连接AB,BC,AC.若∠ABO=55°,则∠ACB的度数是 35° .?
第18题图 第19题图 第20题图 第21题图
19.如图,AB是☉O的直径,点C,D在☉O上,∠AOC=70°,AD∥OC,则∠ABD= 20° .?
20.如图,半径为5的⊙A经过点C和点O,点B是y轴右侧⊙A的优弧上一点,∠OBC=45°,则点C的坐标为___(0,5)_______.
21.(2019·台州)如图,AC是圆内接四边形ABCD的一条对角线,点D关于AC的对称点E在边BC上,连接AE,若∠ABC=64°,则∠BAE的度数为__52°______.
22.(中考·曲靖)如图,四边形ABCD内接于⊙O,E为BC延长线上一点,若∠A=n°,则∠DCE的度数为___n_____°
23.如图,在☉O中,半径OC⊥弦AB于点D,点E在☉O上,∠E=22.5°,AB=2,则半径OB的长为?2 .?
第22题图 第23题图 第24题图 第25题图
24.如图,A,B,C,D四点都在☉O上,若∠C=100°,则∠BAD= 80° ;∠BOD= 160° .?
25.如图,AD是☉O的直径,弦BC与弦CD的长度相同,且∠A=60°,则∠DOC= 60° .?
26.(株洲中考)如图,已知AM为☉O的直径,直线BC经过点M,且AB=AC,∠BAM=∠CAM,线段AB和AC分别交☉O于点D,E,∠BMD=40°,则∠EOM= 80 °.?
第26题图 第27题图
27.如图,在△ABC中,AB=AC=5,以AB为直径的☉O与BC交于点D,与AC交于点E,连接OD交BE于点M,且MD=1,则BE的长为 4 .?
三、解答题
28.如图,AB是☉O的直径,弦CD⊥AB于点E,∠ACD=30°,AE=2,求BD的长.
解:∵AB是☉O的直径,弦CD⊥AB,
∴CE=DE,∠AEC=∠DEB=90°.
∵∠B=∠ACD=30°,
∴在Rt△ACE中,AC=2AE=4,
CE=AC2-AE2=23,∴DE=CE=23.
在Rt△BDE中,∠B=30°,∴BD=2DE=43.
29.如图,四边形ABCD内接于☉O,AC,BD为其对角线,∠ACB=∠BAD,过点A作AE∥BC,交CD的延长线于点E.求证:EC=AC.
证明:∵AE∥BC,
∴∠E+∠BCE=180°,∠ACB=∠CAE.
由圆内接四边形的性质可知∠BAD+∠BCE=180°,
∴∠E=∠BAD.
∵∠ACB=∠BAD,∴∠E=∠CAE,
∴EC=AC.
30.如图,AD是☉O的直径,点O是圆心,C,F是AD上的两点,OC=OF,B,E是☉O上的两点,且AB=DE.求证:BC∥EF.
证明:∵AB=DE,AD是直径,
∴AB=DE,BD=AE,∴∠A=∠D.
∵OC=OF,OA=OD,∴AC=DF,
∴△BAC≌△EDF(SAS),∴∠ACB=∠DFE,
∴∠BCF=∠EFC,∴BC∥EF.
31.如图,在☉O中,AB=CD,∠A=∠C,AB,CD交于点P.求证DP=BP.
证明:∵AB=CD,∴CB=AD,∴AD=CB.
在△ADP和△CBP中,∠APD=∠CPB,∠A=∠C,AD=CB,
∴△ADP≌△CBP(AAS),∴DP=BP.
32.如图,BC是半圆O的直径,AD⊥BC于点D,BA=AF,BF与AD交于点E.求证:
(1)∠BAD=∠ACB;
证明:(1)∵BC是半圆O的直径,
∴∠BAC=90°.
∴∠BAD+∠CAD=90°.
又∵AD⊥BC,
∴∠ACB+∠CAD=90°.
∴∠BAD=∠ACB.
(2)AE=BE.
证明:∵BA=AF,
∴∠ACB=∠ABF.
由(1)知∠BAD=∠ACB,
∴∠ABF=∠BAD.
∴AE=BE.
33.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC的形状:_等边三角形_____________.
【思路点拨】由圆周角定理的推论判断△ABC的形状。
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论.
【思路点拨】在PC上截取PD=PA,连接AD,通过判断
△PAD的形状得出PA,PB,PC之间的数量关系。
解:PA+PB=PC.证明如下:
如图①,在PC上截取PD=PA,连接AD.
∵∠APC=60°,
∴△PAD是等边三角形.
∴PA=DA,∠PAD=60°.
∵∠CPB=60°,∴∠BAC=60°.
∴∠PAD=∠BAC.
∴∠PAB=∠DAC.
又∵AB=AC,
∴△PAB≌△DAC(SAS).
∴PB=DC.
∵PD+DC=PC,∴PA+PB=PC.
(3)当点P位于的什么位置时,四边形APBC的面积最大?求出最大面积.
【思路点拨】求BF的长,可以连接OC交BD于点H,根据垂径定理的推论和三角形的中位线定理可得OH=1,证明△COE≌△BOH,并利用勾股定理可得结论.
解:如图②,过点P作PE⊥AB,垂足为E;过点C作
CF⊥AB,垂足为F.
由(1)知△ABC是等边三角形,
∴F为AB的中点,且CF过圆心O.
∵S△PAB=AB·PE,
S△ABC=AB·CF,
∴S四边形APBC=AB·(PE+CF).
当点P为的中点时,E与F重合,PE+CF=PC,即PC为⊙O的直径.
∴此时四边形APBC的面积最大.
易求得AB=,
∴S四边形APBC=××2=.
34.(中考·株洲)如图,已知AB是半径为1的⊙O的直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于点E,交AB于点F,且△AEF为等边三角形.
(1)求证:△DFB是等腰三角形;
【思路点拨】由AB是⊙O的直径,得到∠ACB=90°,由△AEF为等边三角形,得到∠CAB=∠EFA=60°,根据三角形外角的性质即可得到结论。
证明:∵AB是⊙O的直径,
∴∠ACB=90°.
∵△AEF为等边三角形,
∴∠CAB=∠EFA=60°.
∴∠B=30°.
∵∠EFA=∠B+∠FDB,
∴∠B=∠FDB=30°.
∴FB=FD,即△DFB是等腰三角形.
(2)若DA=AF,求证:CF⊥AB.
【思路点拨】过点A作AM⊥DF于点M,设AF=2a,根据等边三角形的性质得到FM=EM=a,AM=a,再根据已知条件得到AB=AF+BF=8a,根据直角三角形的性质得到EF=CE=2a,推出∠ECF=∠EFC,根据三角形外角的性质可得到∠EFC=30°,从而可得到结论。
证明:过点A作AM⊥DF于点M,设AF=2a.
∵△AEF是等边三角形,
∴FM=EM=a,AM=a,
AE=EF=AF=2a.
在Rt△DAM中,DA=AF=2a,AM=a,
∴DM=5a.
∴DF=BF=6a.
∴AB=AF+BF=8a.
在Rt△ABC中,∠B=30°,∠ACB=90°,∴AC=4a.
∴CE=AC-AE=2a.∴CE=EF.
∴∠ECF=∠EFC.
∵∠AEF=∠ECF+∠EFC=60°,
∴∠EFC=30°.
∴∠AFC=∠EFA+∠EFC=60°+30°=90°,即CF⊥AB.
35.如图,☉O的直径AB为10 cm,弦AC为6 cm,且AD=BD.
(1)求BC,AD,BD的长.
(2)图中还有一条线段CD的长是否能确定?若能,求出CD的长.
解:(1)∵AB是☉O的直径,
∴∠ACB=∠ADB=90°.
∵AB=10 cm,AC=6 cm,∴BC=8 cm.
∵AD=BD,∴AD=BD=22AB=52 cm.
(2)图中线段CD的长能确定.作AE⊥CD于点E.
∵AE⊥CD,∠ACE=∠ABD=45°,
∴AE=CE=22AC=32 cm.
在Rt△AED中,DE=AD2-AE2=42 cm,
∴CD=CE+DE=32+42=72(cm).
36.如图,在锐角△ABC中,AB>AC,AD⊥BC于点D,以AD为直径的☉O分别交AB,AC于点E,F,连接DE,DF.
(1)求证:∠EAF+∠EDF=180°.
(2)已知P是射线DC上的一个动点,当点P运动到PD=BD时,连接AP,交☉O于点G,连接DG.设∠EDG=∠α,∠APB=∠β,那么∠α与∠β有何数量关系?试证明你的结论.
解:(1)在圆内接四边形AEDF中,AD为直径,
∴∠AED=∠AFD=90°.
又∵∠AED+∠AFD+∠EAF+∠EDF=360°,
∴∠EAF+∠EDF=360°-(∠AED+∠AFD)=180°.
(2)∠α=2∠β.
理由:如图,
在△ABD与△APD中,AD⊥BP,且BD=DP,AD=AD,∴△ABD≌△APD(SAS),∴∠B=∠APD=∠β.
在△ABP中,∠EAG+∠B+∠APD=180°,
∴∠EAG+2∠β=180°.
由(1)知∠EAG+∠EDG=180°,∴∠EAG+∠α=180°,∴∠α=2∠β.
37.[雅安中考改编]如图,四边形ABCD内接于圆,∠ABC=60°,对角线BD平分∠ADC.
(1)求证:△ABC是等边三角形;
(2)若AD=2,CD=3,求四边形ABCD的面积.
解:(1)由圆内接四边形的性质可知∠ABC+∠ADC=180°.
∵∠ABC=60°,∴∠ADC=120°.
∵BD平分∠ADC,∴∠ADB=∠CDB=60°,
∴∠ACB=∠ADB=60°,∠BAC=∠CDB=60°,
∴∠ABC=∠ACB=∠BAC,
∴△ABC是等边三角形.
(2)过点A作AM⊥CD交CD延长线于点M,过点B作BN⊥AC,垂足为N,∴∠AMD=90°.
∵∠ADC=120°,∴∠ADM=60°,∴∠DAM=30°,
∴DM=12AD=1,AM=AD2-DM2=3.
∵CD=3,∴CM=CD+DM=4,
∴S△ACD=12CD·AM=332,
在Rt△AMC中,AC=AM2+CM2=19.
∵△ABC是等边三角形,∴AB=BC=AC=19,
∴BN=32BC=572,
∴S△ABC=12AC·BN=1934,
∴S四边形ABCD=S△ACD+S△ABC=2534.
24.1.4 圆周角
一、选择题
1.下列图形中的角是圆周角的是 ( )
2.如图,已知点A,B,C在☉O上,∠A=72°,则∠OBC的度数是 ( )
A.12° B.15° C.18° D.20°
第2题图 第3题图 第4题图 第5题图
3.如图,△ABC的三个顶点都在☉O上,AB经过圆心O,∠A=60°,AC=2,则☉O的直径是 ( )
A.2 B.4 C.3 D.23
4.如图,四边形ABCD为☉O的内接四边形,∠BOD=120°,则∠BCD的大小是( )
A.120° B.100° C.80° D.60°
5.如图,△ABC内接于☉O,∠BAC=120°,AB=AC=6,BD为☉O的直径,则BD等于( )
A.4 B.6 C.8 D.12
6.(自贡中考)如图,☉O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )
A.15° B.25° C.30° D.75°
第6题图 第7题图 第9题图 第10题图
7.如图,在☉O中,弦AB⊥CD于点E.若已知AD=9,BC=12,则☉O的半径为( )
A.5.5 B.6 C.7.5 D.8
8.已知半径为5的☉O中,弦AB=52,弦AC=5,则∠BOC的度数是 ( )
A.15° B.210° C.30°或150° D.60°或90°
9.如图,A,B,C,D,E都是☉O上的点,AC=AE,∠B=118°,则∠D的度数为 ( )
A.122° B.124°
C.126° D.128°
10.如图,△ABC内接于☉O,∠A所对弧的度数为120°,∠ABC,∠ACB的平分线分别交AC,AB于点D,E,CE,BD相交于点F.以下四个结论:①∠BFE=60°;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的是( )
A.①④ B.①②③ C.①③ D.②③
11.(2020·十堰)如图,点A,B,C,D在⊙O上,OA⊥BC,垂足为E.若∠ADC=30°,AE=1,则BC=( )
A.2 B.4 C. D.2
第11题图 第12题图 第13题图 第14题图
12.(2020·杭州)如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )
A.3α+β=180° B.2α+β=180° C.3α-β=90° D.2α-β=90°
13.(中考·菏泽)如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是( )
A.64° B.58° C.32° D.26°
14.(中考·咸宁)如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A.6 B.8 C.5 D.5
15.(中考·陇南)如图,⊙A过点O(0,0),C(,0), D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是( )
A.15° B.30° C.45° D.60°
第15题图 第16题图 第17题图
16.(2020·张家界)如图,四边形ABCD为⊙O的内接四边形,已知∠BCD为120°,则∠BOD的度数为( )
A.100° B.110° C.120° D.130°
17.如图,已知⊙O为四边形ABCD的外接圆,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
A. B. C. D.
二、填空题
18.如图,点A,B,C在☉O上,OA,OB是圆的半径,连接AB,BC,AC.若∠ABO=55°,则∠ACB的度数是 .?
第18题图 第19题图 第20题图 第21题图
19.如图,AB是☉O的直径,点C,D在☉O上,∠AOC=70°,AD∥OC,则∠ABD= .?
20.如图,半径为5的⊙A经过点C和点O,点B是y轴右侧⊙A的优弧上一点,∠OBC=45°,则点C的坐标为_________.
21.(2019·台州)如图,AC是圆内接四边形ABCD的一条对角线,点D关于AC的对称点E在边BC上,连接AE,若∠ABC=64°,则∠BAE的度数为_______.
22.(中考·曲靖)如图,四边形ABCD内接于⊙O,E为BC延长线上一点,若∠A=n°,则∠DCE的度数为_______.
23.如图,在☉O中,半径OC⊥弦AB于点D,点E在☉O上,∠E=22.5°,AB=2,则半径OB的长为 .?
第22题图 第23题图 第24题图 第25题图
24.如图,A,B,C,D四点都在☉O上,若∠C=100°,则∠BAD= ;∠BOD= .?
25.如图,AD是☉O的直径,弦BC与弦CD的长度相同,且∠A=60°,则∠DOC= .?
26.(株洲中考)如图,已知AM为☉O的直径,直线BC经过点M,且AB=AC,∠BAM=∠CAM,线段AB和AC分别交☉O于点D,E,∠BMD=40°,则∠EOM= °.?
第26题图 第27题图
27.如图,在△ABC中,AB=AC=5,以AB为直径的☉O与BC交于点D,与AC交于点E,连接OD交BE于点M,且MD=1,则BE的长为 .?
三、解答题
28.如图,AB是☉O的直径,弦CD⊥AB于点E,∠ACD=30°,AE=2,求BD的长.
29.如图,四边形ABCD内接于☉O,AC,BD为其对角线,∠ACB=∠BAD,过点A作AE∥BC,交CD的延长线于点E.求证:EC=AC.
30.如图,AD是☉O的直径,点O是圆心,C,F是AD上的两点,OC=OF,B,E是☉O上的两点,且AB=DE.求证:BC∥EF.
31.如图,在☉O中,AB=CD,∠A=∠C,AB,CD交于点P.求证DP=BP.
32.如图,BC是半圆O的直径,AD⊥BC于点D,BA=AF,BF与AD交于点E.求证:
(1)∠BAD=∠ACB;
(2)AE=BE.
33.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC的形状:______________.
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论.
(3)当点P位于的什么位置时,四边形APBC的面积最大?求出最大面积.
34.(中考·株洲)如图,已知AB是半径为1的⊙O的直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于点E,交AB于点F,且△AEF为等边三角形.
(1)求证:△DFB是等腰三角形;
(2)若DA=AF,求证:CF⊥AB.
35.如图,☉O的直径AB为10 cm,弦AC为6 cm,且AD=BD.
(1)求BC,AD,BD的长.
(2)图中还有一条线段CD的长是否能确定?若能,求出CD的长.
36.如图,在锐角△ABC中,AB>AC,AD⊥BC于点D,以AD为直径的☉O分别交AB,AC于点E,F,连接DE,DF.
(1)求证:∠EAF+∠EDF=180°.
(2)已知P是射线DC上的一个动点,当点P运动到PD=BD时,连接AP,交☉O于点G,连接DG.设∠EDG=∠α,∠APB=∠β,那么∠α与∠β有何数量关系?试证明你的结论.
37.[雅安中考改编]如图,四边形ABCD内接于圆,∠ABC=60°,对角线BD平分∠ADC.
(1)求证:△ABC是等边三角形;
(2)若AD=2,CD=3,求四边形ABCD的面积.
参考答案
一、选择题
1.下列图形中的角是圆周角的是 (B)
2.如图,已知点A,B,C在☉O上,∠A=72°,则∠OBC的度数是 (C)
A.12° B.15° C.18° D.20°
第2题图 第3题图 第4题图 第5题图
3.如图,△ABC的三个顶点都在☉O上,AB经过圆心O,∠A=60°,AC=2,则☉O的直径是 (B)
A.2 B.4 C.3 D.23
4.如图,四边形ABCD为☉O的内接四边形,∠BOD=120°,则∠BCD的大小是(A)
A.120° B.100° C.80° D.60°
5.如图,△ABC内接于☉O,∠BAC=120°,AB=AC=6,BD为☉O的直径,则BD等于( D )
A.4 B.6 C.8 D.12
6.(自贡中考)如图,☉O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( C )
A.15° B.25° C.30° D.75°
第6题图 第7题图 第9题图 第10题图
7.如图,在☉O中,弦AB⊥CD于点E.若已知AD=9,BC=12,则☉O的半径为( C )
A.5.5 B.6 C.7.5 D.8
8.已知半径为5的☉O中,弦AB=52,弦AC=5,则∠BOC的度数是 (C)
A.15° B.210° C.30°或150° D.60°或90°
9.如图,A,B,C,D,E都是☉O上的点,AC=AE,∠B=118°,则∠D的度数为 (B)
A.122° B.124°
C.126° D.128°
10.如图,△ABC内接于☉O,∠A所对弧的度数为120°,∠ABC,∠ACB的平分线分别交AC,AB于点D,E,CE,BD相交于点F.以下四个结论:①∠BFE=60°;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的是( C )
A.①④ B.①②③ C.①③ D.②③
11.(2020·十堰)如图,点A,B,C,D在⊙O上,OA⊥BC,垂足为E.若∠ADC=30°,AE=1,则BC=( )
A.2 B.4 C. D.2
第11题图 第12题图 第13题图 第14题图
【点拨】如图,连接OC.
∵∠ADC=30°,∴∠AOC=60°.
∵OA⊥BC,∴CE=BE.
在Rt△COE中,OE=OC,CE=OE.
∵OE=OA-AE=OC-1,
∴OC-1=OC,解得OC=2.
∴OE=1.
∴CE=.
∴BC=2CE=2.
【点拨】D
12.(2020·杭州)如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )
A.3α+β=180° B.2α+β=180° C.3α-β=90° D.2α-β=90°
【点拨】∵OA⊥BC,
∴∠AOB=∠AOC=90°.
∴∠DBC=90°-∠BEO=90°-∠AED=90°-α.
∴∠COD=2∠DBC=180°-2α.
∵∠AOD+∠COD=90°,
∴β+180°-2α=90°.
∴2α-β=90°.
【答案】D
13.(中考·菏泽)如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是( D )
A.64° B.58° C.32° D.26°
14.(中考·咸宁)如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A.6 B.8 C.5 D.5
【点拨】延长AO交⊙O于点E,连接BE,则∠AOB+∠BOE=180°.
∵∠AOB+∠COD=180°,
∴∠BOE=∠COD.
∴BE=CD=6.
∵AE为⊙O的直径,
∴∠ABE=90°.
∴AB===8.
【答案】B
15.(中考·陇南)如图,⊙A过点O(0,0),C(,0), D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是( )
A.15° B.30° C.45° D.60°
第15题图 第16题图 第17题图
【点拨】连接CD,由∠COD=90°,
可得CD是⊙A的直径.
容易求得CD=2,由OD=CD知∠OCD=30°,故∠OBD=∠OCD=30°.
【答案】B
16.(2020·张家界)如图,四边形ABCD为⊙O的内接四边形,已知∠BCD为120°,则∠BOD的度数为( C )
A.100° B.110° C.120° D.130°
17.如图,已知⊙O为四边形ABCD的外接圆,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
A. B. C. D.
【点拨】如图,作OE⊥AD于点E,连接BD,OD.
∵⊙O为四边形ABCD的外接圆,∠BCD=120°,
∴∠BAD=60°.
又∵AD=AB=2,∴△ABD是等边三角形.
易得DE=AD=1,∠ODE=∠ADB=30°,∴OE=OD.
在Rt△OED中,根据勾股定理可得OE2+DE2=OD2,得OD=.
【答案】D
二、填空题
18.如图,点A,B,C在☉O上,OA,OB是圆的半径,连接AB,BC,AC.若∠ABO=55°,则∠ACB的度数是 35° .?
第18题图 第19题图 第20题图 第21题图
19.如图,AB是☉O的直径,点C,D在☉O上,∠AOC=70°,AD∥OC,则∠ABD= 20° .?
20.如图,半径为5的⊙A经过点C和点O,点B是y轴右侧⊙A的优弧上一点,∠OBC=45°,则点C的坐标为___(0,5)_______.
21.(2019·台州)如图,AC是圆内接四边形ABCD的一条对角线,点D关于AC的对称点E在边BC上,连接AE,若∠ABC=64°,则∠BAE的度数为__52°______.
22.(中考·曲靖)如图,四边形ABCD内接于⊙O,E为BC延长线上一点,若∠A=n°,则∠DCE的度数为___n_____°
23.如图,在☉O中,半径OC⊥弦AB于点D,点E在☉O上,∠E=22.5°,AB=2,则半径OB的长为?2 .?
第22题图 第23题图 第24题图 第25题图
24.如图,A,B,C,D四点都在☉O上,若∠C=100°,则∠BAD= 80° ;∠BOD= 160° .?
25.如图,AD是☉O的直径,弦BC与弦CD的长度相同,且∠A=60°,则∠DOC= 60° .?
26.(株洲中考)如图,已知AM为☉O的直径,直线BC经过点M,且AB=AC,∠BAM=∠CAM,线段AB和AC分别交☉O于点D,E,∠BMD=40°,则∠EOM= 80 °.?
第26题图 第27题图
27.如图,在△ABC中,AB=AC=5,以AB为直径的☉O与BC交于点D,与AC交于点E,连接OD交BE于点M,且MD=1,则BE的长为 4 .?
三、解答题
28.如图,AB是☉O的直径,弦CD⊥AB于点E,∠ACD=30°,AE=2,求BD的长.
解:∵AB是☉O的直径,弦CD⊥AB,
∴CE=DE,∠AEC=∠DEB=90°.
∵∠B=∠ACD=30°,
∴在Rt△ACE中,AC=2AE=4,
CE=AC2-AE2=23,∴DE=CE=23.
在Rt△BDE中,∠B=30°,∴BD=2DE=43.
29.如图,四边形ABCD内接于☉O,AC,BD为其对角线,∠ACB=∠BAD,过点A作AE∥BC,交CD的延长线于点E.求证:EC=AC.
证明:∵AE∥BC,
∴∠E+∠BCE=180°,∠ACB=∠CAE.
由圆内接四边形的性质可知∠BAD+∠BCE=180°,
∴∠E=∠BAD.
∵∠ACB=∠BAD,∴∠E=∠CAE,
∴EC=AC.
30.如图,AD是☉O的直径,点O是圆心,C,F是AD上的两点,OC=OF,B,E是☉O上的两点,且AB=DE.求证:BC∥EF.
证明:∵AB=DE,AD是直径,
∴AB=DE,BD=AE,∴∠A=∠D.
∵OC=OF,OA=OD,∴AC=DF,
∴△BAC≌△EDF(SAS),∴∠ACB=∠DFE,
∴∠BCF=∠EFC,∴BC∥EF.
31.如图,在☉O中,AB=CD,∠A=∠C,AB,CD交于点P.求证DP=BP.
证明:∵AB=CD,∴CB=AD,∴AD=CB.
在△ADP和△CBP中,∠APD=∠CPB,∠A=∠C,AD=CB,
∴△ADP≌△CBP(AAS),∴DP=BP.
32.如图,BC是半圆O的直径,AD⊥BC于点D,BA=AF,BF与AD交于点E.求证:
(1)∠BAD=∠ACB;
证明:(1)∵BC是半圆O的直径,
∴∠BAC=90°.
∴∠BAD+∠CAD=90°.
又∵AD⊥BC,
∴∠ACB+∠CAD=90°.
∴∠BAD=∠ACB.
(2)AE=BE.
证明:∵BA=AF,
∴∠ACB=∠ABF.
由(1)知∠BAD=∠ACB,
∴∠ABF=∠BAD.
∴AE=BE.
33.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC的形状:_等边三角形_____________.
【思路点拨】由圆周角定理的推论判断△ABC的形状。
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论.
【思路点拨】在PC上截取PD=PA,连接AD,通过判断
△PAD的形状得出PA,PB,PC之间的数量关系。
解:PA+PB=PC.证明如下:
如图①,在PC上截取PD=PA,连接AD.
∵∠APC=60°,
∴△PAD是等边三角形.
∴PA=DA,∠PAD=60°.
∵∠CPB=60°,∴∠BAC=60°.
∴∠PAD=∠BAC.
∴∠PAB=∠DAC.
又∵AB=AC,
∴△PAB≌△DAC(SAS).
∴PB=DC.
∵PD+DC=PC,∴PA+PB=PC.
(3)当点P位于的什么位置时,四边形APBC的面积最大?求出最大面积.
【思路点拨】求BF的长,可以连接OC交BD于点H,根据垂径定理的推论和三角形的中位线定理可得OH=1,证明△COE≌△BOH,并利用勾股定理可得结论.
解:如图②,过点P作PE⊥AB,垂足为E;过点C作
CF⊥AB,垂足为F.
由(1)知△ABC是等边三角形,
∴F为AB的中点,且CF过圆心O.
∵S△PAB=AB·PE,
S△ABC=AB·CF,
∴S四边形APBC=AB·(PE+CF).
当点P为的中点时,E与F重合,PE+CF=PC,即PC为⊙O的直径.
∴此时四边形APBC的面积最大.
易求得AB=,
∴S四边形APBC=××2=.
34.(中考·株洲)如图,已知AB是半径为1的⊙O的直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于点E,交AB于点F,且△AEF为等边三角形.
(1)求证:△DFB是等腰三角形;
【思路点拨】由AB是⊙O的直径,得到∠ACB=90°,由△AEF为等边三角形,得到∠CAB=∠EFA=60°,根据三角形外角的性质即可得到结论。
证明:∵AB是⊙O的直径,
∴∠ACB=90°.
∵△AEF为等边三角形,
∴∠CAB=∠EFA=60°.
∴∠B=30°.
∵∠EFA=∠B+∠FDB,
∴∠B=∠FDB=30°.
∴FB=FD,即△DFB是等腰三角形.
(2)若DA=AF,求证:CF⊥AB.
【思路点拨】过点A作AM⊥DF于点M,设AF=2a,根据等边三角形的性质得到FM=EM=a,AM=a,再根据已知条件得到AB=AF+BF=8a,根据直角三角形的性质得到EF=CE=2a,推出∠ECF=∠EFC,根据三角形外角的性质可得到∠EFC=30°,从而可得到结论。
证明:过点A作AM⊥DF于点M,设AF=2a.
∵△AEF是等边三角形,
∴FM=EM=a,AM=a,
AE=EF=AF=2a.
在Rt△DAM中,DA=AF=2a,AM=a,
∴DM=5a.
∴DF=BF=6a.
∴AB=AF+BF=8a.
在Rt△ABC中,∠B=30°,∠ACB=90°,∴AC=4a.
∴CE=AC-AE=2a.∴CE=EF.
∴∠ECF=∠EFC.
∵∠AEF=∠ECF+∠EFC=60°,
∴∠EFC=30°.
∴∠AFC=∠EFA+∠EFC=60°+30°=90°,即CF⊥AB.
35.如图,☉O的直径AB为10 cm,弦AC为6 cm,且AD=BD.
(1)求BC,AD,BD的长.
(2)图中还有一条线段CD的长是否能确定?若能,求出CD的长.
解:(1)∵AB是☉O的直径,
∴∠ACB=∠ADB=90°.
∵AB=10 cm,AC=6 cm,∴BC=8 cm.
∵AD=BD,∴AD=BD=22AB=52 cm.
(2)图中线段CD的长能确定.作AE⊥CD于点E.
∵AE⊥CD,∠ACE=∠ABD=45°,
∴AE=CE=22AC=32 cm.
在Rt△AED中,DE=AD2-AE2=42 cm,
∴CD=CE+DE=32+42=72(cm).
36.如图,在锐角△ABC中,AB>AC,AD⊥BC于点D,以AD为直径的☉O分别交AB,AC于点E,F,连接DE,DF.
(1)求证:∠EAF+∠EDF=180°.
(2)已知P是射线DC上的一个动点,当点P运动到PD=BD时,连接AP,交☉O于点G,连接DG.设∠EDG=∠α,∠APB=∠β,那么∠α与∠β有何数量关系?试证明你的结论.
解:(1)在圆内接四边形AEDF中,AD为直径,
∴∠AED=∠AFD=90°.
又∵∠AED+∠AFD+∠EAF+∠EDF=360°,
∴∠EAF+∠EDF=360°-(∠AED+∠AFD)=180°.
(2)∠α=2∠β.
理由:如图,
在△ABD与△APD中,AD⊥BP,且BD=DP,AD=AD,∴△ABD≌△APD(SAS),∴∠B=∠APD=∠β.
在△ABP中,∠EAG+∠B+∠APD=180°,
∴∠EAG+2∠β=180°.
由(1)知∠EAG+∠EDG=180°,∴∠EAG+∠α=180°,∴∠α=2∠β.
37.[雅安中考改编]如图,四边形ABCD内接于圆,∠ABC=60°,对角线BD平分∠ADC.
(1)求证:△ABC是等边三角形;
(2)若AD=2,CD=3,求四边形ABCD的面积.
解:(1)由圆内接四边形的性质可知∠ABC+∠ADC=180°.
∵∠ABC=60°,∴∠ADC=120°.
∵BD平分∠ADC,∴∠ADB=∠CDB=60°,
∴∠ACB=∠ADB=60°,∠BAC=∠CDB=60°,
∴∠ABC=∠ACB=∠BAC,
∴△ABC是等边三角形.
(2)过点A作AM⊥CD交CD延长线于点M,过点B作BN⊥AC,垂足为N,∴∠AMD=90°.
∵∠ADC=120°,∴∠ADM=60°,∴∠DAM=30°,
∴DM=12AD=1,AM=AD2-DM2=3.
∵CD=3,∴CM=CD+DM=4,
∴S△ACD=12CD·AM=332,
在Rt△AMC中,AC=AM2+CM2=19.
∵△ABC是等边三角形,∴AB=BC=AC=19,
∴BN=32BC=572,
∴S△ABC=12AC·BN=1934,
∴S四边形ABCD=S△ACD+S△ABC=2534.
同课章节目录
