5.6有理数的乘法(1)
图片预览

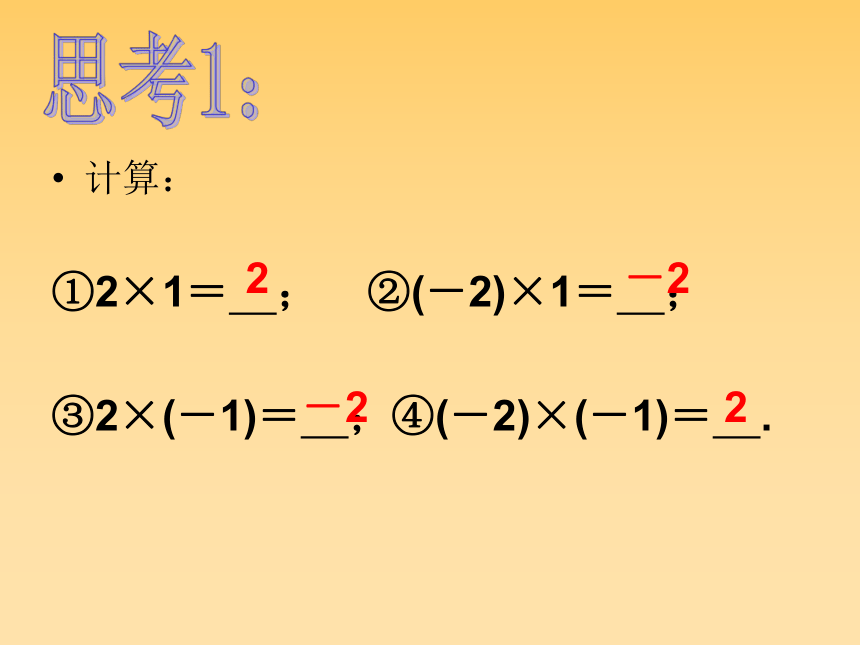




文档简介
(共18张PPT)
计算:
①2×1= ; ②(-2)×1= ;
③2×(-1)= ;④(-2)×(-1)= .
2
2
-2
-2
约定:向东每小时行80千米记作80千米,
向西每小时行80千米记作 – 80千米.
约定:2小时后记作2小时,2小时前记作 – 2小时.
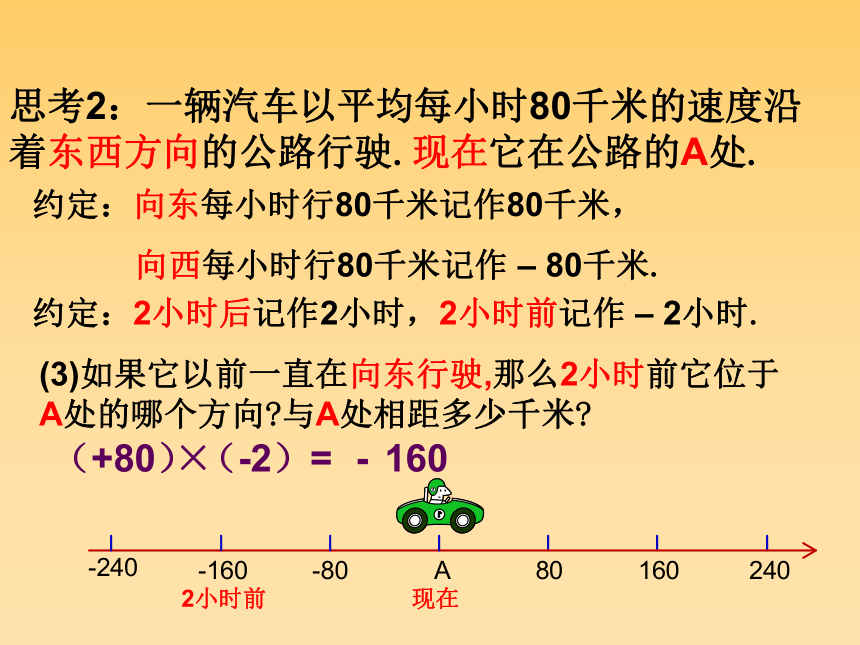
思考2:一辆汽车以平均每小时80千米的速度沿着东西方向的公路行驶.现在它在公路的A处.
现在
约定:向东每小时行80千米记作80千米,
向西每小时行80千米记作 – 80千米.
约定:2小时后记作2小时,2小时前记作 – 2小时.
思考2:一辆汽车以平均每小时80千米的速度沿着东西方向的公路行驶.现在它在公路的A处.
现在
(1)如果它向东行驶2小时,那么它位于A处的哪个方向 与A处相距多少千米
2小时后
=
(+80)
×
(+2)
160
+
约定:向东每小时行80千米记作80千米,
向西每小时行80千米记作 – 80千米.
约定:2小时后记作2小时,2小时前记作 – 2小时.
思考2:一辆汽车以平均每小时80千米的速度沿着东西方向的公路行驶.现在它在公路的A处.
现在
(2)如果它向西行驶2小时,那么它位于A处的哪个方向 与A处相距多少千米
2小时后
=
(-80)
×
(+2)
160
-
约定:向东每小时行80千米记作80千米,
向西每小时行80千米记作 – 80千米.
约定:2小时后记作2小时,2小时前记作 – 2小时.
思考2:一辆汽车以平均每小时80千米的速度沿着东西方向的公路行驶.现在它在公路的A处.
现在
(3)如果它以前一直在向东行驶,那么2小时前它位于A处的哪个方向 与A处相距多少千米
2小时前
=
(+80)
×
(-2)
160
-
约定:向东每小时行80千米记作80千米,
向西每小时行80千米记作 – 80千米.
约定:2小时后记作2小时,2小时前记作 – 2小时.
思考2:一辆汽车以平均每小时80千米的速度沿着东西方向的公路行驶.现在它在公路的A处.
现在
2小时前
(4)如果它以前一直在向西行驶,那么2小时前它位于A处的哪个方向 与A处相距多少千米
=
(-80)
×
(-2)
160
+
通过上例,我们得到4个式子:
(+80)×(+2) = +160
(- 80)×(+2) = - 160
(+80)×(- 2) = -160
(- 80)×(- 2) = +160
想一想:
积的符号与两因数的符号有什么关系?
正数
×
正数
正数
=
符号关系
负数
×
负数
正数
=
正数
×
负数
负数
=
负数
×
正数
负数
=
两数相乘,同号得正,异号得负
通过上例,我们得到4个式子:
(+80)×(+2) = +160
(- 80)×(+2) = - 160
(+80)×(- 2) = -160
(- 80)×(- 2) = +160
想一想:
积的绝对值与两因数的绝对值有什么关系?
80
×
160
2
=
绝对值关系
80
×
160
2
=
80
×
160
2
=
80
×
160
2
=
积的绝对值等于两因数的绝对值相乘
两数相乘,同号得正,异号得负,
并把绝对值相乘。
观察:
80×0=?
0×(- 80) =?
0 ×0=?
任何数与零相乘,都得零。
练一练:判断符号
6×(-9)
(-6)×(-9)
(-6)×9
(-6)×1
(-6)×(-1)
6×(-1)
(-4)×0.25
(-4)×(-0.25)
4×(-0.25)
口答:
6×(-9)
(-6)×(-9)
(-6)×9
(-6)×1
(-6)×(-1)
6×(-1)
(-6)×0
0×(-6)
(-4)×0.25
补充练习:
1.两数相乘的积为正,这两个数
______ (同号、异号)
两数相乘的积为负,这两个数
______ (同号、异号)
异号
同号
2.判断下列方程的解是正数还是负 数或0:
(1)4x=-16;
(2)-3x=18;
(3)-9x=-36;
(4)-5x=0.
1、两数相乘,同号得正,异号得负,
并把绝对值相乘。
2、任何数同0相乘,都得0。
3、有理数乘法运算顺序:
先确定积的符号,再确定积的绝对值
有理数的乘法,关键是确定积的符号,三个或三个以上的有理数相乘如何确定积的符号呢?
(-2)×3×4;
(-2)×(-3)×4;
(3) (-2)×(-3)×(-4)×5;
(4) (-2)×(-3)×(-4)×(-5);
(5) (-2)×(-3)×(-4)×(-5)×0.
作业布置:
1、练习册习题5.6/1、2、3题
2、一课一练5.7
计算:
①2×1= ; ②(-2)×1= ;
③2×(-1)= ;④(-2)×(-1)= .
2
2
-2
-2
约定:向东每小时行80千米记作80千米,
向西每小时行80千米记作 – 80千米.
约定:2小时后记作2小时,2小时前记作 – 2小时.
思考2:一辆汽车以平均每小时80千米的速度沿着东西方向的公路行驶.现在它在公路的A处.
现在
约定:向东每小时行80千米记作80千米,
向西每小时行80千米记作 – 80千米.
约定:2小时后记作2小时,2小时前记作 – 2小时.
思考2:一辆汽车以平均每小时80千米的速度沿着东西方向的公路行驶.现在它在公路的A处.
现在
(1)如果它向东行驶2小时,那么它位于A处的哪个方向 与A处相距多少千米
2小时后
=
(+80)
×
(+2)
160
+
约定:向东每小时行80千米记作80千米,
向西每小时行80千米记作 – 80千米.
约定:2小时后记作2小时,2小时前记作 – 2小时.
思考2:一辆汽车以平均每小时80千米的速度沿着东西方向的公路行驶.现在它在公路的A处.
现在
(2)如果它向西行驶2小时,那么它位于A处的哪个方向 与A处相距多少千米
2小时后
=
(-80)
×
(+2)
160
-
约定:向东每小时行80千米记作80千米,
向西每小时行80千米记作 – 80千米.
约定:2小时后记作2小时,2小时前记作 – 2小时.
思考2:一辆汽车以平均每小时80千米的速度沿着东西方向的公路行驶.现在它在公路的A处.
现在
(3)如果它以前一直在向东行驶,那么2小时前它位于A处的哪个方向 与A处相距多少千米
2小时前
=
(+80)
×
(-2)
160
-
约定:向东每小时行80千米记作80千米,
向西每小时行80千米记作 – 80千米.
约定:2小时后记作2小时,2小时前记作 – 2小时.
思考2:一辆汽车以平均每小时80千米的速度沿着东西方向的公路行驶.现在它在公路的A处.
现在
2小时前
(4)如果它以前一直在向西行驶,那么2小时前它位于A处的哪个方向 与A处相距多少千米
=
(-80)
×
(-2)
160
+
通过上例,我们得到4个式子:
(+80)×(+2) = +160
(- 80)×(+2) = - 160
(+80)×(- 2) = -160
(- 80)×(- 2) = +160
想一想:
积的符号与两因数的符号有什么关系?
正数
×
正数
正数
=
符号关系
负数
×
负数
正数
=
正数
×
负数
负数
=
负数
×
正数
负数
=
两数相乘,同号得正,异号得负
通过上例,我们得到4个式子:
(+80)×(+2) = +160
(- 80)×(+2) = - 160
(+80)×(- 2) = -160
(- 80)×(- 2) = +160
想一想:
积的绝对值与两因数的绝对值有什么关系?
80
×
160
2
=
绝对值关系
80
×
160
2
=
80
×
160
2
=
80
×
160
2
=
积的绝对值等于两因数的绝对值相乘
两数相乘,同号得正,异号得负,
并把绝对值相乘。
观察:
80×0=?
0×(- 80) =?
0 ×0=?
任何数与零相乘,都得零。
练一练:判断符号
6×(-9)
(-6)×(-9)
(-6)×9
(-6)×1
(-6)×(-1)
6×(-1)
(-4)×0.25
(-4)×(-0.25)
4×(-0.25)
口答:
6×(-9)
(-6)×(-9)
(-6)×9
(-6)×1
(-6)×(-1)
6×(-1)
(-6)×0
0×(-6)
(-4)×0.25
补充练习:
1.两数相乘的积为正,这两个数
______ (同号、异号)
两数相乘的积为负,这两个数
______ (同号、异号)
异号
同号
2.判断下列方程的解是正数还是负 数或0:
(1)4x=-16;
(2)-3x=18;
(3)-9x=-36;
(4)-5x=0.
1、两数相乘,同号得正,异号得负,
并把绝对值相乘。
2、任何数同0相乘,都得0。
3、有理数乘法运算顺序:
先确定积的符号,再确定积的绝对值
有理数的乘法,关键是确定积的符号,三个或三个以上的有理数相乘如何确定积的符号呢?
(-2)×3×4;
(-2)×(-3)×4;
(3) (-2)×(-3)×(-4)×5;
(4) (-2)×(-3)×(-4)×(-5);
(5) (-2)×(-3)×(-4)×(-5)×0.
作业布置:
1、练习册习题5.6/1、2、3题
2、一课一练5.7
