2021—2022学年华东师大版七年级数学上册第五章 相交线与平行线 测评卷(Word版含答案)
文档属性
| 名称 | 2021—2022学年华东师大版七年级数学上册第五章 相交线与平行线 测评卷(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 183.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 10:16:14 | ||
图片预览



文档简介
第5章测评卷
题号
一
二
三
总分
得分
选择题
1.下列各图中,∠1与∠2互为对顶角的是(
)
2.如图,∠1
与∠2是(
)
A.同位角
B.内错角
C.同旁内角
D.邻补角
第2题图
3.如图所示,点P到直线l的距离是(
)
A.线段PA的长度
B.线段PB的长度
C.线段PC的长度
D.线段PD的长度
第3题图
4.如图,直线a,b被直线c所藏,下列条件不能判定直线a与b平行的是(
)
A.∠1=∠3
B.∠2+∠4=
180°
C.∠1=∠4
D.∠3=∠4
第4题图
5.如图,直线a//b,直线c与直线a,b分别交于点D,E,射线DF⊥直线c,则图中与∠1互余的角有(
)
A.4个
B.3个
C.2个
D.1个
第5题图
6.已知△ABC中,BC=6,AC=3,CP⊥AB,垂足为P
,CP的长可能是(
)
A.
2
B.4
C.5
D.7
7.如图,直线AC//
BD,A0、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是(
)
A.∠BAO与∠CAO相等
B.∠BAC与∠ABD互补
C.∠BAO与∠ABO互余
D.∠ABO与∠DB0不等
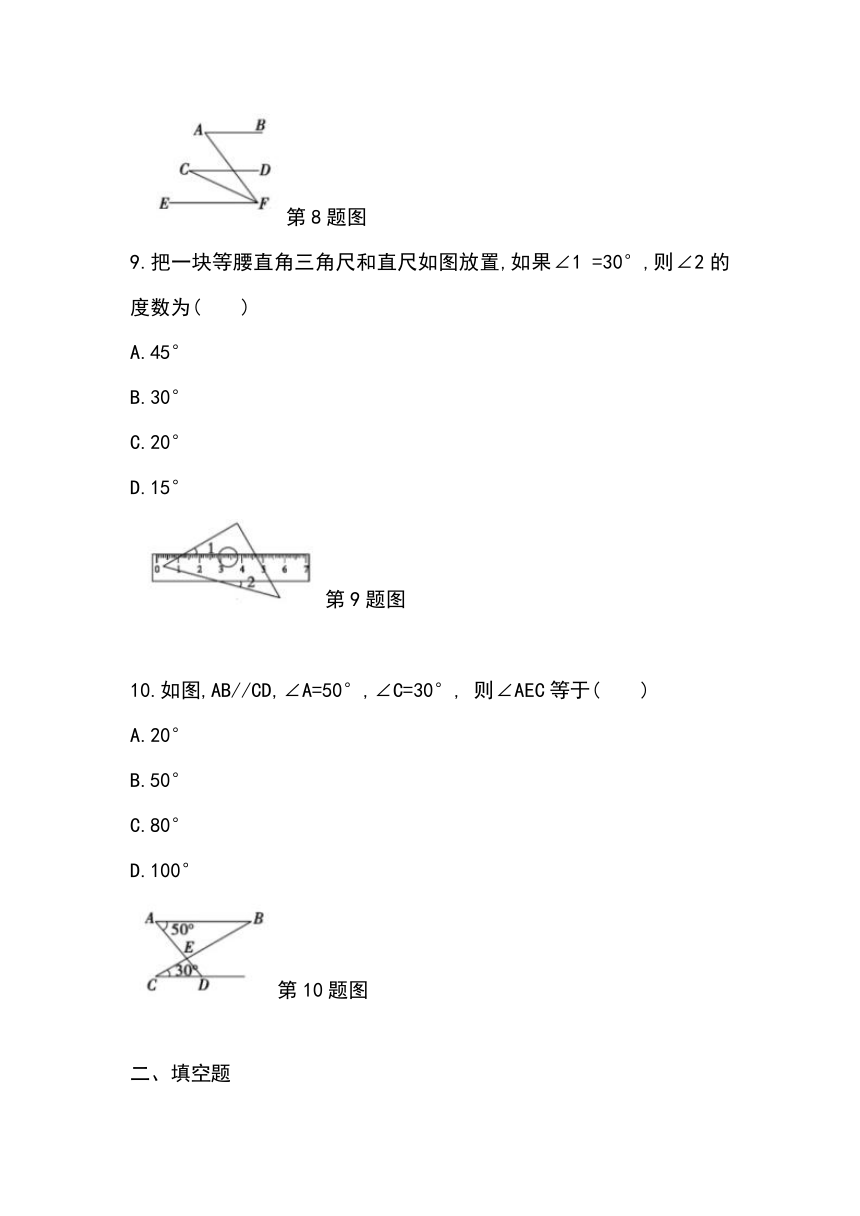
8.如图,已知AB//CD//EF,FC平分∠AFE,∠C=25°
,则∠A的度数是
(
)
A.
25°
B.35°
C.45°
D.50°
第8题图
9.把一块等腰直角三角尺和直尺如图放置,如果∠1
=30°,则∠2的度数为(
)
A.45°
B.30°
C.20°
D.15°
第9题图
10.如图,AB//CD,∠A=50°,∠C=30°,
则∠AEC等于(
)
A.20°
B.50°
C.80°
D.100°
第10题图
二、填空题
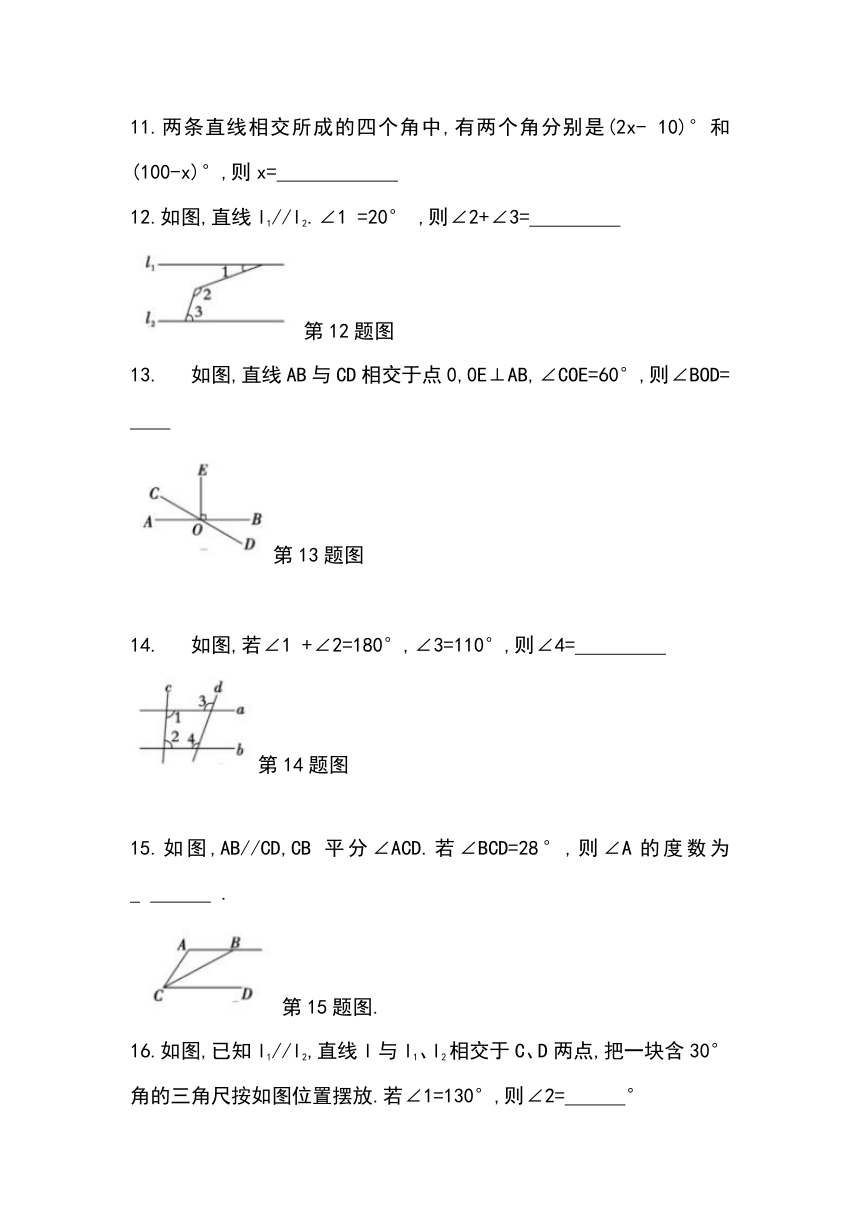
11.两条直线相交所成的四个角中,有两个角分别是(2x-
10)°和(100-x)°,则x=
12.如图,直线l1//l2.∠1
=20°
,则∠2+∠3=
第12题图
如图,直线AB与CD相交于点0,0E⊥AB,∠COE=60°,则∠BOD=
第13题图
如图,若∠1
+∠2=180°,∠3=110°,则∠4=
第14题图
15.如图,AB//CD,CB
平分∠ACD.若∠BCD=28°,则∠A的度数为_
.
第15题图.
16.如图,已知l1//l2,直线l与l1、l2相交于C、D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2=
°
第16题图
如图,AB⊥AC
,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有
条
第17题图
如图,直线a//b,∠P=75°,∠2=30°,则∠1=
.
第18题图.
三、解答题
19.
如图,在直线MN的异侧有A,B两点,按要求画图取点.并注明画图取点的依据.
(1)在直线MN上取一点c,使线段AC最短,依据是
;
(2)在直线MN上取一点D,使AD+
BD最短.依据是
20.
如图,AB//CD,点E是CD上一点,∠AEC=42°
,EF平分∠AED交AB于点F,求∠AFE的度数.
21.如图,AE与CD交于点0,∠A
=50°,0C
=
OE,∠C
=25°
,求证:AB//CD.
如图,已知直线AB和CD相交于点0,∠COE是直角,OF平分∠AOE,∠COF
=34°,求∠AOC和∠BOD的度数.
如图,已知l1//l2,C1在l1上,并且C1
A⊥l2,A为垂足,C2,C3,是l1上任意两点,点B在l2上,设△ABC1的面积是S1,
△ABC2的面积是S2,
△ABC3,的面积是S3,小颖认为S1
=S2
=S3,请你帮小颖说明理由.
24.
如图,BD⊥AC于D,EF⊥AC于F,∠AMD=
∠AGF,∠1
=
∠2=35°.
(1)求∠GFC的度数;
(2
)求证:DM//
BC.
答案:
B
C
B
D
A
A
D
D
D
C
40或80
200°
30°
110°
124°
20
5
45°
垂线段最短
两点之间线段最短
解:∵∠AEC=42。∴∠AED=
180°-∠AEC
=
138°
∵EF平分∠AED,∴∠DEF=∠AED=69°,
又∵
AB//CD,
∴∠AFE=∠DEF
=
69°.
解:
∵0C=0E,∴∠E=∠C=25°
,
∴∠COE=180°-∠C-∠E=
130°,
∴∠DOE=
180°-∠COE
=
180°-
130°
=
50°,
∵∠A=50°,∴∠A=∠DOE,
∴AB//
CD.
解:∵∠COE=90°,∠COF
=34°
∴∠EOF=∠COE-∠COF=56°
∵
OF平分∠AOE,
∴∠AOE=2∠EOF
=112°,
∴∠A0C=112°
-90°
=22°,
∵∠AOC=∠BOD,
∴∠BOD
=22°,
解:∵l1
//l2,
∴△ABC1,
△ABC2,△ABC3的底边AB上的高相等,
∴S1
=S2=S3.
(1)解:∵
BD⊥AC,EF⊥AC,
∴
BD//EF,
∴∠EFG=∠1=35°,∠GFC
=90°
+35°=
125°:
(2)证明:∵
BD//EF,∴∠2=∠CBD,
∴∠1=∠CBD.
∴
GF//
BC,
∵∠AMD=∠AGF,
∴MD//GF,∴DM//BC.
题号
一
二
三
总分
得分
选择题
1.下列各图中,∠1与∠2互为对顶角的是(
)
2.如图,∠1
与∠2是(
)
A.同位角
B.内错角
C.同旁内角
D.邻补角
第2题图
3.如图所示,点P到直线l的距离是(
)
A.线段PA的长度
B.线段PB的长度
C.线段PC的长度
D.线段PD的长度
第3题图
4.如图,直线a,b被直线c所藏,下列条件不能判定直线a与b平行的是(
)
A.∠1=∠3
B.∠2+∠4=
180°
C.∠1=∠4
D.∠3=∠4
第4题图
5.如图,直线a//b,直线c与直线a,b分别交于点D,E,射线DF⊥直线c,则图中与∠1互余的角有(
)
A.4个
B.3个
C.2个
D.1个
第5题图
6.已知△ABC中,BC=6,AC=3,CP⊥AB,垂足为P
,CP的长可能是(
)
A.
2
B.4
C.5
D.7
7.如图,直线AC//
BD,A0、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是(
)
A.∠BAO与∠CAO相等
B.∠BAC与∠ABD互补
C.∠BAO与∠ABO互余
D.∠ABO与∠DB0不等
8.如图,已知AB//CD//EF,FC平分∠AFE,∠C=25°
,则∠A的度数是
(
)
A.
25°
B.35°
C.45°
D.50°
第8题图
9.把一块等腰直角三角尺和直尺如图放置,如果∠1
=30°,则∠2的度数为(
)
A.45°
B.30°
C.20°
D.15°
第9题图
10.如图,AB//CD,∠A=50°,∠C=30°,
则∠AEC等于(
)
A.20°
B.50°
C.80°
D.100°
第10题图
二、填空题
11.两条直线相交所成的四个角中,有两个角分别是(2x-
10)°和(100-x)°,则x=
12.如图,直线l1//l2.∠1
=20°
,则∠2+∠3=
第12题图
如图,直线AB与CD相交于点0,0E⊥AB,∠COE=60°,则∠BOD=
第13题图
如图,若∠1
+∠2=180°,∠3=110°,则∠4=
第14题图
15.如图,AB//CD,CB
平分∠ACD.若∠BCD=28°,则∠A的度数为_
.
第15题图.
16.如图,已知l1//l2,直线l与l1、l2相交于C、D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2=
°
第16题图
如图,AB⊥AC
,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有
条
第17题图
如图,直线a//b,∠P=75°,∠2=30°,则∠1=
.
第18题图.
三、解答题
19.
如图,在直线MN的异侧有A,B两点,按要求画图取点.并注明画图取点的依据.
(1)在直线MN上取一点c,使线段AC最短,依据是
;
(2)在直线MN上取一点D,使AD+
BD最短.依据是
20.
如图,AB//CD,点E是CD上一点,∠AEC=42°
,EF平分∠AED交AB于点F,求∠AFE的度数.
21.如图,AE与CD交于点0,∠A
=50°,0C
=
OE,∠C
=25°
,求证:AB//CD.
如图,已知直线AB和CD相交于点0,∠COE是直角,OF平分∠AOE,∠COF
=34°,求∠AOC和∠BOD的度数.
如图,已知l1//l2,C1在l1上,并且C1
A⊥l2,A为垂足,C2,C3,是l1上任意两点,点B在l2上,设△ABC1的面积是S1,
△ABC2的面积是S2,
△ABC3,的面积是S3,小颖认为S1
=S2
=S3,请你帮小颖说明理由.
24.
如图,BD⊥AC于D,EF⊥AC于F,∠AMD=
∠AGF,∠1
=
∠2=35°.
(1)求∠GFC的度数;
(2
)求证:DM//
BC.
答案:
B
C
B
D
A
A
D
D
D
C
40或80
200°
30°
110°
124°
20
5
45°
垂线段最短
两点之间线段最短
解:∵∠AEC=42。∴∠AED=
180°-∠AEC
=
138°
∵EF平分∠AED,∴∠DEF=∠AED=69°,
又∵
AB//CD,
∴∠AFE=∠DEF
=
69°.
解:
∵0C=0E,∴∠E=∠C=25°
,
∴∠COE=180°-∠C-∠E=
130°,
∴∠DOE=
180°-∠COE
=
180°-
130°
=
50°,
∵∠A=50°,∴∠A=∠DOE,
∴AB//
CD.
解:∵∠COE=90°,∠COF
=34°
∴∠EOF=∠COE-∠COF=56°
∵
OF平分∠AOE,
∴∠AOE=2∠EOF
=112°,
∴∠A0C=112°
-90°
=22°,
∵∠AOC=∠BOD,
∴∠BOD
=22°,
解:∵l1
//l2,
∴△ABC1,
△ABC2,△ABC3的底边AB上的高相等,
∴S1
=S2=S3.
(1)解:∵
BD⊥AC,EF⊥AC,
∴
BD//EF,
∴∠EFG=∠1=35°,∠GFC
=90°
+35°=
125°:
(2)证明:∵
BD//EF,∴∠2=∠CBD,
∴∠1=∠CBD.
∴
GF//
BC,
∵∠AMD=∠AGF,
∴MD//GF,∴DM//BC.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
