菱形的性质(两课时)无答案
文档属性
| 名称 | 菱形的性质(两课时)无答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 107.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-26 00:00:00 | ||
图片预览



文档简介
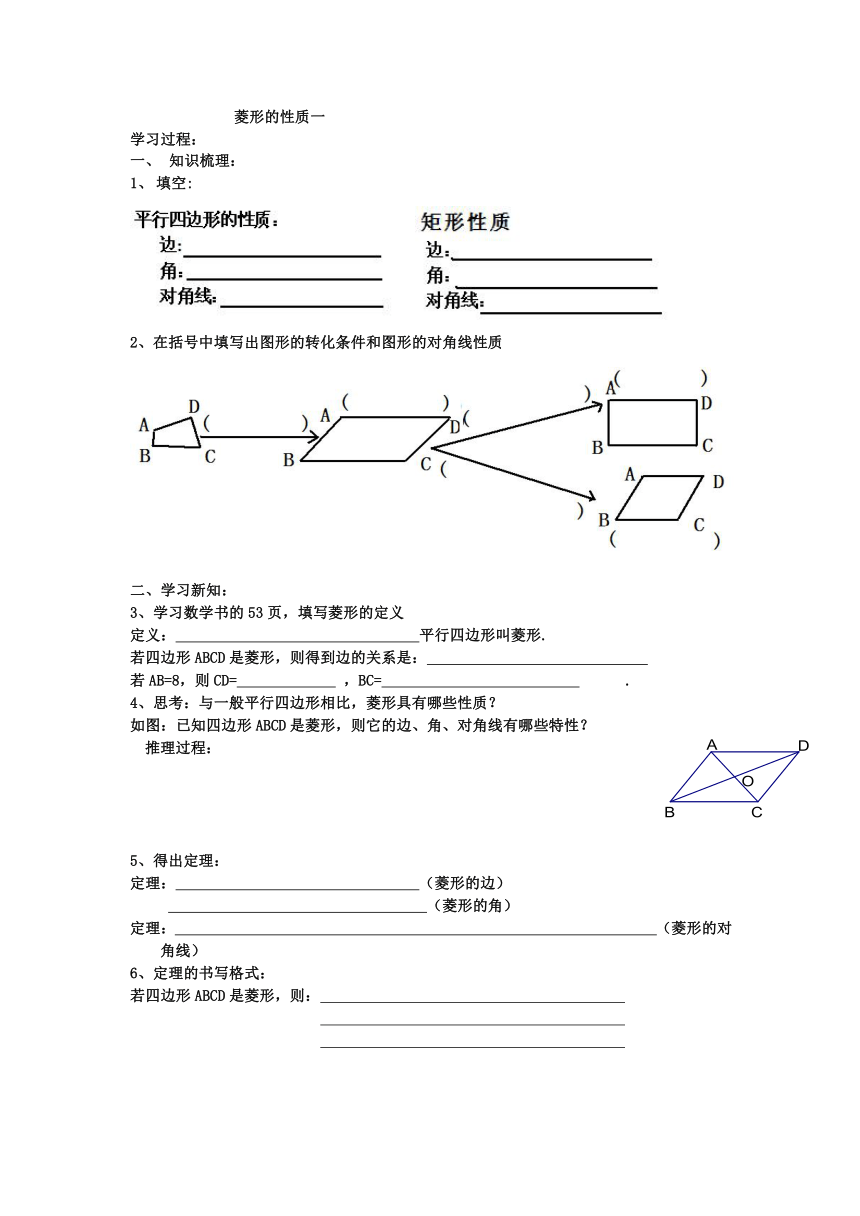
菱形的性质一
学习过程:
知识梳理:
填空:
2、在括号中填写出图形的转化条件和图形的对角线性质
二、学习新知:
3、学习数学书的53页,填写菱形的定义
定义: 平行四边形叫菱形.
若四边形ABCD是菱形,则得到边的关系是:
若AB=8,则CD= ,BC= .
4、思考:与一般平行四边形相比,菱形具有哪些性质?
如图:已知四边形ABCD是菱形,则它的边、角、对角线有哪些特性?
推理过程:
5、得出定理:
定理: (菱形的边)
(菱形的角)
定理: (菱形的对角线)
6、定理的书写格式:
若四边形ABCD是菱形,则:
三、定理的运用:
例1:如图,已知菱形ABCD的周长为20cm,∠A:∠ABC=1:2,
求∠ABD的度数与BD长。
解:
例2:已知菱形的两条对角线长分别为6和8,则它的边长为多少?
解:
四、小结
菱形的边和对角线有不同于一般的平行四边形的性质,有关菱形的几何计算问题可以化为特殊三角形(直角三角形、等腰三角形),利用特殊三角形的性质来计算。
五、达标练习:
菱形的对角线长为24和10,则菱形的边长为 ,周长为 .
已知菱形两邻角的比是1:2,周长为40cm,则较短对角线的长是 .
已知菱形的一条对角线与边长相等,则菱形的邻角度数分别为 ( )
A. 45°,135° B. 60°,120°
C. 90°,90° D. 30°,150°
已知,如图所示,菱形ABCD中,E,F分别是BC、CD上的一点,∠D=∠EAF=∠AEF=60°.∠BAE=18°,求∠CEF的度数.
5:菱形的边长是2 cm,一条对角线的长是2 cm,求另一条对角线的长。
五:作业:
1.(09河北)如图,在菱形ABCD中,AB = 5,∠BCD = 120°,则对角线AC等于( )
A.20 B.15 C.10 D.5
2.己知:如图,菱形ABCD中,∠B=600,AB=4,则以AC为边长的正方形ACEF的周长为 .
3.已知四边形ABCD是菱形,O是两条对角线的交点,AC=8cm,DB=6cm,这个菱形的边长是________cm.
写过程:
4.已知菱形的边长是5cm,一条对角线长为8cm,则另一条对角线长为______cm.
写过程:
5、菱形ABCD,若∠A:∠B=2:1,∠CAD的平分线AE和边CD之间的关系是( )
A.相等 B.互相垂直且不平分 C.互相平分且不垂直 D.垂直且平分
6、已知菱形的周长为40cm,两对角线的长度之比为3:4,则两对角线的长分别为( )
A.6cm,8cm B.3cm,4cm C.12cm,16cm D.24cm,32cm
7、 已知菱形的周长为20cm,一条对角线长为5cm,求菱形各个角的度数.
已知菱形的一边与两条对角线构成的两角之比为5:4,求菱形的各内角的度数.
9、 如图3个全等的菱形构成的活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间 的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间 的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?
菱形的性质二
学习目标:
1、学习菱形的面积求法
1、会菱形的性质与面积公式进行计算;
3、在进行探索、猜想、证明的过程中,进一步发展推理论证的能力。
学习重、难点
重点:菱形的面积公式推导与运用
难点:性质定理、面积公式的运用 生活数学与理论数学的相互转化
学习过程:
一、前提测评(填空或选择):
1、 的平行四边形是菱形;菱形的 都相等,菱形的对角线 ,并且每一条对角线平分
2、 若菱形的一条对角线的长和边长相等,则菱形较小的内角是 度
3、 菱形具有而平行四边形不一定具有的性质为( )
A 对角线互相平分 B 邻角互补 C 对角相等 D 每条对角线平分一组对角
4、菱形的对角线长为24和10,菱形的边长
二、新知学习过程: (探讨求菱形面积方法)
由于菱形是特殊的平行四边形,因此可以利用平行四边形的面积求法来计算菱形的面积。
如图:菱形ABCD,AE⊥BC,AF⊥CD,
则, S 菱形ABCD= 或S菱形ABCD =
图1 图2
(1)如图1,若AB=6,AE=5,则S 菱形ABCD =
(2)已知菱形的面积等于80cm2,高等于8cm,则菱形的周长为 .
2、已知菱形ABCD,对角线AC、BD交于点O,
求证:(1)△ABO≌△AOD≌△BOC≌△DOC
(2) S 菱形ABCD =AC.BD
结论:菱形的面积等于 的 一半.
(1)、菱形的两条对角线分别为6和10,则菱形的面积为 .
(2)若菱形的一条对角线的长为12cm,面积是30cm2,则这个菱形的另一条对角线
的长为 cm.
例1、如图,已知菱形ABCD的对角线交于点O,AC=16cm,BD=12cm,求菱形的高.
已知菱形ABCD的边长为2 cm,∠BAD=120°对角线AC、BD相交于点O,试求出菱形对角线的长和面积.
三、课堂练习:
1.四边形ABCD是菱形,∠ABC=120°,AB=12cm,则∠ABD的度数为_____,∠DAB的度数为______;对角线BD=_______,AC=_______;菱形ABCD的面积为_______.
2、菱形的两条对角线分别为4和7,则菱形的面积为 .
3、菱形的两邻角之比为1:2,边长为2,则菱形的面积为__________.
4、已知菱形ABCD的周长为40cm,BD=AC,则菱形的面积为( )
A.96cm2 B.94cm2 C.92cm2 D.90cm2
3.(09南宁)如图2,将一个长为10cm,宽为8cm的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )
A. B. C. D.
第3题图
四、小结:
五、作业:
1.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点E,交AB于点F,F为垂足,连接DE,则∠CDE=_________
在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,(如图)则∠EAF等于( )
A.75° B.60° C.45° D.30°
3、如图,菱形ABCD的周长为20cm,对角线AC、BD相交于点O ,其中BD=8cm.求对角线BD的长和菱形ABCD的面积.
4、如图是菱形花坛ABCD,它的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积.
5.求证:菱形的对角线的交点到各边的距离相等。
6、在菱形中,对角线与相交于点,.过点作交的延长线于点.
(1)求的周长;
(2)点为线段上的点,连接并延长交于点.
求证:.
B
A
C
D
1题
2题
A
B
C
D
A
Q
D
E
B
P
C
O
学习过程:
知识梳理:
填空:
2、在括号中填写出图形的转化条件和图形的对角线性质
二、学习新知:
3、学习数学书的53页,填写菱形的定义
定义: 平行四边形叫菱形.
若四边形ABCD是菱形,则得到边的关系是:
若AB=8,则CD= ,BC= .
4、思考:与一般平行四边形相比,菱形具有哪些性质?
如图:已知四边形ABCD是菱形,则它的边、角、对角线有哪些特性?
推理过程:
5、得出定理:
定理: (菱形的边)
(菱形的角)
定理: (菱形的对角线)
6、定理的书写格式:
若四边形ABCD是菱形,则:
三、定理的运用:
例1:如图,已知菱形ABCD的周长为20cm,∠A:∠ABC=1:2,
求∠ABD的度数与BD长。
解:
例2:已知菱形的两条对角线长分别为6和8,则它的边长为多少?
解:
四、小结
菱形的边和对角线有不同于一般的平行四边形的性质,有关菱形的几何计算问题可以化为特殊三角形(直角三角形、等腰三角形),利用特殊三角形的性质来计算。
五、达标练习:
菱形的对角线长为24和10,则菱形的边长为 ,周长为 .
已知菱形两邻角的比是1:2,周长为40cm,则较短对角线的长是 .
已知菱形的一条对角线与边长相等,则菱形的邻角度数分别为 ( )
A. 45°,135° B. 60°,120°
C. 90°,90° D. 30°,150°
已知,如图所示,菱形ABCD中,E,F分别是BC、CD上的一点,∠D=∠EAF=∠AEF=60°.∠BAE=18°,求∠CEF的度数.
5:菱形的边长是2 cm,一条对角线的长是2 cm,求另一条对角线的长。
五:作业:
1.(09河北)如图,在菱形ABCD中,AB = 5,∠BCD = 120°,则对角线AC等于( )
A.20 B.15 C.10 D.5
2.己知:如图,菱形ABCD中,∠B=600,AB=4,则以AC为边长的正方形ACEF的周长为 .
3.已知四边形ABCD是菱形,O是两条对角线的交点,AC=8cm,DB=6cm,这个菱形的边长是________cm.
写过程:
4.已知菱形的边长是5cm,一条对角线长为8cm,则另一条对角线长为______cm.
写过程:
5、菱形ABCD,若∠A:∠B=2:1,∠CAD的平分线AE和边CD之间的关系是( )
A.相等 B.互相垂直且不平分 C.互相平分且不垂直 D.垂直且平分
6、已知菱形的周长为40cm,两对角线的长度之比为3:4,则两对角线的长分别为( )
A.6cm,8cm B.3cm,4cm C.12cm,16cm D.24cm,32cm
7、 已知菱形的周长为20cm,一条对角线长为5cm,求菱形各个角的度数.
已知菱形的一边与两条对角线构成的两角之比为5:4,求菱形的各内角的度数.
9、 如图3个全等的菱形构成的活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间 的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间 的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?
菱形的性质二
学习目标:
1、学习菱形的面积求法
1、会菱形的性质与面积公式进行计算;
3、在进行探索、猜想、证明的过程中,进一步发展推理论证的能力。
学习重、难点
重点:菱形的面积公式推导与运用
难点:性质定理、面积公式的运用 生活数学与理论数学的相互转化
学习过程:
一、前提测评(填空或选择):
1、 的平行四边形是菱形;菱形的 都相等,菱形的对角线 ,并且每一条对角线平分
2、 若菱形的一条对角线的长和边长相等,则菱形较小的内角是 度
3、 菱形具有而平行四边形不一定具有的性质为( )
A 对角线互相平分 B 邻角互补 C 对角相等 D 每条对角线平分一组对角
4、菱形的对角线长为24和10,菱形的边长
二、新知学习过程: (探讨求菱形面积方法)
由于菱形是特殊的平行四边形,因此可以利用平行四边形的面积求法来计算菱形的面积。
如图:菱形ABCD,AE⊥BC,AF⊥CD,
则, S 菱形ABCD= 或S菱形ABCD =
图1 图2
(1)如图1,若AB=6,AE=5,则S 菱形ABCD =
(2)已知菱形的面积等于80cm2,高等于8cm,则菱形的周长为 .
2、已知菱形ABCD,对角线AC、BD交于点O,
求证:(1)△ABO≌△AOD≌△BOC≌△DOC
(2) S 菱形ABCD =AC.BD
结论:菱形的面积等于 的 一半.
(1)、菱形的两条对角线分别为6和10,则菱形的面积为 .
(2)若菱形的一条对角线的长为12cm,面积是30cm2,则这个菱形的另一条对角线
的长为 cm.
例1、如图,已知菱形ABCD的对角线交于点O,AC=16cm,BD=12cm,求菱形的高.
已知菱形ABCD的边长为2 cm,∠BAD=120°对角线AC、BD相交于点O,试求出菱形对角线的长和面积.
三、课堂练习:
1.四边形ABCD是菱形,∠ABC=120°,AB=12cm,则∠ABD的度数为_____,∠DAB的度数为______;对角线BD=_______,AC=_______;菱形ABCD的面积为_______.
2、菱形的两条对角线分别为4和7,则菱形的面积为 .
3、菱形的两邻角之比为1:2,边长为2,则菱形的面积为__________.
4、已知菱形ABCD的周长为40cm,BD=AC,则菱形的面积为( )
A.96cm2 B.94cm2 C.92cm2 D.90cm2
3.(09南宁)如图2,将一个长为10cm,宽为8cm的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )
A. B. C. D.
第3题图
四、小结:
五、作业:
1.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点E,交AB于点F,F为垂足,连接DE,则∠CDE=_________
在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,(如图)则∠EAF等于( )
A.75° B.60° C.45° D.30°
3、如图,菱形ABCD的周长为20cm,对角线AC、BD相交于点O ,其中BD=8cm.求对角线BD的长和菱形ABCD的面积.
4、如图是菱形花坛ABCD,它的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积.
5.求证:菱形的对角线的交点到各边的距离相等。
6、在菱形中,对角线与相交于点,.过点作交的延长线于点.
(1)求的周长;
(2)点为线段上的点,连接并延长交于点.
求证:.
B
A
C
D
1题
2题
A
B
C
D
A
Q
D
E
B
P
C
O
