2021-2022学年北师大版九年级数学上册 1.2矩形的性质与判定 提升训练(Word版 附答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册 1.2矩形的性质与判定 提升训练(Word版 附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 00:00:00 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学上册《1.2矩形的性质与判定》
能力达标专题提升训练(附答案)
一.选择题
1.如图,矩形ABCD中,点G是AD的中点,GE⊥BG交CD于点E,CB=CE,连接CG交BE于点F,则∠ECF的度数为( )
A.30°
B.22.5°
C.25°
D.15°
2.如图,在矩形ABCD中,E是AB的中点,动点F从点B出发,沿BC运动到点C时停止,以EF为边作?EFGH,且点G、H分别在CD、AD上.在动点F运动的过程中,?EFGH的面积( )
A.逐渐增大
B.逐渐减小
C.不变
D.先增大,再减小
3.已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥BD于点E,PF⊥AC于点F,则PE+PF等于( )
A.
B.
C.
D.
4.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=( )
A.60°
B.45°
C.30°
D.22.5°
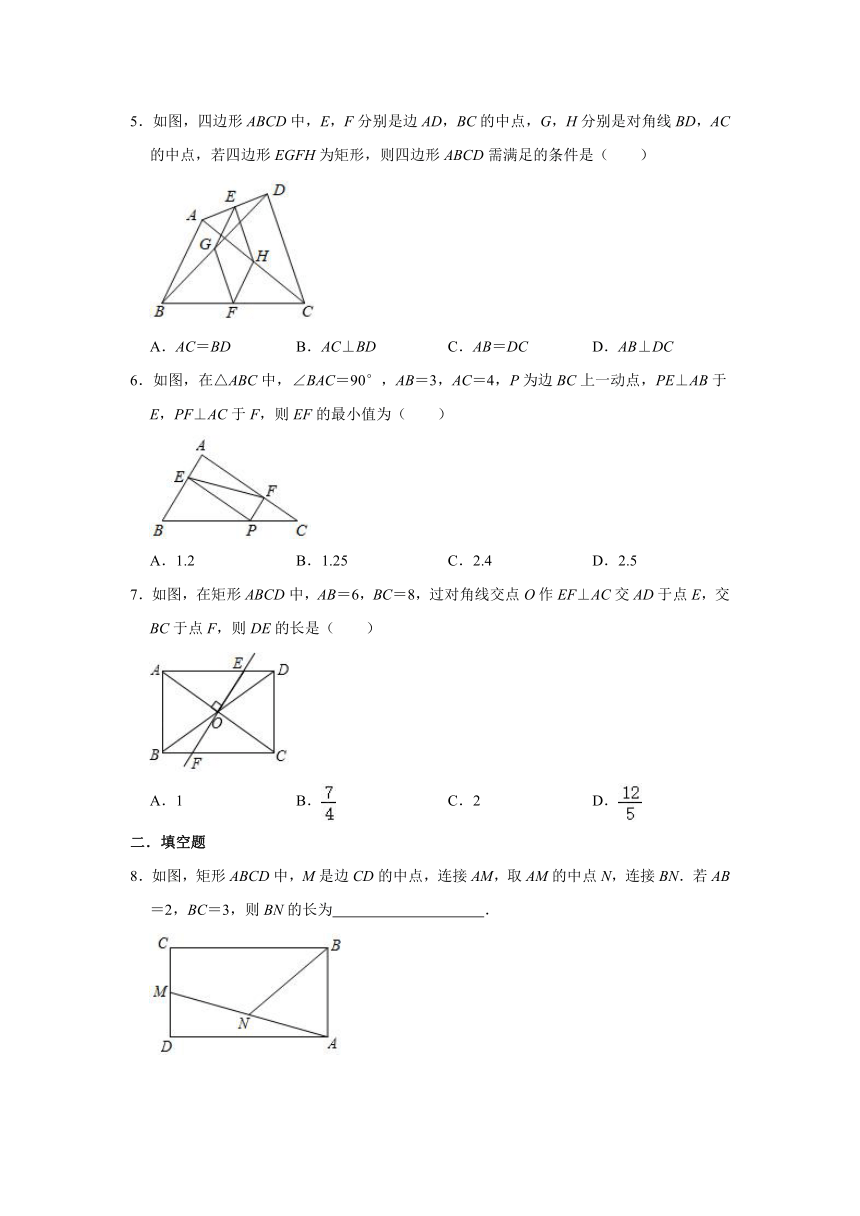
5.如图,四边形ABCD中,E,F分别是边AD,BC的中点,G,H分别是对角线BD,AC的中点,若四边形EGFH为矩形,则四边形ABCD需满足的条件是( )
A.AC=BD
B.AC⊥BD
C.AB=DC
D.AB⊥DC
6.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )
A.1.2
B.1.25
C.2.4
D.2.5
7.如图,在矩形ABCD中,AB=6,BC=8,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE的长是( )
A.1
B.
C.2
D.
二.填空题
8.如图,矩形ABCD中,M是边CD的中点,连接AM,取AM的中点N,连接BN.若AB=2,BC=3,则BN的长为
.
9.如图,矩形ABCD中,AB=3,BC=4,DE平分∠ADC交BC于点E,AF平分∠BAD交BC于点F,交DE于点G,则=
.
10.如图,长方形ABCD中,AD=20,AB=8,点Q是BC的中点,点P在AD边上运动,当△BPQ是等腰三角形时,AP的长为
.
11.如图,F是矩形ABCD内一点,AF=BF,连接DF并延长交BC于点G,且点C与AB的中点E恰好关于直线DG对称,若AD=6,则AB的长为
.
12.如图,矩形ABCD的对角线AC与BD交于点O,点E在AD上,且DE=CD,连接OE,BE,AC与BE相交于点F,∠ABE=∠ACB,则下列结论:①BE=DE;②OE⊥BD;③△AEF是等腰三角形;④当AE=2,则OE的长为,其中正确的结论是
.(填写所有正确结论的序号)
13.如图,M为矩形ABCD中AD边中点,E、F分别为BC、CD上的动点,且BE=2DF,若AB=1,BC=2,则ME+2AF的最小值为
.
三.解答题
14.如图,在矩形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.过点C作CF∥BD交线段OE的延长线于点F,连接DF.
求证:(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
15.如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
16.已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于点O.
(1)求证:OE=OF;
(2)若点O为CD的中点,求证:四边形DECF是矩形.
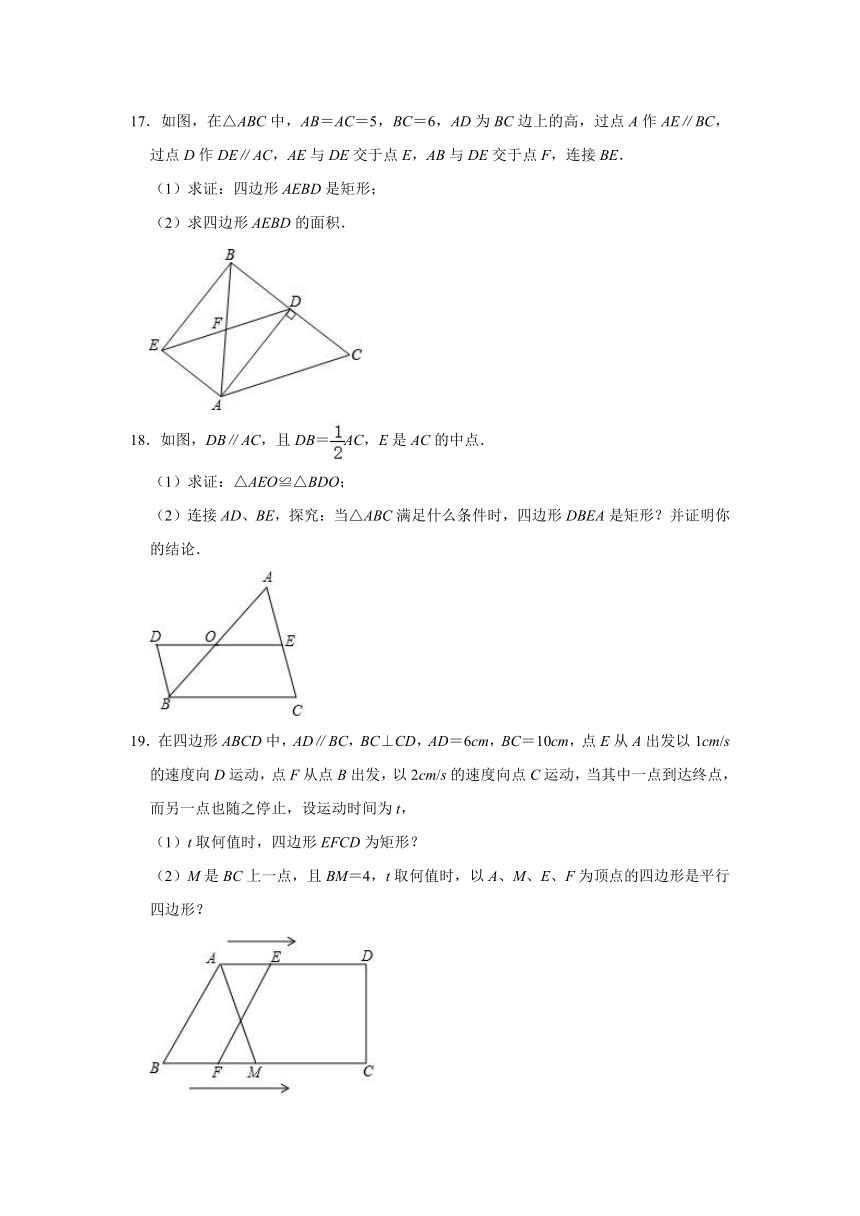
17.如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连接BE.
(1)求证:四边形AEBD是矩形;
(2)求四边形AEBD的面积.
18.如图,DB∥AC,且DB=AC,E是AC的中点.
(1)求证:△AEO≌△BDO;
(2)连接AD、BE,探究:当△ABC满足什么条件时,四边形DBEA是矩形?并证明你的结论.
19.在四边形ABCD中,AD∥BC,BC⊥CD,AD=6cm,BC=10cm,点E从A出发以1cm/s的速度向D运动,点F从点B出发,以2cm/s的速度向点C运动,当其中一点到达终点,而另一点也随之停止,设运动时间为t,
(1)t取何值时,四边形EFCD为矩形?
(2)M是BC上一点,且BM=4,t取何值时,以A、M、E、F为顶点的四边形是平行四边形?
20.如图,在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠DAB,CF=3,BF=4,求DF长.
21.如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.
(1)依题意,补全图形;
(2)求证:四边形EFMN是矩形;
(3)连接DM,若DM⊥AC于点M,ON=3,求矩形ABCD的面积.
参考答案
一.选择题
1.解:取BE的中点O,连接OG,OC,
∵O,G为中点,
∴OG为四边形ADEB的中位线,
∴AB∥OG∥DE,
∴∠OGC=∠ECF,
∵CE=BC,∠BCE=90°,
∴△BCE是等腰直角三角形,
∴∠CBE=∠BEC=45°,
∵∠BCE=90°,O为BE的中点,
∴OC=OE=BE,
∴∠OCE=∠OEC=45°,
∵GE⊥BG,O为BE的中点,
∴OG=BE,
∴OG=OC,
∴∠OGC=∠OCG,
∴∠OCG=∠ECF=∠OCE=22.5°,
故选:B.
2.解:设AB=a,BC=b,BE=c,BF=x,
连接EG,
∵四边形EFGH为平行四边形,
∴EF=HG,EF∥HG,
∴∠FEG=∠HGE,
∵四边形ABCD为矩形,
∴AB∥CD,
∴∠BEG=∠DGE,
∴∠BEG﹣∠FEG=∠DGE﹣∠EGH,
∴∠BEF=∠HGD
∵EF=HG,∠B=∠D,
∴Rt△BEF≌Rt△DGH(AAS),
同理Rt△AEH≌Rt△GFC,
∴S平行四边形EFGH=S矩形ABCD﹣2(S△BEF+S△AEH)
=ab﹣2[cx+(a﹣c)(b﹣x)]
=ab﹣(cx+ab﹣ax﹣bc+cx)
=ab﹣cx﹣ab+ax+bc﹣cx
=(a﹣2c)x+bc,
∵E是AB的中点,
∴a=2c,
∴a﹣2c=0,
∴S平行四边形EFGH=bc=ab,
故选:C.
3.解:连接PO,
∵矩形ABCD的两边AB=5,BC=12,
∴S矩形ABCD=AB?BC=60,OA=OC,OB=OD,AC=BD,AC===13,
∴S△AOD=S矩形ABCD=15,OA=OD=AC=,
∴S△AOD=S△AOP+S△DOP=OA?PE+OD?PF=OA(PE+PF)=××(PE+PF)=15,
∴PE+PF=,
故选:C.
4.解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC,OB=OD,
∴OA=OB═OC,
∴∠OAD=∠ODA,∠OAB=∠OBA,
∴∠AOE=∠OAD+∠ODA=2∠OAD,
∵∠EAC=2∠CAD,
∴∠EAO=∠AOE,
∵AE⊥BD,
∴∠AEO=90°,
∴∠AOE=45°,
∴∠OAB=∠OBA=(180°﹣45°)=67.5°,
∴∠BAE=∠OAB﹣∠OAE=22.5°.
故选:D.
5.解:若四边形EGFH为矩形,则四边形ABCD需满足的条件是AB⊥DC,理由如下:
∵E,G分别是AD,BD的中点,
∴EG是△DAB的中位线,
∴EG=AB,EG∥AB,
同理,FH=AB,FH∥AB,GF∥DC,
∴EG=FH,EG∥FH,
∴四边形EGFH是平行四边形,
∵AB⊥DC,GF∥DC,FH∥AB,
∴GF⊥FH,
∴∠GFH=90°,
∴平行四边形EGFH是矩形,
故选:D.
6.解:连接AP,如图:
∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=90°,
∵∠BAC=90°,
∴四边形AFPE是矩形,
∴EF=AP,
要使EF最小,只要AP最小即可,
当AP⊥BC时,AP最短,
∵∠BAC=90°,AB=3,AC=4,
∴BC===5,
∵△ABC的面积=×4×3=×5×AP,
∴AP=2.4,
即EF=2.4,
故选:C.
7.解:连接CE,如图所示:
∵四边形ABCD是矩形,
∴∠ADC=90°,CD=AB=6,AD=BC=8,OA=OC,
∵EF⊥AC,
∴AE=CE,
设DE=x,则CE=AE=8﹣x,
在Rt△CDE中,由勾股定理得:x2+62=(8﹣x)2,
解得:x=,
即DE=;
故选:B.
二.填空题
8.解:过点N作GH∥AB,分别交BC于点G,交AD于点H,如图,
∵矩形ABCD,
∴AB=CD,AD=BC,∠C=∠ABG=90°,AB∥CD,
∴四边形CDHG,四边形GHAB为矩形,
∴∠BGN=90°,GH=CD=AB,GH∥CD∥AB,
∵N为AM中点,
∴MN=AN,DH=HA,
∴CG=GB=BC=,H为DA的中点,
∴NH为△AMD的中位线,
∴NH=MD,
∵M是CD的中点,
∴MD=CD=AB=1,
∴NH=,
∴GN=GH﹣NH=AB﹣NH=,
在Rt△BGN中,由勾股定理得,
BN==,
故答案为:.
9.解:如图,过点G作AD的垂线,分别交AD,BC于点N,M,
则四边形CDNM是矩形,
∴MN=CD=AB=3,CM=DN,
∵四边形ABCD是矩形,
∴AD∥BC,BC=AD=4,
∵DE平分∠ADC交BC于点E,AF平分∠BAD交BC于点F,
∴∠DAG=∠ADG=∠GEF=∠GFE=45°,
∴△AGD和△GEF均为等腰直角三角形,
∴GN=DN=AD=2,
∴GM=MN﹣GN=AB﹣GN=3﹣2=1,
MC=DN=2,
∴MF=GM=1,
∴CG===,
∴GF=,
∴==.
故答案为:.
10.解:∵四边形ABCD为矩形,AD=20,
∴BQ=10,
①当BP=PQ时,过P作PM⊥BQ,交BQ于点M,如图1所示:
则BM=MQ=5,且四边形ABMP为矩形,
∴AP=BM=5,
②当BQ=BP时,则BP=10,在Rt△ABP中,AB=8,由勾股定理可求得AP=6,
③当PQ=BQ时,
过Q作QN⊥RS,交RS于点N,则可知RN=SN,
在Rt△RNQ中,可求得RN=SN=6,
则AR=4,AS=16,
即R、S为满足条件的P点的位置,
∴AP=4或16,
综上可知AP为4或5或6或16,
故答案为:4或5或6或16.
11.解:连接EF、EG、EC,如图所示:
∵四边形ABCD是矩形,
∴BC=AD=6,AD∥BC,∠BAD=∠ABC=90°,
∴AB⊥AD,
∵AF=BF,点E是AB的中点,
∴EF⊥AB,AB=2BE,AE=BE,
∴∠AEF=∠ABC=90°,
∴EF∥BC,
∴EF∥AD∥BC,
∴DF=FG,
在Rt△DCG中,CF为斜边DG上的中线,
∴CF=DG=FG,
∵EF∥GC,
∴∠OEF=∠OCG,∠OFE=∠OGC,
∵点C与AB的中点E关于直线DG对称,
∴DG垂直平分线段EC,
∴FG⊥CE,EO=CO,EF=CF,
在△OEF和△OCG中,
,
∴△OEF≌△OCG(AAS),
∴EF=CG,
∴CF=FG=CG,
∴△CGF是等边三角形,
∴∠GCF=60°,
∵CO⊥GF,
∴CO平分∠GCF,
∴∠GCO=GCF=30°,
在Rt△BCE中,∠EBC=90°,∠BCE=30°,BC=6,
∴CE=2BE,
∴BE===2.
∴AB=2BE=4;
故答案为:4.
12.解:∵四边形ABCD是矩形,
∴AB=CD,∠BAE=90°,
∵DE=CD,
∴AB=DE,
∵AB<BE,
∴BE≠DE,故①错误;
∵BO=DO,BE≠DE,
∴OE与BD不垂直,故②错误;
如图,作CH⊥BE于H,EG⊥BD于G.设BE与AC的交点为F.
则∠HBC+∠BCH=∠BHC=90°,
∵四边形ABCD为矩形,
∴AD=BC,AB=CD,∠ABC=∠BAD=90°,AD∥BC,AC=BD
∴∠ABE+∠CBH=90°,
∴∠ABE=∠BCH,
∵∠ABE=∠ACB,
∴∠BCH=∠GCH,
∴BH=FH,BC=CG,∠CBH=∠CGH,
设AB=x,则ED=CD=AB=x,
∵AE=2,所以AD=AE+ED=2+x,
∴CB=CF=2+x,
∵AD∥BC,
∴∠AEG=∠CBH=∠CGH=∠AGE,
∴AF=AE=2,故③正确;
∴AC=AG+CG=4+x,
在Rt△ABC中:AB2+BC2=AC2,
∴x2+(x+2)2=(x+4)2,解得x1=6,x2=﹣2(舍),
∴AB=CD=6,AD=AC=8,AC=BD=10,
∵AC与BD交于点O,
∴AO=BO=CO=DO=5,
∴EG=ED=,DG=ED=,
∴OG=OD﹣DG=5﹣=,
在Rt△OGE中:
OE2=EG2+OG2=()2+()2==13,
∴OE=,故④正确.
故其中正确的结论是③④.
故答案为:③④.
13.解:如图,过点M作MH⊥BC于H.设DF=x,则BE=2x.
∵四边形ABCD是矩形,
∴∠BAD=∠B=∠D=90°,
∵MH⊥BC,
∴∠MHB=90°,
∴四边形ABHM是矩形,
∴AM=DM=BH=1,AB=MH=1,
∴EH=1﹣2x,
∴ME+2AF=+2=+,
欲求ME+2AF的最小值,相当于在x轴上找一点Q(2x,0),使得点Q到J(0,4),和K(1,1)的距离之和最小(如下图),
作点J关于x轴的对称点J′,连接KJ′交x轴于Q,连接JQ,此时JQ+QK的值最小,最小值=KJ′,
∵J′(0,﹣4),K(1,1),
∴KJ′==,
∴ME+2AF的最小值为,
故答案为.
三.解答题
14.证明:(1)∵CF∥BD,
∴∠ODE=∠FCE,
∵E是CD中点,
∴CE=DE,
在△ODE和△FCE中,
,
∴△ODE≌△FCE(ASA);
(2)∵△ODE≌△FCE,
∴OD=FC,
∵CF∥BD,
∴四边形ODFC是平行四边形,
在矩形ABCD中,OC=OD,
∴四边形ODFC是菱形.
15.(1)证明:∵四边形ABCD是矩形,
∴AB=DC,∠A=∠D=90°,
∵M为AD中点,
∴AM=DM,
在△ABM和△DCM,
,
∴△ABM≌△DCM(SAS);
(2)四边形MENF是菱形.
证明如下:∵N、E、F分别是BC、BM、CM的中点,
∴NE∥CM,NE=CM,MF=CM,
∴NE=FM,NE∥FM,
∴四边形MENF是平行四边形,
由(1)知△ABM≌△DCM,
∴BM=CM,
∵E、F分别是BM、CM的中点,
∴ME=MF,
∴平行四边形MENF是菱形;
16.证明:
(1)∵CE平分∠BCD、CF平分∠GCD,
∴∠BCE=∠DCE,∠DCF=∠GCF,
∵EF∥BC,
∴∠BCE=∠FEC,∠EFC=∠GCF,
∴∠DCE=∠FEC,∠EFC=∠DCF,
∴OE=OC,OF=OC,
∴OE=OF;
(2)∵点O为CD的中点,
∴OD=OC,
又OE=OF,
∴四边形DECF是平行四边形,
∵CE平分∠BCD、CF平分∠GCD,
∴∠DCE=∠BCD,∠DCF=∠DCG
∴∠DCE+∠DCF=(∠BCD+∠DCG)=90°,
即∠ECF=90°,
∴四边形DECF是矩形.
17.(1)证明:∵AE∥BC,BE∥AC,
∴四边形AEDC是平行四边形.
∴AE=CD.
在△ABC中,AB=AC,AD为BC边上的高,
∴∠ADB=90°,BD=CD.
∴BD=AE.
∴四边形AEBD是矩形.
(2)解:在Rt△ADC中,∠ADB=90°,AC=5,BD=CD=BC=3,
∴AD==4.
∴四边形AEBD的面积=BD?AD═3×4=12.
18.(1)证明:∵E是AC的中点,
∴EC=AC,
∵DB=AC,
∴DB=AE,
又∵DB∥AC,
∴∠DBO=∠EAO,∠BDO=∠AEO,
在△AEO与△BDO中,
,
∴△AEO≌△BDO;
(2)△ABC满足AB=BC时,四边形DBEA是矩形.
理由如下:∵E是AC的中点,
∴AE=AC,
∵DB=AC,
∴DB=AE,
又∵DB∥AC,
∴四边形DBEA是平行四边形(一组对边平行且相等的四边形是平行四边形),
∵AB=BC,E为AC中点,
∴∠AEB=90°,
∴平行四边形DBEA是矩形,
即△ABC满足AB=BC时,四边形DBEA是矩形.
19.解:(1)当DE=CF时,四边形EFCD为矩形,
则有6﹣t=10﹣2t,解得t=4,
答:t=4s时,四边形EFCD为矩形.
(2)①当点F在线段BM上,AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,
则有t=4﹣2t,解得t=,
②当F在线段CM上,AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,
则有t=2t﹣4,解得t=4,
综上所述,t=4或s时,以A、M、E、F为顶点的四边形是平行四边形.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∵DF=BE,
∴四边形BFDE是平行四边形,
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)解:∵四边形BFDE是矩形,
∴∠BFD=90°,
∴∠BFC=90°,
在Rt△BCF中,CF=3,BF=4,
∴BC=5,
∵AF平分∠DAB,
∴∠DAF=∠BAF,
∵AB∥DC,
∴∠DFA=∠BAF,
∴∠DAF=∠DFA,
∴AD=DF,
∵AD=BC,
∴DF=BC,
∴DF=5.
21.(1)解:如图所示:
(2)证明:∵点E,F分别为OA,OB的中点,
∴EF∥AB,EF=AB,
同理:NM∥CD,MN=DC,
∵四边形ABCD是矩形,
∴AB∥DC,AB=DC,AC=BD,
∴EF∥NM,EF=MN,
∴四边形EFMN是平行四边形,
∵点E,F,M,N分别为OA,OB,OC,OD的中点,
∴EO=AO,MO=CO,
在矩形ABCD中,AO=CO=AC,BO=DO=BD,
∴EM=EO+MO=AC,
同理可证FN=BD,
∴EM=FN,
∴四边形EFMN是矩形.
(3)解:∵DM⊥AC于点M,
由(2)MO=CO,
∴DO=CD,
在矩形ABCD中,
AO=CO=AC,BO=DO=BD,AC=BD,
∴AO=BO=CO=DO,
∴△COD是等边三角形,
∴∠ODC=60°,
∵MN∥DC,
∴∠FNM=∠ODC=60°,
在矩形EFMN中,∠FMN=90°.
∴∠NFM=90°﹣∠FNM=30°,
∵NO=3,
∴FN=2NO=6,FM=3,MN=3,
∵点F,M分别为OB,OC的中点,
∴BC=2FM=6,
∴矩形的面积为BC?CD=36.
能力达标专题提升训练(附答案)
一.选择题
1.如图,矩形ABCD中,点G是AD的中点,GE⊥BG交CD于点E,CB=CE,连接CG交BE于点F,则∠ECF的度数为( )
A.30°
B.22.5°
C.25°
D.15°
2.如图,在矩形ABCD中,E是AB的中点,动点F从点B出发,沿BC运动到点C时停止,以EF为边作?EFGH,且点G、H分别在CD、AD上.在动点F运动的过程中,?EFGH的面积( )
A.逐渐增大
B.逐渐减小
C.不变
D.先增大,再减小
3.已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥BD于点E,PF⊥AC于点F,则PE+PF等于( )
A.
B.
C.
D.
4.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=( )
A.60°
B.45°
C.30°
D.22.5°
5.如图,四边形ABCD中,E,F分别是边AD,BC的中点,G,H分别是对角线BD,AC的中点,若四边形EGFH为矩形,则四边形ABCD需满足的条件是( )
A.AC=BD
B.AC⊥BD
C.AB=DC
D.AB⊥DC
6.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )
A.1.2
B.1.25
C.2.4
D.2.5
7.如图,在矩形ABCD中,AB=6,BC=8,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE的长是( )
A.1
B.
C.2
D.
二.填空题
8.如图,矩形ABCD中,M是边CD的中点,连接AM,取AM的中点N,连接BN.若AB=2,BC=3,则BN的长为
.
9.如图,矩形ABCD中,AB=3,BC=4,DE平分∠ADC交BC于点E,AF平分∠BAD交BC于点F,交DE于点G,则=
.
10.如图,长方形ABCD中,AD=20,AB=8,点Q是BC的中点,点P在AD边上运动,当△BPQ是等腰三角形时,AP的长为
.
11.如图,F是矩形ABCD内一点,AF=BF,连接DF并延长交BC于点G,且点C与AB的中点E恰好关于直线DG对称,若AD=6,则AB的长为
.
12.如图,矩形ABCD的对角线AC与BD交于点O,点E在AD上,且DE=CD,连接OE,BE,AC与BE相交于点F,∠ABE=∠ACB,则下列结论:①BE=DE;②OE⊥BD;③△AEF是等腰三角形;④当AE=2,则OE的长为,其中正确的结论是
.(填写所有正确结论的序号)
13.如图,M为矩形ABCD中AD边中点,E、F分别为BC、CD上的动点,且BE=2DF,若AB=1,BC=2,则ME+2AF的最小值为
.
三.解答题
14.如图,在矩形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.过点C作CF∥BD交线段OE的延长线于点F,连接DF.
求证:(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
15.如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
16.已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于点O.
(1)求证:OE=OF;
(2)若点O为CD的中点,求证:四边形DECF是矩形.
17.如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连接BE.
(1)求证:四边形AEBD是矩形;
(2)求四边形AEBD的面积.
18.如图,DB∥AC,且DB=AC,E是AC的中点.
(1)求证:△AEO≌△BDO;
(2)连接AD、BE,探究:当△ABC满足什么条件时,四边形DBEA是矩形?并证明你的结论.
19.在四边形ABCD中,AD∥BC,BC⊥CD,AD=6cm,BC=10cm,点E从A出发以1cm/s的速度向D运动,点F从点B出发,以2cm/s的速度向点C运动,当其中一点到达终点,而另一点也随之停止,设运动时间为t,
(1)t取何值时,四边形EFCD为矩形?
(2)M是BC上一点,且BM=4,t取何值时,以A、M、E、F为顶点的四边形是平行四边形?
20.如图,在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠DAB,CF=3,BF=4,求DF长.
21.如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.
(1)依题意,补全图形;
(2)求证:四边形EFMN是矩形;
(3)连接DM,若DM⊥AC于点M,ON=3,求矩形ABCD的面积.
参考答案
一.选择题
1.解:取BE的中点O,连接OG,OC,
∵O,G为中点,
∴OG为四边形ADEB的中位线,
∴AB∥OG∥DE,
∴∠OGC=∠ECF,
∵CE=BC,∠BCE=90°,
∴△BCE是等腰直角三角形,
∴∠CBE=∠BEC=45°,
∵∠BCE=90°,O为BE的中点,
∴OC=OE=BE,
∴∠OCE=∠OEC=45°,
∵GE⊥BG,O为BE的中点,
∴OG=BE,
∴OG=OC,
∴∠OGC=∠OCG,
∴∠OCG=∠ECF=∠OCE=22.5°,
故选:B.
2.解:设AB=a,BC=b,BE=c,BF=x,
连接EG,
∵四边形EFGH为平行四边形,
∴EF=HG,EF∥HG,
∴∠FEG=∠HGE,
∵四边形ABCD为矩形,
∴AB∥CD,
∴∠BEG=∠DGE,
∴∠BEG﹣∠FEG=∠DGE﹣∠EGH,
∴∠BEF=∠HGD
∵EF=HG,∠B=∠D,
∴Rt△BEF≌Rt△DGH(AAS),
同理Rt△AEH≌Rt△GFC,
∴S平行四边形EFGH=S矩形ABCD﹣2(S△BEF+S△AEH)
=ab﹣2[cx+(a﹣c)(b﹣x)]
=ab﹣(cx+ab﹣ax﹣bc+cx)
=ab﹣cx﹣ab+ax+bc﹣cx
=(a﹣2c)x+bc,
∵E是AB的中点,
∴a=2c,
∴a﹣2c=0,
∴S平行四边形EFGH=bc=ab,
故选:C.
3.解:连接PO,
∵矩形ABCD的两边AB=5,BC=12,
∴S矩形ABCD=AB?BC=60,OA=OC,OB=OD,AC=BD,AC===13,
∴S△AOD=S矩形ABCD=15,OA=OD=AC=,
∴S△AOD=S△AOP+S△DOP=OA?PE+OD?PF=OA(PE+PF)=××(PE+PF)=15,
∴PE+PF=,
故选:C.
4.解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC,OB=OD,
∴OA=OB═OC,
∴∠OAD=∠ODA,∠OAB=∠OBA,
∴∠AOE=∠OAD+∠ODA=2∠OAD,
∵∠EAC=2∠CAD,
∴∠EAO=∠AOE,
∵AE⊥BD,
∴∠AEO=90°,
∴∠AOE=45°,
∴∠OAB=∠OBA=(180°﹣45°)=67.5°,
∴∠BAE=∠OAB﹣∠OAE=22.5°.
故选:D.
5.解:若四边形EGFH为矩形,则四边形ABCD需满足的条件是AB⊥DC,理由如下:
∵E,G分别是AD,BD的中点,
∴EG是△DAB的中位线,
∴EG=AB,EG∥AB,
同理,FH=AB,FH∥AB,GF∥DC,
∴EG=FH,EG∥FH,
∴四边形EGFH是平行四边形,
∵AB⊥DC,GF∥DC,FH∥AB,
∴GF⊥FH,
∴∠GFH=90°,
∴平行四边形EGFH是矩形,
故选:D.
6.解:连接AP,如图:
∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=90°,
∵∠BAC=90°,
∴四边形AFPE是矩形,
∴EF=AP,
要使EF最小,只要AP最小即可,
当AP⊥BC时,AP最短,
∵∠BAC=90°,AB=3,AC=4,
∴BC===5,
∵△ABC的面积=×4×3=×5×AP,
∴AP=2.4,
即EF=2.4,
故选:C.
7.解:连接CE,如图所示:
∵四边形ABCD是矩形,
∴∠ADC=90°,CD=AB=6,AD=BC=8,OA=OC,
∵EF⊥AC,
∴AE=CE,
设DE=x,则CE=AE=8﹣x,
在Rt△CDE中,由勾股定理得:x2+62=(8﹣x)2,
解得:x=,
即DE=;
故选:B.
二.填空题
8.解:过点N作GH∥AB,分别交BC于点G,交AD于点H,如图,
∵矩形ABCD,
∴AB=CD,AD=BC,∠C=∠ABG=90°,AB∥CD,
∴四边形CDHG,四边形GHAB为矩形,
∴∠BGN=90°,GH=CD=AB,GH∥CD∥AB,
∵N为AM中点,
∴MN=AN,DH=HA,
∴CG=GB=BC=,H为DA的中点,
∴NH为△AMD的中位线,
∴NH=MD,
∵M是CD的中点,
∴MD=CD=AB=1,
∴NH=,
∴GN=GH﹣NH=AB﹣NH=,
在Rt△BGN中,由勾股定理得,
BN==,
故答案为:.
9.解:如图,过点G作AD的垂线,分别交AD,BC于点N,M,
则四边形CDNM是矩形,
∴MN=CD=AB=3,CM=DN,
∵四边形ABCD是矩形,
∴AD∥BC,BC=AD=4,
∵DE平分∠ADC交BC于点E,AF平分∠BAD交BC于点F,
∴∠DAG=∠ADG=∠GEF=∠GFE=45°,
∴△AGD和△GEF均为等腰直角三角形,
∴GN=DN=AD=2,
∴GM=MN﹣GN=AB﹣GN=3﹣2=1,
MC=DN=2,
∴MF=GM=1,
∴CG===,
∴GF=,
∴==.
故答案为:.
10.解:∵四边形ABCD为矩形,AD=20,
∴BQ=10,
①当BP=PQ时,过P作PM⊥BQ,交BQ于点M,如图1所示:
则BM=MQ=5,且四边形ABMP为矩形,
∴AP=BM=5,
②当BQ=BP时,则BP=10,在Rt△ABP中,AB=8,由勾股定理可求得AP=6,
③当PQ=BQ时,
过Q作QN⊥RS,交RS于点N,则可知RN=SN,
在Rt△RNQ中,可求得RN=SN=6,
则AR=4,AS=16,
即R、S为满足条件的P点的位置,
∴AP=4或16,
综上可知AP为4或5或6或16,
故答案为:4或5或6或16.
11.解:连接EF、EG、EC,如图所示:
∵四边形ABCD是矩形,
∴BC=AD=6,AD∥BC,∠BAD=∠ABC=90°,
∴AB⊥AD,
∵AF=BF,点E是AB的中点,
∴EF⊥AB,AB=2BE,AE=BE,
∴∠AEF=∠ABC=90°,
∴EF∥BC,
∴EF∥AD∥BC,
∴DF=FG,
在Rt△DCG中,CF为斜边DG上的中线,
∴CF=DG=FG,
∵EF∥GC,
∴∠OEF=∠OCG,∠OFE=∠OGC,
∵点C与AB的中点E关于直线DG对称,
∴DG垂直平分线段EC,
∴FG⊥CE,EO=CO,EF=CF,
在△OEF和△OCG中,
,
∴△OEF≌△OCG(AAS),
∴EF=CG,
∴CF=FG=CG,
∴△CGF是等边三角形,
∴∠GCF=60°,
∵CO⊥GF,
∴CO平分∠GCF,
∴∠GCO=GCF=30°,
在Rt△BCE中,∠EBC=90°,∠BCE=30°,BC=6,
∴CE=2BE,
∴BE===2.
∴AB=2BE=4;
故答案为:4.
12.解:∵四边形ABCD是矩形,
∴AB=CD,∠BAE=90°,
∵DE=CD,
∴AB=DE,
∵AB<BE,
∴BE≠DE,故①错误;
∵BO=DO,BE≠DE,
∴OE与BD不垂直,故②错误;
如图,作CH⊥BE于H,EG⊥BD于G.设BE与AC的交点为F.
则∠HBC+∠BCH=∠BHC=90°,
∵四边形ABCD为矩形,
∴AD=BC,AB=CD,∠ABC=∠BAD=90°,AD∥BC,AC=BD
∴∠ABE+∠CBH=90°,
∴∠ABE=∠BCH,
∵∠ABE=∠ACB,
∴∠BCH=∠GCH,
∴BH=FH,BC=CG,∠CBH=∠CGH,
设AB=x,则ED=CD=AB=x,
∵AE=2,所以AD=AE+ED=2+x,
∴CB=CF=2+x,
∵AD∥BC,
∴∠AEG=∠CBH=∠CGH=∠AGE,
∴AF=AE=2,故③正确;
∴AC=AG+CG=4+x,
在Rt△ABC中:AB2+BC2=AC2,
∴x2+(x+2)2=(x+4)2,解得x1=6,x2=﹣2(舍),
∴AB=CD=6,AD=AC=8,AC=BD=10,
∵AC与BD交于点O,
∴AO=BO=CO=DO=5,
∴EG=ED=,DG=ED=,
∴OG=OD﹣DG=5﹣=,
在Rt△OGE中:
OE2=EG2+OG2=()2+()2==13,
∴OE=,故④正确.
故其中正确的结论是③④.
故答案为:③④.
13.解:如图,过点M作MH⊥BC于H.设DF=x,则BE=2x.
∵四边形ABCD是矩形,
∴∠BAD=∠B=∠D=90°,
∵MH⊥BC,
∴∠MHB=90°,
∴四边形ABHM是矩形,
∴AM=DM=BH=1,AB=MH=1,
∴EH=1﹣2x,
∴ME+2AF=+2=+,
欲求ME+2AF的最小值,相当于在x轴上找一点Q(2x,0),使得点Q到J(0,4),和K(1,1)的距离之和最小(如下图),
作点J关于x轴的对称点J′,连接KJ′交x轴于Q,连接JQ,此时JQ+QK的值最小,最小值=KJ′,
∵J′(0,﹣4),K(1,1),
∴KJ′==,
∴ME+2AF的最小值为,
故答案为.
三.解答题
14.证明:(1)∵CF∥BD,
∴∠ODE=∠FCE,
∵E是CD中点,
∴CE=DE,
在△ODE和△FCE中,
,
∴△ODE≌△FCE(ASA);
(2)∵△ODE≌△FCE,
∴OD=FC,
∵CF∥BD,
∴四边形ODFC是平行四边形,
在矩形ABCD中,OC=OD,
∴四边形ODFC是菱形.
15.(1)证明:∵四边形ABCD是矩形,
∴AB=DC,∠A=∠D=90°,
∵M为AD中点,
∴AM=DM,
在△ABM和△DCM,
,
∴△ABM≌△DCM(SAS);
(2)四边形MENF是菱形.
证明如下:∵N、E、F分别是BC、BM、CM的中点,
∴NE∥CM,NE=CM,MF=CM,
∴NE=FM,NE∥FM,
∴四边形MENF是平行四边形,
由(1)知△ABM≌△DCM,
∴BM=CM,
∵E、F分别是BM、CM的中点,
∴ME=MF,
∴平行四边形MENF是菱形;
16.证明:
(1)∵CE平分∠BCD、CF平分∠GCD,
∴∠BCE=∠DCE,∠DCF=∠GCF,
∵EF∥BC,
∴∠BCE=∠FEC,∠EFC=∠GCF,
∴∠DCE=∠FEC,∠EFC=∠DCF,
∴OE=OC,OF=OC,
∴OE=OF;
(2)∵点O为CD的中点,
∴OD=OC,
又OE=OF,
∴四边形DECF是平行四边形,
∵CE平分∠BCD、CF平分∠GCD,
∴∠DCE=∠BCD,∠DCF=∠DCG
∴∠DCE+∠DCF=(∠BCD+∠DCG)=90°,
即∠ECF=90°,
∴四边形DECF是矩形.
17.(1)证明:∵AE∥BC,BE∥AC,
∴四边形AEDC是平行四边形.
∴AE=CD.
在△ABC中,AB=AC,AD为BC边上的高,
∴∠ADB=90°,BD=CD.
∴BD=AE.
∴四边形AEBD是矩形.
(2)解:在Rt△ADC中,∠ADB=90°,AC=5,BD=CD=BC=3,
∴AD==4.
∴四边形AEBD的面积=BD?AD═3×4=12.
18.(1)证明:∵E是AC的中点,
∴EC=AC,
∵DB=AC,
∴DB=AE,
又∵DB∥AC,
∴∠DBO=∠EAO,∠BDO=∠AEO,
在△AEO与△BDO中,
,
∴△AEO≌△BDO;
(2)△ABC满足AB=BC时,四边形DBEA是矩形.
理由如下:∵E是AC的中点,
∴AE=AC,
∵DB=AC,
∴DB=AE,
又∵DB∥AC,
∴四边形DBEA是平行四边形(一组对边平行且相等的四边形是平行四边形),
∵AB=BC,E为AC中点,
∴∠AEB=90°,
∴平行四边形DBEA是矩形,
即△ABC满足AB=BC时,四边形DBEA是矩形.
19.解:(1)当DE=CF时,四边形EFCD为矩形,
则有6﹣t=10﹣2t,解得t=4,
答:t=4s时,四边形EFCD为矩形.
(2)①当点F在线段BM上,AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,
则有t=4﹣2t,解得t=,
②当F在线段CM上,AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,
则有t=2t﹣4,解得t=4,
综上所述,t=4或s时,以A、M、E、F为顶点的四边形是平行四边形.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∵DF=BE,
∴四边形BFDE是平行四边形,
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)解:∵四边形BFDE是矩形,
∴∠BFD=90°,
∴∠BFC=90°,
在Rt△BCF中,CF=3,BF=4,
∴BC=5,
∵AF平分∠DAB,
∴∠DAF=∠BAF,
∵AB∥DC,
∴∠DFA=∠BAF,
∴∠DAF=∠DFA,
∴AD=DF,
∵AD=BC,
∴DF=BC,
∴DF=5.
21.(1)解:如图所示:
(2)证明:∵点E,F分别为OA,OB的中点,
∴EF∥AB,EF=AB,
同理:NM∥CD,MN=DC,
∵四边形ABCD是矩形,
∴AB∥DC,AB=DC,AC=BD,
∴EF∥NM,EF=MN,
∴四边形EFMN是平行四边形,
∵点E,F,M,N分别为OA,OB,OC,OD的中点,
∴EO=AO,MO=CO,
在矩形ABCD中,AO=CO=AC,BO=DO=BD,
∴EM=EO+MO=AC,
同理可证FN=BD,
∴EM=FN,
∴四边形EFMN是矩形.
(3)解:∵DM⊥AC于点M,
由(2)MO=CO,
∴DO=CD,
在矩形ABCD中,
AO=CO=AC,BO=DO=BD,AC=BD,
∴AO=BO=CO=DO,
∴△COD是等边三角形,
∴∠ODC=60°,
∵MN∥DC,
∴∠FNM=∠ODC=60°,
在矩形EFMN中,∠FMN=90°.
∴∠NFM=90°﹣∠FNM=30°,
∵NO=3,
∴FN=2NO=6,FM=3,MN=3,
∵点F,M分别为OB,OC的中点,
∴BC=2FM=6,
∴矩形的面积为BC?CD=36.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
