2.3等差数列的前n项和(1)
文档属性
| 名称 | 2.3等差数列的前n项和(1) |

|
|
| 格式 | zip | ||
| 文件大小 | 649.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-26 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
课前复习
(3)等差中项.
(1)等差数列的定义.
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列
(2)等差数列通项公式
若a、b、c成等差数列,则2b=a+c
(推广)若m、n、p、q∈N*且m+n=p+q,则am+an=ap+aq
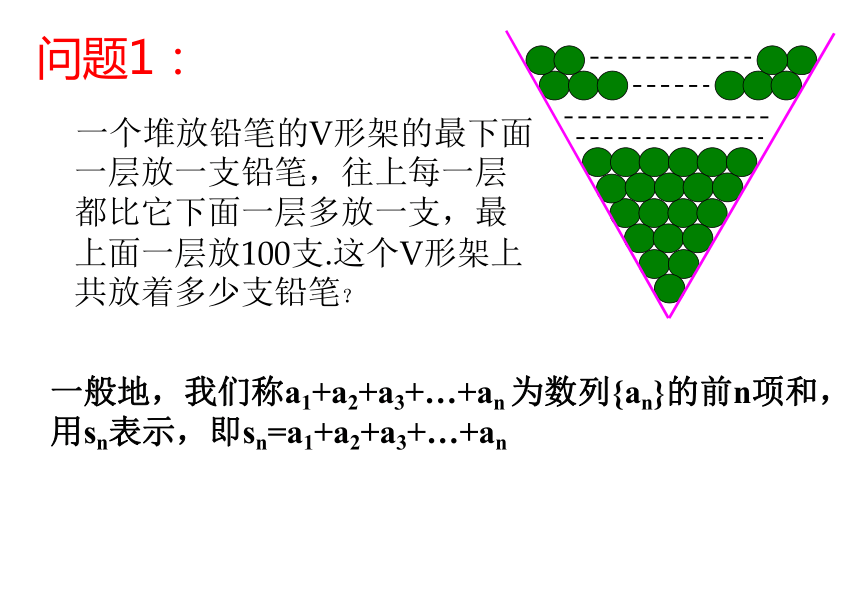
问题1:
一个堆放铅笔的V形架的最下面一层放一支铅笔,往上每一层都比它下面一层多放一支,最上面一层放100支.这个V形架上共放着多少支铅笔?
一般地,我们称a1+a2+a3+…+an 为数列{an}的前n项和,
用sn表示,即sn=a1+a2+a3+…+an
§2.3等差数列前n项和
在高斯10岁的时候,他的老师出了一道数学题:
1+2+3+…+98+99+100=?
在别的同学都在忙着计算的时候,高斯很快得出了正确答案,你知道高斯是怎 么计算的吗?
高斯(Gauss,C.F.,1777年~1855年)
德国著名数学家
著名数学家高斯的一个小故事
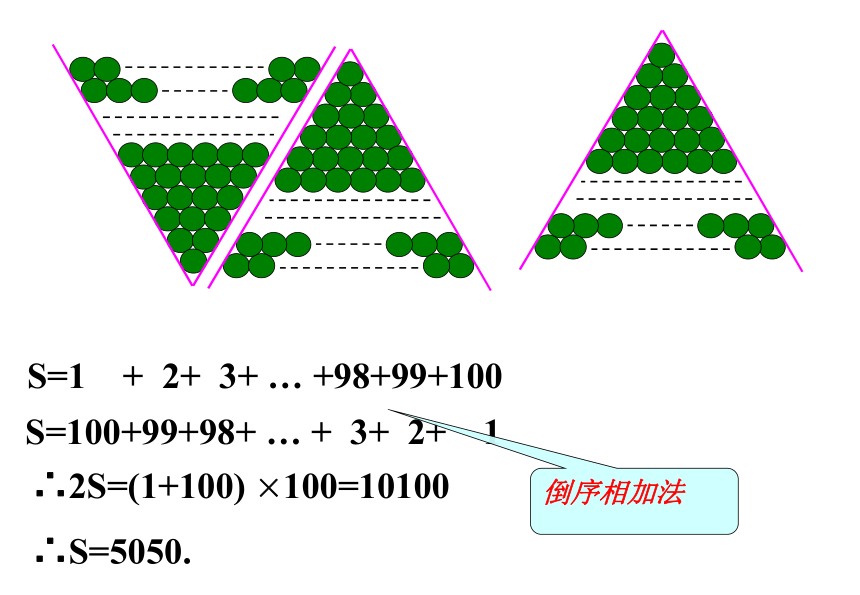
S=1 + 2+ 3+ … +98+99+100
S=100+99+98+ … + 3+ 2+ 1
∴2S=(1+100) ×100=10100
∴S=5050.
倒序相加法
问题3:设等差数列 {an} 的首项为a1, 公差为d,如何求等差数列的前n项和
Sn= a1 +a2+a3+…+an=
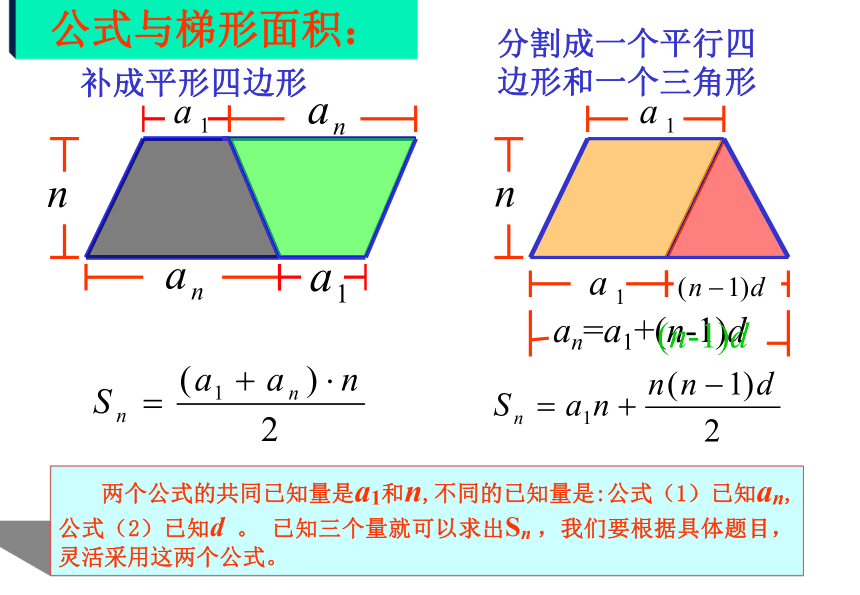
公式与梯形面积:
补成平形四边形
分割成一个平行四边形和一个三角形
两个公式的共同已知量是a1和n,不同的已知量是:公式(1)已知an,公式(2)已知d 。 已知三个量就可以求出Sn ,我们要根据具体题目,灵活采用这两个公式。
an=a1+(n-1)d
(n-1)d
求和
例1 :
(1)-10,-6,-2, 2, ···, (4n-14)
注意在运用公式时,
要看清等差数列的项数。
公式的应用一
例
题
解
析
变式:等差数列-10,-6,-2,2,·······前多少项和是54 ?
在等差数列的求和公式中,含有四个量,运用方程的思想,知三可求一.
例2:等差数列{an}的首项为a1,公差为d,项数为n,第n项为an,前n项和为Sn,请填写下表:
a1 d n an sn
5 10 10
-2 50 2550
-38 -10 -360
14.5 26 32
95
500
100
2
15
2
0.7
604.5
Sn,a1 ,an,n,d
知三求二
随堂练习
1、根据下列各题中的条件,求相应的等差数列{an}的前n项和Sn
(1)a1=5, an=95, n=10
(2)a1=100, d=-2, n=50
(3)a1=14.5, d=0.7, an=32
知三求二
之
例3 2000年11月14日教育部下发了《关于在中小学实施“校校通”工程的通知》。某市据此提出了实施“校校通”工程的总目标:从2001年起用10年的时间,在全市中小学建成不同标准的校园网。据测算,2001年该市用于“校校通”工程的经费为500万元。为了保证工程的顺利实施,计划每年投入的资金都比上一年增加50万元。那么从2001年起的未来10年内,该市在“校校通”工程中的总投入是多少?
解:由题意,从2001~2010年,该市每年投入“校校通”工程的经费都比上一年增加50万元。所以,可建立一个等差数列{an},表示从2001年起各年投入的资金,其中
a1=500, d=50,
n=10
投入资金总额为:
答:从2001~2010年,该市每年投入“校校通”的总资金为7250万元。
公式的应用二
小结:
1.公式的推导方法:倒序相加法。
3.公式的应用。
2.等差数列前n项和公式。
在公式中有 a1, an, n, d, sn五个量,
已知其中三个可以求出另外两个。
作业:
作业本22页
课后思考题
课前复习
(3)等差中项.
(1)等差数列的定义.
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列
(2)等差数列通项公式
若a、b、c成等差数列,则2b=a+c
(推广)若m、n、p、q∈N*且m+n=p+q,则am+an=ap+aq
问题1:
一个堆放铅笔的V形架的最下面一层放一支铅笔,往上每一层都比它下面一层多放一支,最上面一层放100支.这个V形架上共放着多少支铅笔?
一般地,我们称a1+a2+a3+…+an 为数列{an}的前n项和,
用sn表示,即sn=a1+a2+a3+…+an
§2.3等差数列前n项和
在高斯10岁的时候,他的老师出了一道数学题:
1+2+3+…+98+99+100=?
在别的同学都在忙着计算的时候,高斯很快得出了正确答案,你知道高斯是怎 么计算的吗?
高斯(Gauss,C.F.,1777年~1855年)
德国著名数学家
著名数学家高斯的一个小故事
S=1 + 2+ 3+ … +98+99+100
S=100+99+98+ … + 3+ 2+ 1
∴2S=(1+100) ×100=10100
∴S=5050.
倒序相加法
问题3:设等差数列 {an} 的首项为a1, 公差为d,如何求等差数列的前n项和
Sn= a1 +a2+a3+…+an=
公式与梯形面积:
补成平形四边形
分割成一个平行四边形和一个三角形
两个公式的共同已知量是a1和n,不同的已知量是:公式(1)已知an,公式(2)已知d 。 已知三个量就可以求出Sn ,我们要根据具体题目,灵活采用这两个公式。
an=a1+(n-1)d
(n-1)d
求和
例1 :
(1)-10,-6,-2, 2, ···, (4n-14)
注意在运用公式时,
要看清等差数列的项数。
公式的应用一
例
题
解
析
变式:等差数列-10,-6,-2,2,·······前多少项和是54 ?
在等差数列的求和公式中,含有四个量,运用方程的思想,知三可求一.
例2:等差数列{an}的首项为a1,公差为d,项数为n,第n项为an,前n项和为Sn,请填写下表:
a1 d n an sn
5 10 10
-2 50 2550
-38 -10 -360
14.5 26 32
95
500
100
2
15
2
0.7
604.5
Sn,a1 ,an,n,d
知三求二
随堂练习
1、根据下列各题中的条件,求相应的等差数列{an}的前n项和Sn
(1)a1=5, an=95, n=10
(2)a1=100, d=-2, n=50
(3)a1=14.5, d=0.7, an=32
知三求二
之
例3 2000年11月14日教育部下发了《关于在中小学实施“校校通”工程的通知》。某市据此提出了实施“校校通”工程的总目标:从2001年起用10年的时间,在全市中小学建成不同标准的校园网。据测算,2001年该市用于“校校通”工程的经费为500万元。为了保证工程的顺利实施,计划每年投入的资金都比上一年增加50万元。那么从2001年起的未来10年内,该市在“校校通”工程中的总投入是多少?
解:由题意,从2001~2010年,该市每年投入“校校通”工程的经费都比上一年增加50万元。所以,可建立一个等差数列{an},表示从2001年起各年投入的资金,其中
a1=500, d=50,
n=10
投入资金总额为:
答:从2001~2010年,该市每年投入“校校通”的总资金为7250万元。
公式的应用二
小结:
1.公式的推导方法:倒序相加法。
3.公式的应用。
2.等差数列前n项和公式。
在公式中有 a1, an, n, d, sn五个量,
已知其中三个可以求出另外两个。
作业:
作业本22页
课后思考题
