5.3.1函数的单调性 教案——2020-2021学年高二下学期数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 5.3.1函数的单调性 教案——2020-2021学年高二下学期数学人教A版(2019)选择性必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 19.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-02 00:00:00 | ||
图片预览

文档简介
第五章
一元函数的导数及其应用
5.3
导数在研究函数中的应用
5.3.1
函数的单调性
教学设计
一、教学目标
1.
理解可导函数的单调性与其导数的关系;
2.
能够利用导数确定函数的单调性以及函数的单调区间;
3.
能够利用函数的单调性解决有关问题.
二、教学重难点
1.
教学重点
利用导数确定函数的单调性以及函数的单调区间.
2.
教学难点
证明不等式及逆向求参问题.
三、教学过程
(一)新课导入
问题1
如图(1)是某高台跳水运动员的重心相对于水面的高度h随时间t变化的函数的图象,图(2)是跳水运动员的速度v随时间t变化的函数的图象.,b是函数的零点.运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?如何从数学上刻画这种区别?
(二)探索新知
观察图象可以发现:
(1)从起跳到最高点,运动员的重心处于上升状态,离水面的高度h随时间t的增加而增加,即单调递增.相应地,.
(2)从最高点到入水,运功员的重心处于下降状态,画水面的高度h随时间t的增加而减小,即单调递减.相应地,.
思考:从以上观察中发现,函数的单调性与的正负有内在联系.那么,我们能否由的正负来判断函数的单调性呢?
在问题1中,可以发现:
当时,,函数的图象是“上升”的,函数在上单调递增;
当时,,函数的图象是“下降”的,函数在上单调递减.
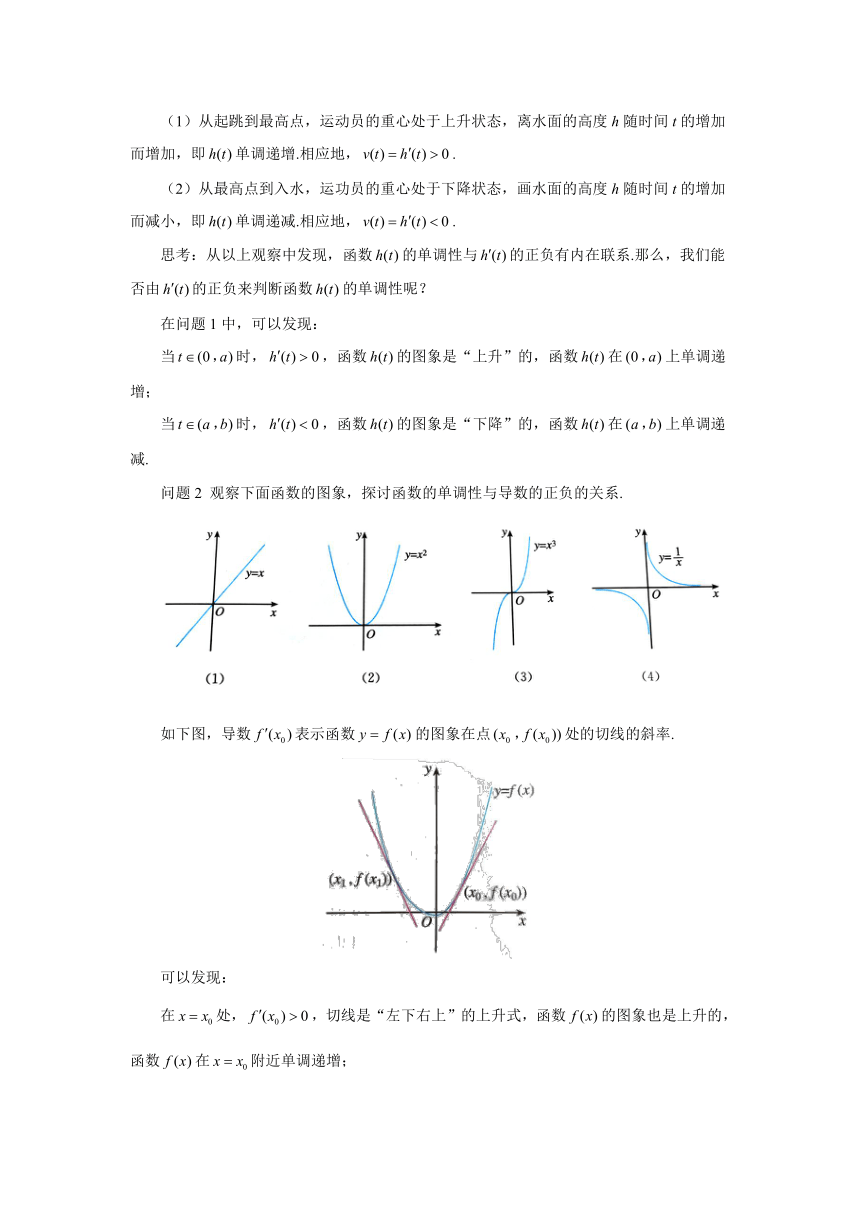
问题2
观察下面函数的图象,探讨函数的单调性与导数的正负的关系.
如下图,导数表示函数的图象在点处的切线的斜率.
可以发现:
在处,,切线是“左下右上”的上升式,函数的图象也是上升的,函数在附近单调递增;
在处,,切线是“左上右下”的下降式,函数的图象也是下降的,函数在附近单调递减.
结论:一般地,函数的单调性与导函数的正负之间具有如下的关系:
在某个区间上,如果,那么函数在区间上单调递增;
在某个区间上,如果,那么函数在区间上单调递减.
例1
利用导数判断下列函数的单调性:
(1);(2);(3).
解:(1)因为,所以.
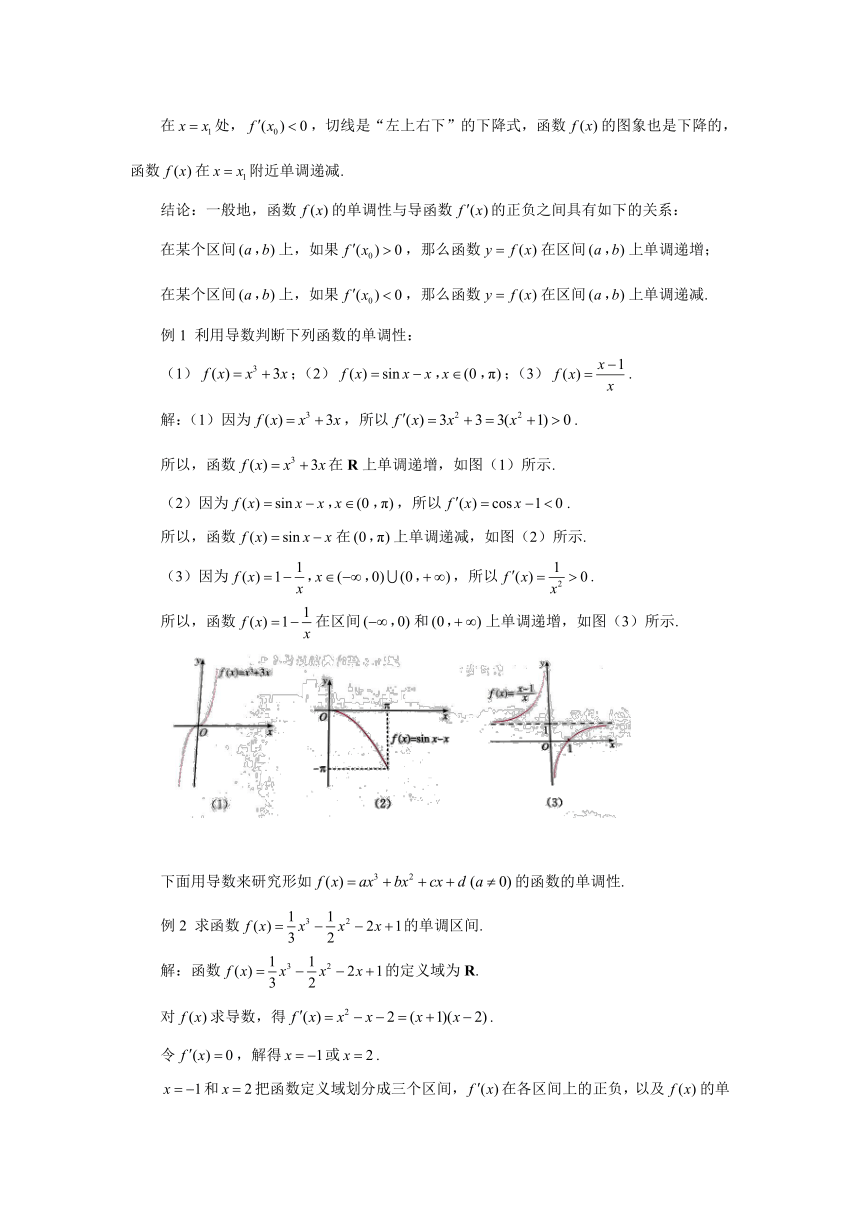
所以,函数在R上单调递增,如图(1)所示.
(2)因为,所以.
所以,函数在上单调递减,如图(2)所示.
(3)因为,所以.
所以,函数在区间和上单调递增,如图(3)所示.
下面用导数来研究形如的函数的单调性.
例2
求函数的单调区间.
解:函数的定义域为R.
对求导数,得.
令,解得或.
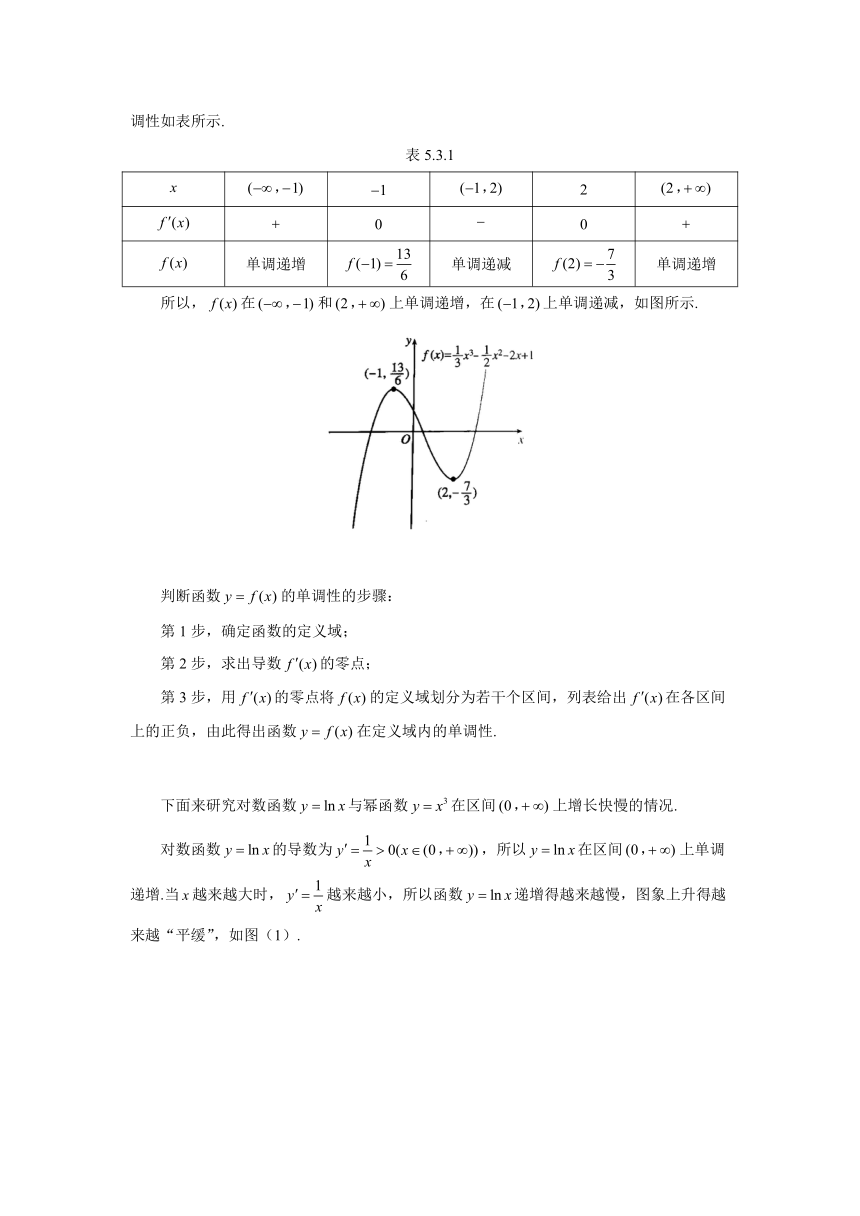
和把函数定义域划分成三个区间,在各区间上的正负,以及的单调性如表所示.
表5.3.1
2
0
0
单调递增
单调递减
单调递增
所以,在和上单调递增,在上单调递减,如图所示.
判断函数的单调性的步骤:
第1步,确定函数的定义域;
第2步,求出导数的零点;
第3步,用的零点将的定义域划分为若干个区间,列表给出在各区间上的正负,由此得出函数在定义域内的单调性.
下面来研究对数函数与幂函数在区间上增长快慢的情况.
对数函数的导数为,所以在区间上单调递增.当越来越大时,越来越小,所以函数递增得越来越慢,图象上升得越来越“平缓”,如图(1).
幂函数的导数为,所以在区间上单调递增.
当越来越大时,越来越大,函数递增得越来越快,图象上升得越来越“陡峭”,如图(2).
一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得较快,这时函数的图象就比较“陡峭”(向上或向下);反之,函数在这个范围内变化得较慢,函数的图象就比较“平缓”.
例3
设,两个函数的图象如图所示.判断,的图象与,之间的对应关系.
解:因为,所以.
当时,;
当时,;
当时,.
所以,,在上都是增函数.在区间上,的图象比的图象要“陡峭”;在区间上,的图象比的图象要“平缓”.
所以,,的图象依次是图中的,.
(三)课堂练习
1.下列函数中,在上为增函数的是(
)
A.
B.
C.
D.
答案:B
解析:B中,在上恒成立,在上为增函数.对于选项A,C,D,都存在,使的情况.故选B.
2.函数的单调递减区间为(
)
A.
B.
C.
D.
答案:C
解析:由题可得,令,即,解得或,又因为,所以.故选C.
3.若函数在区间上单调递增,则实数的取值范围是(
)
A.
B.
C.
D.
答案:C
解析:,.
函数在区间上单调递增,
,即,得.
当时,,
实数的取值范围是.故选C.
4.已知函数,则的单调递增区间为_________________.
答案:
解析:因为,,
所以.
由可得,所以或,
即的单调递增区间为.
5.已知,函数.
(1)若曲线在点处的切线与直线垂直,求的值;
(2)若函数在区间上单调递减,求的取值范围.
答案:(1)因为,
所以曲线在点处的切线斜率.
而直线的斜率为,则,得.
(2)由在上单调递减,
得在上恒成立,
即在上恒成立.
又时,,所以,
所以的取值范围是.
小结作业
小结:利用导数确定函数的单调性以及函数的单调区间.
作业:
四、板书设计
5.3.1
函数的单调性
1.
函数的单调性与导数的关系;
2.
形如的函数的单调性.
3.
函数的变化快慢与导数的关系.
一元函数的导数及其应用
5.3
导数在研究函数中的应用
5.3.1
函数的单调性
教学设计
一、教学目标
1.
理解可导函数的单调性与其导数的关系;
2.
能够利用导数确定函数的单调性以及函数的单调区间;
3.
能够利用函数的单调性解决有关问题.
二、教学重难点
1.
教学重点
利用导数确定函数的单调性以及函数的单调区间.
2.
教学难点
证明不等式及逆向求参问题.
三、教学过程
(一)新课导入
问题1
如图(1)是某高台跳水运动员的重心相对于水面的高度h随时间t变化的函数的图象,图(2)是跳水运动员的速度v随时间t变化的函数的图象.,b是函数的零点.运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?如何从数学上刻画这种区别?
(二)探索新知
观察图象可以发现:
(1)从起跳到最高点,运动员的重心处于上升状态,离水面的高度h随时间t的增加而增加,即单调递增.相应地,.
(2)从最高点到入水,运功员的重心处于下降状态,画水面的高度h随时间t的增加而减小,即单调递减.相应地,.
思考:从以上观察中发现,函数的单调性与的正负有内在联系.那么,我们能否由的正负来判断函数的单调性呢?
在问题1中,可以发现:
当时,,函数的图象是“上升”的,函数在上单调递增;
当时,,函数的图象是“下降”的,函数在上单调递减.
问题2
观察下面函数的图象,探讨函数的单调性与导数的正负的关系.
如下图,导数表示函数的图象在点处的切线的斜率.
可以发现:
在处,,切线是“左下右上”的上升式,函数的图象也是上升的,函数在附近单调递增;
在处,,切线是“左上右下”的下降式,函数的图象也是下降的,函数在附近单调递减.
结论:一般地,函数的单调性与导函数的正负之间具有如下的关系:
在某个区间上,如果,那么函数在区间上单调递增;
在某个区间上,如果,那么函数在区间上单调递减.
例1
利用导数判断下列函数的单调性:
(1);(2);(3).
解:(1)因为,所以.
所以,函数在R上单调递增,如图(1)所示.
(2)因为,所以.
所以,函数在上单调递减,如图(2)所示.
(3)因为,所以.
所以,函数在区间和上单调递增,如图(3)所示.
下面用导数来研究形如的函数的单调性.
例2
求函数的单调区间.
解:函数的定义域为R.
对求导数,得.
令,解得或.
和把函数定义域划分成三个区间,在各区间上的正负,以及的单调性如表所示.
表5.3.1
2
0
0
单调递增
单调递减
单调递增
所以,在和上单调递增,在上单调递减,如图所示.
判断函数的单调性的步骤:
第1步,确定函数的定义域;
第2步,求出导数的零点;
第3步,用的零点将的定义域划分为若干个区间,列表给出在各区间上的正负,由此得出函数在定义域内的单调性.
下面来研究对数函数与幂函数在区间上增长快慢的情况.
对数函数的导数为,所以在区间上单调递增.当越来越大时,越来越小,所以函数递增得越来越慢,图象上升得越来越“平缓”,如图(1).
幂函数的导数为,所以在区间上单调递增.
当越来越大时,越来越大,函数递增得越来越快,图象上升得越来越“陡峭”,如图(2).
一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得较快,这时函数的图象就比较“陡峭”(向上或向下);反之,函数在这个范围内变化得较慢,函数的图象就比较“平缓”.
例3
设,两个函数的图象如图所示.判断,的图象与,之间的对应关系.
解:因为,所以.
当时,;
当时,;
当时,.
所以,,在上都是增函数.在区间上,的图象比的图象要“陡峭”;在区间上,的图象比的图象要“平缓”.
所以,,的图象依次是图中的,.
(三)课堂练习
1.下列函数中,在上为增函数的是(
)
A.
B.
C.
D.
答案:B
解析:B中,在上恒成立,在上为增函数.对于选项A,C,D,都存在,使的情况.故选B.
2.函数的单调递减区间为(
)
A.
B.
C.
D.
答案:C
解析:由题可得,令,即,解得或,又因为,所以.故选C.
3.若函数在区间上单调递增,则实数的取值范围是(
)
A.
B.
C.
D.
答案:C
解析:,.
函数在区间上单调递增,
,即,得.
当时,,
实数的取值范围是.故选C.
4.已知函数,则的单调递增区间为_________________.
答案:
解析:因为,,
所以.
由可得,所以或,
即的单调递增区间为.
5.已知,函数.
(1)若曲线在点处的切线与直线垂直,求的值;
(2)若函数在区间上单调递减,求的取值范围.
答案:(1)因为,
所以曲线在点处的切线斜率.
而直线的斜率为,则,得.
(2)由在上单调递减,
得在上恒成立,
即在上恒成立.
又时,,所以,
所以的取值范围是.
小结作业
小结:利用导数确定函数的单调性以及函数的单调区间.
作业:
四、板书设计
5.3.1
函数的单调性
1.
函数的单调性与导数的关系;
2.
形如的函数的单调性.
3.
函数的变化快慢与导数的关系.
