4.1数列(1)同步练习-2021-2022学年高二上学期数学苏教版(2019)选择性必修第一册Word含答案
文档属性
| 名称 | 4.1数列(1)同步练习-2021-2022学年高二上学期数学苏教版(2019)选择性必修第一册Word含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 61.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 00:00:00 | ||
图片预览

文档简介
4.1
数
列(1)
课本温习
1.
已知数列{an}的通项公式是an=,则这个数列的第5项a5等于( )
A.
1
B.
2
C.
D.
2.
数列{an}中,an=2n2-3,则125是这个数列的( )
A.
第4项
B.
第8项
C.
第7项
D.
第12项
3.
已知数列{an}的通项公式an=(n∈N
),则是这个数列的( )
A.
第10项
B.
第11项
C.
第12项
D.
第13项
4.
已知数列{an}的通项公式an=kn-5,且a8=1,则7为该数列的( )
A.
第13项
B.
第14项
C.
第15项
D.
第16项
5.
数列-1,3,-7,15,…的一个通项公式可以是( )
A.
an=(-1)n+1(2n-1)
B.
an=(-1)n(2n-1)
C.
an=(-1)n(2n-1-1)
D.
an=(-1)n(2n+1-1)
固基强能
6.
在数列{an}中,a1=,an+1=1-,则a5等于( )
A.
-1
B.
1
C.
-2
D.
2
7.
(多选)若数列{an}的通项公式为an=则a2·a3的值不可能为( )
A.
20
B.
30
C.
40
D.
50
8.
(多选)已知数列{an}的通项公式an=log(n+1)(n+2),则它的前n项之积可以是( )
A.
1
B.
3
C.
5
D.
7
9.
一个正整数数表如下(表中下一行中的数的个数是上一行中数的个数的2倍):
第1行
1
第2行
2 3
第3行
4 5 6 7
…
…
则第6行中的第4个数是________.
10.
写出下列数列的一个通项公式:
(1)
1,-3,5,-7,9,…;
(2)
1,0,,0,,0,,…;
(3)
-,2,-,8,-,…;
(4)
0.9,0.99,0.999,0.999
9,….
11.
已知数列{an}满足a1=a2=a,an=an-1+an-2,且a8=34,则a=________.
12.
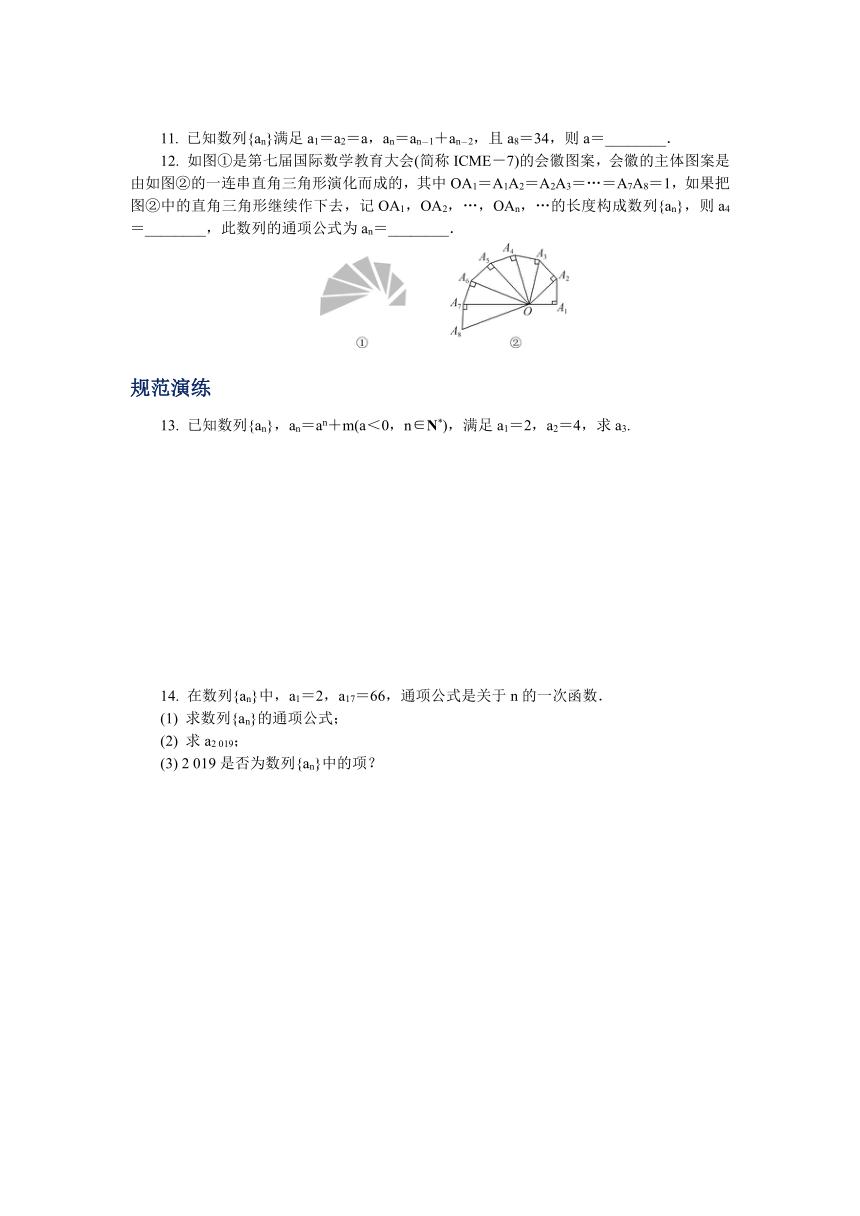
如图①是第七届国际数学教育大会(简称ICME-7)的会徽图案,会徽的主体图案是由如图②的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1,如果把图②中的直角三角形继续作下去,记OA1,OA2,…,OAn,…的长度构成数列{an},则a4=________,此数列的通项公式为an=________.
规范演练
13.
已知数列{an},an=an+m(a<0,n∈N
),满足a1=2,a2=4,求a3.
14.
在数列{an}中,a1=2,a17=66,通项公式是关于n的一次函数.
(1)
求数列{an}的通项公式;
(2)
求a2
019;
(3)
2
019是否为数列{an}中的项?
答案:
1.
D 解析:a5==.故选D.
2.
B 解析:令2n2-3=125得n=8或n=-8(舍),故125是第8项.
3.
C 解析:由题意知=,n∈N
,解得n=12.故选C.
4.
D 解析:由a8=8k-5=1,解得k=,∴
an=n-5.∴令n-5=7,解得n=16.故选D.
5.
B 解析:数列各项正、负交替,故可用(-1)n来调节.又1=21-1,3=22-1,7=23-1,15=24-1,…,所以通项公式为an=(-1)n·(2n-1).故选B.
6.
A 解析:由题意知a1=,an+1=1-,则a2=1-2=-1;a3=1+1=2;a4=1-=;a5=1-2=-1.故选A.
7.
BCD 解析:由an=得a2=2,a3=10,所以a2·a3=20.故选BCD.
8.
BCD 解析:a1·a2·a3·…·an=log23×log34×log45×…×logn+1(n+2)=××…×==log2(n+2).
9.
35 解析:由数表知,表中各行的第一个数依次为20,21,22,23,…,所以第6行的第一个数为25,所以第6行中的第4个数是35.
10.
解:(1)
an=(-1)n+1(2n-1).
(2)
an=.
(3)
an=(-1)n.
(4)
an=1-.
11.
解析:由题意an=an-1+an-2,得a3=a2+a1=2a,a4=a3+a2=3a,a5=a4+a3=5a,a6=a5+a4=8a,a7=a6+a5=13a,a8=a7+a6=21a.又a8=34,则21a=34,所以a=.
12.
2 解析:因为OA1=1,OA2=,OA3=,…,OAn=,…,
所以a1=1,a2=,a3=,…,an=.
13.
解:∵
∴
a2-a=2,∴
a=2或-1.
又a<0,∴
a=-1.
又a+m=2,∴
m=3,
∴
an=(-1)n+3,
∴
a3=(-1)3+3=2.
14.
解:(1)设an=kn+b(k≠0),则有
解得
∴
an=4n-2.
(2)a2
019=4×2
019-2=8
074.
(3)由4n-2=2
019得n=505.25?N
,
故2
019不是数列{an}中的项.
数
列(1)
课本温习
1.
已知数列{an}的通项公式是an=,则这个数列的第5项a5等于( )
A.
1
B.
2
C.
D.
2.
数列{an}中,an=2n2-3,则125是这个数列的( )
A.
第4项
B.
第8项
C.
第7项
D.
第12项
3.
已知数列{an}的通项公式an=(n∈N
),则是这个数列的( )
A.
第10项
B.
第11项
C.
第12项
D.
第13项
4.
已知数列{an}的通项公式an=kn-5,且a8=1,则7为该数列的( )
A.
第13项
B.
第14项
C.
第15项
D.
第16项
5.
数列-1,3,-7,15,…的一个通项公式可以是( )
A.
an=(-1)n+1(2n-1)
B.
an=(-1)n(2n-1)
C.
an=(-1)n(2n-1-1)
D.
an=(-1)n(2n+1-1)
固基强能
6.
在数列{an}中,a1=,an+1=1-,则a5等于( )
A.
-1
B.
1
C.
-2
D.
2
7.
(多选)若数列{an}的通项公式为an=则a2·a3的值不可能为( )
A.
20
B.
30
C.
40
D.
50
8.
(多选)已知数列{an}的通项公式an=log(n+1)(n+2),则它的前n项之积可以是( )
A.
1
B.
3
C.
5
D.
7
9.
一个正整数数表如下(表中下一行中的数的个数是上一行中数的个数的2倍):
第1行
1
第2行
2 3
第3行
4 5 6 7
…
…
则第6行中的第4个数是________.
10.
写出下列数列的一个通项公式:
(1)
1,-3,5,-7,9,…;
(2)
1,0,,0,,0,,…;
(3)
-,2,-,8,-,…;
(4)
0.9,0.99,0.999,0.999
9,….
11.
已知数列{an}满足a1=a2=a,an=an-1+an-2,且a8=34,则a=________.
12.
如图①是第七届国际数学教育大会(简称ICME-7)的会徽图案,会徽的主体图案是由如图②的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1,如果把图②中的直角三角形继续作下去,记OA1,OA2,…,OAn,…的长度构成数列{an},则a4=________,此数列的通项公式为an=________.
规范演练
13.
已知数列{an},an=an+m(a<0,n∈N
),满足a1=2,a2=4,求a3.
14.
在数列{an}中,a1=2,a17=66,通项公式是关于n的一次函数.
(1)
求数列{an}的通项公式;
(2)
求a2
019;
(3)
2
019是否为数列{an}中的项?
答案:
1.
D 解析:a5==.故选D.
2.
B 解析:令2n2-3=125得n=8或n=-8(舍),故125是第8项.
3.
C 解析:由题意知=,n∈N
,解得n=12.故选C.
4.
D 解析:由a8=8k-5=1,解得k=,∴
an=n-5.∴令n-5=7,解得n=16.故选D.
5.
B 解析:数列各项正、负交替,故可用(-1)n来调节.又1=21-1,3=22-1,7=23-1,15=24-1,…,所以通项公式为an=(-1)n·(2n-1).故选B.
6.
A 解析:由题意知a1=,an+1=1-,则a2=1-2=-1;a3=1+1=2;a4=1-=;a5=1-2=-1.故选A.
7.
BCD 解析:由an=得a2=2,a3=10,所以a2·a3=20.故选BCD.
8.
BCD 解析:a1·a2·a3·…·an=log23×log34×log45×…×logn+1(n+2)=××…×==log2(n+2).
9.
35 解析:由数表知,表中各行的第一个数依次为20,21,22,23,…,所以第6行的第一个数为25,所以第6行中的第4个数是35.
10.
解:(1)
an=(-1)n+1(2n-1).
(2)
an=.
(3)
an=(-1)n.
(4)
an=1-.
11.
解析:由题意an=an-1+an-2,得a3=a2+a1=2a,a4=a3+a2=3a,a5=a4+a3=5a,a6=a5+a4=8a,a7=a6+a5=13a,a8=a7+a6=21a.又a8=34,则21a=34,所以a=.
12.
2 解析:因为OA1=1,OA2=,OA3=,…,OAn=,…,
所以a1=1,a2=,a3=,…,an=.
13.
解:∵
∴
a2-a=2,∴
a=2或-1.
又a<0,∴
a=-1.
又a+m=2,∴
m=3,
∴
an=(-1)n+3,
∴
a3=(-1)3+3=2.
14.
解:(1)设an=kn+b(k≠0),则有
解得
∴
an=4n-2.
(2)a2
019=4×2
019-2=8
074.
(3)由4n-2=2
019得n=505.25?N
,
故2
019不是数列{an}中的项.
