河南省信阳市2020-2021学年高二下学期期末考试数学(理)试题 Word版含答案解析
文档属性
| 名称 | 河南省信阳市2020-2021学年高二下学期期末考试数学(理)试题 Word版含答案解析 |  | |
| 格式 | docx | ||
| 文件大小 | 958.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 08:48:35 | ||
图片预览




文档简介
信阳市2020-2021学年度高二下学期期末教学质量检测
数学(理科)试题
(测试时间:120分钟卷面总分:150分)
注意事项:
1.答题前,考生务必将自己的姓名、准考证号填写在本试卷相应的位置.
2.全部答案在答题卡上完成,答在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知复数之满足false,则复数false的共扼复数false所对应的点位于复平面的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知函数false,则false( )
A.false B.false C.false D.false
3.用反证法证明命题“自然数false,false,false中至少有一个偶数”,则证明的第一步,其正确的反设为( )
A.false,false,false都是奇数 B.false,false,false都是偶数
C.false,false,false至少有一个奇数 D.false,false,false至多有一个偶数
4.有一散点图如图所示,在false个false数据中去掉false后,给出下列说法:
①相关系数false变大;②相关指数false变大;
③残差平方和变小;④解释变量false与预报变量false的相关性变强.
其中正确说法的个数为( )
A.false个 B.false个 C.false个 D.false个
5.若false的展开式中各项系数之和为false,则展开式的常数项为( )
A.false B.false C.false D.false
6.函数false的单调递减区间为( )
A.false B.false C.false D.false
7.false与false的关系为( )
A.false B.false
C.false D.无法确定
8.在桥梁设计中,桥墩一般设计成圆柱形,因为其各向受力均衡,而且在相同截面下,浇筑用模最省.假设一桥梁施工队在浇筑桥墩时,采用由内向外扩张式浇筑,即保持圆柱高度不变,截面半径逐渐增大,设圆柱半径关于时间变化的函数为false.若圆柱的体积以均匀速度false增长,则圆柱的侧面积的增长速度与圆柱半径( )
A.成正比,比例系数为false B.成正比,比例系数为false
C.成反比,比例系数为false D.成反比,比例系数为false
9.2020年初,新型冠状肺炎在欧洲爆发后,我国第一时间内向相关国家捐助医疗物资,并派出由医疗专家组成的医疗小组奔赴相关国家.现有四个医疗小组甲、乙、丙、丁,和有false个需要援助的国家可供选择,每个医疗小组只去一个国家,设事件false“false个医疗小组去的国家各不相同”,事件false“小组甲独自去一个国家”,则false( )
A.false B.false C.false D.false
10.已知false,false恰有一个极值点false,则false的取值范围是( )
A.false B.false
C.false D.false
11.我们知道,在false次独立重复试验(即伯努利试验)中,每次试验中事件false发生的概率为false,则事件false发生的次数false服从二项分布false,事实上,在无限次伯努利试验中,另一个随机变量的实际应用也很广泛,即事件false首次发生时试验进行的次数false,显然false,false,false,false,…我们称false服从“几何分布”,经计算得false.由此推广,在无限次伯努利试验中,试验进行到事件false和false都发生后停止,此时所进行的实验次数记为false,则false,false,false,…,那么false( )
A.false B.false C.false D.false
12.已知函数false,false,若存在false,false,使得false成立,则false的最大值为( )
A.false B.false C.false D.false
二、填空题:本大题共4小题,每小题5分,共20分.
13.经研究发现:任意一个三次多项式函数false的图象都只有一个对称中心点false,其中false是false的根,false是false的导数,false是false的导数.若函数false图象的对称中心点为false,则false,false的值依次为 .
14.2021年1月某校高三年级false名学生参加了教育局组织的期末统考,已知数学考试成绩false(试卷满分为false分).统计结果显示数学考试成绩在false分到false分之间的人数约为总人数的false,则此次统考中成绩不低于false分的学生人数约为 .
15.我们知道,当false时,可以得到不等式false,当false时,可以得到不等式false,由此可以推广:当false时,其中false,false,得到的不等式是 .
16.已知false,则曲线false在false处的切线方程为 _.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知false为虚数单位,关于false的方程false的两根分别为false,false.若false,求实数false的值.
18.设false(false,false),若false的展开式中,存在某连续false项,其二项式系数依次成等差数列,则称false具有性质false.
(1)求证:false具有性质false.
(2)若存在false,使false具有性质false,求false的最大值.
19.某互联网公司为了确定下一季度的前期广告投入计划,收集了近false个月广告投入量false(单位:万元)和收益(单位:万元)的数据如下表:
月份
false
false
false
false
false
false
广告投入量
false
false
false
false
false
false
收益
false
false
false
false
false
false
他们分别用两种模型①false,②false分别进行拟合,得到相应的回归方程并进行残差分析,得到如下图所示的残差图及一些统计量的值.
false
false
false
false
false
false
false
false
(1)根据残差图,比较模型①②的拟合效果,应该选择哪个模型?请说明理由.
(2)残差绝对值大于false的数据认为是异常数据,需要剔除.
(1)剔除异常数据后求出(1)中所选模型的回归方程;
(2)若广告投入量false,求该模型收益的预报值是多少?
附:回归方程false中斜率和截距的最小二乘估计公式分别为:
false;false.
20.已知false是函数false的导函数,且false,当false时,false.
(1)证明:当false时,函数false是增函数;
(2)解不等式false.
21.某校为了解校园安全教育系列活动的成效,对全校学生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记false分,“不合格”记false分.现随机抽取部分学生的成绩,统计结果及对应的频率分布直方图如下所示:
等级
不合格
合格
得分
false
false
false
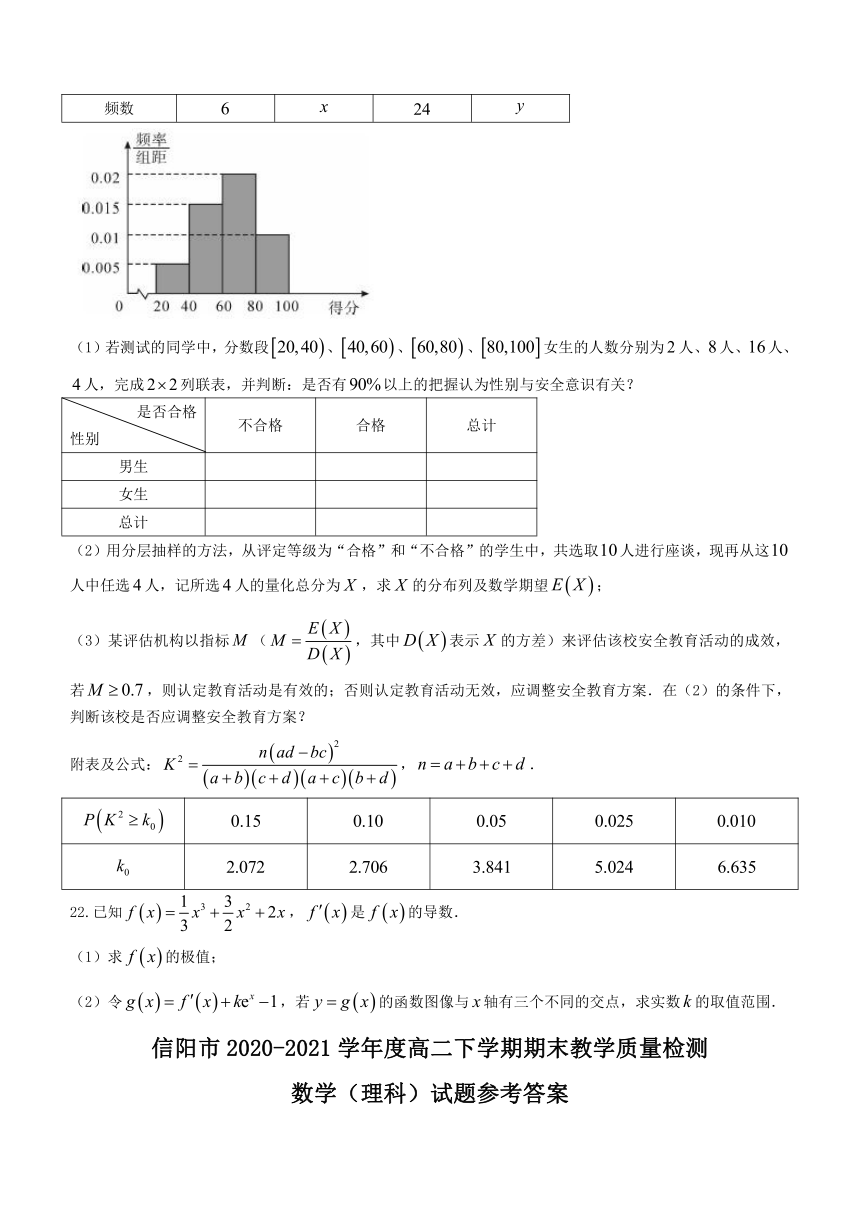
false
频数
false
false
false
false
(1)若测试的同学中,分数段false、false、false、false女生的人数分别为false人、false人、false人、false人,完成false列联表,并判断:是否有false以上的把握认为性别与安全意识有关?
-67945-3810是否合格
性别
不合格
合格
总计
男生
女生
总计
(2)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中,共选取false人进行座谈,现再从这false人中任选false人,记所选false人的量化总分为false,求false的分布列及数学期望false;
(3)某评估机构以指标false(false,其中false表示false的方差)来评估该校安全教育活动的成效,若false,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(2)的条件下,判断该校是否应调整安全教育方案?
附表及公式:false,false.
false
false
false
false
false
false
false
false
false
false
false
false
22.已知false,false是false的导数.
(1)求false的极值;
(2)令false,若false的函数图像与false轴有三个不同的交点,求实数false的取值范围.
信阳市2020-2021学年度高二下学期期末教学质量检测
数学(理科)试题参考答案
一、选择题
题号
false
false
false
false
false
false
false
false
false
false
false
false
答案
false
false
false
false
false
false
false
false
false
false
false
false
1.由题意得false,则false,所以false所对应的点位于复平面的第四象限.故选false.
2.由常见导数公式及导数的四则运算法则,可得false.故选false.
3.命题“自然数false,false,false中至少有一个偶数”的否定为“自然数false,false,false中没有偶数”,即“自然数false,false,false都是奇数”.故选false.
4.由散点图可知,去掉false后,false与false的相关性加强,并且是正相关,所以相关系数false变大,相关指数false变大,残差平方和变小,所以四个命题都正确.故选false.
5.令false得展开式中的各项系数和为false,解得false,所以展开式的通项为false,令false得展开式的常数项为false.故选false.
6.函数false的定义域为false,false,由false解得false,所以函数false的单调递减区间为false.故选false.
7.false,false,而false,false,false,所以false,所以false.故选false.
8.设圆柱高度为false,由false,知false,即false,所以false.
又圆柱的侧面积false,则其侧面积的增长速度false,所以圆柱的侧面积的增长速度与圆柱半径成反比,比例系数为false.故选false.
9.由题意知false,false,所以false.故选false.
10.由题意得falsefalse.
false,false恰有一个极值点false,
false在false上无解,即false在false上无解.
令false,则false,
false函数false在false上单调递增,当false时,false,
false.故选false.
11.由false得falsefalse
false
false
false.故选false.
12.函数false的定义域为false,false,所
以当false时,false,false单调递增,当false时,false,false单调递减,
注意false,所以false时,false时;
false,false;false时,false,
同时注意到false,
所以若存在false,false,使得false成立,
则false且false,
false,
false,
false,
令false,false,则false,
令false,解得false,令false,解得false,
false在false上单调递增,在false上单调递减,
false.故选false.
二、填空题
13.false,false 14.false 15.false 16.false
13.因为false,所以false,所以false,
又false的对称中心为false,所以false,解得false,
由false,解得false.
14.因为false,所以其正态曲线关于直线false对称.
又成绩在false分到false分之间的人数约为总人数的false,
所以成绩不低于false分的学生人数占总人数的false.
所以成绩不低于false分的学生人数约为false.
15.由类比推理可得得到的不等式是false.
16.false,令false得false,解得false,所以false,false,则false,false,所以曲线false在false处的切线方程为false,即false.
三、解答题
17.把false代入关于false的方程false得false.
解得false.
false的值为false.
18.(1)false的展开式中第二、三、四项的二项式系数分别为false,false,false,
因为false,即false,false,false成等差数列,所以false具有性质false.
(2)设false具有性质false,则存在false,false,使false,false,false成等差数列,
所以false,
整理得:false,
即false,
所以false为完全平方数,
又false,由于false,
所以false的最大值为false,此时false或false.
19.(1)应该选择模型①,因为模型①的残差点比较均匀地落在水平的带状区域中,且模型①的带状区域比模型②的带状区域窄,所以模型①的拟合精度高,回归方程的预报精度高.
(2)①剔除异常数据,即false月份的数据后,得
false,false.
false,false.
false,false.
所以false关于false的回归方程为false.
②把false代入①中所求回归方程得false,故预报值为false万元.
20.(1)证明:false,
false.
false当false时,false,
false当false时,false.
false在false上是增函数.
(2)false,
falsefalse.
false是偶函数.
又false,
false,即false.
false,即false,解得false.
故不等式false的解集为false.
21.(1)由频率分布直方图可知,得分在false的频率为false,
故抽取的学生答卷总数为false,
false,false.
性别与合格情况的false列联表为:
-67945-3810是否合格
性别
不合格
合格
总计
男生
false
false
false
女生
false
false
false
总计
false
false
false
false
即在犯错误概率不超过false的前提下,不能认为性别与安全测试是否合格有关.
(2)“不合格”和“合格”的人数比例为false,因此抽取的false人中“不合格”有false人,“合格”有false人,
所以false可能的取值为false、false、false、false,
false,false.
false
false,false.
false的分布列为:
false
false
false
false
false
false
false
false
false
false
false
false
所以false.
(3)由(2)知:falsefalse
false.
故我们认为该校的安全教育活动是有效的,不雭要调整安全教育方案.
22.(1)因为false,
令false,得false,false,
当false变化时,false,false的变化如下表所示:
false
false
false
false
false
false
false
false
false
false
false
false
false
false
极大值
false
极小值
false
由上表可知,false,false.
(2)由(1)知false,
由题知需false有三个不同的解,即false有三个不同的解.
设false,则false,
当false时,false,false单调递增,当false时,false,false单调递减,
当false时,false,false单调递增,又当false时,false,当false时,false且false,且false,false.
作出函数false的简图如图:
数形结合可知:false.
注:考虑学生只是高二年级,故参考答案给出的是极限以及借助图象求解,但是实际上这是不严谨的,下面给出严谨的证明过程(即取点证明):
当false时,false,false,所以存在唯一false使得false;
又false,false所以存在唯一false使得false;
当false时,false,则false,又当false时,false,则false,
所以false,所以false,且false,
所以存在唯一false使得false;
所以当false时false有三个不同的解,即false的函数图象与false轴有三个不同的交点.
数学(理科)试题
(测试时间:120分钟卷面总分:150分)
注意事项:
1.答题前,考生务必将自己的姓名、准考证号填写在本试卷相应的位置.
2.全部答案在答题卡上完成,答在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知复数之满足false,则复数false的共扼复数false所对应的点位于复平面的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知函数false,则false( )
A.false B.false C.false D.false
3.用反证法证明命题“自然数false,false,false中至少有一个偶数”,则证明的第一步,其正确的反设为( )
A.false,false,false都是奇数 B.false,false,false都是偶数
C.false,false,false至少有一个奇数 D.false,false,false至多有一个偶数
4.有一散点图如图所示,在false个false数据中去掉false后,给出下列说法:
①相关系数false变大;②相关指数false变大;
③残差平方和变小;④解释变量false与预报变量false的相关性变强.
其中正确说法的个数为( )
A.false个 B.false个 C.false个 D.false个
5.若false的展开式中各项系数之和为false,则展开式的常数项为( )
A.false B.false C.false D.false
6.函数false的单调递减区间为( )
A.false B.false C.false D.false
7.false与false的关系为( )
A.false B.false
C.false D.无法确定
8.在桥梁设计中,桥墩一般设计成圆柱形,因为其各向受力均衡,而且在相同截面下,浇筑用模最省.假设一桥梁施工队在浇筑桥墩时,采用由内向外扩张式浇筑,即保持圆柱高度不变,截面半径逐渐增大,设圆柱半径关于时间变化的函数为false.若圆柱的体积以均匀速度false增长,则圆柱的侧面积的增长速度与圆柱半径( )
A.成正比,比例系数为false B.成正比,比例系数为false
C.成反比,比例系数为false D.成反比,比例系数为false
9.2020年初,新型冠状肺炎在欧洲爆发后,我国第一时间内向相关国家捐助医疗物资,并派出由医疗专家组成的医疗小组奔赴相关国家.现有四个医疗小组甲、乙、丙、丁,和有false个需要援助的国家可供选择,每个医疗小组只去一个国家,设事件false“false个医疗小组去的国家各不相同”,事件false“小组甲独自去一个国家”,则false( )
A.false B.false C.false D.false
10.已知false,false恰有一个极值点false,则false的取值范围是( )
A.false B.false
C.false D.false
11.我们知道,在false次独立重复试验(即伯努利试验)中,每次试验中事件false发生的概率为false,则事件false发生的次数false服从二项分布false,事实上,在无限次伯努利试验中,另一个随机变量的实际应用也很广泛,即事件false首次发生时试验进行的次数false,显然false,false,false,false,…我们称false服从“几何分布”,经计算得false.由此推广,在无限次伯努利试验中,试验进行到事件false和false都发生后停止,此时所进行的实验次数记为false,则false,false,false,…,那么false( )
A.false B.false C.false D.false
12.已知函数false,false,若存在false,false,使得false成立,则false的最大值为( )
A.false B.false C.false D.false
二、填空题:本大题共4小题,每小题5分,共20分.
13.经研究发现:任意一个三次多项式函数false的图象都只有一个对称中心点false,其中false是false的根,false是false的导数,false是false的导数.若函数false图象的对称中心点为false,则false,false的值依次为 .
14.2021年1月某校高三年级false名学生参加了教育局组织的期末统考,已知数学考试成绩false(试卷满分为false分).统计结果显示数学考试成绩在false分到false分之间的人数约为总人数的false,则此次统考中成绩不低于false分的学生人数约为 .
15.我们知道,当false时,可以得到不等式false,当false时,可以得到不等式false,由此可以推广:当false时,其中false,false,得到的不等式是 .
16.已知false,则曲线false在false处的切线方程为 _.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知false为虚数单位,关于false的方程false的两根分别为false,false.若false,求实数false的值.
18.设false(false,false),若false的展开式中,存在某连续false项,其二项式系数依次成等差数列,则称false具有性质false.
(1)求证:false具有性质false.
(2)若存在false,使false具有性质false,求false的最大值.
19.某互联网公司为了确定下一季度的前期广告投入计划,收集了近false个月广告投入量false(单位:万元)和收益(单位:万元)的数据如下表:
月份
false
false
false
false
false
false
广告投入量
false
false
false
false
false
false
收益
false
false
false
false
false
false
他们分别用两种模型①false,②false分别进行拟合,得到相应的回归方程并进行残差分析,得到如下图所示的残差图及一些统计量的值.
false
false
false
false
false
false
false
false
(1)根据残差图,比较模型①②的拟合效果,应该选择哪个模型?请说明理由.
(2)残差绝对值大于false的数据认为是异常数据,需要剔除.
(1)剔除异常数据后求出(1)中所选模型的回归方程;
(2)若广告投入量false,求该模型收益的预报值是多少?
附:回归方程false中斜率和截距的最小二乘估计公式分别为:
false;false.
20.已知false是函数false的导函数,且false,当false时,false.
(1)证明:当false时,函数false是增函数;
(2)解不等式false.
21.某校为了解校园安全教育系列活动的成效,对全校学生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记false分,“不合格”记false分.现随机抽取部分学生的成绩,统计结果及对应的频率分布直方图如下所示:
等级
不合格
合格
得分
false
false
false
false
频数
false
false
false
false
(1)若测试的同学中,分数段false、false、false、false女生的人数分别为false人、false人、false人、false人,完成false列联表,并判断:是否有false以上的把握认为性别与安全意识有关?
-67945-3810是否合格
性别
不合格
合格
总计
男生
女生
总计
(2)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中,共选取false人进行座谈,现再从这false人中任选false人,记所选false人的量化总分为false,求false的分布列及数学期望false;
(3)某评估机构以指标false(false,其中false表示false的方差)来评估该校安全教育活动的成效,若false,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(2)的条件下,判断该校是否应调整安全教育方案?
附表及公式:false,false.
false
false
false
false
false
false
false
false
false
false
false
false
22.已知false,false是false的导数.
(1)求false的极值;
(2)令false,若false的函数图像与false轴有三个不同的交点,求实数false的取值范围.
信阳市2020-2021学年度高二下学期期末教学质量检测
数学(理科)试题参考答案
一、选择题
题号
false
false
false
false
false
false
false
false
false
false
false
false
答案
false
false
false
false
false
false
false
false
false
false
false
false
1.由题意得false,则false,所以false所对应的点位于复平面的第四象限.故选false.
2.由常见导数公式及导数的四则运算法则,可得false.故选false.
3.命题“自然数false,false,false中至少有一个偶数”的否定为“自然数false,false,false中没有偶数”,即“自然数false,false,false都是奇数”.故选false.
4.由散点图可知,去掉false后,false与false的相关性加强,并且是正相关,所以相关系数false变大,相关指数false变大,残差平方和变小,所以四个命题都正确.故选false.
5.令false得展开式中的各项系数和为false,解得false,所以展开式的通项为false,令false得展开式的常数项为false.故选false.
6.函数false的定义域为false,false,由false解得false,所以函数false的单调递减区间为false.故选false.
7.false,false,而false,false,false,所以false,所以false.故选false.
8.设圆柱高度为false,由false,知false,即false,所以false.
又圆柱的侧面积false,则其侧面积的增长速度false,所以圆柱的侧面积的增长速度与圆柱半径成反比,比例系数为false.故选false.
9.由题意知false,false,所以false.故选false.
10.由题意得falsefalse.
false,false恰有一个极值点false,
false在false上无解,即false在false上无解.
令false,则false,
false函数false在false上单调递增,当false时,false,
false.故选false.
11.由false得falsefalse
false
false
false.故选false.
12.函数false的定义域为false,false,所
以当false时,false,false单调递增,当false时,false,false单调递减,
注意false,所以false时,false时;
false,false;false时,false,
同时注意到false,
所以若存在false,false,使得false成立,
则false且false,
false,
false,
false,
令false,false,则false,
令false,解得false,令false,解得false,
false在false上单调递增,在false上单调递减,
false.故选false.
二、填空题
13.false,false 14.false 15.false 16.false
13.因为false,所以false,所以false,
又false的对称中心为false,所以false,解得false,
由false,解得false.
14.因为false,所以其正态曲线关于直线false对称.
又成绩在false分到false分之间的人数约为总人数的false,
所以成绩不低于false分的学生人数占总人数的false.
所以成绩不低于false分的学生人数约为false.
15.由类比推理可得得到的不等式是false.
16.false,令false得false,解得false,所以false,false,则false,false,所以曲线false在false处的切线方程为false,即false.
三、解答题
17.把false代入关于false的方程false得false.
解得false.
false的值为false.
18.(1)false的展开式中第二、三、四项的二项式系数分别为false,false,false,
因为false,即false,false,false成等差数列,所以false具有性质false.
(2)设false具有性质false,则存在false,false,使false,false,false成等差数列,
所以false,
整理得:false,
即false,
所以false为完全平方数,
又false,由于false,
所以false的最大值为false,此时false或false.
19.(1)应该选择模型①,因为模型①的残差点比较均匀地落在水平的带状区域中,且模型①的带状区域比模型②的带状区域窄,所以模型①的拟合精度高,回归方程的预报精度高.
(2)①剔除异常数据,即false月份的数据后,得
false,false.
false,false.
false,false.
所以false关于false的回归方程为false.
②把false代入①中所求回归方程得false,故预报值为false万元.
20.(1)证明:false,
false.
false当false时,false,
false当false时,false.
false在false上是增函数.
(2)false,
falsefalse.
false是偶函数.
又false,
false,即false.
false,即false,解得false.
故不等式false的解集为false.
21.(1)由频率分布直方图可知,得分在false的频率为false,
故抽取的学生答卷总数为false,
false,false.
性别与合格情况的false列联表为:
-67945-3810是否合格
性别
不合格
合格
总计
男生
false
false
false
女生
false
false
false
总计
false
false
false
false
即在犯错误概率不超过false的前提下,不能认为性别与安全测试是否合格有关.
(2)“不合格”和“合格”的人数比例为false,因此抽取的false人中“不合格”有false人,“合格”有false人,
所以false可能的取值为false、false、false、false,
false,false.
false
false,false.
false的分布列为:
false
false
false
false
false
false
false
false
false
false
false
false
所以false.
(3)由(2)知:falsefalse
false.
故我们认为该校的安全教育活动是有效的,不雭要调整安全教育方案.
22.(1)因为false,
令false,得false,false,
当false变化时,false,false的变化如下表所示:
false
false
false
false
false
false
false
false
false
false
false
false
false
false
极大值
false
极小值
false
由上表可知,false,false.
(2)由(1)知false,
由题知需false有三个不同的解,即false有三个不同的解.
设false,则false,
当false时,false,false单调递增,当false时,false,false单调递减,
当false时,false,false单调递增,又当false时,false,当false时,false且false,且false,false.
作出函数false的简图如图:
数形结合可知:false.
注:考虑学生只是高二年级,故参考答案给出的是极限以及借助图象求解,但是实际上这是不严谨的,下面给出严谨的证明过程(即取点证明):
当false时,false,false,所以存在唯一false使得false;
又false,false所以存在唯一false使得false;
当false时,false,则false,又当false时,false,则false,
所以false,所以false,且false,
所以存在唯一false使得false;
所以当false时false有三个不同的解,即false的函数图象与false轴有三个不同的交点.
同课章节目录
