《第三章 勾股定理》单元测试题 (含答案)
文档属性
| 名称 | 《第三章 勾股定理》单元测试题 (含答案) | 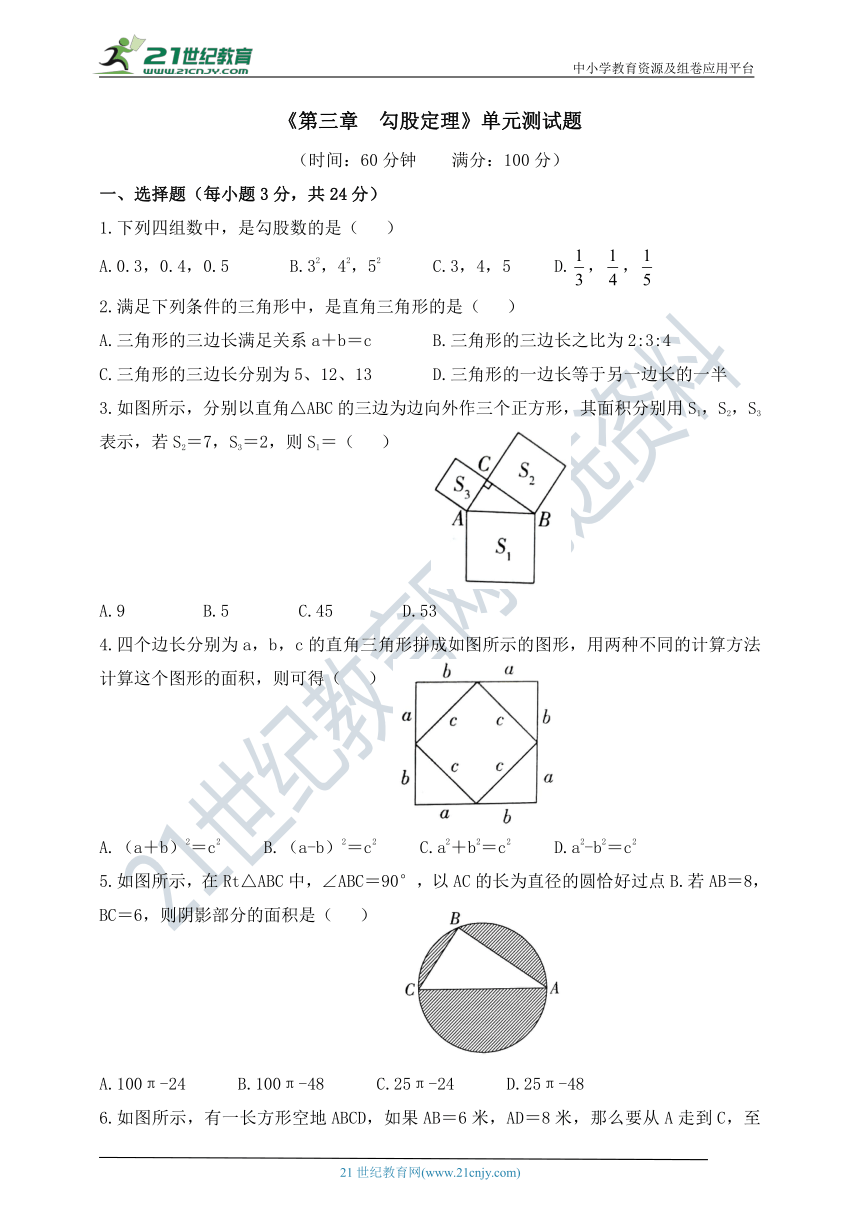 | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 18:32:37 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
《第三章 勾股定理》单元测试题
(时间:60分钟 满分:100分)
一、选择题(每小题3分,共24分)
1.下列四组数中,是勾股数的是( )
A.0.3,0.4,0.5 B.32,42,52 C.3,4,5 D.,,
2.满足下列条件的三角形中,是直角三角形的是( )
A.三角形的三边长满足关系a+b=c B.三角形的三边长之比为2:3:4
C.三角形的三边长分别为5、12、13 D.三角形的一边长等于另一边长的一半
3.如图所示,分别以直角△ABC的三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,若S2=7,S3=2,则S1=( )
A.9 B.5 C.45 D.53
4.四个边长分别为a,b,c的直角三角形拼成如图所示的图形,用两种不同的计算方法计算这个图形的面积,则可得( )
A.(a+b)2=c2 B.(a-b)2=c2 C.a2+b2=c2 D.a2-b2=c2
5.如图所示,在Rt△ABC中,∠ABC=90°,以AC的长为直径的圆恰好过点B.若AB=8,BC=6,则阴影部分的面积是( )
A.100π-24 B.100π-48 C.25π-24 D.25π-48
6.如图所示,有一长方形空地ABCD,如果AB=6米,AD=8米,那么要从A走到C,至少要走( )
A.6米 B.8米 C.10米 D.14米
7.如图所示,圆柱的高为8cm,底面半径为cm,一只蚂蚁从点A沿圆柱外壁爬到点B处吃食,要爬行的最短路程是( )
A.6 cm B.8 cm C.10 cm D.12 cm
8.如图所示,有一张直角三角形纸片ABC,两条直角边AC=5,BC=10,将△ABC折叠,使点A和点B重合,折痕为DE,则CD的长为( )
A.1.8 B.2.5 C.3 D.3.75
二、填空题(每小题4分,共24分)
9.在Rt△ABC中,∠C=90°,AB=15,BC:AC=3:4,则BC=__________.
10.如图所示,AC⊥CE,AD=BE=13,BC=5,DE=7,则AC=__________.
11.如图所示,在高为3米,坡面长度AB为5米的楼梯表面铺上地毯,则至少需要地毯__________米.
12.如图所示,学校操场边上一块空地(阴影部分)需要绿化,测出CD=6m,AD=8m,BC=24m,AB=26m,AD⊥CD,那么需要绿化部分的面积为_________.
13.已知直角三角形的三边长分别为6、8、x,则以x为边长的正方形的面积为_________.
14.如图所示,在Rt△ABC中,∠BCA=90°,点D是BC上一点,AD=BD,若AB=8,BD=5,则CD=__________.
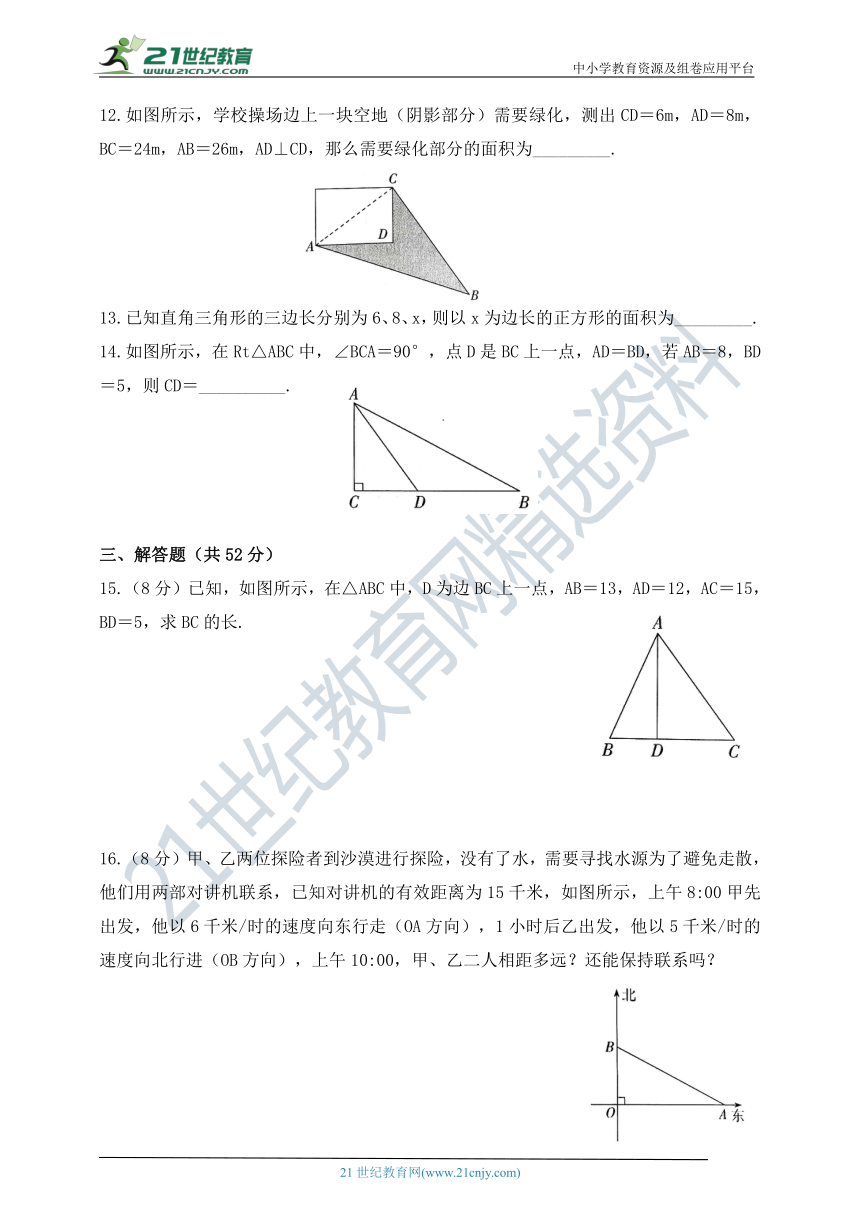
三、解答题(共52分)
15.(8分)已知,如图所示,在△ABC中,D为边BC上一点,AB=13,AD=12,AC=15,BD=5,求BC的长.
16.(8分)甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源为了避免走散,他们用两部对讲机联系,已知对讲机的有效距离为15千米,如图所示,上午8:00甲先出发,他以6千米/时的速度向东行走(OA方向),1小时后乙出发,他以5千米/时的速度向北行进(OB方向),上午10:00,甲、乙二人相距多远?还能保持联系吗?
17.(8分)新冠疫情期间,为了提高人民群众防疫意识,很多地方的宣讲车开起来了,大喇叭响起来了,宣传横幅挂起来了,电子屏亮起来了,电视、广播、微信、短信齐上阵,防疫标语、宣传金句频出,这传递着打赢疫情防控阻击战的坚定决心.如图所示,在一条笔直公路MN的一侧点A处有一村庄,村庄A到公路MN的距离AB为800米,若宣讲车周围1000米以内能听到广播宣传,宣讲车在公路MN上沿MN方向行驶.
(1)请问村庄A能否听到宣传?请说明理由;
(2)如果能听到,已知宣讲车的速度是300米/分钟,那么村庄A总共能听到多长时间的宣传?
18.(8分)如图所示,在长方形ABCD中,DC=9,在DC上找一点E,沿直线AE把△AED折叠,使D点恰好落在BC上,设这一点为F,若△ABF的面积是54,求DE的长.
19.(10分)观察下列勾股数:3,4,5;5,12,13;7,24,25;9,40,41;…;a,b,c.
请根据你发现的规律,回答下列问题:
(1)当a=19时,求b,c的值;
(2)当a=2n+1时,求b,c的值;
(3)用(2)的结论判断15,111,112是不是一组勾股数,并说明理由.
20.(10分)如图所示,对任意符合条件的Rt△BAC,绕其锐角顶点A逆时针旋转90°得到△EAD,所以∠BAE=90°,连接BE,延长DE、BC,交于点F,易知四边形ACFD是一个正方形,它的面积和四边形ABFE的面积相等,四边形ABFE的面积等于Rt△BAE和Rt△BFE的面积之和,根据图形写出一种证明勾股定理的方法.
参考答案
一、选择题
1.C 2.C 3.A 4.C 5.C 6.C 7.C 8.D
二、填空题
9. 9 10. 12 11. 7 12. 96 cm2 13. 100或28 14. 1.4
三、解答题
15.解析:∵AD2+BD2=144+25=169,AB2=169,
∴AD2+BD2=AB2,∴AD⊥BC,∴∠ADC=90°,
∴CD2=AC2-AD2=152-122=92,∴CD=9,∴BC=CD+BD=9+5=14.
16.解析 甲从上午8:00到上午10:00一共走了2小时,走了12千米,即OA=12千米.
乙从上午9:00到上午10:00一共走了1小时,走了5千米,即OB=5千米.
在Rt△OAB中,AB2=122+52=169,∴AB=13千米,
因此,上午10:00,甲、乙两人相距13千米.
∵15>13,∴甲、乙两人还能保持联系.
答:上午10:00,甲、乙两人相距13千米,两人还能保持联系.
17.解析(1)村庄A能听到宣传,
理由:∵村庄A到公路MN的距离AB为800米<1000米,
∴村庄A能听到宣传.
(2)如图,假设当宣讲车行驶到P点时,村庄A开始听到宣传,行驶到Q点时,村庄A听不到宣传,则AP=AQ=1000米,又∵AB=800米,
∴BP2=BQ2=10002-8002=6002,∴BP=BQ=600米,PQ=1200米,
∴村庄A总共听到宣传的时间为1200÷300=4分钟,
∴村庄A总共能听到4分钟的宣传.
18.解析 因为AB·BF=54,DC=AB=9,,所以BF=12.
所以AF2=92+122=225,∴AF=15.
所以BC=AD=AF=15,所以CF=BC-BF=15-12=3.
设DE=x,则CE=9-x,EF=DE=x.
则x2=(9-x)2+32,所以x=5.
所以DE的长为5.
19.解析 (1)观察给出的勾股数得,斜边长与较长直角边长的差是1,即c-b=1.
∵a=19,a2+b2=c2,∴192+b2=(b+1)2,
∴b=180,∴c=181.
(2)由(1)知c-b=1,∵a=2n+1,∴(2n+1)2+b2=c2,
∴c2-b2=(2n+1)2,即(c+b)(c-b)=(2n+1)2,
∴b+c=(2n+1)2,又c=b+1,∴2b+1=(2n+1)2,
∴b=2n2+2n,∴c=2n2+2n+1.
(3)15,111,112不是一组勾股数.
理由:由(2)知,2n+1,2n2+2n,2n2+2n+1为一组勾股数,
当2n+1=15时,n=7,但2n2+2n=2×72+2×7=112≠111,2n2+2n+1=113≠112,∴15,111,112不是一组勾股数.
20.解析 由题图可得正方形ACFD的面积=四边形ABFE的面积=Rt△BAE和Rt△BFE的面积之和,即S正方形ACFD=S△BAE+S△BFE,
∴b2=c2+,整理,得a2+b2=c2.
_21?????????è?????(www.21cnjy.com)_
《第三章 勾股定理》单元测试题
(时间:60分钟 满分:100分)
一、选择题(每小题3分,共24分)
1.下列四组数中,是勾股数的是( )
A.0.3,0.4,0.5 B.32,42,52 C.3,4,5 D.,,
2.满足下列条件的三角形中,是直角三角形的是( )
A.三角形的三边长满足关系a+b=c B.三角形的三边长之比为2:3:4
C.三角形的三边长分别为5、12、13 D.三角形的一边长等于另一边长的一半
3.如图所示,分别以直角△ABC的三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,若S2=7,S3=2,则S1=( )
A.9 B.5 C.45 D.53
4.四个边长分别为a,b,c的直角三角形拼成如图所示的图形,用两种不同的计算方法计算这个图形的面积,则可得( )
A.(a+b)2=c2 B.(a-b)2=c2 C.a2+b2=c2 D.a2-b2=c2
5.如图所示,在Rt△ABC中,∠ABC=90°,以AC的长为直径的圆恰好过点B.若AB=8,BC=6,则阴影部分的面积是( )
A.100π-24 B.100π-48 C.25π-24 D.25π-48
6.如图所示,有一长方形空地ABCD,如果AB=6米,AD=8米,那么要从A走到C,至少要走( )
A.6米 B.8米 C.10米 D.14米
7.如图所示,圆柱的高为8cm,底面半径为cm,一只蚂蚁从点A沿圆柱外壁爬到点B处吃食,要爬行的最短路程是( )
A.6 cm B.8 cm C.10 cm D.12 cm
8.如图所示,有一张直角三角形纸片ABC,两条直角边AC=5,BC=10,将△ABC折叠,使点A和点B重合,折痕为DE,则CD的长为( )
A.1.8 B.2.5 C.3 D.3.75
二、填空题(每小题4分,共24分)
9.在Rt△ABC中,∠C=90°,AB=15,BC:AC=3:4,则BC=__________.
10.如图所示,AC⊥CE,AD=BE=13,BC=5,DE=7,则AC=__________.
11.如图所示,在高为3米,坡面长度AB为5米的楼梯表面铺上地毯,则至少需要地毯__________米.
12.如图所示,学校操场边上一块空地(阴影部分)需要绿化,测出CD=6m,AD=8m,BC=24m,AB=26m,AD⊥CD,那么需要绿化部分的面积为_________.
13.已知直角三角形的三边长分别为6、8、x,则以x为边长的正方形的面积为_________.
14.如图所示,在Rt△ABC中,∠BCA=90°,点D是BC上一点,AD=BD,若AB=8,BD=5,则CD=__________.
三、解答题(共52分)
15.(8分)已知,如图所示,在△ABC中,D为边BC上一点,AB=13,AD=12,AC=15,BD=5,求BC的长.
16.(8分)甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源为了避免走散,他们用两部对讲机联系,已知对讲机的有效距离为15千米,如图所示,上午8:00甲先出发,他以6千米/时的速度向东行走(OA方向),1小时后乙出发,他以5千米/时的速度向北行进(OB方向),上午10:00,甲、乙二人相距多远?还能保持联系吗?
17.(8分)新冠疫情期间,为了提高人民群众防疫意识,很多地方的宣讲车开起来了,大喇叭响起来了,宣传横幅挂起来了,电子屏亮起来了,电视、广播、微信、短信齐上阵,防疫标语、宣传金句频出,这传递着打赢疫情防控阻击战的坚定决心.如图所示,在一条笔直公路MN的一侧点A处有一村庄,村庄A到公路MN的距离AB为800米,若宣讲车周围1000米以内能听到广播宣传,宣讲车在公路MN上沿MN方向行驶.
(1)请问村庄A能否听到宣传?请说明理由;
(2)如果能听到,已知宣讲车的速度是300米/分钟,那么村庄A总共能听到多长时间的宣传?
18.(8分)如图所示,在长方形ABCD中,DC=9,在DC上找一点E,沿直线AE把△AED折叠,使D点恰好落在BC上,设这一点为F,若△ABF的面积是54,求DE的长.
19.(10分)观察下列勾股数:3,4,5;5,12,13;7,24,25;9,40,41;…;a,b,c.
请根据你发现的规律,回答下列问题:
(1)当a=19时,求b,c的值;
(2)当a=2n+1时,求b,c的值;
(3)用(2)的结论判断15,111,112是不是一组勾股数,并说明理由.
20.(10分)如图所示,对任意符合条件的Rt△BAC,绕其锐角顶点A逆时针旋转90°得到△EAD,所以∠BAE=90°,连接BE,延长DE、BC,交于点F,易知四边形ACFD是一个正方形,它的面积和四边形ABFE的面积相等,四边形ABFE的面积等于Rt△BAE和Rt△BFE的面积之和,根据图形写出一种证明勾股定理的方法.
参考答案
一、选择题
1.C 2.C 3.A 4.C 5.C 6.C 7.C 8.D
二、填空题
9. 9 10. 12 11. 7 12. 96 cm2 13. 100或28 14. 1.4
三、解答题
15.解析:∵AD2+BD2=144+25=169,AB2=169,
∴AD2+BD2=AB2,∴AD⊥BC,∴∠ADC=90°,
∴CD2=AC2-AD2=152-122=92,∴CD=9,∴BC=CD+BD=9+5=14.
16.解析 甲从上午8:00到上午10:00一共走了2小时,走了12千米,即OA=12千米.
乙从上午9:00到上午10:00一共走了1小时,走了5千米,即OB=5千米.
在Rt△OAB中,AB2=122+52=169,∴AB=13千米,
因此,上午10:00,甲、乙两人相距13千米.
∵15>13,∴甲、乙两人还能保持联系.
答:上午10:00,甲、乙两人相距13千米,两人还能保持联系.
17.解析(1)村庄A能听到宣传,
理由:∵村庄A到公路MN的距离AB为800米<1000米,
∴村庄A能听到宣传.
(2)如图,假设当宣讲车行驶到P点时,村庄A开始听到宣传,行驶到Q点时,村庄A听不到宣传,则AP=AQ=1000米,又∵AB=800米,
∴BP2=BQ2=10002-8002=6002,∴BP=BQ=600米,PQ=1200米,
∴村庄A总共听到宣传的时间为1200÷300=4分钟,
∴村庄A总共能听到4分钟的宣传.
18.解析 因为AB·BF=54,DC=AB=9,,所以BF=12.
所以AF2=92+122=225,∴AF=15.
所以BC=AD=AF=15,所以CF=BC-BF=15-12=3.
设DE=x,则CE=9-x,EF=DE=x.
则x2=(9-x)2+32,所以x=5.
所以DE的长为5.
19.解析 (1)观察给出的勾股数得,斜边长与较长直角边长的差是1,即c-b=1.
∵a=19,a2+b2=c2,∴192+b2=(b+1)2,
∴b=180,∴c=181.
(2)由(1)知c-b=1,∵a=2n+1,∴(2n+1)2+b2=c2,
∴c2-b2=(2n+1)2,即(c+b)(c-b)=(2n+1)2,
∴b+c=(2n+1)2,又c=b+1,∴2b+1=(2n+1)2,
∴b=2n2+2n,∴c=2n2+2n+1.
(3)15,111,112不是一组勾股数.
理由:由(2)知,2n+1,2n2+2n,2n2+2n+1为一组勾股数,
当2n+1=15时,n=7,但2n2+2n=2×72+2×7=112≠111,2n2+2n+1=113≠112,∴15,111,112不是一组勾股数.
20.解析 由题图可得正方形ACFD的面积=四边形ABFE的面积=Rt△BAE和Rt△BFE的面积之和,即S正方形ACFD=S△BAE+S△BFE,
∴b2=c2+,整理,得a2+b2=c2.
_21?????????è?????(www.21cnjy.com)_
