北师大版八年级数学上册一课一练试题 :6.4《数据的离散程度 》习题1(Word版 含答案)
文档属性
| 名称 | 北师大版八年级数学上册一课一练试题 :6.4《数据的离散程度 》习题1(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 989.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 10:44:05 | ||
图片预览



文档简介
6.4《数据的离散程度
》习题1
一、填空题
1.某次模拟训练中,甲、乙两名射击运动员各射击了发子弹,随后教练员将他们的成绩绘制成了如图的折线统计图,由统计图计算可得(环),进一步分析,两人中成绩更加稳定的是________________(填“甲”或“乙”).
2.已知一组数据:3,3,4,5,5,则它的方差为________.
3.一组数据4,5,6,x的极差是5,则x=_____.
4.若一组数据、、、的方差是2,则、、、的方差是______.
二、选择题
1.小明在参加区运动会前刻苦进行100米跑训练,老师对他10次的训练成绩进行统计分析,判断他的成绩是否稳定,则老师需要知道他这10次成绩的(
)
A.众数
B.方差
C.平均数
D.频数
2.某体校要从四名射击选手中选拔一名选手参加省体育运动会,选拔赛中每名选手连续射靶次,他们各自的平均成绩及其方差如下表所示:
甲
乙
丙
丁
(环)
如果要选出一名成绩高且发挥稳定的选手参赛,则应选择的选手是(
)
A.甲
B.乙
C.丙
D.丁
3.在2,5,3,7,2,6,2,1这组数据中插入一个任意数x,则一定不会改变的是(
)
A.标准差
B.中位数
C.平均数
D.众数
4.甲、乙、丙、丁四人进行射击测试,每人次射击成绩的平均数均是环,方差分别为,,,,则成绩最稳定的是(
)
A.甲
B.乙
C.丙
D.丁
5.已知:一组数据-1,2,-1,5,3,4,关于这组数据,下列说法错误的是(
)
A.平均数是2
B.众数和中位数分别是-1和2.5
C.方差是16
D.标准差是
6.八年级一,二班的同学在一次数学测验中的成绩统计情况如下表:
班级
参加人数
中位数
平均数
方差
一
二
某同学分析后得到如下结论:①一,二班学生成绩平均水平相同;②二班优生人数不少于一班(优生线分);③一班学生的成绩相对稳定.其中正确的是( )
A.②③
B.①②
C.①③
D.①②③
7.学校篮球队名场上队员的身高分别为:,,,,(单位:).增加一名身高为的成员后,现篮球队成员的身高与原来相比,下列说法正确的是(
)
A.方差不变
B.方差变大
C.方差变小
D.不能确定
8.甲和乙一起练习射击,第一轮10枪打完后两人的成绩如图所示.设他们这10次射击成绩的方差为、,下列关系正确的是(
)
A.
B.
C.
D.无法确定
9.一组数据1,2,2,3,5,将这组数据中的每一个数都加上,得到一组新数据,,,,,这两组数据的以下统计量相等的是(
)
A.平均数
B.众数
C.中位数
D.方差
10.疫情无情人有情,爱心捐款传真情.新冠肺炎疫情发生后,某班学生积极参加献爱心活动,该班40名学生的捐款统计情况如下表,关于捐款金额,下列说法错误的是(
)
金额/元
10
20
30
50
100
人数
2
18
10
8
2
A.平均数为32元
B.众数为20元
C.中位数为20元
D.方差为386
11.一组数据1,2,1,4,2的方差为(
)
A.1
B.1.2
C.1.5
D.1.6
12.某班级开展“好书伴成长”读书活动,统计了1至7月份该班同学每月阅读课外书的数量,绘制了折线统计图,下列说法正确的是( )
A.每月阅读课外书本数的众数是45
B.每月阅读课外书本数的中位数是58
C.从2到6月份阅读课外书的本数逐月下降
D.从1到7月份每月阅读课外书本数的最大值比最小值多45
13.2020年春节新冠肺炎袭扰中国,习近平指挥全民战“疫”,全世界各国积极响应,纷纷捐款捐物献策,今年春节不串门,武汉加油显精神.科研人员夜以继日寻良药,白衣天使逆行而上抗病魔.某兴趣小组了解到一组关于新冠肺炎治愈的数据,从1月30日到2月4日的治愈人数不断增长,每日增长率分别为,,,,,.关于这组数据,下列说法正确的是(
)
A.方差是0
B.众数是
C.平均数是
D.中位数是
14.某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试因此计算其他39人的平均分为90分,方差s2=41.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是(
)
A.平均分不变,方差变大
B.平均分不变,方差变小
C.平均分和方差都不变
D.平均分和方差都改变
三、解答题
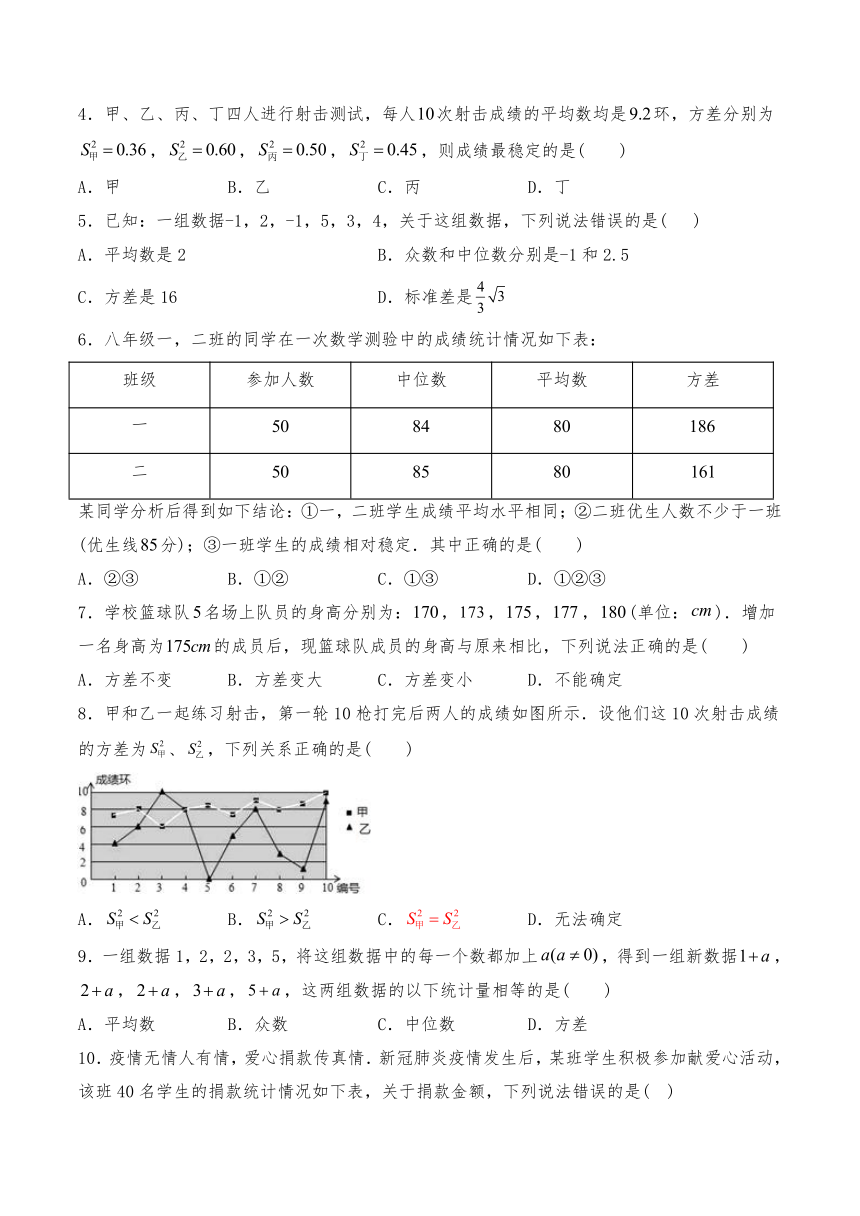
1.甲、乙两支篮球队在集训期内进行了五场比赛,将比赛成绩进行统计后,绘制成如图1、图2的统计图.(1)已知甲队五场比赛成绩的平均分=90分,请你计算乙队五场比赛成绩的平均分;(2)就这五场比赛,分别计算两队成绩的极差;(3)如果从甲、乙两队中选派一支球队参加篮球锦标赛,根据上述统计情况,试从平均分、折线的走势、获胜场数和极差四个方面分别进行简要分析,你认为选派哪支球队参赛更能取得好成绩?
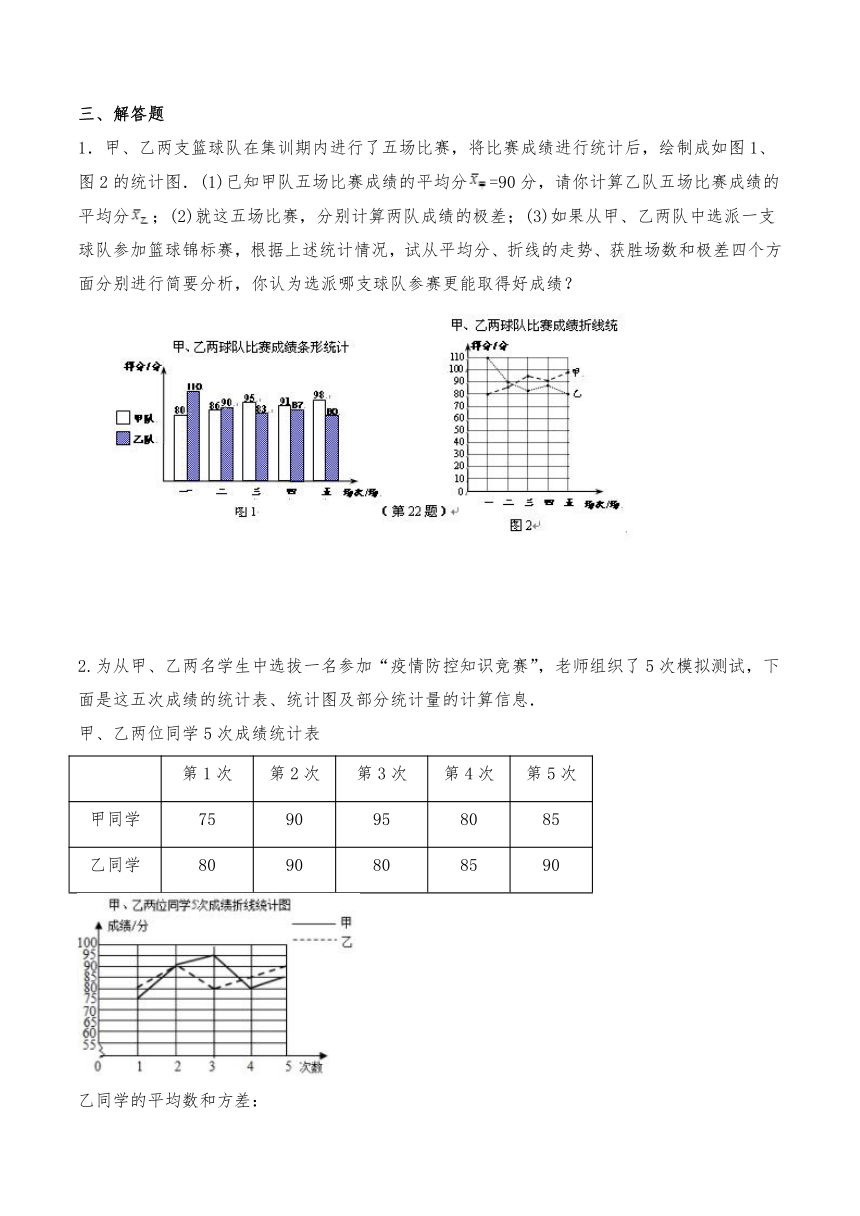
2.为从甲、乙两名学生中选拔一名参加“疫情防控知识竞赛”,老师组织了5次模拟测试,下面是这五次成绩的统计表、统计图及部分统计量的计算信息.
甲、乙两位同学5次成绩统计表
第1次
第2次
第3次
第4次
第5次
甲同学
75
90
95
80
85
乙同学
80
90
80
85
90
乙同学的平均数和方差:
(1)补充完整折线统计图;
(2)求甲同学成绩的方差;
(3)请你根据已学的统计知识,判断谁更适合参加竞赛?并说明理由.
3.为参加市里举行的“汉字听写”大赛,某校八年级两个班各选派10名学生参加学校举行的预赛,各参赛选手的成绩(满分100分)如下):
A班:88,91,92,93,93,93,94,98,98,100.
B班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级
平均分
中位数
众数
方差
班
94
12
班
95
93
8.4
(1)直接写出表中、、的值!
(2)嘉嘉说:“我也去参加比赛了,得了93分,在我们班是中等水平.”你认为嘉嘉是______班学生.(填“”或“”)
(3)依据数据分析表,有人说最高分在班,应选班去市里参加比赛,但也有人说选班更好,请至少写出两个应该选择班的理由.
4.某校要从小明和小亮两名运动员中挑出一人参加立定跳远比赛,学校记录了二人在最近的6次立定跳远选拔赛中的成绩(单位:cm),并进行整理、描述和分析,下面给出了部分信息.
a.如图:
b.小亮最近6次选拔赛成绩如下:
250,254,260,271,255,240
c.小明和小亮最近6次选拔赛成绩的平均数、中位数、方差如下:
平均数(cm)
中位数(cm)
方差()
小明
252.5
129.7
小亮
255
88.7
根据以上信息,回答下列问题:
(1)________,________;
(2)历届比赛表明:成绩达到266cm就有可能夺冠,成绩达到270cm就能打破纪录(积分加倍),根据这6次选拔赛成绩,你认为应选________(填“小明”或“小亮”)参加这项比赛,并说明理由,至少从两个不同的角度说明推断的合理性.
5.如图为A,B两家网店去年上半年的月销售额折线图.
(1)分别写出两家网店1﹣6月的月销售额的中位数.
(2)已知两家网店1﹣6月的月平均销售额都是28万元,你认为哪家网店的月销售额比较稳定?请说明理由.
(3)根据此统计图及相关数据,你认为哪家网店经营状况较好?请简述理由.
6.距离中考体考时间越来越近,年级想了解初三年级1512名学生周末在家体育锻炼的情况,在初三年级随机抽取了18名男生和18名女生,对他们周末在家的锻炼时间进行了调查,并收集得到了以下数据(单位:分钟)
男生:28,30,32,46,68,39,80,70,66,57,70,95,100,58,69,88,99,105
女生:36,48,78,99,56,62,35,109,29,88,88,69,73,55,90,98,69,72
统计数据,并制作了如下统计表:
时间
男生
2
4
女生
1
5
9
3
分析数据:两组数据的极差、平均数、中位数、众数如表所示
极差
平均数
中位数
众数
方差
男生
77
66.7
70
617.3
女生
69.7
70.5
547.2
(1)请将上面的表格补充完整: , , , , ;
(2)已知该年级男女生人数差不多,根据调查的数据,估计初三年级周末在家锻炼的时间在90分钟以上(不包含90分钟)的同学约有多少人?
(3)体育老师看了表格数据后认为初三年级的女生周末锻炼做得比男生好,请你结合统计数据,写出两条支持体育老师观点的理由.
7.(1)已知数据99,97,96,98,95,这组数据画成折线图(如图1).将这组数据的每一个数都减去97,得到一组新数据,在图2中将这组数据画成折线图,则新数据的方差
原数据的方差(填“大于”、“等于”、“小于”)
(2)已知数据5,3,2,4,1,这组数据画成折线图(如图3).将这组数据的每一个数都乘以2,得到一组新数据,在图4中将这组数据画成折线图,则新数据的方差
原数据的方差(填“大于”、“等于”、“小于”).
(3)已知甲组数据的平均数为,方差为.将这组数据的每一个数都乘以3再加上1,得到乙组数据,它们的平均数为,方差为,比较与的大小,并说明理由.
8.树叶有关的问题:
如图,一片树叶的长是指沿叶脉方向量出的最长部分的长度(不含叶柄)树叶的宽是指沿与主叶脉垂直方向量出的最宽处的长度,树叶的长宽比是指树叶的长与树叶的宽的比值.
某同学在校园内随机收集了树、树、树三棵的树叶各片,通过测量得到这些树叶的长(单位:),宽(单位:)的数据,计算长宽比,整理如下:
表1
树、树、树树叶的长宽比统计表
树树叶的长宽比
树树叶的长宽比
树树叶的长宽比
表2树、树、树树叶的长宽比的平均数、中位数、众数、方差统计表
平均数
中位数
众数
方差
树树叶的长宽比
树树叶的长宽比
树树叶的长宽比
树、树、树树叶的长随宽变化的情况(图1)
解决下列问题:
(1)写出表2中,的值.
(2)①小张同学说:“根据以上信息,我能判断树树叶的长、宽近似相等.”
②小李同学说:“从树叶的长宽比的平均数来看,我认为,下图的树叶是树的树叶.”
请你判断上面两位同学的说法中,谁的说法是合理的,谁的说法是不合理的,并给出你的理由.
(3)现有一片长,宽的树叶,请将该树叶的数用“★”表示在图1中,判断这片树叶更可能来自于、、中的哪棵树?并给出你的理由.
答案
一、填空题
1.甲
2..
3.1或9.
4.2.
二、选择题
1.B.2.A.3.D.4.A.5.C
6.B
7.C.8.A.9.D.10.C.11.B.12.B.13.C.14.B
三、解答题
1.解:(1)=90(分);
(2)甲队成绩的极差是18分,
乙队成绩的极差是30分;
(3)从平均分看,两队的平均分相同,实力大体相当;
从折线的走势看,甲队比赛成绩呈上升趋势,而乙队比赛成绩呈下降趋势;
从获胜场数看,甲队胜三场,乙队胜两场,甲队成绩较好;
从极差看,甲队比赛成绩比乙队比赛成绩波动小,甲队成绩较稳定.
综上,选派甲队参赛更能取得好成绩.
2.解:(1)如图即为补充完整的折线统计图;
(2)甲同学的平均数和方差:
,
,
答:甲同学成绩的方差为50;
(3)乙同学更适合参加竞赛,理由如下:
因为甲、乙两人5次测试成绩的平均数相同,但乙的方差比甲小,说明乙的成绩更稳定,所以乙同学更适合参加竞赛.
3.解:(1)由题意得:
A班的中位数为:;众数为:93;
B班的中位数为:;
故答案为:,,;
(2)由题意可得:嘉嘉是A班的学生;
故答案为A;
(3)由题意得:
①B班的平均分比A班高,
②B班的成绩波动也比A班稳定;
∴应该选择B班.
4.解:(1)中位数m=
=254.5,n==252.
故答案为254.5,252.
(2)选:小亮.
理由:小亮的平均数比小明大,方差较小.
故答案为小亮的平均数比小明大,方差较小.
5.解:(1)A店销售额按从小到大依次排列为17,22,28,30,32,39;中位数为×(28+30)=29(万元);
B店销售额从小到大依次排列为16,20,26,28,38,40;中位数为×(26+28)=27(万元).
(2)=×[(17﹣28)2+(22﹣28)2+(28﹣28)2+(30﹣28)2+(32﹣28)2+(39﹣28)2]=;
=×[(16﹣28)2+(20﹣28)2+(26﹣28)2+(28﹣28)2+(38﹣28)2+(40﹣28)2]=76,
∵<;
∴A网店的月销售额比较稳定;
(3)在统计图中,虽然B网站走势较好,并且A网站和B网站月销售额平均数相等,但A网站的中位数大于B网站的中位数,并且A网站的月销售额比较稳定,所以
A网站经营较好.
6.(1)∵周末男生在家锻炼时间在的有5人,在的有7人,
∴m=5,n=7,
∵男生的锻炼时间从小到大排序后,排在中间的两个数为69和70,
∴b=68.5,
∵109-29=80,
∴a=80,
∵女生的锻炼时间中,88和69都出现了两次,
∴c=88或69.
故答案是:5,7,80,68.5,88或69;
(2)据表格,可得锻炼时间在90分钟以上的男生有4人,女生有3人,
(人),
答:初三年级锻炼时间在90分钟以上的同学有294人;
(3)理由一:因为,所以女生锻炼时间的平均时间更长,因此女生周末做得更好.
理由二:因为,所以锻炼时间排序后在中间位置的女生比男生更好,因此女生周末做得更好.
7.解:(1)新数据画成的折线图如下所示:
原来数据的平均数,
原来数据的方差,
新数据的平均数,
新数据的方差,
故新数据的方程等于原来数据的方程,
故答案为:等于;
(2)新数据画成的折线图如下所示:
新数据的平均数,
新数据的方差,
故新数据的方差大于原来数据的方差,
故答案为:大于;
(3)
=
=
=
=
故答案为:≥.
8.(1)将树树叶的长宽比按从小到大的排列为:
,,,,,,,,,.
中位数为:
众数是:,
,.
(2)①说法合理:平均数和中位数均为,众数为.
树树叶的长宽比近似,即长,宽近似相等;
②不合理:下树树叶的长明显大于宽,从长宽比的平均数看,是树树叶
(3)长:,宽,
长宽比为:
更接近树长宽比的平均数
这片树叶更可能来自于树.
树、树、树树叶的长随宽变化的情况
》习题1
一、填空题
1.某次模拟训练中,甲、乙两名射击运动员各射击了发子弹,随后教练员将他们的成绩绘制成了如图的折线统计图,由统计图计算可得(环),进一步分析,两人中成绩更加稳定的是________________(填“甲”或“乙”).
2.已知一组数据:3,3,4,5,5,则它的方差为________.
3.一组数据4,5,6,x的极差是5,则x=_____.
4.若一组数据、、、的方差是2,则、、、的方差是______.
二、选择题
1.小明在参加区运动会前刻苦进行100米跑训练,老师对他10次的训练成绩进行统计分析,判断他的成绩是否稳定,则老师需要知道他这10次成绩的(
)
A.众数
B.方差
C.平均数
D.频数
2.某体校要从四名射击选手中选拔一名选手参加省体育运动会,选拔赛中每名选手连续射靶次,他们各自的平均成绩及其方差如下表所示:
甲
乙
丙
丁
(环)
如果要选出一名成绩高且发挥稳定的选手参赛,则应选择的选手是(
)
A.甲
B.乙
C.丙
D.丁
3.在2,5,3,7,2,6,2,1这组数据中插入一个任意数x,则一定不会改变的是(
)
A.标准差
B.中位数
C.平均数
D.众数
4.甲、乙、丙、丁四人进行射击测试,每人次射击成绩的平均数均是环,方差分别为,,,,则成绩最稳定的是(
)
A.甲
B.乙
C.丙
D.丁
5.已知:一组数据-1,2,-1,5,3,4,关于这组数据,下列说法错误的是(
)
A.平均数是2
B.众数和中位数分别是-1和2.5
C.方差是16
D.标准差是
6.八年级一,二班的同学在一次数学测验中的成绩统计情况如下表:
班级
参加人数
中位数
平均数
方差
一
二
某同学分析后得到如下结论:①一,二班学生成绩平均水平相同;②二班优生人数不少于一班(优生线分);③一班学生的成绩相对稳定.其中正确的是( )
A.②③
B.①②
C.①③
D.①②③
7.学校篮球队名场上队员的身高分别为:,,,,(单位:).增加一名身高为的成员后,现篮球队成员的身高与原来相比,下列说法正确的是(
)
A.方差不变
B.方差变大
C.方差变小
D.不能确定
8.甲和乙一起练习射击,第一轮10枪打完后两人的成绩如图所示.设他们这10次射击成绩的方差为、,下列关系正确的是(
)
A.
B.
C.
D.无法确定
9.一组数据1,2,2,3,5,将这组数据中的每一个数都加上,得到一组新数据,,,,,这两组数据的以下统计量相等的是(
)
A.平均数
B.众数
C.中位数
D.方差
10.疫情无情人有情,爱心捐款传真情.新冠肺炎疫情发生后,某班学生积极参加献爱心活动,该班40名学生的捐款统计情况如下表,关于捐款金额,下列说法错误的是(
)
金额/元
10
20
30
50
100
人数
2
18
10
8
2
A.平均数为32元
B.众数为20元
C.中位数为20元
D.方差为386
11.一组数据1,2,1,4,2的方差为(
)
A.1
B.1.2
C.1.5
D.1.6
12.某班级开展“好书伴成长”读书活动,统计了1至7月份该班同学每月阅读课外书的数量,绘制了折线统计图,下列说法正确的是( )
A.每月阅读课外书本数的众数是45
B.每月阅读课外书本数的中位数是58
C.从2到6月份阅读课外书的本数逐月下降
D.从1到7月份每月阅读课外书本数的最大值比最小值多45
13.2020年春节新冠肺炎袭扰中国,习近平指挥全民战“疫”,全世界各国积极响应,纷纷捐款捐物献策,今年春节不串门,武汉加油显精神.科研人员夜以继日寻良药,白衣天使逆行而上抗病魔.某兴趣小组了解到一组关于新冠肺炎治愈的数据,从1月30日到2月4日的治愈人数不断增长,每日增长率分别为,,,,,.关于这组数据,下列说法正确的是(
)
A.方差是0
B.众数是
C.平均数是
D.中位数是
14.某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试因此计算其他39人的平均分为90分,方差s2=41.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是(
)
A.平均分不变,方差变大
B.平均分不变,方差变小
C.平均分和方差都不变
D.平均分和方差都改变
三、解答题
1.甲、乙两支篮球队在集训期内进行了五场比赛,将比赛成绩进行统计后,绘制成如图1、图2的统计图.(1)已知甲队五场比赛成绩的平均分=90分,请你计算乙队五场比赛成绩的平均分;(2)就这五场比赛,分别计算两队成绩的极差;(3)如果从甲、乙两队中选派一支球队参加篮球锦标赛,根据上述统计情况,试从平均分、折线的走势、获胜场数和极差四个方面分别进行简要分析,你认为选派哪支球队参赛更能取得好成绩?
2.为从甲、乙两名学生中选拔一名参加“疫情防控知识竞赛”,老师组织了5次模拟测试,下面是这五次成绩的统计表、统计图及部分统计量的计算信息.
甲、乙两位同学5次成绩统计表
第1次
第2次
第3次
第4次
第5次
甲同学
75
90
95
80
85
乙同学
80
90
80
85
90
乙同学的平均数和方差:
(1)补充完整折线统计图;
(2)求甲同学成绩的方差;
(3)请你根据已学的统计知识,判断谁更适合参加竞赛?并说明理由.
3.为参加市里举行的“汉字听写”大赛,某校八年级两个班各选派10名学生参加学校举行的预赛,各参赛选手的成绩(满分100分)如下):
A班:88,91,92,93,93,93,94,98,98,100.
B班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级
平均分
中位数
众数
方差
班
94
12
班
95
93
8.4
(1)直接写出表中、、的值!
(2)嘉嘉说:“我也去参加比赛了,得了93分,在我们班是中等水平.”你认为嘉嘉是______班学生.(填“”或“”)
(3)依据数据分析表,有人说最高分在班,应选班去市里参加比赛,但也有人说选班更好,请至少写出两个应该选择班的理由.
4.某校要从小明和小亮两名运动员中挑出一人参加立定跳远比赛,学校记录了二人在最近的6次立定跳远选拔赛中的成绩(单位:cm),并进行整理、描述和分析,下面给出了部分信息.
a.如图:
b.小亮最近6次选拔赛成绩如下:
250,254,260,271,255,240
c.小明和小亮最近6次选拔赛成绩的平均数、中位数、方差如下:
平均数(cm)
中位数(cm)
方差()
小明
252.5
129.7
小亮
255
88.7
根据以上信息,回答下列问题:
(1)________,________;
(2)历届比赛表明:成绩达到266cm就有可能夺冠,成绩达到270cm就能打破纪录(积分加倍),根据这6次选拔赛成绩,你认为应选________(填“小明”或“小亮”)参加这项比赛,并说明理由,至少从两个不同的角度说明推断的合理性.
5.如图为A,B两家网店去年上半年的月销售额折线图.
(1)分别写出两家网店1﹣6月的月销售额的中位数.
(2)已知两家网店1﹣6月的月平均销售额都是28万元,你认为哪家网店的月销售额比较稳定?请说明理由.
(3)根据此统计图及相关数据,你认为哪家网店经营状况较好?请简述理由.
6.距离中考体考时间越来越近,年级想了解初三年级1512名学生周末在家体育锻炼的情况,在初三年级随机抽取了18名男生和18名女生,对他们周末在家的锻炼时间进行了调查,并收集得到了以下数据(单位:分钟)
男生:28,30,32,46,68,39,80,70,66,57,70,95,100,58,69,88,99,105
女生:36,48,78,99,56,62,35,109,29,88,88,69,73,55,90,98,69,72
统计数据,并制作了如下统计表:
时间
男生
2
4
女生
1
5
9
3
分析数据:两组数据的极差、平均数、中位数、众数如表所示
极差
平均数
中位数
众数
方差
男生
77
66.7
70
617.3
女生
69.7
70.5
547.2
(1)请将上面的表格补充完整: , , , , ;
(2)已知该年级男女生人数差不多,根据调查的数据,估计初三年级周末在家锻炼的时间在90分钟以上(不包含90分钟)的同学约有多少人?
(3)体育老师看了表格数据后认为初三年级的女生周末锻炼做得比男生好,请你结合统计数据,写出两条支持体育老师观点的理由.
7.(1)已知数据99,97,96,98,95,这组数据画成折线图(如图1).将这组数据的每一个数都减去97,得到一组新数据,在图2中将这组数据画成折线图,则新数据的方差
原数据的方差(填“大于”、“等于”、“小于”)
(2)已知数据5,3,2,4,1,这组数据画成折线图(如图3).将这组数据的每一个数都乘以2,得到一组新数据,在图4中将这组数据画成折线图,则新数据的方差
原数据的方差(填“大于”、“等于”、“小于”).
(3)已知甲组数据的平均数为,方差为.将这组数据的每一个数都乘以3再加上1,得到乙组数据,它们的平均数为,方差为,比较与的大小,并说明理由.
8.树叶有关的问题:
如图,一片树叶的长是指沿叶脉方向量出的最长部分的长度(不含叶柄)树叶的宽是指沿与主叶脉垂直方向量出的最宽处的长度,树叶的长宽比是指树叶的长与树叶的宽的比值.
某同学在校园内随机收集了树、树、树三棵的树叶各片,通过测量得到这些树叶的长(单位:),宽(单位:)的数据,计算长宽比,整理如下:
表1
树、树、树树叶的长宽比统计表
树树叶的长宽比
树树叶的长宽比
树树叶的长宽比
表2树、树、树树叶的长宽比的平均数、中位数、众数、方差统计表
平均数
中位数
众数
方差
树树叶的长宽比
树树叶的长宽比
树树叶的长宽比
树、树、树树叶的长随宽变化的情况(图1)
解决下列问题:
(1)写出表2中,的值.
(2)①小张同学说:“根据以上信息,我能判断树树叶的长、宽近似相等.”
②小李同学说:“从树叶的长宽比的平均数来看,我认为,下图的树叶是树的树叶.”
请你判断上面两位同学的说法中,谁的说法是合理的,谁的说法是不合理的,并给出你的理由.
(3)现有一片长,宽的树叶,请将该树叶的数用“★”表示在图1中,判断这片树叶更可能来自于、、中的哪棵树?并给出你的理由.
答案
一、填空题
1.甲
2..
3.1或9.
4.2.
二、选择题
1.B.2.A.3.D.4.A.5.C
6.B
7.C.8.A.9.D.10.C.11.B.12.B.13.C.14.B
三、解答题
1.解:(1)=90(分);
(2)甲队成绩的极差是18分,
乙队成绩的极差是30分;
(3)从平均分看,两队的平均分相同,实力大体相当;
从折线的走势看,甲队比赛成绩呈上升趋势,而乙队比赛成绩呈下降趋势;
从获胜场数看,甲队胜三场,乙队胜两场,甲队成绩较好;
从极差看,甲队比赛成绩比乙队比赛成绩波动小,甲队成绩较稳定.
综上,选派甲队参赛更能取得好成绩.
2.解:(1)如图即为补充完整的折线统计图;
(2)甲同学的平均数和方差:
,
,
答:甲同学成绩的方差为50;
(3)乙同学更适合参加竞赛,理由如下:
因为甲、乙两人5次测试成绩的平均数相同,但乙的方差比甲小,说明乙的成绩更稳定,所以乙同学更适合参加竞赛.
3.解:(1)由题意得:
A班的中位数为:;众数为:93;
B班的中位数为:;
故答案为:,,;
(2)由题意可得:嘉嘉是A班的学生;
故答案为A;
(3)由题意得:
①B班的平均分比A班高,
②B班的成绩波动也比A班稳定;
∴应该选择B班.
4.解:(1)中位数m=
=254.5,n==252.
故答案为254.5,252.
(2)选:小亮.
理由:小亮的平均数比小明大,方差较小.
故答案为小亮的平均数比小明大,方差较小.
5.解:(1)A店销售额按从小到大依次排列为17,22,28,30,32,39;中位数为×(28+30)=29(万元);
B店销售额从小到大依次排列为16,20,26,28,38,40;中位数为×(26+28)=27(万元).
(2)=×[(17﹣28)2+(22﹣28)2+(28﹣28)2+(30﹣28)2+(32﹣28)2+(39﹣28)2]=;
=×[(16﹣28)2+(20﹣28)2+(26﹣28)2+(28﹣28)2+(38﹣28)2+(40﹣28)2]=76,
∵<;
∴A网店的月销售额比较稳定;
(3)在统计图中,虽然B网站走势较好,并且A网站和B网站月销售额平均数相等,但A网站的中位数大于B网站的中位数,并且A网站的月销售额比较稳定,所以
A网站经营较好.
6.(1)∵周末男生在家锻炼时间在的有5人,在的有7人,
∴m=5,n=7,
∵男生的锻炼时间从小到大排序后,排在中间的两个数为69和70,
∴b=68.5,
∵109-29=80,
∴a=80,
∵女生的锻炼时间中,88和69都出现了两次,
∴c=88或69.
故答案是:5,7,80,68.5,88或69;
(2)据表格,可得锻炼时间在90分钟以上的男生有4人,女生有3人,
(人),
答:初三年级锻炼时间在90分钟以上的同学有294人;
(3)理由一:因为,所以女生锻炼时间的平均时间更长,因此女生周末做得更好.
理由二:因为,所以锻炼时间排序后在中间位置的女生比男生更好,因此女生周末做得更好.
7.解:(1)新数据画成的折线图如下所示:
原来数据的平均数,
原来数据的方差,
新数据的平均数,
新数据的方差,
故新数据的方程等于原来数据的方程,
故答案为:等于;
(2)新数据画成的折线图如下所示:
新数据的平均数,
新数据的方差,
故新数据的方差大于原来数据的方差,
故答案为:大于;
(3)
=
=
=
=
故答案为:≥.
8.(1)将树树叶的长宽比按从小到大的排列为:
,,,,,,,,,.
中位数为:
众数是:,
,.
(2)①说法合理:平均数和中位数均为,众数为.
树树叶的长宽比近似,即长,宽近似相等;
②不合理:下树树叶的长明显大于宽,从长宽比的平均数看,是树树叶
(3)长:,宽,
长宽比为:
更接近树长宽比的平均数
这片树叶更可能来自于树.
树、树、树树叶的长随宽变化的情况
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
