北师大版八年级数学上册 6.4《数据的离散程度 》一课一练(word含答案)
文档属性
| 名称 | 北师大版八年级数学上册 6.4《数据的离散程度 》一课一练(word含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 439.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 11:39:51 | ||
图片预览




文档简介
6.4《数据的离散程度
》习题2
一、选择题
1.在学校数学竞赛中,某校名学生参赛成绩统计如图所示,对于这名学生的参赛成绩,下列说法中错误的是( )
A.众数是
B.中位数是
C.平均数是
D.极差是
2.已知一组数据:5,5,6,7,4,则这组数据的极差与众数分别是( )
A.5,3
B.3,2
C.3,5
D.2,3
3.一组数据为5,6,7,7,10,10,某同学在抄题的时候,误将其中的一个10抄成了16,那么该同学所抄的数据和原数据相比,不变的统计量是(
)
A.极差
B.平均数
C.中位数
D.众数
4.为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元)
5
10
20
50
100
人数(单位:个)
2
4
5
3
1
关于这15名同学所捐款的数额,下列说法正确的是(
)
A.众数是100
B.平均数是30
C.极差是20
D.中位数是20
5.某射击运动员在训练中射击了10次,成绩如图所示:下列结论正确的是(
)
A.众数是8,中位数是8
B.众数是8,中位数是8.5
C.平均数是8.2,方差是1.2
D.平均数是8,方差是1.2
6.如果数据,,,的方差是,则另一组数据,,,的方差是(
)
A.
B.
C.
D.
7.某小区超市实行消费积分制,该小区位住户年在该超市的积分分别为分、分、分.则这三位住户年在超市积分的平均数和方差分别是(
)
A.分、
B.分、
C.分、
D.分、
8.为了解新冠肺炎疫情防控期间,学生居家进行“线上学习”情况,某班进行了某学科单元基础知识“线上测试”,其中抽查的10名学生的成绩如图所示,对于这10名学生的测试成绩,下列说法正确的是(
)
A.中位数是95分
B.众数是90分
C.平均数是95分
D.方差是15
9.某校7名学生在某次测量体温(单位:℃)时得到如下数据:36.3,36.4,36.5,36.7,36.6,36.5,36.5,对这组数据描述正确的是( )
A.众数是36.5
B.中位数是36.7
C.平均数是36.6
D.方差是0.4
10.点点同学对数据26,36,46,5,52进行统计分析,发现其中一个两位数的个位数字被黑水涂污看不到了,则计算结果与被涂污数字无关的是( )
A.平均数
B.中位数
C.方差
D.标准差
11.测试五位学生的“立定跳远”成绩,得到5个互不相同的数据,在统计时出现一处错误,将最低成绩写得更低了,计算不受影响的是(
)
A.方差
B.标准差
C.平均数
D.中位数
12.某同学对数据28,32,36,42,5,54进行统计分析时,发现其中一个两位数的个位数字被墨水涂污看不清楚了,但计算结果与被涂污的数字无关的是(
)
A.平均数
B.中位数
C.方差
D.标准差
13.已知一组数据的方差是3,则这组数据的标准差是(
)
A.9
B.3
C.
D.
14.某市疾控中心在对10名某传染病确诊病人的流行病史的调查中发现,这10人的潜伏期分别为:5,5,5,7,7,8,8,9,11,14(单位:天),则下列关于这组潜伏期数据的说法中不正确的是( )
A.众数是5天
B.中位数是7.5天
C.平均数是7.9天
D.标准差是2.5天
15.已知数据1,2,3,3,4,5,则下列关于这组数据的说法,错误的是( )
A.平均数是3
B.中位数和众数都是3
C.方差为10
D.标准差是
二、填空题
1.有一组数据如下:2,3,a,5,6,它们的平均数是4,则这组数据的极差是______
2.贝贝在练习“投掷铅球”项目活动中进行了5次测试,测试成绩(单位:分)如下:10,7,9,4,10.则贝贝5次成绩的极差是_____.
3.某班体育委员统计了全班45名同学一周的体育锻炼时间(单位:小时),并绘制了如图的折线统计图,这组数据的中位数是_____,极差是_____,平均数是_____.
4.某次对中学生身高的抽样调查中测得5个同学的身高如下(单位:cm):172,171,175,174,178,则这组数据的方差为________.
5.已知一组数据:x1,x2,x3,…,xn的平均数是2,方差是3,另一组数据:3x1﹣2,3x2﹣2,…3xn﹣2的方差是__________.
6.已知一组数据的方差是,那么另一组数据的方差是______.
7.已知一组数据的方差是则这组数据的标准差是_________.
8.一组数据,1,3,2,5,x的平均数为3,那么这组数据的标准差是______.
9.已知数据x1,x2,x3的平均数为a,方差为b,则数据2x1+3,2x2+3,2x3+3的标准差是_____.
三、解答题
1.已知A组数据如下:
0,1,-2,-1,0,-1,3.
(1)A组数据的中位数是
;
(2)求A组数据的方差;
(3)从A组数据中选取5个数据,记这5个数据为B组数据.
要求B组数据满足两个条件:①
它的平均数与A组数据的平均数相等;②
它的方差比A组数据的方差大.你选取的B组数据是
.
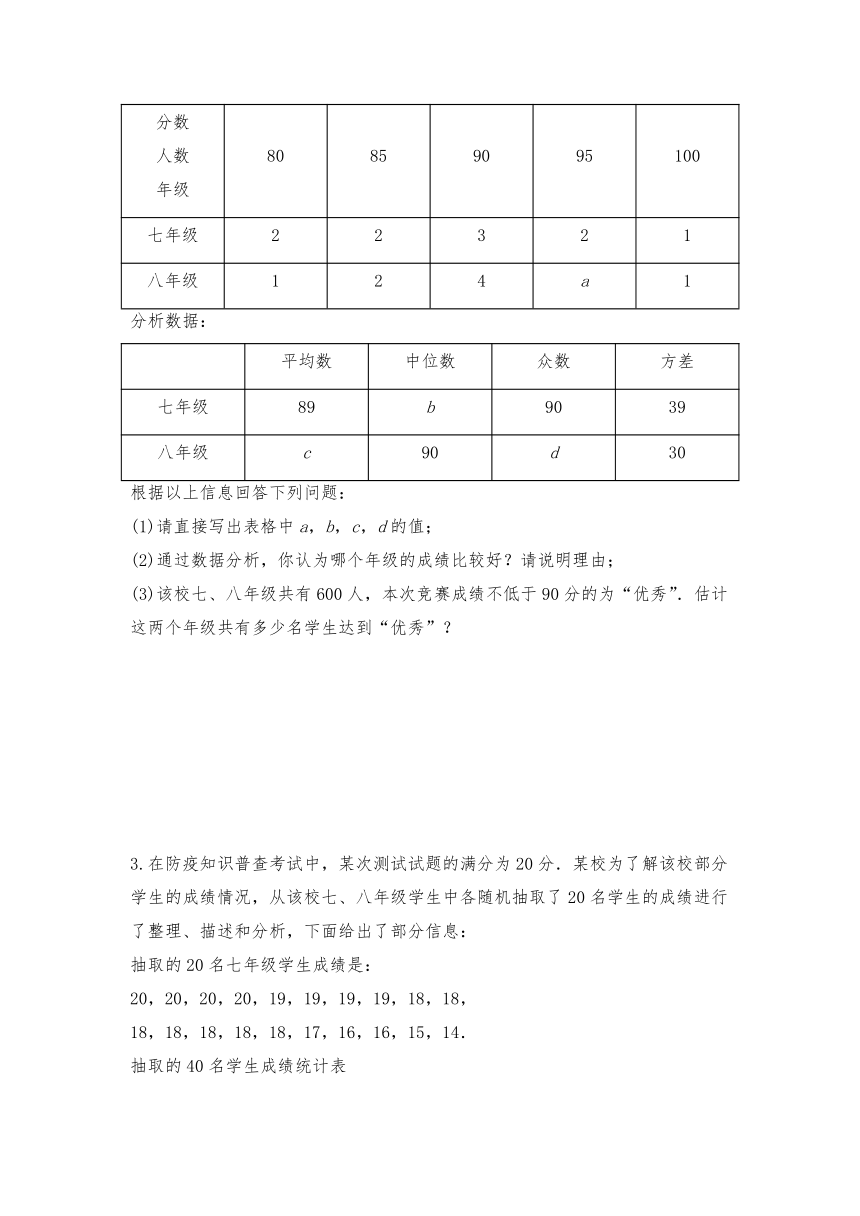
2.6月26日是“国际禁毒日”,某中学组织七、八年级全体学生开展了“禁毒知识”网上竞赛活动.为了解竞赛情况,从两个年级各随机抽取了10名同学的成绩(满分为100分),收集数据为:七年级90,95,95,80,90,80,85,90,85,100;八年级85,85,95,80,95,90,90,90,100,90.
整理数据:
分数
人数
年级
80
85
90
95
100
七年级
2
2
3
2
1
八年级
1
2
4
a
1
分析数据:
平均数
中位数
众数
方差
七年级
89
b
90
39
八年级
c
90
d
30
根据以上信息回答下列问题:
(1)请直接写出表格中a,b,c,d的值;
(2)通过数据分析,你认为哪个年级的成绩比较好?请说明理由;
(3)该校七、八年级共有600人,本次竞赛成绩不低于90分的为“优秀”.估计这两个年级共有多少名学生达到“优秀”?
3.在防疫知识普查考试中,某次测试试题的满分为20分.某校为了解该校部分学生的成绩情况,从该校七、八年级学生中各随机抽取了20名学生的成绩进行了整理、描述和分析,下面给出了部分信息:
抽取的20名七年级学生成绩是:
20,20,20,20,19,19,19,19,18,18,
18,18,18,18,18,17,16,16,15,14.
抽取的40名学生成绩统计表
七年级
八年级
平均分
18
18
众数
a
b
中位数
18
c
方差
2.7
2.7
根据以上信息,解答下列问题:
(1)直接写出上表中a,b,c的值;
(2)在这次测试中,你认为是七年级成绩好,还是八年级成绩好?请说明理由(一条理由即可);
(3)该校七、八年级共有学生1000人,估计此次测试成绩不低于19分的学生有多少人?
4.某校团委举办了一次“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上为合格,达到9分以上(含9分)为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如下.
(1)补充完成下列的成绩统计分析表:(写出方差的计算过程)
(2)甲组6分的人数比乙组6分的人数多_____%.
(3)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是________组学生;(填“甲”或“乙”)
(4)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
5.为了了解学生对“预防新型冠状病毒”知识的掌握情况,学校组织了一次线上知识培训,培训结束后进行测试,试题的满分为分.为了解学生的成绩情况,从七、八年级学生中各随机抽取了名学生的成绩进行了整理、描述和分析,下面给出了部分信息:
抽取的名七年级成绩是:
,,,,,,,,,,
,,,,,,,,,.
抽取的名八年级成绩折线统计图
抽取的名学生成绩统计表
性别
七年级
八年级
平均数
众数
中位数
方差
根据以上信息,解答下列问题:
(1)直接写出上表中,,的值:______,______,_______;
(2)在这次测试中,你认为是七年级成绩好,还是八年级成绩好?请说明理由;
6.某校八年级(1)班甲、乙两男生在5次引体向上测试中有效次数如下:
甲:8,8,7,8,9;乙:5,9,7,10,9;
甲乙两同学引体向上的平均数、众数、中位数、方差如下:
平均数
众数
中位数
方差
甲
8
b
8
0.4
乙
a
9
c
3.2
根据以上信息,回答下列问题:
(1)表格是a= ,b= ,c= .(填数值)
(2)体育老师根据这5次的成绩,决定选择甲同学代表班级参加年级引体向上比赛,选择甲的理由是
.班主任李老师根据去年比赛的成绩(至少9次才能获奖),决定选择乙同学代表班级参加年级引体向上比赛,选择乙的理由是
;
(3)如果乙同学再做一次引体向上,有效次数为8,那么乙同学6次引体向上成绩的平均数
,中位数
,方差
.(填“变大”、“变小”或“不变”)
7.某学校要调查学生关于“新冠肺炎”防治知识的了解情况,从七、八年级各随机抽取了10名学生进行测试(百分制),测试成绩整理、描述和分析如下:
(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100),七年级10名学生的成绩是:96,80,96,86,99,96,90,100,89,82.八年级10名学生的成绩在C组中的数据是:94,90,92.
七、八年级抽取的学生成绩统计表
年级
七年级
八年级
平均数
92
92
中位数
93
b
众数
c
100
方差
52
50.4
根据以上信息,解答下列问题:
(1)直接写出上述图表中a,b,c的值;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握“新冠肺炎”知识较好?请说明理由.
(3)该校七、八年级共1200人参加了此次调查活动,估计参加此次调查活动成绩优秀(x≥90)的学生人数是多少?
答案
一、选择题
1.B.2.C.3.C.4.D.5.A.6.C.7.B.8.B.9.A.
10.B
11.D.12.B
13.D
14.D
15.C.
二、填空题
1.4.
2.6.
3.9,4,9.
4.6.
5.27.
6..
7.2.
8..
9.2.
三、解答题
1.解:(1)把数据按从小到大排列如下:
最中间的数是:
所以这组数据的中位数是:
故答案为:
(2)这组数据的平均数为:
所以这组数据的方差为:
(3)组数据为:.
组数据的平均数为:
组数据的方差为:
由>,
所以组数据符合条件①②.
故答案为:.(答案不唯一)
2.解:(1)观察八年级95分的有2人,故a=2,
七年级的中位数为,故b=90,
八年级的平均数为:×(85+85+95+80+95+90+90+90+100+90)=90,故c=90,
八年级中90分的最多,故d=90;
(2)七、八年级学生成绩的中位数和众数相同,但八年级的平均成绩比七年级高,且从方差看,八年级学生成绩更整齐,综上,八年级的学生成绩好;
(3)∵600×=600×=390(人),
∴该校七、八年级这次竞赛达到优秀的有390人.
3.解:(1)七年级20名学生成绩的众数a=18,八年级成绩的众数b=19,中位数c==18.5;
(2)八年级的成绩好,
∵七年级与八年级成绩的平均分和方差相等,而八年级的中位数大于七年级的中位数,即八年级高分人数稍多,
∴八年级的成绩好;
(3)估计此次测试成绩不低于19分的学生有1000×=450(人).
4.解:(1)甲组:3,6,6,6,6,6,7,8,9,10,中位数为6(分);众数为6(分)
乙组:5,5,6,7,7,8,8,8,8,9,平均数=7.1(分),
S乙2==1.69(分2),众数为8(分);
故答案为:6,6,7.1,1.69,8;
(2)(5-1)÷1=4=400%;
故答案为400;
(3)因为甲组的中位数为6,所以7分在甲组排名属中游略偏上;
所以,小明是甲组学生;
故答案为:甲;
(4)乙组的平均数高于甲组;乙组的中位数高于甲组,所以乙组的成绩要好于甲组.
5.解:(1)七年级成绩的众数为18,
八年级成绩的众数为19,中位数为=18.5,
即a=18,b=19,c=18.5;
故答案为,,;
(2)解:八年级的成绩好
七年级与八年级成绩的平均分和方差相等,而八年级的中位数大于七年级的中位数,即八年级高分人数稍多,
八年级的成绩好.
6.(1),
因为甲中8共出现3次,次数最多,所以b=8
因为乙的有效次数中按顺序排列后处于中间位置的是9,所以中位数c=9;
故答案为a、b、c的值分别是8、8、9;
(2),
∴甲的方差较小,成绩比较稳定,
∴选择甲同学代表班级参加年级引体向上比赛;
∵乙的中位数是9,众数也是9,
∴获奖可能性较大,
∴根据去年比赛的成绩(至少9次才能获奖),决定选择乙同学代表班级参加年级引体向上比赛;
(3)∵原来的平均数是8,增加一次也是8,
∴平均数不变.
∵六次成绩排序为5,7,8,9,9,10,
∴处于中间位置的数为8,9,
∴中位数为
,
∴中位数变小.
后来的方差为,
∴方差变小.
7.解:(1)因为八年级组有人,组有人,组有人,
所以组有人,所以:
即
因为八年级学生成绩的分布:组有人,组有人,组有人,组有人,且成绩是按照从小到大的顺序排列的,所以八年级学生成绩的中位数落在组,而C组中的数据是:94,90,92,
按从小到大排列为:
所以第个,第个数据为:
所以中位数为:分,
因为七年级学生成绩中分有个,出现的次数最多,所以众数分,
故答案为:a=40,b=93,c=96.
(2)八年级掌握得更好.因为七八年级的平均数、中位数相同,
而八年级的众数比七年级高,说明八年级高分的同学更多;
八年级方差比七年级小,说明八年级两极分化差距小.
(3)由题意得:七年级成绩大于或等于分的有人,八年级成绩大于或等于分的有人
(人)
答:参加此次调查活动成绩优秀的学生人数约为780人.
》习题2
一、选择题
1.在学校数学竞赛中,某校名学生参赛成绩统计如图所示,对于这名学生的参赛成绩,下列说法中错误的是( )
A.众数是
B.中位数是
C.平均数是
D.极差是
2.已知一组数据:5,5,6,7,4,则这组数据的极差与众数分别是( )
A.5,3
B.3,2
C.3,5
D.2,3
3.一组数据为5,6,7,7,10,10,某同学在抄题的时候,误将其中的一个10抄成了16,那么该同学所抄的数据和原数据相比,不变的统计量是(
)
A.极差
B.平均数
C.中位数
D.众数
4.为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元)
5
10
20
50
100
人数(单位:个)
2
4
5
3
1
关于这15名同学所捐款的数额,下列说法正确的是(
)
A.众数是100
B.平均数是30
C.极差是20
D.中位数是20
5.某射击运动员在训练中射击了10次,成绩如图所示:下列结论正确的是(
)
A.众数是8,中位数是8
B.众数是8,中位数是8.5
C.平均数是8.2,方差是1.2
D.平均数是8,方差是1.2
6.如果数据,,,的方差是,则另一组数据,,,的方差是(
)
A.
B.
C.
D.
7.某小区超市实行消费积分制,该小区位住户年在该超市的积分分别为分、分、分.则这三位住户年在超市积分的平均数和方差分别是(
)
A.分、
B.分、
C.分、
D.分、
8.为了解新冠肺炎疫情防控期间,学生居家进行“线上学习”情况,某班进行了某学科单元基础知识“线上测试”,其中抽查的10名学生的成绩如图所示,对于这10名学生的测试成绩,下列说法正确的是(
)
A.中位数是95分
B.众数是90分
C.平均数是95分
D.方差是15
9.某校7名学生在某次测量体温(单位:℃)时得到如下数据:36.3,36.4,36.5,36.7,36.6,36.5,36.5,对这组数据描述正确的是( )
A.众数是36.5
B.中位数是36.7
C.平均数是36.6
D.方差是0.4
10.点点同学对数据26,36,46,5,52进行统计分析,发现其中一个两位数的个位数字被黑水涂污看不到了,则计算结果与被涂污数字无关的是( )
A.平均数
B.中位数
C.方差
D.标准差
11.测试五位学生的“立定跳远”成绩,得到5个互不相同的数据,在统计时出现一处错误,将最低成绩写得更低了,计算不受影响的是(
)
A.方差
B.标准差
C.平均数
D.中位数
12.某同学对数据28,32,36,42,5,54进行统计分析时,发现其中一个两位数的个位数字被墨水涂污看不清楚了,但计算结果与被涂污的数字无关的是(
)
A.平均数
B.中位数
C.方差
D.标准差
13.已知一组数据的方差是3,则这组数据的标准差是(
)
A.9
B.3
C.
D.
14.某市疾控中心在对10名某传染病确诊病人的流行病史的调查中发现,这10人的潜伏期分别为:5,5,5,7,7,8,8,9,11,14(单位:天),则下列关于这组潜伏期数据的说法中不正确的是( )
A.众数是5天
B.中位数是7.5天
C.平均数是7.9天
D.标准差是2.5天
15.已知数据1,2,3,3,4,5,则下列关于这组数据的说法,错误的是( )
A.平均数是3
B.中位数和众数都是3
C.方差为10
D.标准差是
二、填空题
1.有一组数据如下:2,3,a,5,6,它们的平均数是4,则这组数据的极差是______
2.贝贝在练习“投掷铅球”项目活动中进行了5次测试,测试成绩(单位:分)如下:10,7,9,4,10.则贝贝5次成绩的极差是_____.
3.某班体育委员统计了全班45名同学一周的体育锻炼时间(单位:小时),并绘制了如图的折线统计图,这组数据的中位数是_____,极差是_____,平均数是_____.
4.某次对中学生身高的抽样调查中测得5个同学的身高如下(单位:cm):172,171,175,174,178,则这组数据的方差为________.
5.已知一组数据:x1,x2,x3,…,xn的平均数是2,方差是3,另一组数据:3x1﹣2,3x2﹣2,…3xn﹣2的方差是__________.
6.已知一组数据的方差是,那么另一组数据的方差是______.
7.已知一组数据的方差是则这组数据的标准差是_________.
8.一组数据,1,3,2,5,x的平均数为3,那么这组数据的标准差是______.
9.已知数据x1,x2,x3的平均数为a,方差为b,则数据2x1+3,2x2+3,2x3+3的标准差是_____.
三、解答题
1.已知A组数据如下:
0,1,-2,-1,0,-1,3.
(1)A组数据的中位数是
;
(2)求A组数据的方差;
(3)从A组数据中选取5个数据,记这5个数据为B组数据.
要求B组数据满足两个条件:①
它的平均数与A组数据的平均数相等;②
它的方差比A组数据的方差大.你选取的B组数据是
.
2.6月26日是“国际禁毒日”,某中学组织七、八年级全体学生开展了“禁毒知识”网上竞赛活动.为了解竞赛情况,从两个年级各随机抽取了10名同学的成绩(满分为100分),收集数据为:七年级90,95,95,80,90,80,85,90,85,100;八年级85,85,95,80,95,90,90,90,100,90.
整理数据:
分数
人数
年级
80
85
90
95
100
七年级
2
2
3
2
1
八年级
1
2
4
a
1
分析数据:
平均数
中位数
众数
方差
七年级
89
b
90
39
八年级
c
90
d
30
根据以上信息回答下列问题:
(1)请直接写出表格中a,b,c,d的值;
(2)通过数据分析,你认为哪个年级的成绩比较好?请说明理由;
(3)该校七、八年级共有600人,本次竞赛成绩不低于90分的为“优秀”.估计这两个年级共有多少名学生达到“优秀”?
3.在防疫知识普查考试中,某次测试试题的满分为20分.某校为了解该校部分学生的成绩情况,从该校七、八年级学生中各随机抽取了20名学生的成绩进行了整理、描述和分析,下面给出了部分信息:
抽取的20名七年级学生成绩是:
20,20,20,20,19,19,19,19,18,18,
18,18,18,18,18,17,16,16,15,14.
抽取的40名学生成绩统计表
七年级
八年级
平均分
18
18
众数
a
b
中位数
18
c
方差
2.7
2.7
根据以上信息,解答下列问题:
(1)直接写出上表中a,b,c的值;
(2)在这次测试中,你认为是七年级成绩好,还是八年级成绩好?请说明理由(一条理由即可);
(3)该校七、八年级共有学生1000人,估计此次测试成绩不低于19分的学生有多少人?
4.某校团委举办了一次“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上为合格,达到9分以上(含9分)为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如下.
(1)补充完成下列的成绩统计分析表:(写出方差的计算过程)
(2)甲组6分的人数比乙组6分的人数多_____%.
(3)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是________组学生;(填“甲”或“乙”)
(4)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
5.为了了解学生对“预防新型冠状病毒”知识的掌握情况,学校组织了一次线上知识培训,培训结束后进行测试,试题的满分为分.为了解学生的成绩情况,从七、八年级学生中各随机抽取了名学生的成绩进行了整理、描述和分析,下面给出了部分信息:
抽取的名七年级成绩是:
,,,,,,,,,,
,,,,,,,,,.
抽取的名八年级成绩折线统计图
抽取的名学生成绩统计表
性别
七年级
八年级
平均数
众数
中位数
方差
根据以上信息,解答下列问题:
(1)直接写出上表中,,的值:______,______,_______;
(2)在这次测试中,你认为是七年级成绩好,还是八年级成绩好?请说明理由;
6.某校八年级(1)班甲、乙两男生在5次引体向上测试中有效次数如下:
甲:8,8,7,8,9;乙:5,9,7,10,9;
甲乙两同学引体向上的平均数、众数、中位数、方差如下:
平均数
众数
中位数
方差
甲
8
b
8
0.4
乙
a
9
c
3.2
根据以上信息,回答下列问题:
(1)表格是a= ,b= ,c= .(填数值)
(2)体育老师根据这5次的成绩,决定选择甲同学代表班级参加年级引体向上比赛,选择甲的理由是
.班主任李老师根据去年比赛的成绩(至少9次才能获奖),决定选择乙同学代表班级参加年级引体向上比赛,选择乙的理由是
;
(3)如果乙同学再做一次引体向上,有效次数为8,那么乙同学6次引体向上成绩的平均数
,中位数
,方差
.(填“变大”、“变小”或“不变”)
7.某学校要调查学生关于“新冠肺炎”防治知识的了解情况,从七、八年级各随机抽取了10名学生进行测试(百分制),测试成绩整理、描述和分析如下:
(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100),七年级10名学生的成绩是:96,80,96,86,99,96,90,100,89,82.八年级10名学生的成绩在C组中的数据是:94,90,92.
七、八年级抽取的学生成绩统计表
年级
七年级
八年级
平均数
92
92
中位数
93
b
众数
c
100
方差
52
50.4
根据以上信息,解答下列问题:
(1)直接写出上述图表中a,b,c的值;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握“新冠肺炎”知识较好?请说明理由.
(3)该校七、八年级共1200人参加了此次调查活动,估计参加此次调查活动成绩优秀(x≥90)的学生人数是多少?
答案
一、选择题
1.B.2.C.3.C.4.D.5.A.6.C.7.B.8.B.9.A.
10.B
11.D.12.B
13.D
14.D
15.C.
二、填空题
1.4.
2.6.
3.9,4,9.
4.6.
5.27.
6..
7.2.
8..
9.2.
三、解答题
1.解:(1)把数据按从小到大排列如下:
最中间的数是:
所以这组数据的中位数是:
故答案为:
(2)这组数据的平均数为:
所以这组数据的方差为:
(3)组数据为:.
组数据的平均数为:
组数据的方差为:
由>,
所以组数据符合条件①②.
故答案为:.(答案不唯一)
2.解:(1)观察八年级95分的有2人,故a=2,
七年级的中位数为,故b=90,
八年级的平均数为:×(85+85+95+80+95+90+90+90+100+90)=90,故c=90,
八年级中90分的最多,故d=90;
(2)七、八年级学生成绩的中位数和众数相同,但八年级的平均成绩比七年级高,且从方差看,八年级学生成绩更整齐,综上,八年级的学生成绩好;
(3)∵600×=600×=390(人),
∴该校七、八年级这次竞赛达到优秀的有390人.
3.解:(1)七年级20名学生成绩的众数a=18,八年级成绩的众数b=19,中位数c==18.5;
(2)八年级的成绩好,
∵七年级与八年级成绩的平均分和方差相等,而八年级的中位数大于七年级的中位数,即八年级高分人数稍多,
∴八年级的成绩好;
(3)估计此次测试成绩不低于19分的学生有1000×=450(人).
4.解:(1)甲组:3,6,6,6,6,6,7,8,9,10,中位数为6(分);众数为6(分)
乙组:5,5,6,7,7,8,8,8,8,9,平均数=7.1(分),
S乙2==1.69(分2),众数为8(分);
故答案为:6,6,7.1,1.69,8;
(2)(5-1)÷1=4=400%;
故答案为400;
(3)因为甲组的中位数为6,所以7分在甲组排名属中游略偏上;
所以,小明是甲组学生;
故答案为:甲;
(4)乙组的平均数高于甲组;乙组的中位数高于甲组,所以乙组的成绩要好于甲组.
5.解:(1)七年级成绩的众数为18,
八年级成绩的众数为19,中位数为=18.5,
即a=18,b=19,c=18.5;
故答案为,,;
(2)解:八年级的成绩好
七年级与八年级成绩的平均分和方差相等,而八年级的中位数大于七年级的中位数,即八年级高分人数稍多,
八年级的成绩好.
6.(1),
因为甲中8共出现3次,次数最多,所以b=8
因为乙的有效次数中按顺序排列后处于中间位置的是9,所以中位数c=9;
故答案为a、b、c的值分别是8、8、9;
(2),
∴甲的方差较小,成绩比较稳定,
∴选择甲同学代表班级参加年级引体向上比赛;
∵乙的中位数是9,众数也是9,
∴获奖可能性较大,
∴根据去年比赛的成绩(至少9次才能获奖),决定选择乙同学代表班级参加年级引体向上比赛;
(3)∵原来的平均数是8,增加一次也是8,
∴平均数不变.
∵六次成绩排序为5,7,8,9,9,10,
∴处于中间位置的数为8,9,
∴中位数为
,
∴中位数变小.
后来的方差为,
∴方差变小.
7.解:(1)因为八年级组有人,组有人,组有人,
所以组有人,所以:
即
因为八年级学生成绩的分布:组有人,组有人,组有人,组有人,且成绩是按照从小到大的顺序排列的,所以八年级学生成绩的中位数落在组,而C组中的数据是:94,90,92,
按从小到大排列为:
所以第个,第个数据为:
所以中位数为:分,
因为七年级学生成绩中分有个,出现的次数最多,所以众数分,
故答案为:a=40,b=93,c=96.
(2)八年级掌握得更好.因为七八年级的平均数、中位数相同,
而八年级的众数比七年级高,说明八年级高分的同学更多;
八年级方差比七年级小,说明八年级两极分化差距小.
(3)由题意得:七年级成绩大于或等于分的有人,八年级成绩大于或等于分的有人
(人)
答:参加此次调查活动成绩优秀的学生人数约为780人.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
