北师大版八年级数学上册第三章 位置与坐标单元测试卷(word含答案)
文档属性
| 名称 | 北师大版八年级数学上册第三章 位置与坐标单元测试卷(word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 11:57:58 | ||
图片预览



文档简介
第三单元测试卷
一、选择题(本大题共14个小题,每题2分,共28分)
1.某班级第3组第4排的位置可以用数对(3,4)表示,则数对(1,2)表示的位置是(
)
A.第2组第1排
B.第1组第1排
C.第1组第2排
D.第2组第2排
2.点位于(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.点位于轴左方,距轴3个单位长,位于轴上方,距轴四个单位长,点的坐标是(
)
A.
B.
C.
D.
4.在平面直角坐标系中,点关于y轴的对称点的坐标是(
)
A.
B.
C.
D.
5.如图,小手盖住的点的坐标可能为(
)
A.(5,2)
B.(-6,3)
C.(-4,-6)
D.(3,-4)
6.已知点A的坐标为(1,3-a),若点A到x轴的距离是3
,则a=(
)
A.6
B.0
C.±6
D.0或6
7.若,则点所在的象限是(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8.已知点在第二象限,到
轴的距离是,到轴的距离是,点的坐标为(
)
A.
B.
C.
D.
9.如果点在第四象限,则的取值范围是(
)
A.
B.
C.
D.
10.已知点P(a+l,2a-3)关于x轴的对称点在第一象限,则a的取值范围是(
)
A.
B.
C.
D.
11.已知点M
(3,﹣2),N(﹣3,﹣2),则直线MN与x轴、y轴的位置关系分别为( )
A.平行,垂直
B.平行,平行
C.垂直,平行
D.相交,相交
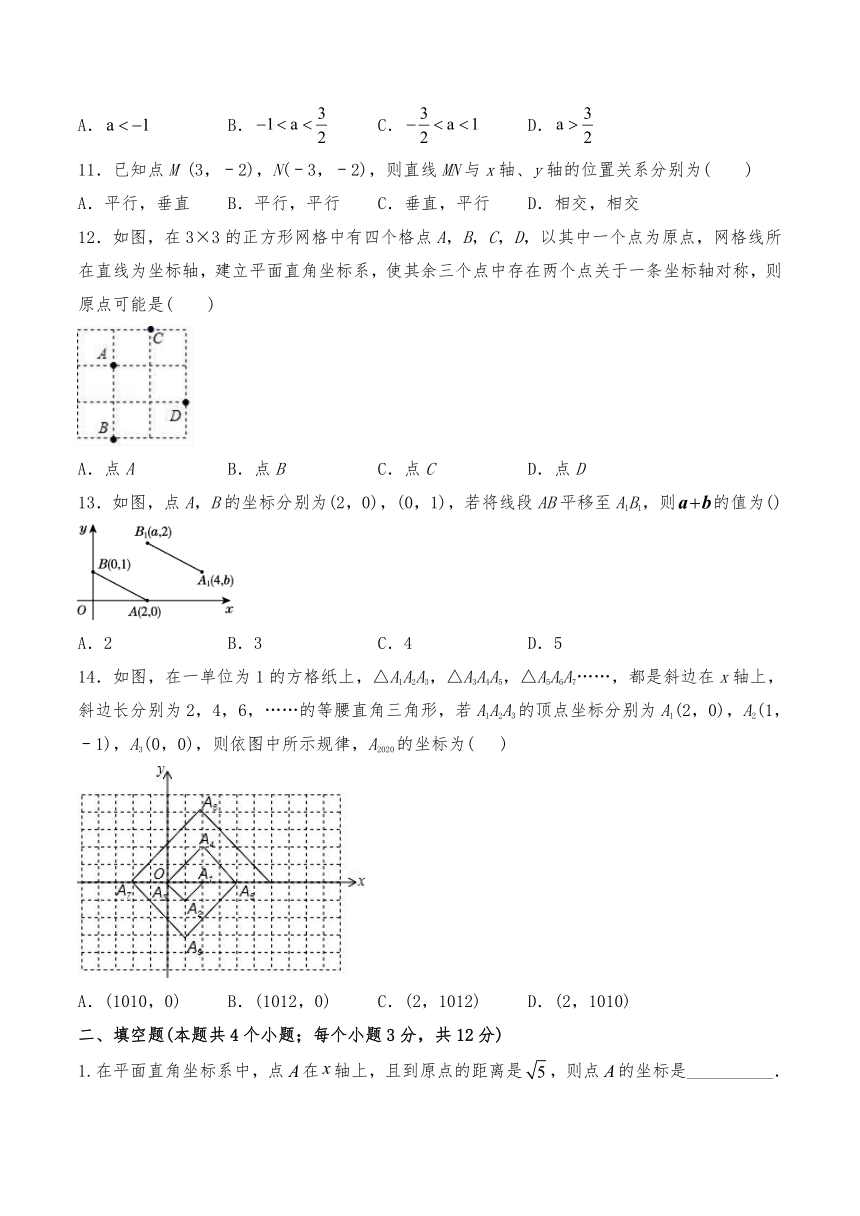
12.如图,在3×3的正方形网格中有四个格点A,B,C,D,以其中一个点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点可能是( )
A.点A
B.点B
C.点C
D.点D
13.如图,点A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则的值为()
A.2
B.3
C.4
D.5
14.如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7……,都是斜边在x轴上,斜边长分别为2,4,6,……的等腰直角三角形,若A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2020的坐标为(
)
A.(1010,0)
B.(1012,0)
C.(2,1012)
D.(2,1010)
二、填空题(本题共4个小题;每个小题3分,共12分)
1.在平面直角坐标系中,点在轴上,且到原点的距离是,则点的坐标是__________.
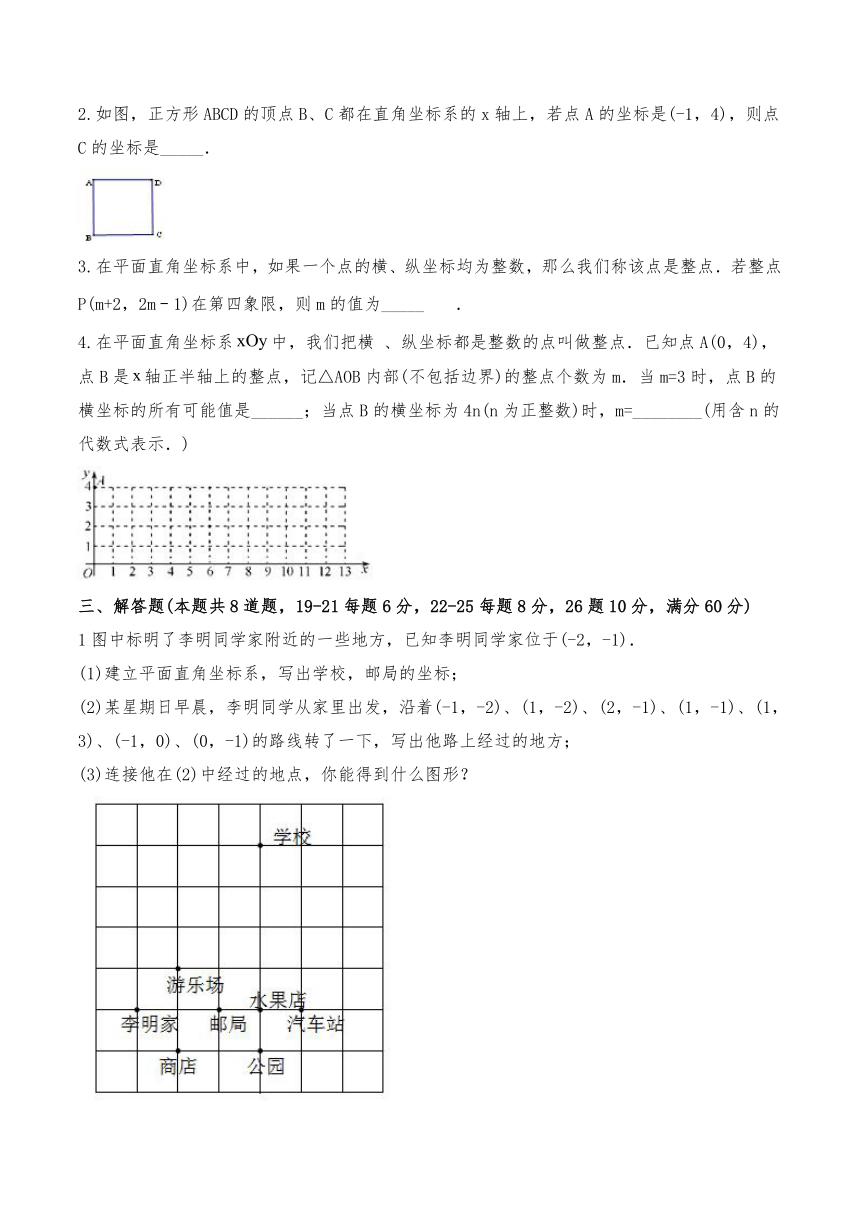
2.如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,若点A的坐标是(-1,4),则点C的坐标是_____.
3.在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是整点.若整点P(m+2,2m﹣1)在第四象限,则m的值为_____.
4.在平面直角坐标系中,我们把横
、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是______;当点B的横坐标为4n(n为正整数)时,m=________(用含n的代数式表示.)
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
1图中标明了李明同学家附近的一些地方,已知李明同学家位于(-2,-1).
(1)建立平面直角坐标系,写出学校,邮局的坐标;
(2)某星期日早晨,李明同学从家里出发,沿着(-1,-2)、(1,-2)、(2,-1)、(1,-1)、(1,3)、(-1,0)、(0,-1)的路线转了一下,写出他路上经过的地方;
(3)连接他在(2)中经过的地点,你能得到什么图形?
2.在平面直角坐标系中,点在第四象限.
(1)求的取值范围;
(2)若点到轴的距离为,求点到轴的距离.
3.如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式|a-2|+(b-3)2=0,(c-4)2≤0.
(1)求a,b,c的值;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
4.在平面直角坐标系中,为坐标原点.
(1)已知点在轴上,求点的坐标.
(2)已知两点,若轴,点在第一象限,求的值,并确定的取值范围.
(3)在(1)(2)的条件下,如果线段的长度是5,求以为顶点的三角形的面积.
5.对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),
则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为
;
(Ⅱ)若点P的“5属派生点”P′的坐标为(3,﹣9),求点P的坐标;
(Ⅲ)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
6.如图,一只乌鸦从其巢(点O)飞出,飞向其巢东6km北10km的一点A,在该点它发现有一个稻草人,所以就转向,再向东8km北4km的地方B飞去.在那里它吃了一些谷物后立即返巢O,假设乌鸦总是沿直线飞行的,则乌鸦所飞的路径构成了一个三角形OAB
(1)若点O的坐标为(0,0),点A的坐标为(6,10),写出点B的坐标.
(2)试求三角形OAB的面积.
7.平面直角坐标系中,已知点A的坐标为(m-1,3),点B的坐标为(﹣4,2m-5),若直线AB//x轴,点P为线段AB上任意一点(不与A、B重合),点Q是点P关于y轴的对称点.
(1)求点A和点B的坐标;
(2)求△ABO的面积;
(3)如果△OPA的面积是△OPQ的面积的2倍,求点P的坐标.
8.如图①,长方形OABC,.点P从点A出发,以每秒1个单位长度的速度沿边向终点C运动,设点P运动时间为.
(1)B点坐标为
;
(2)①当t=2时,则BP=
;当t=4时,BP=
;
②当时,CP=
;(用含t的式子表示)
(3)如图②,点p出发3s后,一直线l从y轴位置出发沿x轴正方向运动,且始终与y轴平行,运动速度为每秒2个单位长度.当t为何值时,点到直线的距离为2?
答案
一、选择题
1.C.
2.D.3.B.4.B.5.C.6.D.7.D.8.B
9.D.10.B.11.A.12.D.13.B.14.D.
二、填空题
1.或.
2.(3,0)
3.﹣1或0.
4.3或4
6n-3
三、解答题
1.(1)根据题意建立的平面直角坐标系如图所示,
学校(1,3),邮局(0,-1);
(2)他经过:商店,公园,汽车站,水果店,学校,游乐场,邮局;
(3)得到的图形像一艘帆船.
2.解:(1)由题知
解得;
(2)∵点P在第四象限,点到轴的距离为
∴,
解得
得,
所以点到轴的距离为.
3.解:(1)由已知,
及
可得:,,;
(2),
,
(3)因为,
,
则,
所以存在点使.
4.(1)∵点P(a-1,3a+6)在y轴上,
∴a-1=0,
解得:a=1,
∴3a+6=9,
∴点P坐标为(0,9).
(2)∵AB//x轴,A(-3,m),B(n,4),
∴m=4,
∵点B在第一象限,
∴n>0.
(3)∵AB=5,A(-3,4)
∴|-3-n|=5,
解得:n=2或n=-8,
∵n>0,
∴n=2,
∴以P、O、B为顶点的三角形的面积为=×OP×n=×9×2=9.
5.(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为(﹣2+3×3,﹣2×3+3),即(7,﹣3),
故答案为:(7,﹣3);
(Ⅱ)设P(x,y),
依题意,得方程组:,
解得,
∴点P(﹣2,1).
(Ⅲ)∵点P(a,b)在x轴的正半轴上,
∴b=0,a>0.
∴点P的坐标为(a,0),点P′的坐标为(a,ka),
∴线段PP′的长为点P′到x轴距离为|ka|,
∵P在x轴正半轴,线段OP的长为a,
根据题意,有|PP'|=2|OP|,
∴|ka|=2a,
∵a>0,
∴|k|=2.
从而k=±2.
6.(1)点O的坐标为,点A的坐标为
点B的横坐标为,纵坐标为
故点B的坐标为;
(2)由点B的坐标可知,点B位于原点O北偏东的位置
如图,点C的坐标为,其也位于原点O北偏东的位置
则点共线
点C与点A的纵坐标相等
AC与水平方向平行
又
,点O到AC的距离为,点B到AC的距离为
则
故三角形OAB的面积为.
7.解:(1)∵AB//x轴
∴A、B两点的纵坐标相同,即3=2m-5
解得:m=4;
即点A的坐标为(3,3),点B的坐标为(-4,3);
(2)△ABO的面积为:AB?OC=×7×3=.
(3)设点P的坐标为(m,3),则点Q的坐标为(-m,3)
即,
∴AP=2PQ;
①当点P在y轴左侧时,3-m=-2m×2,
解得:m=1
,
∴点P坐标为(﹣1,3);
②当点P在y轴右侧时,则3﹣m=2m×2,
解得:m=.
∴点P坐标为(,3)
故P(﹣1,3)或(,3).
8.(1)∵,
∴,
∴
(2)①当时,
∴
当时,
∴
②当时,
∴
(3)分两种情况:
当点与直线相遇前时
∴
当点与直线相遇后
∴
∴当或时点到直线的距离为.
一、选择题(本大题共14个小题,每题2分,共28分)
1.某班级第3组第4排的位置可以用数对(3,4)表示,则数对(1,2)表示的位置是(
)
A.第2组第1排
B.第1组第1排
C.第1组第2排
D.第2组第2排
2.点位于(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.点位于轴左方,距轴3个单位长,位于轴上方,距轴四个单位长,点的坐标是(
)
A.
B.
C.
D.
4.在平面直角坐标系中,点关于y轴的对称点的坐标是(
)
A.
B.
C.
D.
5.如图,小手盖住的点的坐标可能为(
)
A.(5,2)
B.(-6,3)
C.(-4,-6)
D.(3,-4)
6.已知点A的坐标为(1,3-a),若点A到x轴的距离是3
,则a=(
)
A.6
B.0
C.±6
D.0或6
7.若,则点所在的象限是(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8.已知点在第二象限,到
轴的距离是,到轴的距离是,点的坐标为(
)
A.
B.
C.
D.
9.如果点在第四象限,则的取值范围是(
)
A.
B.
C.
D.
10.已知点P(a+l,2a-3)关于x轴的对称点在第一象限,则a的取值范围是(
)
A.
B.
C.
D.
11.已知点M
(3,﹣2),N(﹣3,﹣2),则直线MN与x轴、y轴的位置关系分别为( )
A.平行,垂直
B.平行,平行
C.垂直,平行
D.相交,相交
12.如图,在3×3的正方形网格中有四个格点A,B,C,D,以其中一个点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点可能是( )
A.点A
B.点B
C.点C
D.点D
13.如图,点A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则的值为()
A.2
B.3
C.4
D.5
14.如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7……,都是斜边在x轴上,斜边长分别为2,4,6,……的等腰直角三角形,若A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2020的坐标为(
)
A.(1010,0)
B.(1012,0)
C.(2,1012)
D.(2,1010)
二、填空题(本题共4个小题;每个小题3分,共12分)
1.在平面直角坐标系中,点在轴上,且到原点的距离是,则点的坐标是__________.
2.如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,若点A的坐标是(-1,4),则点C的坐标是_____.
3.在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是整点.若整点P(m+2,2m﹣1)在第四象限,则m的值为_____.
4.在平面直角坐标系中,我们把横
、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是______;当点B的横坐标为4n(n为正整数)时,m=________(用含n的代数式表示.)
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
1图中标明了李明同学家附近的一些地方,已知李明同学家位于(-2,-1).
(1)建立平面直角坐标系,写出学校,邮局的坐标;
(2)某星期日早晨,李明同学从家里出发,沿着(-1,-2)、(1,-2)、(2,-1)、(1,-1)、(1,3)、(-1,0)、(0,-1)的路线转了一下,写出他路上经过的地方;
(3)连接他在(2)中经过的地点,你能得到什么图形?
2.在平面直角坐标系中,点在第四象限.
(1)求的取值范围;
(2)若点到轴的距离为,求点到轴的距离.
3.如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式|a-2|+(b-3)2=0,(c-4)2≤0.
(1)求a,b,c的值;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
4.在平面直角坐标系中,为坐标原点.
(1)已知点在轴上,求点的坐标.
(2)已知两点,若轴,点在第一象限,求的值,并确定的取值范围.
(3)在(1)(2)的条件下,如果线段的长度是5,求以为顶点的三角形的面积.
5.对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),
则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为
;
(Ⅱ)若点P的“5属派生点”P′的坐标为(3,﹣9),求点P的坐标;
(Ⅲ)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
6.如图,一只乌鸦从其巢(点O)飞出,飞向其巢东6km北10km的一点A,在该点它发现有一个稻草人,所以就转向,再向东8km北4km的地方B飞去.在那里它吃了一些谷物后立即返巢O,假设乌鸦总是沿直线飞行的,则乌鸦所飞的路径构成了一个三角形OAB
(1)若点O的坐标为(0,0),点A的坐标为(6,10),写出点B的坐标.
(2)试求三角形OAB的面积.
7.平面直角坐标系中,已知点A的坐标为(m-1,3),点B的坐标为(﹣4,2m-5),若直线AB//x轴,点P为线段AB上任意一点(不与A、B重合),点Q是点P关于y轴的对称点.
(1)求点A和点B的坐标;
(2)求△ABO的面积;
(3)如果△OPA的面积是△OPQ的面积的2倍,求点P的坐标.
8.如图①,长方形OABC,.点P从点A出发,以每秒1个单位长度的速度沿边向终点C运动,设点P运动时间为.
(1)B点坐标为
;
(2)①当t=2时,则BP=
;当t=4时,BP=
;
②当时,CP=
;(用含t的式子表示)
(3)如图②,点p出发3s后,一直线l从y轴位置出发沿x轴正方向运动,且始终与y轴平行,运动速度为每秒2个单位长度.当t为何值时,点到直线的距离为2?
答案
一、选择题
1.C.
2.D.3.B.4.B.5.C.6.D.7.D.8.B
9.D.10.B.11.A.12.D.13.B.14.D.
二、填空题
1.或.
2.(3,0)
3.﹣1或0.
4.3或4
6n-3
三、解答题
1.(1)根据题意建立的平面直角坐标系如图所示,
学校(1,3),邮局(0,-1);
(2)他经过:商店,公园,汽车站,水果店,学校,游乐场,邮局;
(3)得到的图形像一艘帆船.
2.解:(1)由题知
解得;
(2)∵点P在第四象限,点到轴的距离为
∴,
解得
得,
所以点到轴的距离为.
3.解:(1)由已知,
及
可得:,,;
(2),
,
(3)因为,
,
则,
所以存在点使.
4.(1)∵点P(a-1,3a+6)在y轴上,
∴a-1=0,
解得:a=1,
∴3a+6=9,
∴点P坐标为(0,9).
(2)∵AB//x轴,A(-3,m),B(n,4),
∴m=4,
∵点B在第一象限,
∴n>0.
(3)∵AB=5,A(-3,4)
∴|-3-n|=5,
解得:n=2或n=-8,
∵n>0,
∴n=2,
∴以P、O、B为顶点的三角形的面积为=×OP×n=×9×2=9.
5.(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为(﹣2+3×3,﹣2×3+3),即(7,﹣3),
故答案为:(7,﹣3);
(Ⅱ)设P(x,y),
依题意,得方程组:,
解得,
∴点P(﹣2,1).
(Ⅲ)∵点P(a,b)在x轴的正半轴上,
∴b=0,a>0.
∴点P的坐标为(a,0),点P′的坐标为(a,ka),
∴线段PP′的长为点P′到x轴距离为|ka|,
∵P在x轴正半轴,线段OP的长为a,
根据题意,有|PP'|=2|OP|,
∴|ka|=2a,
∵a>0,
∴|k|=2.
从而k=±2.
6.(1)点O的坐标为,点A的坐标为
点B的横坐标为,纵坐标为
故点B的坐标为;
(2)由点B的坐标可知,点B位于原点O北偏东的位置
如图,点C的坐标为,其也位于原点O北偏东的位置
则点共线
点C与点A的纵坐标相等
AC与水平方向平行
又
,点O到AC的距离为,点B到AC的距离为
则
故三角形OAB的面积为.
7.解:(1)∵AB//x轴
∴A、B两点的纵坐标相同,即3=2m-5
解得:m=4;
即点A的坐标为(3,3),点B的坐标为(-4,3);
(2)△ABO的面积为:AB?OC=×7×3=.
(3)设点P的坐标为(m,3),则点Q的坐标为(-m,3)
即,
∴AP=2PQ;
①当点P在y轴左侧时,3-m=-2m×2,
解得:m=1
,
∴点P坐标为(﹣1,3);
②当点P在y轴右侧时,则3﹣m=2m×2,
解得:m=.
∴点P坐标为(,3)
故P(﹣1,3)或(,3).
8.(1)∵,
∴,
∴
(2)①当时,
∴
当时,
∴
②当时,
∴
(3)分两种情况:
当点与直线相遇前时
∴
当点与直线相遇后
∴
∴当或时点到直线的距离为.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
