第三章 勾股定理专项训练 勾股定理及直角三角形的判别条件同步练习题 (含答案)
文档属性
| 名称 | 第三章 勾股定理专项训练 勾股定理及直角三角形的判别条件同步练习题 (含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 21:21:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专项训练
勾股定理及直角三角形的判别条件
类型一 判断三角形的形状
1.已知a,b,c是△ABC的三边长,且满足关系式(c2-a2-b2)2+|a-b|=0,则△ABC的形状为___________.
类型二 说明线段垂直
2.甲、乙两艘客轮同时离开港口,航行的速度都是400 m/min,甲客轮用15 min到达A处,乙客轮用20 min到达B处.若A、B两处的直线距离为10000 m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
A.北偏西30°方向 B.南偏西30°方向
C.南偏东60°方向 D.南偏东30°方向
类型三 求线段的长
3.如图所示,在Rt△ABC中,∠ACB=90°,AE为△ABC的角平分线,且ED⊥AB,若AC=6,BC=8,则BD的长为( )
A.2 B.3 C.4 D.5
4.如图所示,长方体盒子的长、宽、高分别是9 cm、9 cm、24 cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,它至少要爬行__________ cm.
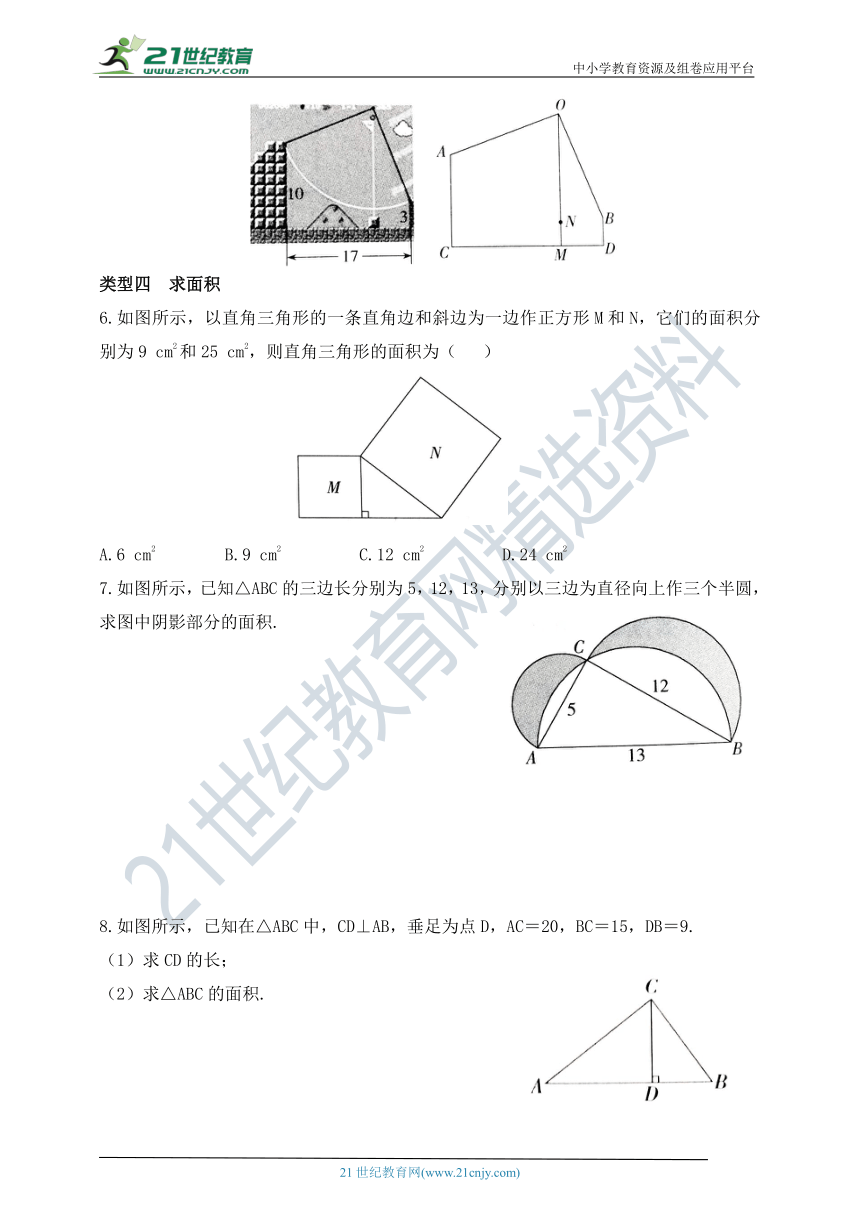
5.如图所示,在一款名为超级玛丽的游戏中,马里奥到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,马里奥在荡绳索过程中离地面的最低点的高度MN=( )
类型四 求面积
6.如图所示,以直角三角形的一条直角边和斜边为一边作正方形M和N,它们的面积分别为9 cm2和25 cm2,则直角三角形的面积为( )
A.6 cm2 B.9 cm2 C.12 cm2 D.24 cm2
7.如图所示,已知△ABC的三边长分别为5,12,13,分别以三边为直径向上作三个半圆,求图中阴影部分的面积.
8.如图所示,已知在△ABC中,CD⊥AB,垂足为点D,AC=20,BC=15,DB=9.
(1)求CD的长;
(2)求△ABC的面积.
类型五 在探究动点的存在性问题中的应用
9.如图所示,在Rt△ABC中,∠ACB=90°,AB=20 cm,AC=16 cm,点P从点A出发,以每秒1 cm的速度向点C运动,连接PB,设运动时间为t秒(t>0).
(1)BC=__________ cm;
(2)当PA=PB时,求t的值.
参考答案
1. 等腰直角三角形
2.C 3.C
4. 30 5. 2米
6.A
7.解析 ∵52+122=169=132,∴△ABC是直角三角形,
由题图可知,阴影部分的面积
=.
8.解析 (1)∵CD⊥AB,∴∠CDB=∠CDA=90°,
在Rt△BDC中,CD2+BD2=BC2,CD2+92=152,∴CD=12.
(2)在Rt△ADC中,AD2+CD2=AC2,
∴AD2+122=202,∴AD=16,∴AB=AD+BD=16+9=25.
∴S△ABC=AB·CD=×25×12=150.
9.解析 (1)∵在Rt△ABC中,∠ACB=9°,AB=20cm,AC=16cm,
∴BC2=AB2-AC2=202-162=144,∴BC=12cm.
故答案为12.
(2)在Rt△PCB中,∠PCB=90°,PC=(16-t)cm,PB=PA=tcm,
由勾股定理,得PC2+BC2=PB2,即(16-t)2+122=t2,解得t=12.5,
∴当PA=PB时,t的值为12.5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专项训练
勾股定理及直角三角形的判别条件
类型一 判断三角形的形状
1.已知a,b,c是△ABC的三边长,且满足关系式(c2-a2-b2)2+|a-b|=0,则△ABC的形状为___________.
类型二 说明线段垂直
2.甲、乙两艘客轮同时离开港口,航行的速度都是400 m/min,甲客轮用15 min到达A处,乙客轮用20 min到达B处.若A、B两处的直线距离为10000 m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
A.北偏西30°方向 B.南偏西30°方向
C.南偏东60°方向 D.南偏东30°方向
类型三 求线段的长
3.如图所示,在Rt△ABC中,∠ACB=90°,AE为△ABC的角平分线,且ED⊥AB,若AC=6,BC=8,则BD的长为( )
A.2 B.3 C.4 D.5
4.如图所示,长方体盒子的长、宽、高分别是9 cm、9 cm、24 cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,它至少要爬行__________ cm.
5.如图所示,在一款名为超级玛丽的游戏中,马里奥到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,马里奥在荡绳索过程中离地面的最低点的高度MN=( )
类型四 求面积
6.如图所示,以直角三角形的一条直角边和斜边为一边作正方形M和N,它们的面积分别为9 cm2和25 cm2,则直角三角形的面积为( )
A.6 cm2 B.9 cm2 C.12 cm2 D.24 cm2
7.如图所示,已知△ABC的三边长分别为5,12,13,分别以三边为直径向上作三个半圆,求图中阴影部分的面积.
8.如图所示,已知在△ABC中,CD⊥AB,垂足为点D,AC=20,BC=15,DB=9.
(1)求CD的长;
(2)求△ABC的面积.
类型五 在探究动点的存在性问题中的应用
9.如图所示,在Rt△ABC中,∠ACB=90°,AB=20 cm,AC=16 cm,点P从点A出发,以每秒1 cm的速度向点C运动,连接PB,设运动时间为t秒(t>0).
(1)BC=__________ cm;
(2)当PA=PB时,求t的值.
参考答案
1. 等腰直角三角形
2.C 3.C
4. 30 5. 2米
6.A
7.解析 ∵52+122=169=132,∴△ABC是直角三角形,
由题图可知,阴影部分的面积
=.
8.解析 (1)∵CD⊥AB,∴∠CDB=∠CDA=90°,
在Rt△BDC中,CD2+BD2=BC2,CD2+92=152,∴CD=12.
(2)在Rt△ADC中,AD2+CD2=AC2,
∴AD2+122=202,∴AD=16,∴AB=AD+BD=16+9=25.
∴S△ABC=AB·CD=×25×12=150.
9.解析 (1)∵在Rt△ABC中,∠ACB=9°,AB=20cm,AC=16cm,
∴BC2=AB2-AC2=202-162=144,∴BC=12cm.
故答案为12.
(2)在Rt△PCB中,∠PCB=90°,PC=(16-t)cm,PB=PA=tcm,
由勾股定理,得PC2+BC2=PB2,即(16-t)2+122=t2,解得t=12.5,
∴当PA=PB时,t的值为12.5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
