黑龙江省齐齐哈尔市昂昂溪区2020-2021学年八年级上学期期末考试数学试题(word版含答案)
文档属性
| 名称 | 黑龙江省齐齐哈尔市昂昂溪区2020-2021学年八年级上学期期末考试数学试题(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 234.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 00:00:00 | ||
图片预览


文档简介
学校
班级
姓名
考号
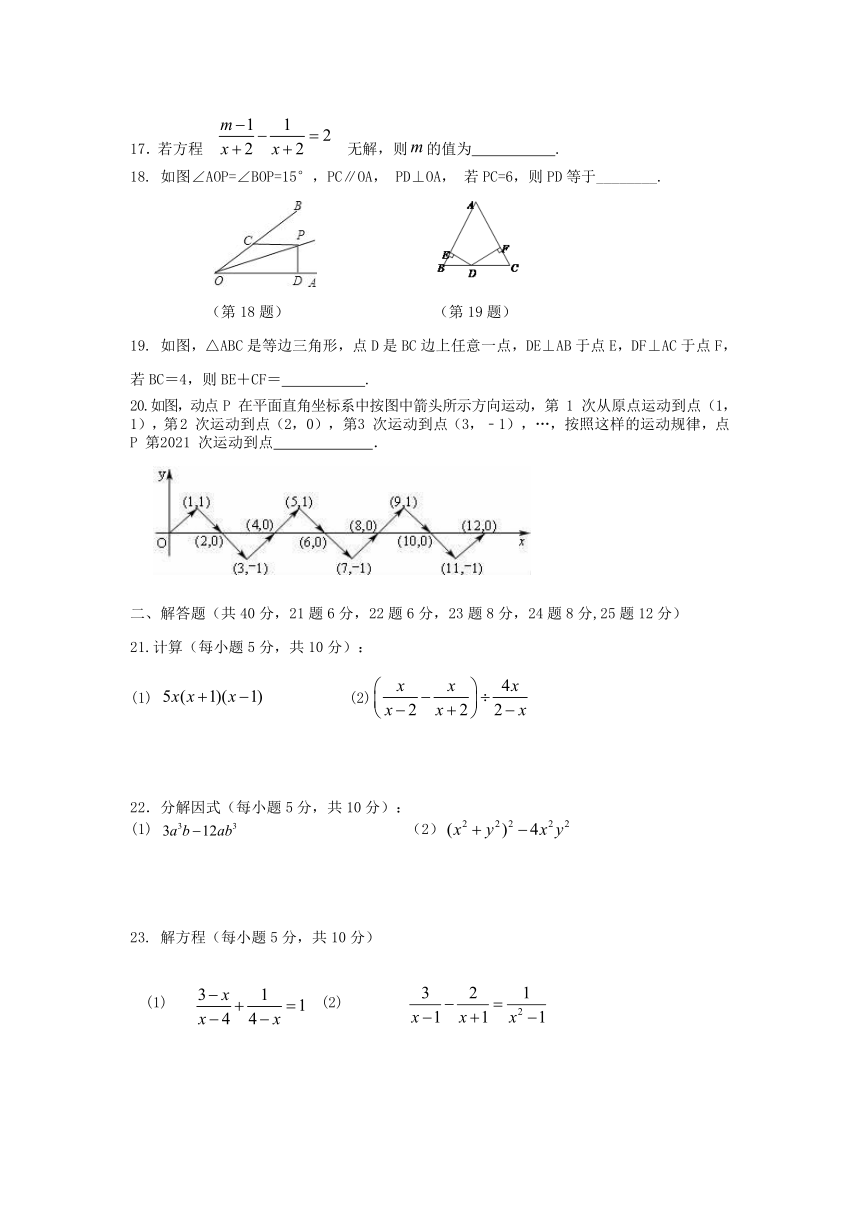
2020--2021学年度上学期期末质量测查
八年级数学试卷
题号
一
二
三
总分
21
22
23
24
25
26
得分
考生须知:1、本卷三个大题,满分120分,答题时间90分钟.
请在答题卡上作答.
选择题(每小题3分,共计30分)
1.
下列四个图形中,是轴对称图形的有(
)
A.
4个
B.
3个
C.
2个
D.
1个
2.
下列计算中不正确的是(
)
A.
a2?a4=a6
B.
a6÷a3=a3
C.
(ab)3=a3b3
D.
(m3n-3m2n+
m2)
÷m2
=mn-3n
3.
在△ABC和△A′B′C′中,AB=
A′B′,∠B=∠B′,补充条件后仍不一定保证△ABC≌△A′B′C′,则补充的这个条件是(
)
A
BC=
B′C′
B.
AC=
A′C′
C.
∠A=∠A′
D.
∠C=∠C′
4.
已知有理数x,y满足+=0,则以x,y的值为两边长的等腰三角形的周长是(
)
A.
20或16
B.
20
C.
16
D.
以上都不对
5.一个多边形的内角和是外角和的倍,则这个多边形的边数为(
)
A.
B.
C.
D.
6.如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处,已知BC=24,∠B=30°,则DE的长是(
)
A.12
B.10
C.8
D.6
7.
如图,在△ABC中,PM、QN分别是AB、AC的垂直平分线,∠BAC=100°那么∠PAQ等于(
)
A.
50°
B.
40°
C.
30°
D.
20°
8.若
,则
的值为(
)
A.5
B.0
C.3或-7
D.4或5
(第7题)
(第9题)
(第10题)
9.
如图,正方形ABCD的面积为,是等边三角形,点E在正方形ABCD内,在对角线AC上有一点,使PD+PE的和最小,则这个最小值为(
).
A.
B.
C.
D.
10.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个结论,你发现的结论是(
)
A.2∠A=∠1-∠2
B.3∠A=2(∠1-∠2)
C.3∠A=2∠1-∠2
D.∠A=∠1-∠2
二、填空题(每小题3分,共计30分)
11.研究表明,H1N1流感球形病毒细胞的直径约为0.00000156m,用科学记数法表示这个数为
m.
12.若分式,则__________.
13.计算3a
2b3
?(-2ab)-2
=
.
中,,,AD是的中线,设AD长为m,则m的取值范围是_______________.
15.
若是完全平方式,则k=_____________.
16.如图所示,已知BO平分,CO平分,过O点的直线若,,则的周长为?
?
?
?
?.
17.若方程无解,则的值为
.
18.
如图∠AOP=∠BOP=15°,PC∥OA,
PD⊥OA,
若PC=6,则PD等于________.
(第18题)
(第19题)
19.
如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,若BC=4,则BE+CF=
.
20.如图,动点
P
在平面直角坐标系中按图中箭头所示方向运动,第
1
次从原点运动到点(1,1),第
2
次运动到点(2,0),第
3
次运动到点(3,﹣1),…,按照这样的运动规律,点
P
第
2021
次运动到点
.
解答题(共40分,21题6分,22题6分,23题8分,24题8分,25题12分)
21.计算(每小题5分,共10分):
(2)
22.分解因式(每小题5分,共10分):
(1)
(2)
解方程(每小题5分,共10分)
(1)
(2)
24.(10分)
如图:在△ABC中∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作CF⊥AE,
垂足为F,过B作BD⊥BC交CF的延长线于D.
求证:(1)AE=CD.(2)若AC=12cm,求BD的长.
25.(8分)某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球回校后,王老师和李老师编写了一道题:
同学们,请求出篮球和排球的单价各是多少元?
27.(12分)
如图,在平面直角坐标系中,点A的坐标为(2,0),以OA为边在第四象限做等边△AOB,点C为x轴正半轴一动点(OC
>
2),连接BC,以BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
(1)试问△OBC与△ABD全等吗?并证明你的结论;
(2)随着点C位置的变化,∠AEO是否会发生变化?若没有变化,求出∠AEO的度数;若有变化,请说明理由.
(3)若在x轴上有一动点P,使△PAE是等腰三角形,请直接写出满足条件的P点坐标.
2020--2021学年度上学期期末质量测查
八年级数学试卷参考答案
选择题(每题3分,共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
D
B
B
A
C
D
C
C
A
二、填空题(每题3分,共30分)
11.
1.56×10-6
12.
4
13.
14.
15.±2
16.
26
17.
2
18.
3
19.
2
20.
(2021,1)
三、解答题(共60分,21题10分,22题10分,23题10分,24题10分,25题8分,26题12分)
21.(每小题5分,共10分)(1)5x3-5x
(2)
22.(每小题5分,共10分)(1)
3ab(a+2b)(a-2b)
(2)
(x+y)2(x-y)2
23.(每小题5分,共10分)(1)x=3
(2)x=-4.
24.证明:(1)证明:∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°.-------------1分
∴∠D=∠AEC.-------------------------------3分
又∵∠DBC=∠ECA=90°,且BC=CA,
在△DBC和△ECA中,
∴△DBC≌△ECA(AAS).--------------------------5分
∴AE=CD;--------------------------------------6分
(2)
由(1)可得△DBC≌△ECA
∴CE=BD,---------------------------------7分
∵BC=AC=12cm
AE是BC的中线,
∴,------------------------9分
∴BD=CE=16cm.---------------------------------10分
25.解:设排球的单价为x元,则篮球的单价为元,根据题意,得
-------------------------------------------3分
解得.-------------------5分
经检验,是原方程的解,且符合题意.------6分
∴.
答:排球的单价为50元,篮球的单价为80元.--------8分
解:(1)△OBC≌△ABD.-----------------------------1分
理由:∵△AOB和△CBD是等边三角形,
∴OB=AB,∠OBA=∠OAB=60°,
BC=BD,∠CBD=60°,-------------------------------2
∴∠OBA+∠ABC=∠CBD+∠ABC,即∠OBC=∠ABD-----------3分
在△OBC和△ABD中,
∴△OBC≌△ABD(SAS).-------------------------------4分
(2)∵△OBC≌△ABD,
∴∠BAD=∠BOC=60°,----------------------------------5分
又∵∠OAB=60°,
∴∠OAE=180°﹣∠OAB﹣∠BAD=60°----------------------6分
∴∠AEO=30°------------------------------------------7分
∴随着点C位置的变化,∠AEO不会发生变化----------------8分
(3)(-2,0)或(6,0).-------------------------------------12分
班级
姓名
考号
2020--2021学年度上学期期末质量测查
八年级数学试卷
题号
一
二
三
总分
21
22
23
24
25
26
得分
考生须知:1、本卷三个大题,满分120分,答题时间90分钟.
请在答题卡上作答.
选择题(每小题3分,共计30分)
1.
下列四个图形中,是轴对称图形的有(
)
A.
4个
B.
3个
C.
2个
D.
1个
2.
下列计算中不正确的是(
)
A.
a2?a4=a6
B.
a6÷a3=a3
C.
(ab)3=a3b3
D.
(m3n-3m2n+
m2)
÷m2
=mn-3n
3.
在△ABC和△A′B′C′中,AB=
A′B′,∠B=∠B′,补充条件后仍不一定保证△ABC≌△A′B′C′,则补充的这个条件是(
)
A
BC=
B′C′
B.
AC=
A′C′
C.
∠A=∠A′
D.
∠C=∠C′
4.
已知有理数x,y满足+=0,则以x,y的值为两边长的等腰三角形的周长是(
)
A.
20或16
B.
20
C.
16
D.
以上都不对
5.一个多边形的内角和是外角和的倍,则这个多边形的边数为(
)
A.
B.
C.
D.
6.如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处,已知BC=24,∠B=30°,则DE的长是(
)
A.12
B.10
C.8
D.6
7.
如图,在△ABC中,PM、QN分别是AB、AC的垂直平分线,∠BAC=100°那么∠PAQ等于(
)
A.
50°
B.
40°
C.
30°
D.
20°
8.若
,则
的值为(
)
A.5
B.0
C.3或-7
D.4或5
(第7题)
(第9题)
(第10题)
9.
如图,正方形ABCD的面积为,是等边三角形,点E在正方形ABCD内,在对角线AC上有一点,使PD+PE的和最小,则这个最小值为(
).
A.
B.
C.
D.
10.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个结论,你发现的结论是(
)
A.2∠A=∠1-∠2
B.3∠A=2(∠1-∠2)
C.3∠A=2∠1-∠2
D.∠A=∠1-∠2
二、填空题(每小题3分,共计30分)
11.研究表明,H1N1流感球形病毒细胞的直径约为0.00000156m,用科学记数法表示这个数为
m.
12.若分式,则__________.
13.计算3a
2b3
?(-2ab)-2
=
.
中,,,AD是的中线,设AD长为m,则m的取值范围是_______________.
15.
若是完全平方式,则k=_____________.
16.如图所示,已知BO平分,CO平分,过O点的直线若,,则的周长为?
?
?
?
?.
17.若方程无解,则的值为
.
18.
如图∠AOP=∠BOP=15°,PC∥OA,
PD⊥OA,
若PC=6,则PD等于________.
(第18题)
(第19题)
19.
如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,若BC=4,则BE+CF=
.
20.如图,动点
P
在平面直角坐标系中按图中箭头所示方向运动,第
1
次从原点运动到点(1,1),第
2
次运动到点(2,0),第
3
次运动到点(3,﹣1),…,按照这样的运动规律,点
P
第
2021
次运动到点
.
解答题(共40分,21题6分,22题6分,23题8分,24题8分,25题12分)
21.计算(每小题5分,共10分):
(2)
22.分解因式(每小题5分,共10分):
(1)
(2)
解方程(每小题5分,共10分)
(1)
(2)
24.(10分)
如图:在△ABC中∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作CF⊥AE,
垂足为F,过B作BD⊥BC交CF的延长线于D.
求证:(1)AE=CD.(2)若AC=12cm,求BD的长.
25.(8分)某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球回校后,王老师和李老师编写了一道题:
同学们,请求出篮球和排球的单价各是多少元?
27.(12分)
如图,在平面直角坐标系中,点A的坐标为(2,0),以OA为边在第四象限做等边△AOB,点C为x轴正半轴一动点(OC
>
2),连接BC,以BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
(1)试问△OBC与△ABD全等吗?并证明你的结论;
(2)随着点C位置的变化,∠AEO是否会发生变化?若没有变化,求出∠AEO的度数;若有变化,请说明理由.
(3)若在x轴上有一动点P,使△PAE是等腰三角形,请直接写出满足条件的P点坐标.
2020--2021学年度上学期期末质量测查
八年级数学试卷参考答案
选择题(每题3分,共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
D
B
B
A
C
D
C
C
A
二、填空题(每题3分,共30分)
11.
1.56×10-6
12.
4
13.
14.
15.±2
16.
26
17.
2
18.
3
19.
2
20.
(2021,1)
三、解答题(共60分,21题10分,22题10分,23题10分,24题10分,25题8分,26题12分)
21.(每小题5分,共10分)(1)5x3-5x
(2)
22.(每小题5分,共10分)(1)
3ab(a+2b)(a-2b)
(2)
(x+y)2(x-y)2
23.(每小题5分,共10分)(1)x=3
(2)x=-4.
24.证明:(1)证明:∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°.-------------1分
∴∠D=∠AEC.-------------------------------3分
又∵∠DBC=∠ECA=90°,且BC=CA,
在△DBC和△ECA中,
∴△DBC≌△ECA(AAS).--------------------------5分
∴AE=CD;--------------------------------------6分
(2)
由(1)可得△DBC≌△ECA
∴CE=BD,---------------------------------7分
∵BC=AC=12cm
AE是BC的中线,
∴,------------------------9分
∴BD=CE=16cm.---------------------------------10分
25.解:设排球的单价为x元,则篮球的单价为元,根据题意,得
-------------------------------------------3分
解得.-------------------5分
经检验,是原方程的解,且符合题意.------6分
∴.
答:排球的单价为50元,篮球的单价为80元.--------8分
解:(1)△OBC≌△ABD.-----------------------------1分
理由:∵△AOB和△CBD是等边三角形,
∴OB=AB,∠OBA=∠OAB=60°,
BC=BD,∠CBD=60°,-------------------------------2
∴∠OBA+∠ABC=∠CBD+∠ABC,即∠OBC=∠ABD-----------3分
在△OBC和△ABD中,
∴△OBC≌△ABD(SAS).-------------------------------4分
(2)∵△OBC≌△ABD,
∴∠BAD=∠BOC=60°,----------------------------------5分
又∵∠OAB=60°,
∴∠OAE=180°﹣∠OAB﹣∠BAD=60°----------------------6分
∴∠AEO=30°------------------------------------------7分
∴随着点C位置的变化,∠AEO不会发生变化----------------8分
(3)(-2,0)或(6,0).-------------------------------------12分
同课章节目录
