第五章位置的确定 回顾与思考
图片预览



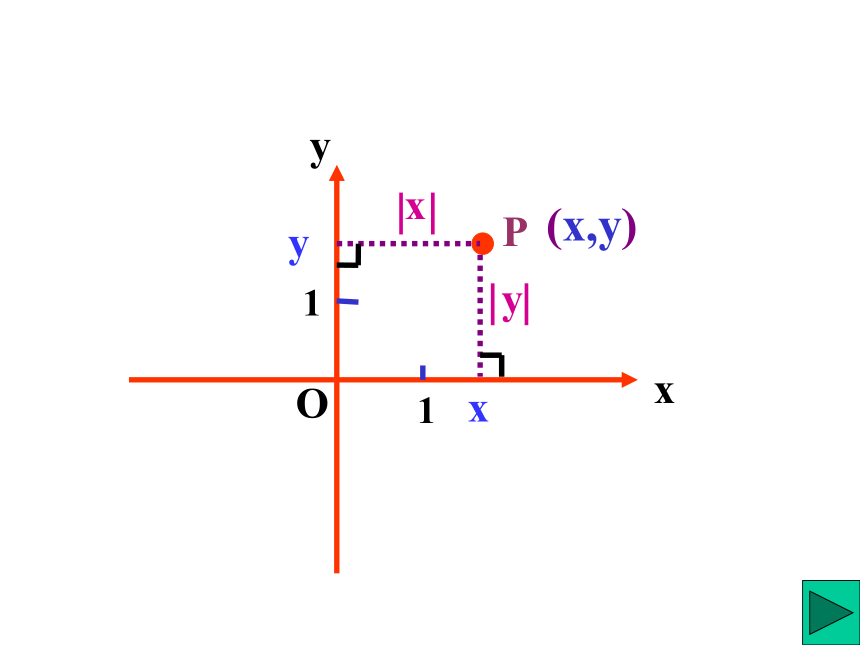


文档简介
(共32张PPT)
第五章 回顾与思考
2012年3月16日
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
复习目标
1.了解在平面内确定点的位置一般需要两个数据并能灵活地运用.
2.认识并能画出平面直角坐标系;在给定的直角坐标系中, 会根据坐标描出点的位置, 由点的位置写出它的坐标.
3.会建立适当的直角坐标系, 描述物体的位置;能结合具体情境灵活运用多种方式确定物体的位置.
4.在同一直角坐标系中, 了解图形变换与点的坐标的变化之间的相互关系.
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
列 表
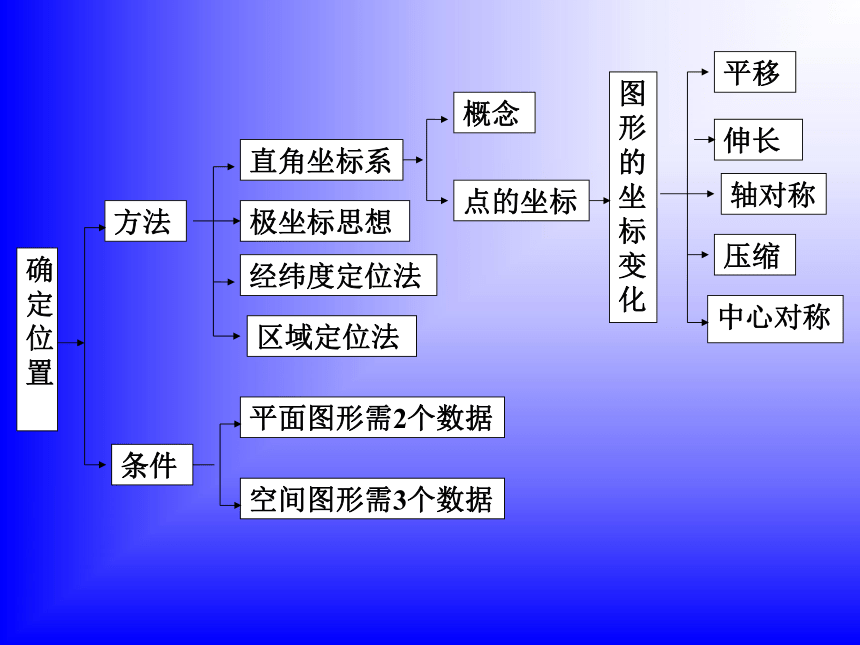
本章知识结构:
确定位置
方法
条件
直角坐标系
极坐标思想
经纬度定位法
区域定位法
平面图形需2个数据
空间图形需3个数据
概念
点的坐标
图
形
的
坐
标
变
化
轴对称
平移
伸长
中心对称
压缩
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
列 表
知识点回顾:
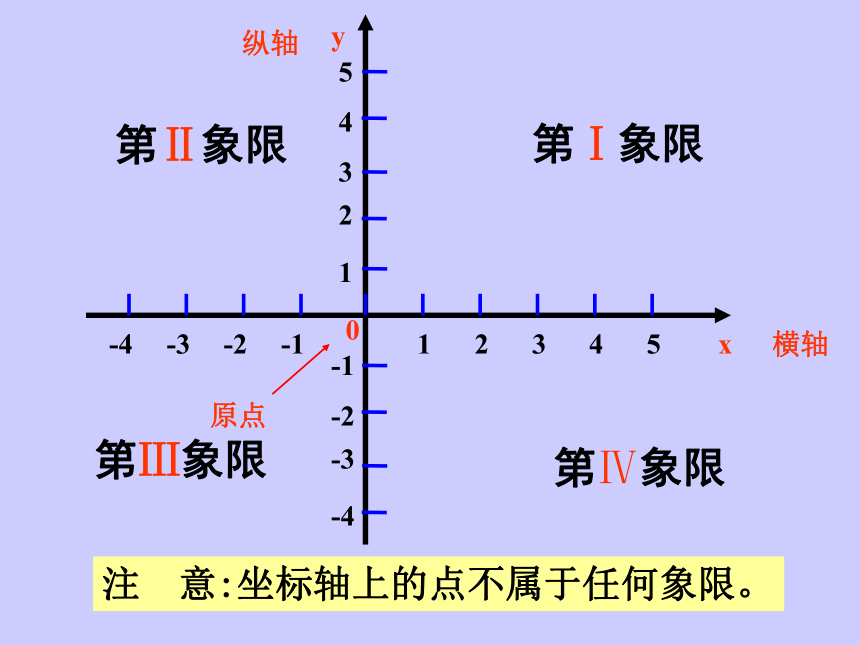
1.什么是平面直角坐标系?
2.两条坐标轴如何称呼,方向如何确定?
3.坐标轴分平面为四部分, 分别叫做什么?
4.什么是点的坐标 平面内点的坐标有几部分组成?
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
第Ⅰ象限
第Ⅳ象限
第Ⅲ象限
第Ⅱ象限
注 意:坐标轴上的点不属于任何象限。
x
y
O
P
1
1
x
y
(x,y)
y
x
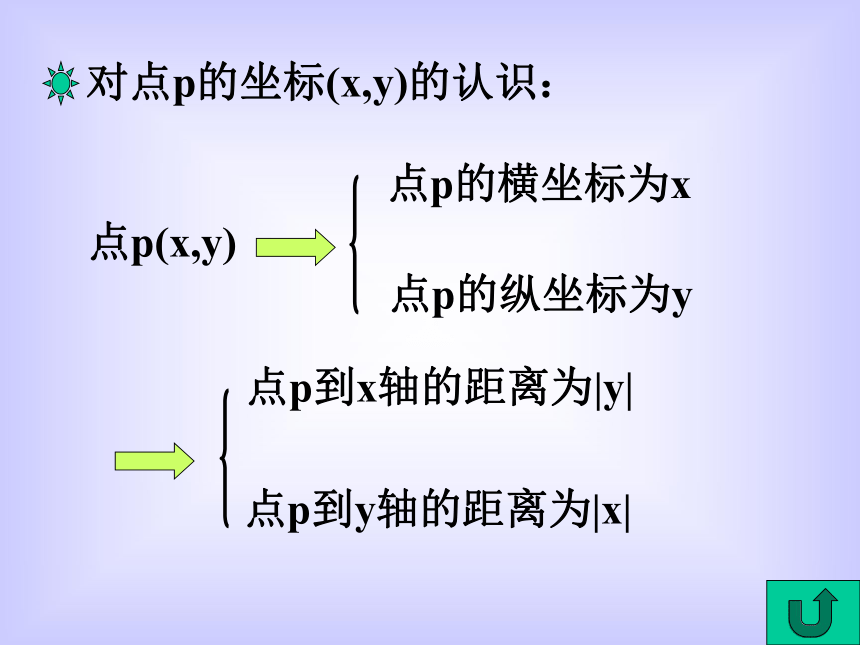
点p的横坐标为x
点p的纵坐标为y
点p到x轴的距离为|y|
点p到y轴的距离为|x|
对点p的坐标(x,y)的认识:
点p(x,y)
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y
·
O
X
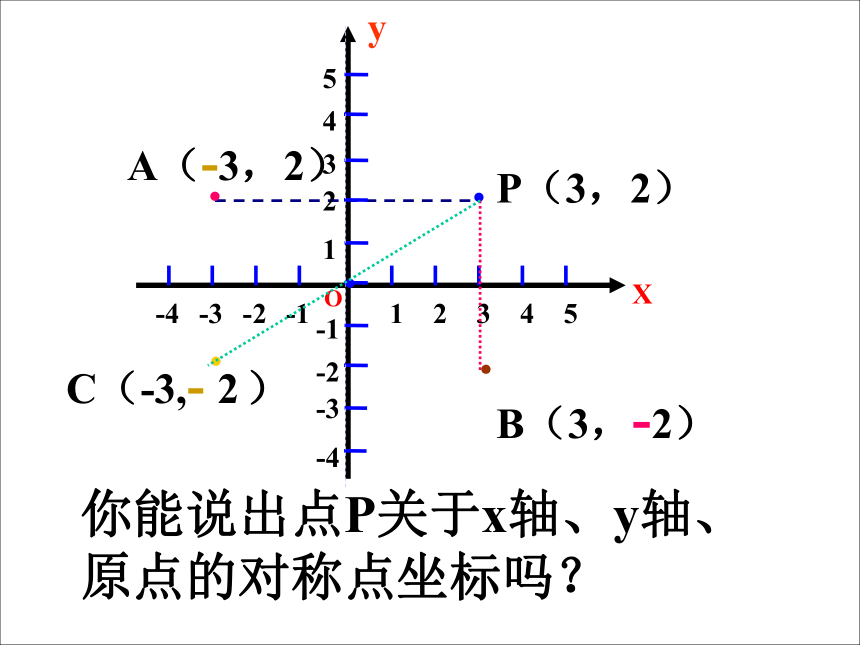
P(3,2)
·
B(3,-2)
A(-3,2)
C(-3,- 2 )
·
·
你能说出点P关于x轴、y轴、原点的对称点坐标吗?
·
一、平移
1.纵坐标不变,横坐标分别增加(减少)a个单位时,图形 平移 a个 单位;
2.横坐标不变,纵坐标分别增加(减少) a个单位时,图形 平移a个单位;
向右(向左)
向上(向下)
二、伸长(压缩)
3.纵坐标不变,横坐标分别变为原来的a倍,则图形 为原来 的a倍(a>1)
4.横坐标不变,纵坐标分别变为原来的a倍,则图形 为原来 的a倍(a>1)
5.横坐标与纵坐标同时变为原来的a倍,则图形
(a>1)
横向伸长
或图形横向缩短为原来的a倍(0纵向伸长
或图形纵向缩短为原来的a倍(0图形被放大,形状不变
三、轴对称
6.纵坐标不变,横坐标分别乘-1,所得图形与
原图形关于 ;
7.横坐标不变,纵坐标分别乘-1,所得图形与
原图形关于 ;
y轴对称
x轴对称
原点
四、中心对称
8.横坐标与纵坐标都乘-1,所得图形与原图形
关于 中心对称。
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
1、如图, 小明家周边地区的平面示意图, 解决如下问题.
(1)书店在小明家 方向, 距离为 米.
(2)某楼位于小明家的南偏东的方向, 到小明家的实际距离约为350米, 这一地点是 .
讲 解
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
讲 解
2、小明将某点关于x轴的对称点误认为是关于y轴的对称点,得到点(-3, -2),求该点坐标及关于x轴、原点的对称点的坐标.
解: 因为小明将所求点误认为是关于y轴的对称点而得到(-3, -2)点, 所以该点是(-3, -2)关于 的对称点;因此由点(-3, -2)可得该点坐标为 ;该点关于x轴的对称点的坐标为 ;关于原点的对称点的坐标为 .
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
讲 解
3、点A(a, b)和B关于x轴对称,而点B与点C(2, 3)关于y轴对称, 那么, a= ___, b= ___ , 点A和C的位置关系是________________.
-2
-3
关于原点对称
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
4、在矩形ABCD中, A点的坐标为(1, 3) , B点坐标为(1, -2), C点坐标为 (-4, -2) ,则D点的坐标是_________ .
讲 解
(-4, 3)
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
5、在直角坐标系中, A(1, 0), B(-1, 0) , △ABC为等腰三角形, 则C点的坐标是______________________ .
讲 解
(0, )或(0, )
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
6、若A(-9,12), 另一点P在x轴上, P到y轴的距离等于A到原点的距离,则P点坐标为_________________ .
讲 解
(15,0)或(-15,0)
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
7、如多边形各个顶点的横坐标保持不变,纵坐标分别乘以-1,那么所得到的图形与原多边形相比的变化是________________;如多边形各个顶点的纵坐标保持不变,横坐标分别乘以-1,那么所得到的图形与原多边形相比的变化是________________ .
讲 解
关于y轴对称
关于x轴对称
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
题 型
1.已知△ABC三顶点坐标分别是A(-7, 0)、B(1, 0)、C(-5, 4), 那么△ABC的面积等于______.
16
2.已知等边△ABC的两个顶点坐标为A(-4, 0)、B(2, 0), 则点C的坐标为_____________________, △ABC的面积为______.
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
3.已知菱形两条对角线的长分别为6和8,建立适当的直角坐标系,写出各顶点的坐标.你的答案是惟一的吗?
题 型
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
达 标
1. 在平面内,确定一个点的位置一般需要的数据个数是( )
A.1 B.2 C.3 D.4
2.下列语句,其中正确的有( )
①点(3, 2)与(2, 3)是同一个点 ②点(0, -2)在x轴上
③点(0, 0)是坐标原点
A.0个 B.1个 C.2个 D.3个
B
B
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
3.已知点M到x轴的距离为3, 到y轴的距离为2,则M点的坐标为
( )
A. (3, 2) B.(-3, -2) C.(3, -2)
D.(2, 3) (2, -3), (-2, 3), (-2, -3)
达 标
D
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
4.在以下四点中,哪一点与点(-3, 4)的连接线段与x轴和y轴都不相交( )
A.(-2,3) B.(2,-3)
C.(2,3) D.(-2,-3)
5.点P(-1, 3)关于原点对称的点的坐标是 ( )
A.(-1,-3) B.(1,-3)
C.(1,3) D.(-3,1)
达 标
A
B
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
6. 一个平行四边形三个顶点的坐标分别是(0, 0)、(2, 0)、(1, 2), 第四个顶点在x轴下方, 则第四个顶点的坐标为( )
A.(-1,-2) B.(1,-2)
C.(3,2) D.(-1,2)
达 标
B
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
归 因
x
O
-4 -3 -2 -1 1 2 3 4
-3
-2
-1
1
4
3
2
-4
y
平面直角坐标系
①两条数轴
②互相垂直
③原点重合
研究对象:
点的坐标
点的位置 横坐标符号 纵坐标符号
第一象限
第二象限
第三象限
第四象限
x轴正半轴上
x轴负半轴上
y轴正半轴上
y轴负半轴上
原点
根据点所在的位置,用+ ,-或0填表
+
+
-
+
-
-
+
-
+
0
-
0
0
+
0
-
0
0
(m,-m)
(m,m)
(-,-)
(-,+)
(+,-)
(+,+)
横坐标相同
纵坐标相同
(0,0)
(0,y)
(x,0)
二四
象限
一三象限
第四象限
第三象限
第二象限
第一象限
平行于y轴
平行于x轴
原点
y轴
x轴
象限角平分线上的点
点P(x,y)在各象限的坐标的符号特点
连线平行于坐标轴的点
坐标轴上点P(x,y)
特殊位置点的特殊坐标:
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
强 化
1.在图中A(2,-4), B(4,-3), C(5,0), 求四边形ABCO的面积。
x
y
D
E
12.5
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
2.如图: 四边形OABC为直角梯形, OA平行于BC, BA 垂直OA于A ,且OA=10, OC=4, ∠AOC=300, 求此梯形的顶点B, C的坐标. 并求出梯形OABC的面积.
O
A
B
C
B( 10, - 2)
C( , -2), S梯形OABC=20-
强 化
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
谈谈收获
对自己说,你有什么收获!
对教师说,你有什么疑惑!
对同学说,你有什么提示!
第五章 回顾与思考
2012年3月16日
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
复习目标
1.了解在平面内确定点的位置一般需要两个数据并能灵活地运用.
2.认识并能画出平面直角坐标系;在给定的直角坐标系中, 会根据坐标描出点的位置, 由点的位置写出它的坐标.
3.会建立适当的直角坐标系, 描述物体的位置;能结合具体情境灵活运用多种方式确定物体的位置.
4.在同一直角坐标系中, 了解图形变换与点的坐标的变化之间的相互关系.
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
列 表
本章知识结构:
确定位置
方法
条件
直角坐标系
极坐标思想
经纬度定位法
区域定位法
平面图形需2个数据
空间图形需3个数据
概念
点的坐标
图
形
的
坐
标
变
化
轴对称
平移
伸长
中心对称
压缩
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
列 表
知识点回顾:
1.什么是平面直角坐标系?
2.两条坐标轴如何称呼,方向如何确定?
3.坐标轴分平面为四部分, 分别叫做什么?
4.什么是点的坐标 平面内点的坐标有几部分组成?
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
第Ⅰ象限
第Ⅳ象限
第Ⅲ象限
第Ⅱ象限
注 意:坐标轴上的点不属于任何象限。
x
y
O
P
1
1
x
y
(x,y)
y
x
点p的横坐标为x
点p的纵坐标为y
点p到x轴的距离为|y|
点p到y轴的距离为|x|
对点p的坐标(x,y)的认识:
点p(x,y)
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y
·
O
X
P(3,2)
·
B(3,-2)
A(-3,2)
C(-3,- 2 )
·
·
你能说出点P关于x轴、y轴、原点的对称点坐标吗?
·
一、平移
1.纵坐标不变,横坐标分别增加(减少)a个单位时,图形 平移 a个 单位;
2.横坐标不变,纵坐标分别增加(减少) a个单位时,图形 平移a个单位;
向右(向左)
向上(向下)
二、伸长(压缩)
3.纵坐标不变,横坐标分别变为原来的a倍,则图形 为原来 的a倍(a>1)
4.横坐标不变,纵坐标分别变为原来的a倍,则图形 为原来 的a倍(a>1)
5.横坐标与纵坐标同时变为原来的a倍,则图形
(a>1)
横向伸长
或图形横向缩短为原来的a倍(0
或图形纵向缩短为原来的a倍(0
三、轴对称
6.纵坐标不变,横坐标分别乘-1,所得图形与
原图形关于 ;
7.横坐标不变,纵坐标分别乘-1,所得图形与
原图形关于 ;
y轴对称
x轴对称
原点
四、中心对称
8.横坐标与纵坐标都乘-1,所得图形与原图形
关于 中心对称。
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
1、如图, 小明家周边地区的平面示意图, 解决如下问题.
(1)书店在小明家 方向, 距离为 米.
(2)某楼位于小明家的南偏东的方向, 到小明家的实际距离约为350米, 这一地点是 .
讲 解
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
讲 解
2、小明将某点关于x轴的对称点误认为是关于y轴的对称点,得到点(-3, -2),求该点坐标及关于x轴、原点的对称点的坐标.
解: 因为小明将所求点误认为是关于y轴的对称点而得到(-3, -2)点, 所以该点是(-3, -2)关于 的对称点;因此由点(-3, -2)可得该点坐标为 ;该点关于x轴的对称点的坐标为 ;关于原点的对称点的坐标为 .
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
讲 解
3、点A(a, b)和B关于x轴对称,而点B与点C(2, 3)关于y轴对称, 那么, a= ___, b= ___ , 点A和C的位置关系是________________.
-2
-3
关于原点对称
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
4、在矩形ABCD中, A点的坐标为(1, 3) , B点坐标为(1, -2), C点坐标为 (-4, -2) ,则D点的坐标是_________ .
讲 解
(-4, 3)
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
5、在直角坐标系中, A(1, 0), B(-1, 0) , △ABC为等腰三角形, 则C点的坐标是______________________ .
讲 解
(0, )或(0, )
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
6、若A(-9,12), 另一点P在x轴上, P到y轴的距离等于A到原点的距离,则P点坐标为_________________ .
讲 解
(15,0)或(-15,0)
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
7、如多边形各个顶点的横坐标保持不变,纵坐标分别乘以-1,那么所得到的图形与原多边形相比的变化是________________;如多边形各个顶点的纵坐标保持不变,横坐标分别乘以-1,那么所得到的图形与原多边形相比的变化是________________ .
讲 解
关于y轴对称
关于x轴对称
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
题 型
1.已知△ABC三顶点坐标分别是A(-7, 0)、B(1, 0)、C(-5, 4), 那么△ABC的面积等于______.
16
2.已知等边△ABC的两个顶点坐标为A(-4, 0)、B(2, 0), 则点C的坐标为_____________________, △ABC的面积为______.
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
3.已知菱形两条对角线的长分别为6和8,建立适当的直角坐标系,写出各顶点的坐标.你的答案是惟一的吗?
题 型
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
达 标
1. 在平面内,确定一个点的位置一般需要的数据个数是( )
A.1 B.2 C.3 D.4
2.下列语句,其中正确的有( )
①点(3, 2)与(2, 3)是同一个点 ②点(0, -2)在x轴上
③点(0, 0)是坐标原点
A.0个 B.1个 C.2个 D.3个
B
B
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
3.已知点M到x轴的距离为3, 到y轴的距离为2,则M点的坐标为
( )
A. (3, 2) B.(-3, -2) C.(3, -2)
D.(2, 3) (2, -3), (-2, 3), (-2, -3)
达 标
D
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
4.在以下四点中,哪一点与点(-3, 4)的连接线段与x轴和y轴都不相交( )
A.(-2,3) B.(2,-3)
C.(2,3) D.(-2,-3)
5.点P(-1, 3)关于原点对称的点的坐标是 ( )
A.(-1,-3) B.(1,-3)
C.(1,3) D.(-3,1)
达 标
A
B
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
6. 一个平行四边形三个顶点的坐标分别是(0, 0)、(2, 0)、(1, 2), 第四个顶点在x轴下方, 则第四个顶点的坐标为( )
A.(-1,-2) B.(1,-2)
C.(3,2) D.(-1,2)
达 标
B
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
归 因
x
O
-4 -3 -2 -1 1 2 3 4
-3
-2
-1
1
4
3
2
-4
y
平面直角坐标系
①两条数轴
②互相垂直
③原点重合
研究对象:
点的坐标
点的位置 横坐标符号 纵坐标符号
第一象限
第二象限
第三象限
第四象限
x轴正半轴上
x轴负半轴上
y轴正半轴上
y轴负半轴上
原点
根据点所在的位置,用+ ,-或0填表
+
+
-
+
-
-
+
-
+
0
-
0
0
+
0
-
0
0
(m,-m)
(m,m)
(-,-)
(-,+)
(+,-)
(+,+)
横坐标相同
纵坐标相同
(0,0)
(0,y)
(x,0)
二四
象限
一三象限
第四象限
第三象限
第二象限
第一象限
平行于y轴
平行于x轴
原点
y轴
x轴
象限角平分线上的点
点P(x,y)在各象限的坐标的符号特点
连线平行于坐标轴的点
坐标轴上点P(x,y)
特殊位置点的特殊坐标:
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
强 化
1.在图中A(2,-4), B(4,-3), C(5,0), 求四边形ABCO的面积。
x
y
D
E
12.5
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
2.如图: 四边形OABC为直角梯形, OA平行于BC, BA 垂直OA于A ,且OA=10, OC=4, ∠AOC=300, 求此梯形的顶点B, C的坐标. 并求出梯形OABC的面积.
O
A
B
C
B( 10, - 2)
C( , -2), S梯形OABC=20-
强 化
列 表
讲 解
题 型
达 标
谈谈收获
复习目标
归 因
强 化
谈谈收获
对自己说,你有什么收获!
对教师说,你有什么疑惑!
对同学说,你有什么提示!
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
