5.2 平面直角坐标（第三课时）

(共30张PPT)
*
5.2 平面直角坐标（第三课时）
预 习
展 示
互 动
生 成
谈谈收获
学习目标
达 标
拓 展
学习目标
1、进一步巩固画平面直角坐标系，在给定的直角坐标系中，会根据坐标轴描出点的位置， 由点的位置写出它的坐标。
2、能在方格纸上建立适当的直角坐标系，描述物体的位置。
3、能结合具体情景灵活运用多种方式确定物体的位置。
预 习
展 示
互 动
生 成
谈谈收获
学习目标
达 标
拓 展
预　习
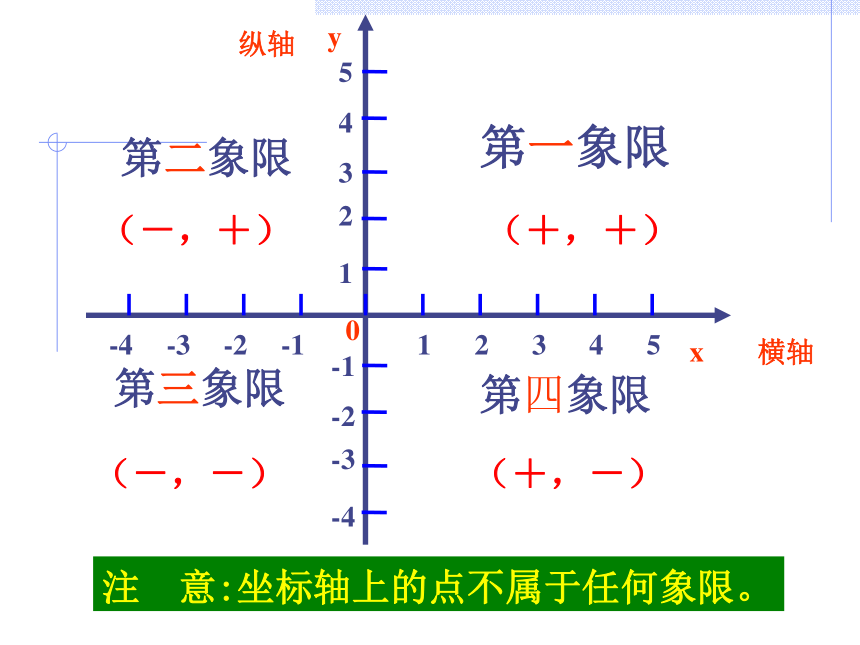
温故知新
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
第一象限
第四象限
第三象限
第二象限
注 意:坐标轴上的点不属于任何象限。
（＋，＋）
（－，＋）
（－，－）
（＋，－）
预 习
展 示
互 动
生 成
谈谈收获
学习目标
达 标
拓 展
展　示
请你来帮忙
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
B
·
A
·
D
·
C
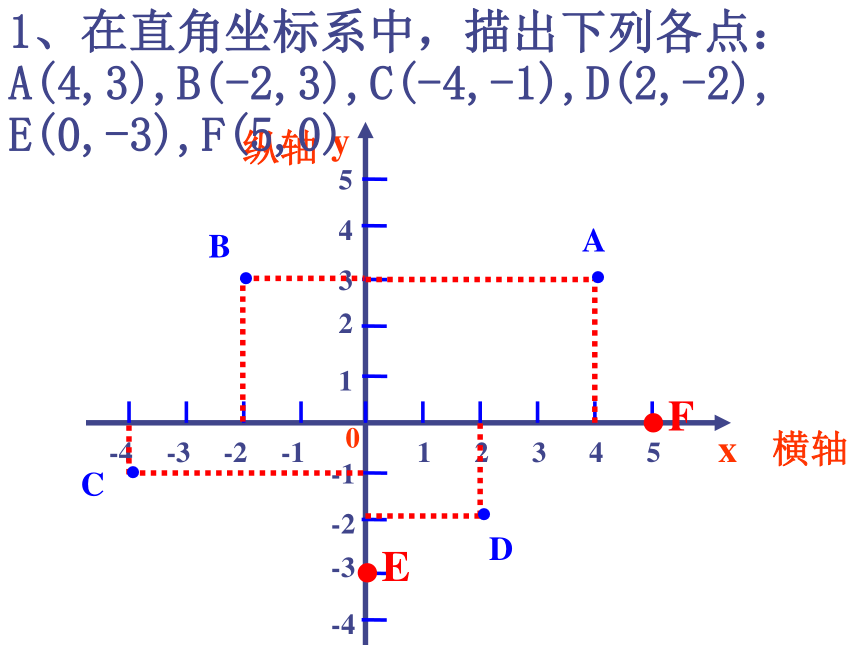
1、在直角坐标系中，描出下列各点：
A(4,3),B(-2,3),C(-4,-1),D(2,-2), E(0,-3),F(5,0)
.E
.F
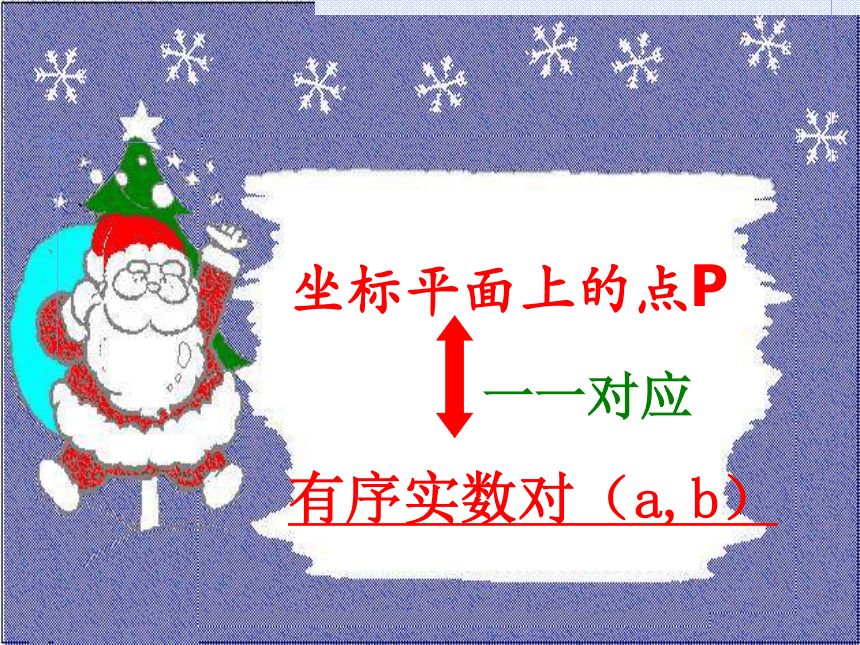
坐标平面上的点P
有序实数对（a,b）
一一对应
-1
o
y
x
-2
-6
2
6
2
6
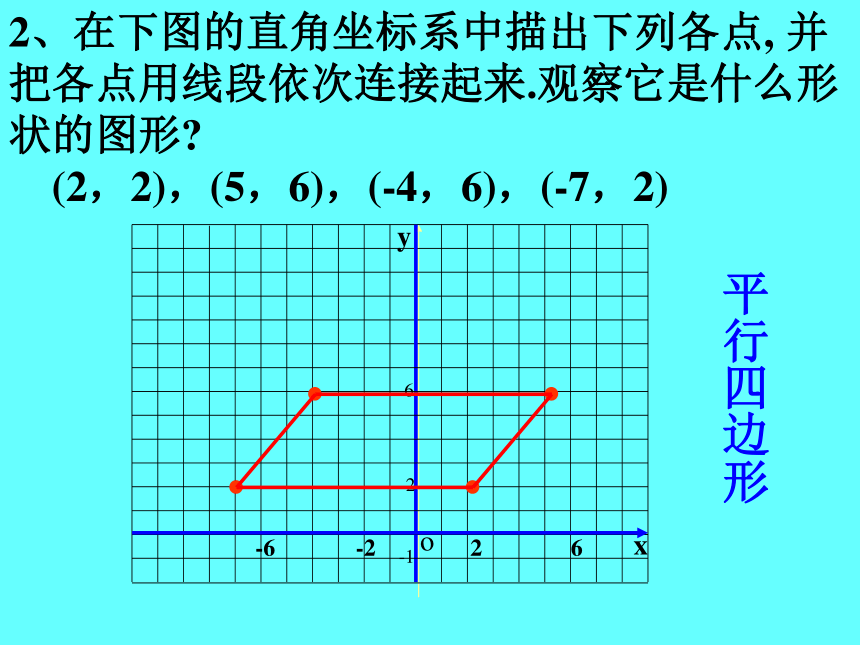
2、在下图的直角坐标系中描出下列各点, 并把各点用线段依次连接起来.观察它是什么形状的图形
(2，2)，(5，6)，(-4，6)，(-7，2)
平行四边形
预 习
展 示
互 动
生 成
谈谈收获
学习目标
达 标
拓 展
互　动
看哪个小组最先完成
例3、请在坐标纸上建立平面直角坐标系，然后描出下列各点.
(1)A(0,5), B(-6,2), C(6,2),
(2)D(-3,2) , E(-3,-2), F(3,-2), G(3,2)
x
B
G
-1
y
A
C
D
E
F
M
N
P
Q
(1)A(0,5) B(-6,2) C(6,2)
(2)D(-3,2) E(-3,-2) F(3,-2)G(3,2)
-1
y
A
C
D
E
F
M
N
P
Q
1、观察点A、M、N的坐标,点P、Q的坐标.那么坐标轴上的点有什么特征？
B
G
-1
y
A
C
D
E
F
M
N
P
Q
2、各点分别到x轴、y轴的距离是多少？
B
G
-1
y
A
C
D
E
F
M
N
P
Q
3、观察点B,C和D,G和E,F.它们的横纵坐标有什么特征.线段BC和EF与x轴位置上有什么关系.
B
G
-1
y
A
C
D
E
F
M
N
P
Q
4、观察点D,E和F,G.它们的横纵坐标有什么特征.线段DE和FG 与y轴位置上有什么关系
B
G
例4:
⑴已知点P1(a, 3)与点P2(-2, b)关于y轴对称，则a=( ), b=( )
⑵已知点P1(a，3)与点P2(-2，b)关于x轴对称，则a=( ),b=( )
⑶已知点P1(a，3)与点P2(-2，b)关于原点对称，则a=( ),b=( )
-3
-3
2
3
-2
2
预 习
展 示
互 动
生 成
谈谈收获
学习目标
达 标
拓 展
生　成
1.平面直角坐标系的概念：
在平面内，两条互相垂直且有公共原点的数轴组成平面直角坐标系，通常两条数轴分别置于水平位置与铅直位置，取向右与向上的方向分别为两条数轴的正方向，水平的数轴叫做x轴或横轴，铅直的数轴叫做y轴或纵轴，两条数轴的交点O称为直角坐标系的原点。
预 习
展 示
互 动
生 成
谈谈收获
学习目标
达 标
拓 展
生　成
说明：两条坐标轴把平面分成四个部分，右上部分叫做第一象限，其他三个部分按逆时针方向依次叫做第二象限，第三象限和第四象限，如图
预 习
展 示
互 动
生 成
谈谈收获
学习目标
达 标
拓 展
生　成
注意：坐标轴上的点不在任何
一个象限内点的坐标
在平面直角坐标系内一点P，过
P向x轴、y轴分别作垂线，垂足
在x轴、y轴上的对应的数a、b
分别叫P点的横坐标和纵坐标，
则有序实数对（a、b）叫做P点
的坐标。
预 习
展 示
互 动
生 成
谈谈收获
学习目标
达 标
拓 展
生　成
说明：①已知坐标平面内的一
个点，可以确定它的坐标.
②已知点的坐标，在平面直角
坐标系中可以描出该点.
③坐标平面内的点与有序实数
对一一对应的。
预 习
展 示
互 动
生 成
谈谈收获
学习目标
达 标
拓 展
达　　标　
1.在 y轴上的点的横坐标是( ),在 x轴上的点的纵坐标是( 　 ). 2.点 A(2,- 3)关 于 x 轴 对 称 的 点 的 坐 标 是( 　　 ). 3.点 B(- 2,1)关 于 y 轴 对 称 的 点 的 坐 标 是( 　　 ) .
0
0
2, 3
-2, 1
预 习
展 示
互 动
生 成
谈谈收获
学习目标
达 标
拓 展
达　　标　
4.点 M(- 8,12)到 x轴的距离是( ),到 y轴的距离是( ).
5.点(4, 3)与点(4, - 3)的关系是( )
A. 关于原点对称 B. 关于 x轴对称 C. 关于 y轴对称 D. 不能构成对称关系
8
12
B
预 习
展 示
互 动
生 成
谈谈收获
学习目标
达 标
拓 展
达　　标　
6.若点 P(2m-1, 3)在第二象限,则( ) A. m>1/2 B. m<1/2
C. m≥-1/2 D. m≤1/2. 7.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
A.平行于 x轴 B.平行于 y轴
C.经过原点 D.以上都不对
B
B
预 习
展 示
互 动
生 成
谈谈收获
学习目标
达 标
拓 展
拓　展
1.若mn=0,则点P(m, n)必定在__________________________上. 2.已知点 P(a,b),Q(3,6)且PQ∥x轴,则 b的值为________ .
3.点(m, -1)和点(2, n)关于x轴对称,则 mn等于( ) A. -2 B. 2 C. 1 D. -1
坐标上或坐标原点
6
A
预 习
展 示
互 动
生 成
谈谈收获
学习目标
达 标
拓 展
拓　展
4.实数x, y满足x2+y2=0, 则点P(x, y)在( ) A. 原点 B. x轴正半轴
C. 第一象限 D. 任意位置 5.点 A 在第一象限,当 m =____时, 点A( m+1, 3m-5)到y轴的距离是它到x轴距离的一半 .
A
7
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
A
B
C
D
能力训练
已知边长为4的正方形 ABCD,在直角坐标系中,C、D两点在第二象限,AB与 X轴的交角为 60°,求C点的坐标.
思考题:
预 习
展 示
互 动
生 成
谈谈收获
学习目标
达 标
拓 展
谈谈收获
对自己说，你有什么收获！
对教师说，你有什么疑惑！
对同学说，你有什么提示！