非线性回归方程的求法

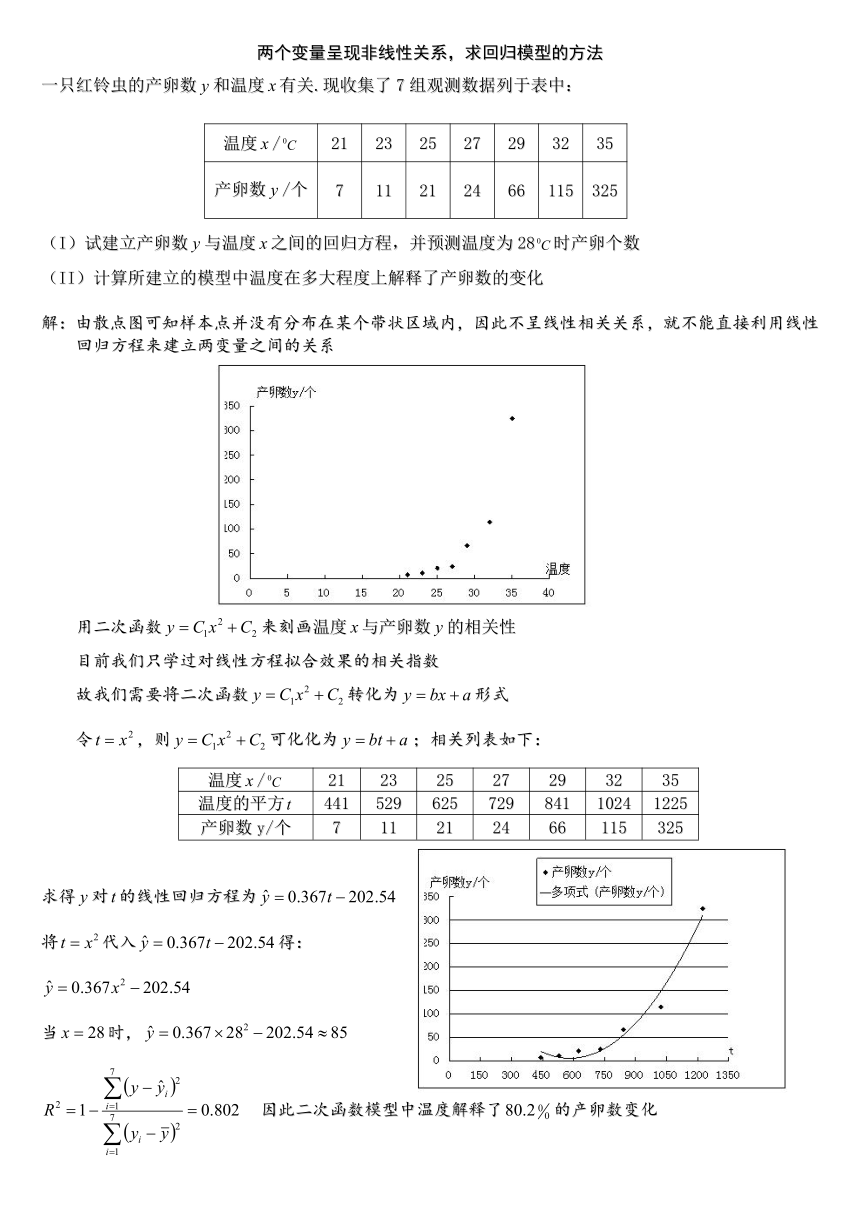
两个变量呈现非线性关系，求回归模型的方法
一只红铃虫的产卵数和温度有关.现收集了7组观测数据列于表中：
温度/ 21 23 25 27 29 32 35
产卵数/个 7 11 21 24 66 115 325
（I）试建立产卵数与温度之间的回归方程，并预测温度为28时产卵个数
（II）计算所建立的模型中温度在多大程度上解释了产卵数的变化
解：由散点图可知样本点并没有分布在某个带状区域内，因此不呈线性相关关系，就不能直接利用线性
回归方程来建立两变量之间的关系
用二次函数来刻画温度与产卵数的相关性
目前我们只学过对线性方程拟合效果的相关指数
故我们需要将二次函数转化为形式
令，则可化化为；相关列表如下：
温度/ 21 23 25 27 29 32 35
温度的平方 441 529 625 729 841 1024 1225
产卵数y/个 7 11 21 24 66 115 325
求得对的线性回归方程为
将代入得：
当时，
因此二次函数模型中温度解释了的产卵数变化
用指数函数来刻画温度与产卵数的相关性
若令可以将转化为形式
对两边取对数
令，， 则有；相关列表如下：
温度/ 21 23 25 27 29 32 35
1.946 2.398 3.405 3.178 4.19 4.745 5.784
产卵数/个 7 11 21 24 66 115 325
求得对的线性回归方程为
将，代入
得：
当时，
利用计算器求得
因此二次函数模型中温度解释了的产卵数变化
综上可得用指数模型拟合效果较好，也就是说刻画产卵数与温度的关系更接近实际情况
1.在回归分析中，代表了数据点和它在回归直线上相应位置的差异的是( )
A.总偏差平方和 B.残差平方和 C.回归平方和 D.相关指数R2
2.回归分析中，相关指数R2的值越大，说明残差平方和( )
A.越小 B.越大 C.可能大也可能小 D.以上都不对
3.若对于变量 ( http: / / www. / )与 ( http: / / www. / )的 ( http: / / www. / )组统计数据的回归模型中，相关指数 ( http: / / www. / )，又知残差平方和为 ( http: / / www. / )，那么 ( http: / / www. / )的值为（ ） （A) ( http: / / www. / ) （B） ( http: / / www. / ) （C） ( http: / / www. / ) （D） ( http: / / www. / )
0.25 0.5 1 2 4
16 12 5 2 1
4.在一次抽样调查中测得样本的5个样本点，数据如下：
（1）画出散点图；（2）通过作出的散点图发现，与之
间的关系可用函数拟合，试确定的值