(小升初真题专项)六年级数学找规律题(易错题、难题)名师详解连载二
文档属性
| 名称 | (小升初真题专项)六年级数学找规律题(易错题、难题)名师详解连载二 |  | |
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 15:03:58 | ||
图片预览




文档简介
(小升初真题)六年级数学找规律题(易错题、难题)名师详解连载二
1,有一列数:2,5,8,11.14,…,104在这列数中是第(?)个数。
A.33 B.34 C.35 D.36
2.右边的算式中,四个小纸片各覆盖住一个数字,被覆盖住的两个两位数的和是(?)。
A.26 B.28 C.23或15 D.27或28
3.如图,用同样大小的黑色棋子按如图所示的规律摆放:
……
① ② ③ ④
则第2017个图案有( )颗黑色棋子。
4.如图,用同样大小的黑色棋子按如图所示的规律摆放:
则第2017个图案有( )颗黑色棋子。
5.乐乐把黑、白两种棋子叠成了几堆,右面是分别从上面、前面和左面观察到的图形,这几堆棋子一共有( )枚。
1.现有若干个圆环,它的外直径是5厘米,环宽是0.5厘米,将它们(如下图)扣在一起,拉紧后测量其长度,请完成表格。(6分)
圆环个数 1 2 3 4 5 6 ……
拉紧后的长度/cm
根据表中规律,11个圆环拉紧后的长度是多少厘米?
设圆环的个数为a?,拉紧后的总长度为S,你能用一个关系式表示你发现的规律吗?
若拉紧后的长度是77厘来,则它是由多少个圆环扣成的?
2.如图所示,用“十字形”分割正方形,分割1次,分成了4个正方形;分割2次分成了7个正方形;分割3次分成了10个正方形……以此类推,请填写下表。
分割次数 1 2 3 4 5 …
正方形总个数 4 7 10
…
分割次数 1 2 3 4 5 …
正方形总个数 4 7 10
…
分割次数 1 2 3 4 5 …
正方形总个数 4 7 10
…
分割次数 1 2 3 4 5 …
正方形总个数 4 7 10
…
(1)如果连续用“十字形”分割18次,则可以分成______个正方形。
(2)如果分割了286个正方形,共用“十字形”分割了 次。
巧算“24”点。7,8,9,10 3,3,7,7 。
在,,,,,,……第10个数为( )。
已知一串分数;,;,,;,,,;……
(1)是此串分数中的第(? )个分数:
(2)第115个分数是( ?)。
4.如图所示:
在平面内画1个圆可以将平面分成2个部分,在平面内画2个圆最多可以将平面分成4个部分。
(1)在平面内画3个圆最多可以将平面分成(? ?)个部分;?(1分)
(2)在平面内画4个圆最多可以将平面分成(? )个部分;?(2分)
(3)在平面内画n个圆最多可以将平面分成(? )个部分;?(2分)
观察算式:2?-1?=3,3?-2?=5,5?-4?=9……那么22?-(? )=(? ),
n?-( )?=( )
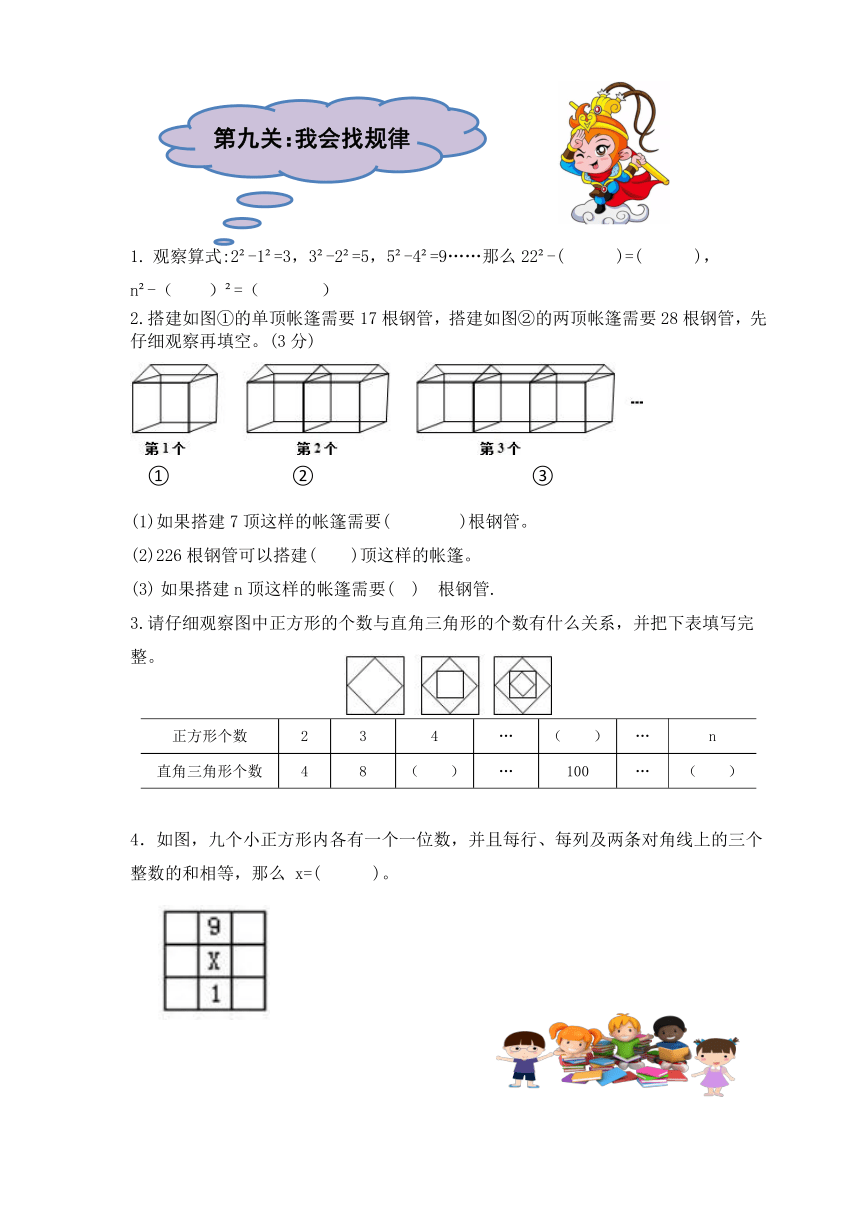
2.搭建如图①的单顶帐篷需要17根钢管,搭建如图②的两顶帐篷需要28根钢管,先仔细观察再填空。(3分)
① ② ③
(1)如果搭建7顶这样的帐篷需要( ?)根钢管。
(2)226根钢管可以搭建(??)顶这样的帐篷。
如果搭建n顶这样的帐篷需要(?)?根钢管.
3.请仔细观察图中正方形的个数与直角三角形的个数有什么关系,并把下表填写完整。
正方形个数 2 3 4 … ( ) … n
直角三角形个数 4 8 ( ) … 100 … ( )
4.如图,九个小正方形内各有一个一位数,并且每行、每列及两条对角线上的三个整数的和相等,那么 x=( ?)。
1.3×3×…×3-1的个位数是( )。
2016个
2.将 1 至 9 这九个数分别填在下面九个方框中,使等式成立:
□□×□□=□□×□□□=4234,这三个两位数中最大的一个是( )。
3.200 个连续自然数的和是 32300,取出其中所有的偶数个数(第 2 个,第 4 个,
……,第 200个),将它们相加,则和是( )。
4.小明按照如图的方式用蓝色和白色正方形摆图形。
(1)当中间摆20个蓝色正方形时,四周共需要摆( )个白色正方形。(1分)
(2)如果中间摆n个蓝色正方形,四周共需要摆( )个白色正方形。(1分)
5.如图,将 1.8,5.6,4.7,2.8,6.9 分别填在五个○内,再在每个□中填上和它相连的三个○中的数的平均值,再把三个□中的数的平均值填在△中,找出一种填法,使三角内的数尽可能大,那么△中填的数是多少? (4分)
参考答案及难题详解
第六关
1.B
[分析]根据题意可知两个两位数相乘的积是195?,并且积的个位数字是5?,因为3×5=15?,所以这两个因数的个位数字分别是3和5?,则这两个数是13和15,然后把它们相加即可.
详解:13×15=195 13+15=28, 故答案为:?B.
2.C
详解:(104-2)÷3+1=102÷3+1=34+1=35. 故答案为:35.
3.解答
观察图形知:
第1个图形有3+1=4个棋子,第2个图形有3×2+1=7个棋子,
第3个图形有3×3+1=10个棋子,第4个图形有3×4+1=13个棋子,
第n个图形有3n+1个棋子,
当n=2017时,3×2017+1=6052个,故答案为:?6052
解答
观察图形知:
第1个图形有3×(1-1)+1=1个棋子,第2个图形有3×(2-1)+1=4个棋子,第3个图形有3×(3-1)+1=7个棋子,第4个图形有3×(4-1)+1=10个棋子,第5个图形有3×(5-1)+1=13个棋子,
第n个图形有3(n-1)+1个棋子,
当n=2017时,3×(2017-1)+1=6049个,故答案为:6049.
13. 解析
2排:第一排,是 6+4=10(枚),第二排 ,是3枚。这几堆棋子一共有(10+3=13)枚。
第七关
1.?(1)?1+4×11=45(厘米)?(2)S=1+4a (3)(77-1)÷4=19(个)
2. 13 16 (1)55 (2)95
分析:
根据题干分割1次,得到4个正方形,可以写成1+1×3个;分割2次得到7个正方形,可写成1+2×3个…由此可得每分割一次就增加3个正方形,由此可得,分割n次,得到1+3n个正方形,由此即可解决问题.
解答:
分割1?次,得到4?个正方形,可以写成1+1×3?个;分割2?次得到7?个正方形,可写成1+2×3?个…?由此可得每分割一次就增加3?个正方形,
由此可得,分割n?次,得到1+3n?个正方形,
当n=18?时,?正方形的个数为:1+18×3=55(?个)?
1+3n=286,n=95
第八关
巧算“24”点。
7,8,9,10 9÷(10-7)×8 =24
3,3,7,7 (3+)×7=24
2.在,,,,,,……第10个数为( )。
因为= , = ,所以原题改为:
在,,,,,,……第10个数为( )
分子1,3,5,7,9,11……;分母3,6,9,12,15,18……
3.1231;
解析
(1)观察给出的数列知道,分母是1的分数有1个,分母是2的分数有2个,分母是3的分数有3个……分母是n的分数有n个,由此知道根据等差数列前n项的和n(n+1)÷2,求出1到49的和,进而求出是此串分数中的第几个分数;
(2)根据等差数列前n项的和n(n+1)÷2先求出和为120是此串分数中的第几个分数,进而求出第115个分数是几。
详解(1)从1到分母49/49的数 :::::: 1+2+3+…+49=49×(49+1)÷2=1225 ,也就是说第1225个分数是,往后推7个分数就是, 1225+7=1232。所以是此串分数中的第1232个分数。
n(n+1)÷2=120,
即n(n+1)=240,
因为15×16=240,
所以n=15,
也就是说,第120个数是,往前推,115个分数是。
4.8;14;(n-1)× n+2
详解:在同一个平面内,1个圆把平面分成0×1+2=2,
2个圆把平面最多分成1×2+2=4个部分,
3个圆把平面最多分成2×3+2=8个部分,
4个圆把平面最多分成3×4+2=14个部分,
那么n个圆把平面最多分成(n-1)× n+2个部分?
第九关
1.21? 43? n-1?2n-1
详解:
观察算式:2?-1?=3,3?-2?=5,5?-4?=9……,得出规律:
2?-1?=3=2+1,3?-2?=5=3+2,5?-4?=9=5+4……
那么22?-(21)?=22+21=43,n?-(n-1)?=2n-1
2.(1)第一顶帐篷用钢管数为17根;
搭建二顶帐篷用钢管数为17+11×1=28根;
搭建三顶帐篷用钢管数为17+11×2=39根;
以此类推,七顶帐篷用钢管数为17+11×6=83根
……
搭建n顶帐篷用钢管数为17+11×(n-1)=11n+6根;
(2)20 ,11n+6=226,n=20
(3)11n+6
3.
正方形个数 2 3 4 … (26) … n
直角三角形个数 4 8 (12) … 100 … 4×( n -1)
4.. x=5
如图所示,a+x+f=9+x+1,有 a+f=10;同理 d+x+c=9+x+1 得 d+c=10;
所以 a+f+d+c=20
又 a+9+d=9+x+1,得 a+d=x+1;
c+1+f=9+x+1,得 c+f==x+9,
则 a+d+c+f=2x+10.
所以 2x+10=20,x=5
第十关
1.解析
1个是3的个位是3,3×3=9,个位是9,
3×3×3=27,个位是7,?3×3×3×3=81,?个位是1,3×3×3×3×3=243,?个位是3,得出结论:个位数以3、9、7、1循环;用2016除以4,得到余数,就是知道2016个3相乘的个位数为多少,然后计算即可。
详解
n个3相乘,个位数的规律为:?3、9、7、1循环,
2016÷4=504,没有余数,所以2016个3相乘个位数字是1,
即 3×3×…×3-1 的个位数为:?1-1=0
2016个
2016个-1的个位数是0,故选A。
2.73
分析:把 4234 分解质因数,然后进行计算和调整,有:4234=2×29×73=58×73=29×146,所以最大的两位数是 73。
3.16200
分析:连续自然数相邻两数之差是 1,所以第 2 个数比第 1 个数大 1,第 4 个数比第 3 个数大 1,…,第 200个数比第 199 个数大 1,100 个取出的数比没取出的 100 个数总共多 100,因此所有的第偶数个数之和是
(32300+100)÷2=16200
4.蓝色=1时,白色2×1+6=8; n=2时,白色2×2+6=10;
蓝色=3时,白色2×3+6=12; n=4时,白色2×4+6=14;
……
蓝色=20时,白色2×20+6=46
……
蓝色=n时,白色2×n+6=2n+6
5.△中填 5.1
要使三角中的数尽可能大,就要使三个方框中的三个数的和尽可能大.为了便于说明,不妨设五个○中的数依次为 a、 b、 c、 d、 e,三个□中的数依次为 x、y、z,△中的数为 A.则有
3x=a+b+c,3y=b+c+d,3z=c+d+e 三个□里的数的 3 倍之和,中间○中 c 算了 3 次,两端○中的 a、e 各算 1 次,其余两个数各算 2 次,应将最大数放在中间○内,把最小和次小的数填在两端○内,剩下的两个数放在剩下的○内.所以 3x+3y+3z=6.9×3+5.6×2+4.7×2+1.8+2.8=45.9
x+y+z=45.9÷3=15.3
A=(x+y+z)÷3=15.3÷3=5.1
1,有一列数:2,5,8,11.14,…,104在这列数中是第(?)个数。
A.33 B.34 C.35 D.36
2.右边的算式中,四个小纸片各覆盖住一个数字,被覆盖住的两个两位数的和是(?)。
A.26 B.28 C.23或15 D.27或28
3.如图,用同样大小的黑色棋子按如图所示的规律摆放:
……
① ② ③ ④
则第2017个图案有( )颗黑色棋子。
4.如图,用同样大小的黑色棋子按如图所示的规律摆放:
则第2017个图案有( )颗黑色棋子。
5.乐乐把黑、白两种棋子叠成了几堆,右面是分别从上面、前面和左面观察到的图形,这几堆棋子一共有( )枚。
1.现有若干个圆环,它的外直径是5厘米,环宽是0.5厘米,将它们(如下图)扣在一起,拉紧后测量其长度,请完成表格。(6分)
圆环个数 1 2 3 4 5 6 ……
拉紧后的长度/cm
根据表中规律,11个圆环拉紧后的长度是多少厘米?
设圆环的个数为a?,拉紧后的总长度为S,你能用一个关系式表示你发现的规律吗?
若拉紧后的长度是77厘来,则它是由多少个圆环扣成的?
2.如图所示,用“十字形”分割正方形,分割1次,分成了4个正方形;分割2次分成了7个正方形;分割3次分成了10个正方形……以此类推,请填写下表。
分割次数 1 2 3 4 5 …
正方形总个数 4 7 10
…
分割次数 1 2 3 4 5 …
正方形总个数 4 7 10
…
分割次数 1 2 3 4 5 …
正方形总个数 4 7 10
…
分割次数 1 2 3 4 5 …
正方形总个数 4 7 10
…
(1)如果连续用“十字形”分割18次,则可以分成______个正方形。
(2)如果分割了286个正方形,共用“十字形”分割了 次。
巧算“24”点。7,8,9,10 3,3,7,7 。
在,,,,,,……第10个数为( )。
已知一串分数;,;,,;,,,;……
(1)是此串分数中的第(? )个分数:
(2)第115个分数是( ?)。
4.如图所示:
在平面内画1个圆可以将平面分成2个部分,在平面内画2个圆最多可以将平面分成4个部分。
(1)在平面内画3个圆最多可以将平面分成(? ?)个部分;?(1分)
(2)在平面内画4个圆最多可以将平面分成(? )个部分;?(2分)
(3)在平面内画n个圆最多可以将平面分成(? )个部分;?(2分)
观察算式:2?-1?=3,3?-2?=5,5?-4?=9……那么22?-(? )=(? ),
n?-( )?=( )
2.搭建如图①的单顶帐篷需要17根钢管,搭建如图②的两顶帐篷需要28根钢管,先仔细观察再填空。(3分)
① ② ③
(1)如果搭建7顶这样的帐篷需要( ?)根钢管。
(2)226根钢管可以搭建(??)顶这样的帐篷。
如果搭建n顶这样的帐篷需要(?)?根钢管.
3.请仔细观察图中正方形的个数与直角三角形的个数有什么关系,并把下表填写完整。
正方形个数 2 3 4 … ( ) … n
直角三角形个数 4 8 ( ) … 100 … ( )
4.如图,九个小正方形内各有一个一位数,并且每行、每列及两条对角线上的三个整数的和相等,那么 x=( ?)。
1.3×3×…×3-1的个位数是( )。
2016个
2.将 1 至 9 这九个数分别填在下面九个方框中,使等式成立:
□□×□□=□□×□□□=4234,这三个两位数中最大的一个是( )。
3.200 个连续自然数的和是 32300,取出其中所有的偶数个数(第 2 个,第 4 个,
……,第 200个),将它们相加,则和是( )。
4.小明按照如图的方式用蓝色和白色正方形摆图形。
(1)当中间摆20个蓝色正方形时,四周共需要摆( )个白色正方形。(1分)
(2)如果中间摆n个蓝色正方形,四周共需要摆( )个白色正方形。(1分)
5.如图,将 1.8,5.6,4.7,2.8,6.9 分别填在五个○内,再在每个□中填上和它相连的三个○中的数的平均值,再把三个□中的数的平均值填在△中,找出一种填法,使三角内的数尽可能大,那么△中填的数是多少? (4分)
参考答案及难题详解
第六关
1.B
[分析]根据题意可知两个两位数相乘的积是195?,并且积的个位数字是5?,因为3×5=15?,所以这两个因数的个位数字分别是3和5?,则这两个数是13和15,然后把它们相加即可.
详解:13×15=195 13+15=28, 故答案为:?B.
2.C
详解:(104-2)÷3+1=102÷3+1=34+1=35. 故答案为:35.
3.解答
观察图形知:
第1个图形有3+1=4个棋子,第2个图形有3×2+1=7个棋子,
第3个图形有3×3+1=10个棋子,第4个图形有3×4+1=13个棋子,
第n个图形有3n+1个棋子,
当n=2017时,3×2017+1=6052个,故答案为:?6052
解答
观察图形知:
第1个图形有3×(1-1)+1=1个棋子,第2个图形有3×(2-1)+1=4个棋子,第3个图形有3×(3-1)+1=7个棋子,第4个图形有3×(4-1)+1=10个棋子,第5个图形有3×(5-1)+1=13个棋子,
第n个图形有3(n-1)+1个棋子,
当n=2017时,3×(2017-1)+1=6049个,故答案为:6049.
13. 解析
2排:第一排,是 6+4=10(枚),第二排 ,是3枚。这几堆棋子一共有(10+3=13)枚。
第七关
1.?(1)?1+4×11=45(厘米)?(2)S=1+4a (3)(77-1)÷4=19(个)
2. 13 16 (1)55 (2)95
分析:
根据题干分割1次,得到4个正方形,可以写成1+1×3个;分割2次得到7个正方形,可写成1+2×3个…由此可得每分割一次就增加3个正方形,由此可得,分割n次,得到1+3n个正方形,由此即可解决问题.
解答:
分割1?次,得到4?个正方形,可以写成1+1×3?个;分割2?次得到7?个正方形,可写成1+2×3?个…?由此可得每分割一次就增加3?个正方形,
由此可得,分割n?次,得到1+3n?个正方形,
当n=18?时,?正方形的个数为:1+18×3=55(?个)?
1+3n=286,n=95
第八关
巧算“24”点。
7,8,9,10 9÷(10-7)×8 =24
3,3,7,7 (3+)×7=24
2.在,,,,,,……第10个数为( )。
因为= , = ,所以原题改为:
在,,,,,,……第10个数为( )
分子1,3,5,7,9,11……;分母3,6,9,12,15,18……
3.1231;
解析
(1)观察给出的数列知道,分母是1的分数有1个,分母是2的分数有2个,分母是3的分数有3个……分母是n的分数有n个,由此知道根据等差数列前n项的和n(n+1)÷2,求出1到49的和,进而求出是此串分数中的第几个分数;
(2)根据等差数列前n项的和n(n+1)÷2先求出和为120是此串分数中的第几个分数,进而求出第115个分数是几。
详解(1)从1到分母49/49的数 :::::: 1+2+3+…+49=49×(49+1)÷2=1225 ,也就是说第1225个分数是,往后推7个分数就是, 1225+7=1232。所以是此串分数中的第1232个分数。
n(n+1)÷2=120,
即n(n+1)=240,
因为15×16=240,
所以n=15,
也就是说,第120个数是,往前推,115个分数是。
4.8;14;(n-1)× n+2
详解:在同一个平面内,1个圆把平面分成0×1+2=2,
2个圆把平面最多分成1×2+2=4个部分,
3个圆把平面最多分成2×3+2=8个部分,
4个圆把平面最多分成3×4+2=14个部分,
那么n个圆把平面最多分成(n-1)× n+2个部分?
第九关
1.21? 43? n-1?2n-1
详解:
观察算式:2?-1?=3,3?-2?=5,5?-4?=9……,得出规律:
2?-1?=3=2+1,3?-2?=5=3+2,5?-4?=9=5+4……
那么22?-(21)?=22+21=43,n?-(n-1)?=2n-1
2.(1)第一顶帐篷用钢管数为17根;
搭建二顶帐篷用钢管数为17+11×1=28根;
搭建三顶帐篷用钢管数为17+11×2=39根;
以此类推,七顶帐篷用钢管数为17+11×6=83根
……
搭建n顶帐篷用钢管数为17+11×(n-1)=11n+6根;
(2)20 ,11n+6=226,n=20
(3)11n+6
3.
正方形个数 2 3 4 … (26) … n
直角三角形个数 4 8 (12) … 100 … 4×( n -1)
4.. x=5
如图所示,a+x+f=9+x+1,有 a+f=10;同理 d+x+c=9+x+1 得 d+c=10;
所以 a+f+d+c=20
又 a+9+d=9+x+1,得 a+d=x+1;
c+1+f=9+x+1,得 c+f==x+9,
则 a+d+c+f=2x+10.
所以 2x+10=20,x=5
第十关
1.解析
1个是3的个位是3,3×3=9,个位是9,
3×3×3=27,个位是7,?3×3×3×3=81,?个位是1,3×3×3×3×3=243,?个位是3,得出结论:个位数以3、9、7、1循环;用2016除以4,得到余数,就是知道2016个3相乘的个位数为多少,然后计算即可。
详解
n个3相乘,个位数的规律为:?3、9、7、1循环,
2016÷4=504,没有余数,所以2016个3相乘个位数字是1,
即 3×3×…×3-1 的个位数为:?1-1=0
2016个
2016个-1的个位数是0,故选A。
2.73
分析:把 4234 分解质因数,然后进行计算和调整,有:4234=2×29×73=58×73=29×146,所以最大的两位数是 73。
3.16200
分析:连续自然数相邻两数之差是 1,所以第 2 个数比第 1 个数大 1,第 4 个数比第 3 个数大 1,…,第 200个数比第 199 个数大 1,100 个取出的数比没取出的 100 个数总共多 100,因此所有的第偶数个数之和是
(32300+100)÷2=16200
4.蓝色=1时,白色2×1+6=8; n=2时,白色2×2+6=10;
蓝色=3时,白色2×3+6=12; n=4时,白色2×4+6=14;
……
蓝色=20时,白色2×20+6=46
……
蓝色=n时,白色2×n+6=2n+6
5.△中填 5.1
要使三角中的数尽可能大,就要使三个方框中的三个数的和尽可能大.为了便于说明,不妨设五个○中的数依次为 a、 b、 c、 d、 e,三个□中的数依次为 x、y、z,△中的数为 A.则有
3x=a+b+c,3y=b+c+d,3z=c+d+e 三个□里的数的 3 倍之和,中间○中 c 算了 3 次,两端○中的 a、e 各算 1 次,其余两个数各算 2 次,应将最大数放在中间○内,把最小和次小的数填在两端○内,剩下的两个数放在剩下的○内.所以 3x+3y+3z=6.9×3+5.6×2+4.7×2+1.8+2.8=45.9
x+y+z=45.9÷3=15.3
A=(x+y+z)÷3=15.3÷3=5.1
同课章节目录
