重庆第八高级中学校2022届高三上学期7月月考(一)数学试题(艺术班) Word版含答案
文档属性
| 名称 | 重庆第八高级中学校2022届高三上学期7月月考(一)数学试题(艺术班) Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 352.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 10:51:08 | ||
图片预览



文档简介
重庆第八高级中学校2022届高三上学期7月月考(一)
数学试题(艺术班)
选择题:本题共8小题,每小题5分,共40分。在每小题列出的的四个选项中,只有一项是符合题目要求的。
1.设集合false,false,则false=( )
A.false B.false C.false D.false
2.复数false的共轭复数是( )
A.false B.false C.false D.false
3.若圆台下底半径为false,上底半径为false,母线长为false,则其体积为( )
A.false B.false C.false D.false
4.设函数false,下列结论中正确的是( )
A.false的最大值等于false
B.false的图象关于直线false对称
C.false在区间false上单调递增
D.false的图象关于点false对称
5.已知直线false过点false,且在两坐标轴上的截距互为相反数,则直线false的方程为( )
A.false B.false或false
C.false或false D.false或false
6.已知false,则false( )
A.false B.false C.false D.false
7.一组样本容量为false的样本数据构成一个公差不为false的等差数列false,若false,且false成等比数列,则此样本数据的平均数和中位数分别是( )
A.false B.false C.false D.false
8.若直线false与曲线false和圆false都相切,则false的方程为( )
A.false B.false C.false D.false
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
9.某中学高一年级有false个班,每班false人;高二年级有false个班,每班false人甲就读于高一,乙就读于高二学校计划从这两个年级中共抽取false人进行视力调查,下列说法中正确的有( )
A.应该采用分层随机抽样法
B.高一、高二年级应分别抽取false人和false人
C.乙被抽到的可能性比甲大
D.该问题中的总体是高一、高二年级的全体学生的视力
10.已知向量false,则( )
A.若false与false垂直,则false
B.若false,则false的值为
C.若false,则false
D.若false,则false与false的夹角为false
11.已知false是两条不同的直线,false是两个不同的平面,有下列命题正确的是( )
A.若false,则false
B.若false,则false
C.若false,则false
D.若false,则false
12.已知圆false,直线false,则下列正确的是( )
A.直线false恒过定点false
B.当false时,圆false上有且仅有三个点到直线false的距离都等于1
C.圆false与曲线false恰有三条公切线,则false
D.当false时,直线false上一个动点false向圆false引两条切线false,其中false为切点,则直线false经过点 false
三、填空题:本题共4小题,每小题5分,共20分。
13.已知false是等差数列,若false,则false____________;
14.若两条直线false和false互相垂直,则false的值为____________;
15.某群体中的每位成员使用移动支付的概率都为false,各成员的支付方式相互独立.设false为该群体的10位成员中使用移动支付的人数,false,则false____________;
16.函数false的单调减区间为____________;若函数false在false上在取得最小值false,则实数a的取值范围是____________.
四.解答题:本题共6小题,共70分. 解答应写出必要文字说明、证明过程或演算步骤。
17.已知等差数列false是递增数列,且false.
(1)求数列false的通项公式;
(2)若false,求数列false的前false项和false.
18.某校为了解“准高三”学生的数学成绩情况,从一次模拟考试中随机抽取了false名学生的数学成绩如下:
78? 64 ? 88? 104? 53? 82? 86? 93? 90? 105? 77? 92? 116
81? 60? 82? 74? 105? 91? 103? 78 88 107? 82? 71
(1)完成这false名学生的数学成绩的茎叶图如图;
(2)确定该样本的中位数和众数;
(3)规定数学成绩不低于false分为“及格”,从该样本“及格”的学生中任意抽出false名,设抽到成绩在区间false的学生人数为false,求false的分布列和数学期望false.
19.在false中,内角false所对的边分别为false,已知false.
(1)求角false的大小;
(2)若false,求false的面积的最大值.
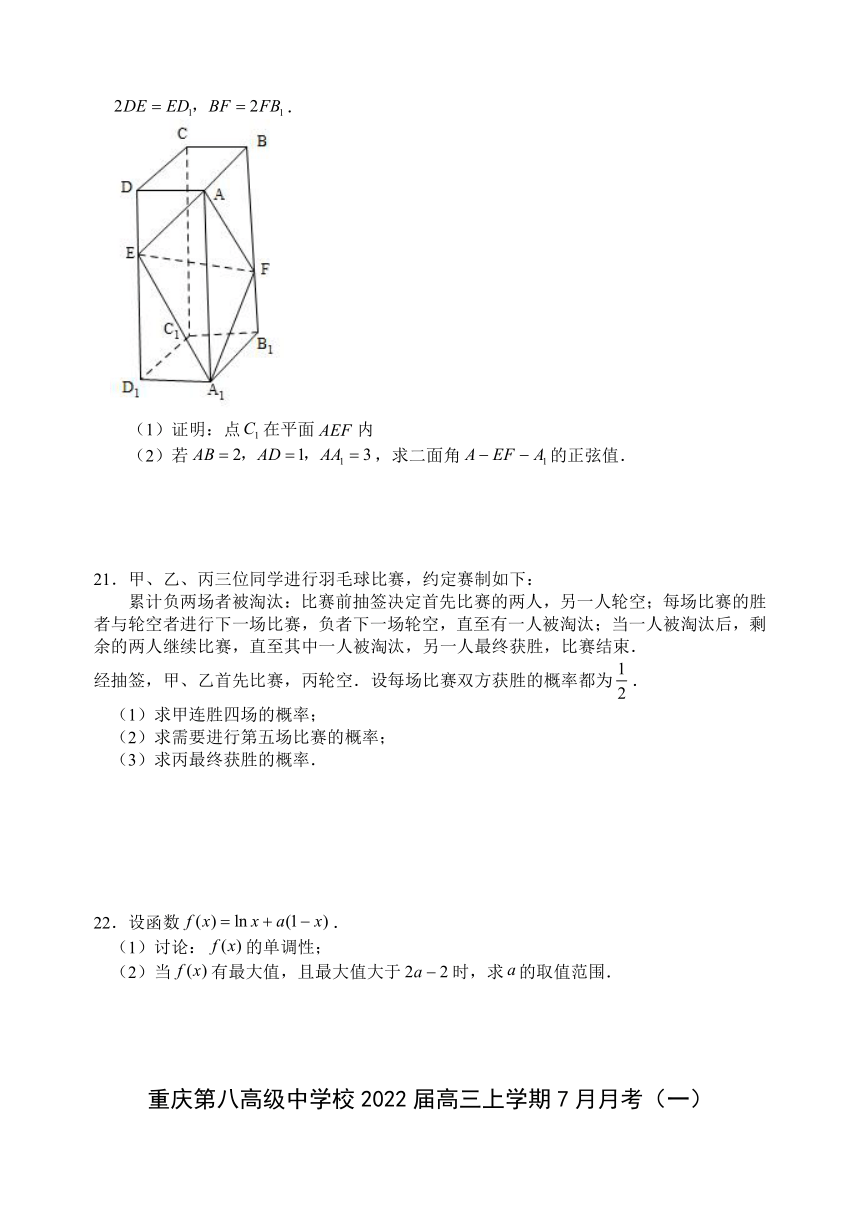
20.如图,在长方体false中,点false分别在棱false上,且false.
(1)证明:点false在平面false内
(2)若false,求二面角false的正弦值.
21.甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:
累计负两场者被淘汰:比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束.
经抽签,甲、乙首先比赛,丙轮空.设每场比赛双方获胜的概率都为false.
(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
(3)求丙最终获胜的概率.
22.设函数false.
(1)讨论:false的单调性;
(2)当false有最大值,且最大值大于false时,求false的取值范围.
重庆第八高级中学校2022届高三上学期7月月考(一)
数学答案(艺术班)
选择题:本题共8小题,每小题5分,共40分。在每小题列出的的四个选项中,只有一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
答案
A
A
B
B
C
B
B
D
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
题号
9
10
11
12
答案
ABD
BC
AC
AC
三、填空题:本题共4小题,每小题5分,共20分。
13.15; 14.0或3; 15.0.6 ; 16.false,false.
四.解答题:本题共6小题,共70分. 解答应写出必要文字说明、证明过程或演算步骤。
17.【答案】解:(1)由,,
则
解得:或
由于数列为递增数列,
则:,.
故:,
则:.
(2)由于,
则:
.
所以:.
18.【答案】解:(1)数学成绩的茎叶图如图:
(2)该样本的中位数为86,众数为82.
(3)样本中“及格”的学生人数为10,其中成绩在区间的有4人,其余有6人,
所以X的所有可能取值为0,1,2,3.
,,
,.
X的分布列为
X
0
1
2
3
P
.
19.【答案】解:(1)因为中,内角A,B,C所对的边分别为a,b,c,.
所以,
故,
由于,
可得,解得.
(2)由余弦定理,可得:,
即,当且仅当时取等号;
所以的面积.
即的面积的最大值为.
20.【答案】解:(1)取线段上一点Q,使得,连接?,QD,FQ,
因为,
所以容易证明,,
所以四边形是平行四边形,
所以,
同理可以证明四边形DAFQ是平行四边形,
所以,
所以,
所以点,A,E,F四点共面,
即点在平面AEF内
(2)以为坐标原点,为x轴,为y轴,为z轴建立空间直角坐标系,
则1,,0,,1,,,
,,,
设平面AEF的法向量为y,,
则
令,可得,,则1,,
设平面的法向量为b,,
则
令,可得,,则4,
所以,
二面角的正弦值为.
【答案】(1)甲连胜四场只能是前四场全胜,.
(2)根据赛制,至少需要进行四场比赛,至多需要进行5场比赛,
比赛四场结束,共有三种情况:
甲连胜4场的概率为;
乙连胜4场的概率为;
丙上场后连胜3场的概率为;
所以需要进行第5场比赛的概率为,
丙最终获胜有两种情况:
比赛四场结束且丙最终获胜的概率为,
比赛五场结束且丙最终获胜,则从第二场开始的四场比赛按照丙的胜,负,轮空结果有3种情况:胜胜负胜,胜负空胜,负空胜胜,概率分别为,
因此丙最终获胜的概率为.
22.【答案】解:(1)的定义域为,
,
若,则,函数在上单调递增,
若,则当时,,
当时,,
所以在上单调递增,在上单调递减,
(2)由(1)知,当时,在上无最大值;当时,在取得最大值,
最大值为,
,
,
令,
在单调递增,,当时,,当时,,
的取值范围为.
数学试题(艺术班)
选择题:本题共8小题,每小题5分,共40分。在每小题列出的的四个选项中,只有一项是符合题目要求的。
1.设集合false,false,则false=( )
A.false B.false C.false D.false
2.复数false的共轭复数是( )
A.false B.false C.false D.false
3.若圆台下底半径为false,上底半径为false,母线长为false,则其体积为( )
A.false B.false C.false D.false
4.设函数false,下列结论中正确的是( )
A.false的最大值等于false
B.false的图象关于直线false对称
C.false在区间false上单调递增
D.false的图象关于点false对称
5.已知直线false过点false,且在两坐标轴上的截距互为相反数,则直线false的方程为( )
A.false B.false或false
C.false或false D.false或false
6.已知false,则false( )
A.false B.false C.false D.false
7.一组样本容量为false的样本数据构成一个公差不为false的等差数列false,若false,且false成等比数列,则此样本数据的平均数和中位数分别是( )
A.false B.false C.false D.false
8.若直线false与曲线false和圆false都相切,则false的方程为( )
A.false B.false C.false D.false
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
9.某中学高一年级有false个班,每班false人;高二年级有false个班,每班false人甲就读于高一,乙就读于高二学校计划从这两个年级中共抽取false人进行视力调查,下列说法中正确的有( )
A.应该采用分层随机抽样法
B.高一、高二年级应分别抽取false人和false人
C.乙被抽到的可能性比甲大
D.该问题中的总体是高一、高二年级的全体学生的视力
10.已知向量false,则( )
A.若false与false垂直,则false
B.若false,则false的值为
C.若false,则false
D.若false,则false与false的夹角为false
11.已知false是两条不同的直线,false是两个不同的平面,有下列命题正确的是( )
A.若false,则false
B.若false,则false
C.若false,则false
D.若false,则false
12.已知圆false,直线false,则下列正确的是( )
A.直线false恒过定点false
B.当false时,圆false上有且仅有三个点到直线false的距离都等于1
C.圆false与曲线false恰有三条公切线,则false
D.当false时,直线false上一个动点false向圆false引两条切线false,其中false为切点,则直线false经过点 false
三、填空题:本题共4小题,每小题5分,共20分。
13.已知false是等差数列,若false,则false____________;
14.若两条直线false和false互相垂直,则false的值为____________;
15.某群体中的每位成员使用移动支付的概率都为false,各成员的支付方式相互独立.设false为该群体的10位成员中使用移动支付的人数,false,则false____________;
16.函数false的单调减区间为____________;若函数false在false上在取得最小值false,则实数a的取值范围是____________.
四.解答题:本题共6小题,共70分. 解答应写出必要文字说明、证明过程或演算步骤。
17.已知等差数列false是递增数列,且false.
(1)求数列false的通项公式;
(2)若false,求数列false的前false项和false.
18.某校为了解“准高三”学生的数学成绩情况,从一次模拟考试中随机抽取了false名学生的数学成绩如下:
78? 64 ? 88? 104? 53? 82? 86? 93? 90? 105? 77? 92? 116
81? 60? 82? 74? 105? 91? 103? 78 88 107? 82? 71
(1)完成这false名学生的数学成绩的茎叶图如图;
(2)确定该样本的中位数和众数;
(3)规定数学成绩不低于false分为“及格”,从该样本“及格”的学生中任意抽出false名,设抽到成绩在区间false的学生人数为false,求false的分布列和数学期望false.
19.在false中,内角false所对的边分别为false,已知false.
(1)求角false的大小;
(2)若false,求false的面积的最大值.
20.如图,在长方体false中,点false分别在棱false上,且false.
(1)证明:点false在平面false内
(2)若false,求二面角false的正弦值.
21.甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:
累计负两场者被淘汰:比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束.
经抽签,甲、乙首先比赛,丙轮空.设每场比赛双方获胜的概率都为false.
(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
(3)求丙最终获胜的概率.
22.设函数false.
(1)讨论:false的单调性;
(2)当false有最大值,且最大值大于false时,求false的取值范围.
重庆第八高级中学校2022届高三上学期7月月考(一)
数学答案(艺术班)
选择题:本题共8小题,每小题5分,共40分。在每小题列出的的四个选项中,只有一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
答案
A
A
B
B
C
B
B
D
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
题号
9
10
11
12
答案
ABD
BC
AC
AC
三、填空题:本题共4小题,每小题5分,共20分。
13.15; 14.0或3; 15.0.6 ; 16.false,false.
四.解答题:本题共6小题,共70分. 解答应写出必要文字说明、证明过程或演算步骤。
17.【答案】解:(1)由,,
则
解得:或
由于数列为递增数列,
则:,.
故:,
则:.
(2)由于,
则:
.
所以:.
18.【答案】解:(1)数学成绩的茎叶图如图:
(2)该样本的中位数为86,众数为82.
(3)样本中“及格”的学生人数为10,其中成绩在区间的有4人,其余有6人,
所以X的所有可能取值为0,1,2,3.
,,
,.
X的分布列为
X
0
1
2
3
P
.
19.【答案】解:(1)因为中,内角A,B,C所对的边分别为a,b,c,.
所以,
故,
由于,
可得,解得.
(2)由余弦定理,可得:,
即,当且仅当时取等号;
所以的面积.
即的面积的最大值为.
20.【答案】解:(1)取线段上一点Q,使得,连接?,QD,FQ,
因为,
所以容易证明,,
所以四边形是平行四边形,
所以,
同理可以证明四边形DAFQ是平行四边形,
所以,
所以,
所以点,A,E,F四点共面,
即点在平面AEF内
(2)以为坐标原点,为x轴,为y轴,为z轴建立空间直角坐标系,
则1,,0,,1,,,
,,,
设平面AEF的法向量为y,,
则
令,可得,,则1,,
设平面的法向量为b,,
则
令,可得,,则4,
所以,
二面角的正弦值为.
【答案】(1)甲连胜四场只能是前四场全胜,.
(2)根据赛制,至少需要进行四场比赛,至多需要进行5场比赛,
比赛四场结束,共有三种情况:
甲连胜4场的概率为;
乙连胜4场的概率为;
丙上场后连胜3场的概率为;
所以需要进行第5场比赛的概率为,
丙最终获胜有两种情况:
比赛四场结束且丙最终获胜的概率为,
比赛五场结束且丙最终获胜,则从第二场开始的四场比赛按照丙的胜,负,轮空结果有3种情况:胜胜负胜,胜负空胜,负空胜胜,概率分别为,
因此丙最终获胜的概率为.
22.【答案】解:(1)的定义域为,
,
若,则,函数在上单调递增,
若,则当时,,
当时,,
所以在上单调递增,在上单调递减,
(2)由(1)知,当时,在上无最大值;当时,在取得最大值,
最大值为,
,
,
令,
在单调递增,,当时,,当时,,
的取值范围为.
同课章节目录
