4.3.3余角和补角-- 课堂过关试卷 2021--2022学年人教版数学七年级上册(Word版含答案)
文档属性
| 名称 | 4.3.3余角和补角-- 课堂过关试卷 2021--2022学年人教版数学七年级上册(Word版含答案) | 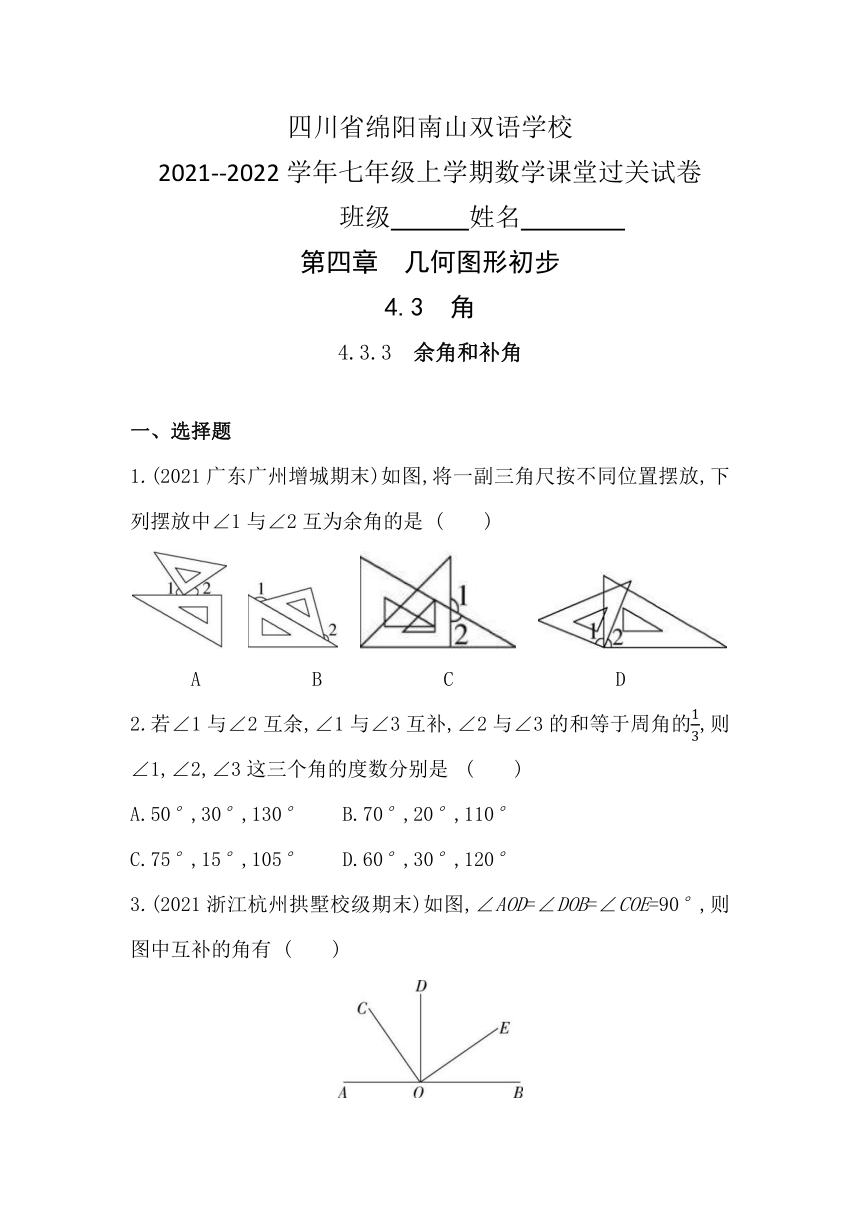 | |
| 格式 | docx | ||
| 文件大小 | 122.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 15:20:18 | ||
图片预览



文档简介
四川省绵阳南山双语学校
2021--2022学年七年级上学期数学课堂过关试卷
班级
姓名
第四章 几何图形初步
4.3 角
4.3.3 余角和补角
一、选择题
1.(2021广东广州增城期末)如图,将一副三角尺按不同位置摆放,下列摆放中∠1与∠2互为余角的是
( )
A
B
C
D
2.若∠1与∠2互余,∠1与∠3互补,∠2与∠3的和等于周角的,则∠1,∠2,∠3这三个角的度数分别是
( )
A.50°,30°,130°
B.70°,20°,110°
C.75°,15°,105°
D.60°,30°,120°
3.(2021浙江杭州拱墅校级期末)如图,∠AOD=∠DOB=∠COE=90°,则图中互补的角有
( )
A.5对
B.6对
C.7对
D.8对
4.如图,将一个含60°角的三角板的60°角的顶点与另一个三角板的直角顶点重合,若∠1=27°41',则∠2的余角的大小是
( )
A.27°41'
B.57°41'
C.58°19'
D.32°19'
5.(2021甘肃定西安定期末)一个角的余角是它的补角的,则这个角的度数为
( )
A.60°
B.45°
C.30°
D.75°
6.(2021辽宁葫芦岛绥中期末)下列说法正确的是
( )
A.锐角的补角一定是钝角
B.一个角的补角一定大于这个角
C.锐角和钝角一定互补
D.两个锐角一定互为余角
7.如图,甲从A点出发沿北偏东60°方向走到点B,乙从点A出发沿南偏西20°方向走到点C,则∠BAC的度数是( )
A.80°
B.100°
C.120°
D.140°
8.(2021天津滨海新区期末)如图,∠AOD=120°,OC平分∠AOD,OB平分∠AOC.下列结论:
①∠AOC=∠COD;
②∠COD=2∠BOC;
③∠AOB与∠COD互余;
④∠AOC与∠AOD互补.
其中,正确的个数是
( )
A.1
B.2
C.3
D.4
二、填空题
9.如果一个角的余角与它的补角度数之比为2∶5,则这个角等于 .?
10.已知∠α与∠β互为余角,∠α=38°24',则∠β= .?
11.已知∠A和∠B互为余角,∠A=60°,则∠B的度数是 ,∠A的补角的度数是 .?
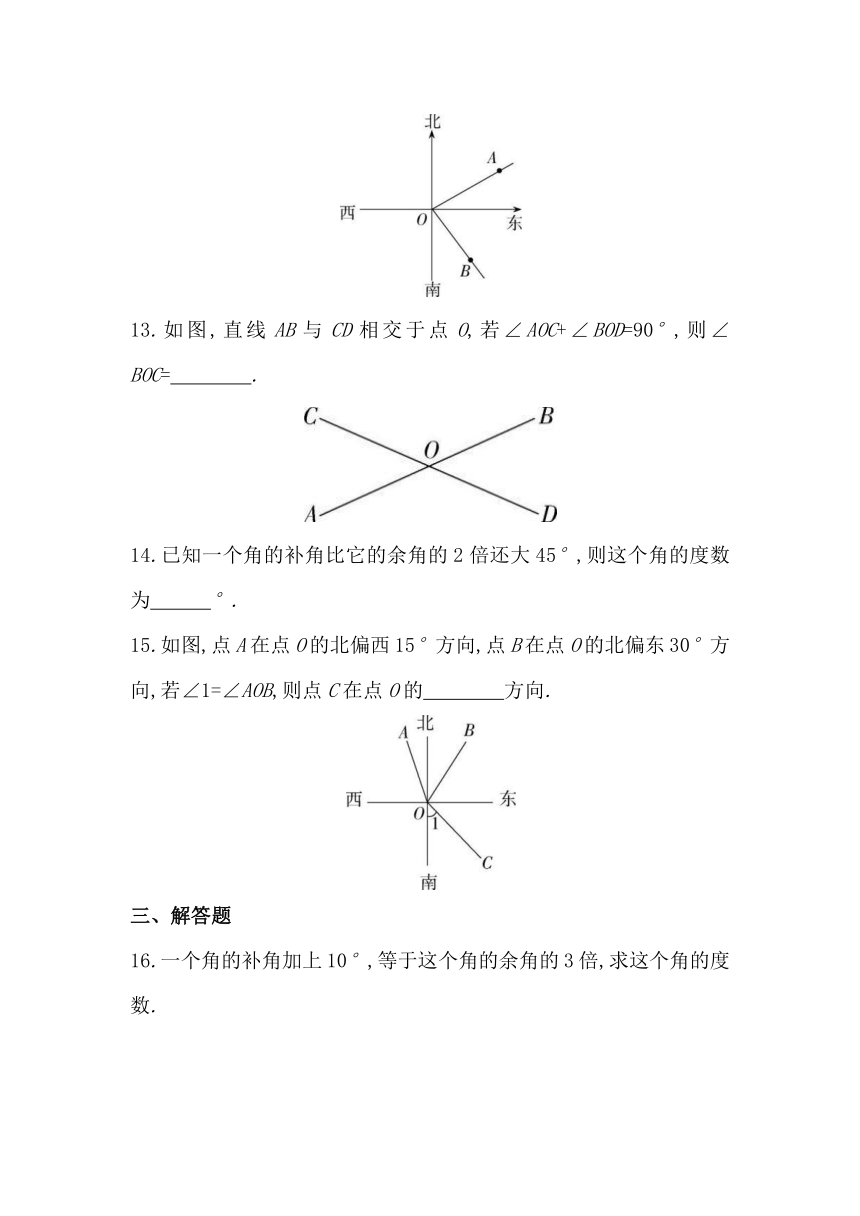
12.如图,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在它北偏东60°的方向上,观测到小岛B在它南偏东38°的方向上,则∠AOB的度数是 .?
13.如图,直线AB与CD相交于点O,若∠AOC+∠BOD=90°,则∠BOC= .?
14.已知一个角的补角比它的余角的2倍还大45°,则这个角的度数为 °.?
15.如图,点A在点O的北偏西15°方向,点B在点O的北偏东30°方向,若∠1=∠AOB,则点C在点O的 方向.?
三、解答题
16.一个角的补角加上10°,等于这个角的余角的3倍,求这个角的度数.
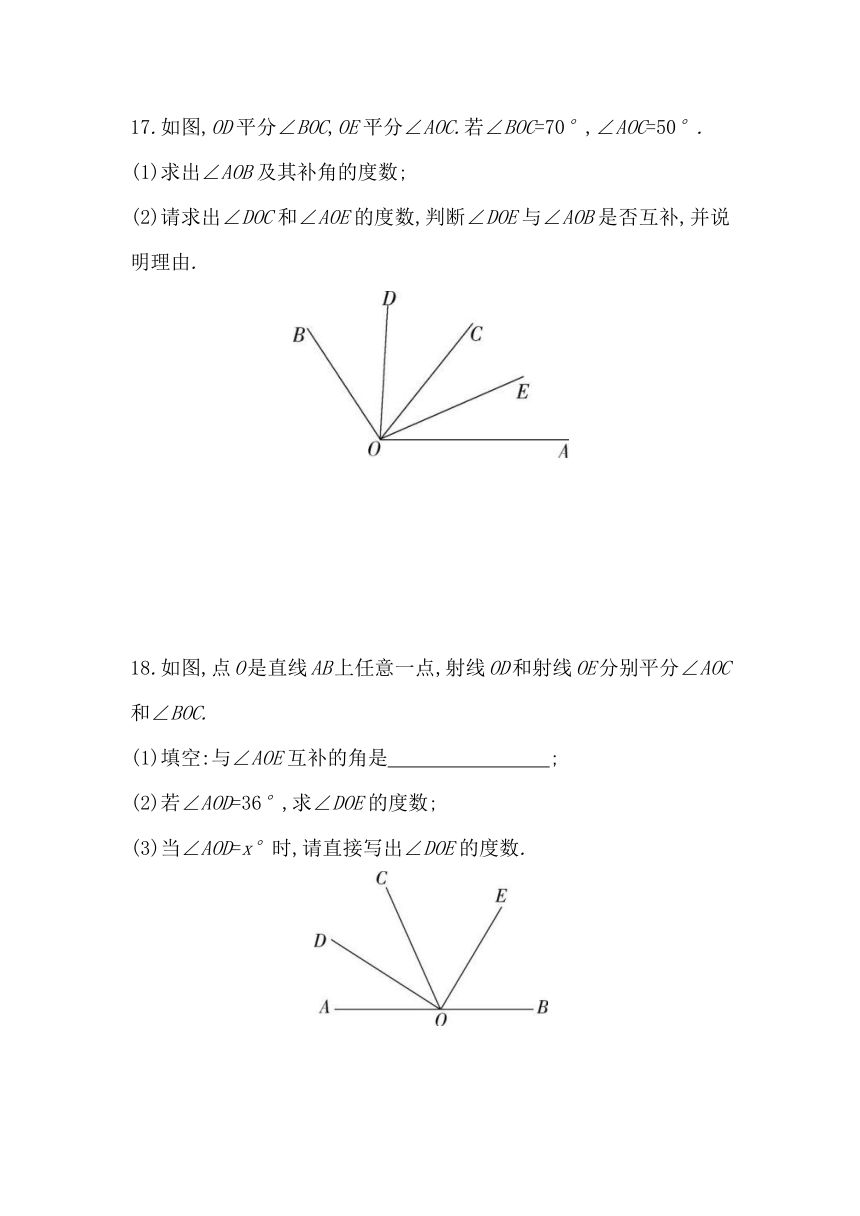
17.如图,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,判断∠DOE与∠AOB是否互补,并说明理由.
18.如图,点O是直线AB上任意一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠AOE互补的角是 ;?
(2)若∠AOD=36°,求∠DOE的度数;
(3)当∠AOD=x°时,请直接写出∠DOE的度数.
19.如图,OA的方向是北偏东15°,OB的方向是西偏北50°.
(1)若∠AOC=∠AOB,求OC的方向;
(2)OD是OB的反向延长线,求OD的方向;
(3)∠BOD可看作是OB绕点O顺时针方向旋转至OD,作∠BOD的平分线OE,求OE的方向.
20.我们规定,如果两个角的差是一个直角(大角减小角),那么这两个角互为足角,其中的一个角叫做另一个角的足角.
(1)如图,直线AB经过点O,OE平分∠COB,OF⊥OE.请直接写出图中∠BOF的足角;
(2)如果一个角的足角等于这个角的补角的,求这个角的度数.
21.(1)如图1所示,一副直角三角尺的直角顶点重合在点O处.
①∠AOC与∠BOD相等吗?说明理由;
②∠AOD与∠BOC数量上有什么关系?说明理由;
(2)若将这副直角三角尺按图2所示的方式摆放,直角顶点重合在点O处,不添加字母,分析图中已标注字母所表示的角.
①找出图中相等的角;
②找出图中互补的角,并说明理由.
一、选择题
1.答案 A A.∠1+∠2=90°,即∠1与∠2互为余角,故正确;
B.∠1=∠2,故错误;
C.∠1+∠2=180°,即∠1与∠2互为补角,故错误;
D.∠1=∠2,故错误.
故选A.
2.答案 C 设∠1=x°,则∠2=(90-x)°,∠3=(180-x)°,
易知∠2+∠3=120°,所以90-x+180-x=120,
所以x=75,所以∠1=75°,∠2=15°,∠3=105°.故选C.
3.答案 C 互补的角有:∠AOD与∠BOD,∠AOD与∠COE,∠COE与∠BOD,∠AOC与∠BOC,∠DOE与∠BOC,∠AOE与∠BOE,∠AOE与∠COD,共7对,故选C.
4.答案 D 因为∠BAC=60°,∠1=27°41',
所以∠EAC=32°19',
因为∠EAD=90°,
所以∠2与∠EAC互余,
所以∠2的余角的大小为32°19'.故选D.
5.答案 C 设这个角的度数是x°,则90-x=(180-x),
解得x=30,即这个角的度数是30°,故选C.
6.答案 A 锐角的补角一定是钝角,选项A正确;
一个角的补角不一定大于这个角,B选项说法错误,例如:120°角的补角是60°的角,而60°<120°;
锐角和钝角不一定互补,C选项说法错误,例如:20°+120°=140°,20°的角与120°的角不互补;
两个锐角不一定互为余角,D选项说法错误,例如:30°的角与30°的角不是互为余角.故选A.
7.答案 D 如图,因为∠DAB=60°,所以∠BAF=30°,
因为∠CAE=20°,所以∠BAC=∠CAE+∠EAF+∠BAF=20°+90°+30°=140°,故选D.
8.答案 D ①因为OC平分∠AOD,所以∠AOC=∠COD=∠AOD=60°,故①正确.
②因为OB平分∠AOC,所以∠AOC=2∠BOC,所以∠COD=2∠BOC,故②正确.
③因为∠AOB=∠BOC=∠AOC=30°,所以∠AOB+∠COD=90°,所以∠AOB与∠COD互余,故③正确.
④因为∠AOC+∠AOD=60°+120°=180°,所以∠AOC与∠AOD互补,故④正确.
故选D.
二、填空题
9.答案 30°
解析 设该角的度数为x°,则它的余角的度数为(90-x)°,补角的度数为(180-x)°,
根据题意得(90-x)∶(180-x)=2∶5,解得x=30.
所以这个角等于30°.
10.答案 51°36'(或51.6°)
解析 因为∠α与∠β互为余角,∠α=38°24',
所以∠β=90°-38°24'=51°36'(或51.6°).
11.答案 30°;120°
解析 因为∠A和∠B互为余角,∠A=60°,
所以∠B=90°-∠A=90°-60°=30°.
∠A的补角=180°-∠A=180°-60°=120°.
12.答案 82°
解析 由已知得,∠AOB=180°-60°-38°=82°.
13.答案 135°
解析 因为∠AOC和∠BOD都是∠BOC的补角,
所以∠AOC=∠BOD,
又因为∠AOC+∠BOD=90°,
所以∠AOC=∠BOD=45°,
所以∠BOC=135°.
14.答案 45
解析 设这个角的度数为x,则它的余角的度数为90°-x,补角的度数为180°-x,
根据题意得180°-x=2(90°-x)+45°,
解得x=45°,
所以这个角的度数为45°.
15.答案 东南
解析 由题意知,∠AOB=15°+30°=45°.
因为∠1=∠AOB,所以∠1=45°.
所以点C在点O的东南方向.
三、解答题
16.解析 设这个角的度数为x°,则它的补角的度数为(180-x)°,它的余角的度数为(90-x)°,
根据题意,得(180-x)+10=3(90-x),解得x=40.
所以这个角的度数为40°.
17.解析 (1)∠AOB=∠BOC+∠AOC=70°+50°=120°,
∠AOB的补角的度数为180°-∠AOB=180°-120°=60°.
(2)∠DOC=∠BOC=×70°=35°,
∠AOE=∠COE=∠AOC=×50°=25°.
∠DOE与∠AOB互补.
理由:因为∠DOE=∠DOC+∠COE=60°,
所以∠DOE+∠AOB=60°+120°=180°,
所以∠DOE与∠AOB互补.
18.解析 (1)因为OE平分∠BOC,所以∠BOE=∠COE.
因为∠AOE+∠BOE=180°,所以∠AOE+∠COE=180°,
所以与∠AOE互补的角是∠BOE、∠COE.
故答案为∠BOE、∠COE.
(2)因为OD、OE分别平分∠AOC、∠BOC,
所以∠COD=∠AOD=36°,∠COE=∠BOE=∠BOC,
所以∠AOC=2×36°=72°,
所以∠BOC=180°-72°=108°,
所以∠COE=∠BOC=54°,
所以∠DOE=∠COD+∠COE=90°.
(3)当∠AOD=x°时,∠DOE=90°.
19.解析 (1)如图,因为OB的方向是西偏北50°,
所以∠BOF=90°-50°=40°,
所以∠AOB=40°+15°=55°,
因为∠AOC=∠AOB,
所以∠AOC=55°,
所以∠FOC=∠AOF+∠AOC=15°+55°=70°,
所以OC的方向是北偏东70°.
(2)因为OB的方向是西偏北50°,
所以∠BOF=40°,
因为∠DOH和∠BOF都是∠BOH的补角,
所以∠DOH=∠BOF=40°,
所以OD的方向是南偏东40°.
(3)因为OE是∠BOD的平分线,
所以∠BOE=90°,
因为∠BOF=40°,
所以∠FOE=50°,
所以OE的方向是北偏东50°.
20.解析 (1)因为OE平分∠COB,
所以∠BOE=∠COE,
因为OF⊥OE,
所以∠BOF-∠BOE=90°,
所以∠BOF-∠COE=90°,
所以∠BOF的足角是∠COE、∠BOE.
(2)设这个角的度数为x°,则它的补角的度数为(180-x)°,
当0则有90+x=(180-x),
解得x=18;
当90则有x-90=(180-x).
解得x=126.
所以这个角的度数为18°或126°.
21.解析 (1)①∠AOC与∠BOD相等.
理由如下:因为∠AOB=∠DOC=90°,
所以∠AOB+∠BOC=∠DOC+∠BOC,
即∠AOC=∠BOD.
②∠AOD+∠BOC=180°.
理由如下:因为∠AOD+∠BOC+∠COD+∠AOB=360°,
∠AOB=∠COD=90°,
所以∠AOD+∠BOC=180°.
(2)①∠AOB=∠COD,∠AOC=∠BOD.
②∠AOB与∠COD互补,∠AOD与∠BOC互补.
理由如下:因为∠AOB=∠COD=90°,
所以∠AOB+∠COD=180°,即∠AOB与∠COD互补.
因为∠AOD=∠AOB+∠BOD=90°+∠BOD,
∠BOC=∠COD-∠BOD=90°-∠BOD,
所以∠AOD+∠BOC=90°+∠BOD+90°-∠BOD=180°,
所以∠AOD与∠BOC互补.
2021--2022学年七年级上学期数学课堂过关试卷
班级
姓名
第四章 几何图形初步
4.3 角
4.3.3 余角和补角
一、选择题
1.(2021广东广州增城期末)如图,将一副三角尺按不同位置摆放,下列摆放中∠1与∠2互为余角的是
( )
A
B
C
D
2.若∠1与∠2互余,∠1与∠3互补,∠2与∠3的和等于周角的,则∠1,∠2,∠3这三个角的度数分别是
( )
A.50°,30°,130°
B.70°,20°,110°
C.75°,15°,105°
D.60°,30°,120°
3.(2021浙江杭州拱墅校级期末)如图,∠AOD=∠DOB=∠COE=90°,则图中互补的角有
( )
A.5对
B.6对
C.7对
D.8对
4.如图,将一个含60°角的三角板的60°角的顶点与另一个三角板的直角顶点重合,若∠1=27°41',则∠2的余角的大小是
( )
A.27°41'
B.57°41'
C.58°19'
D.32°19'
5.(2021甘肃定西安定期末)一个角的余角是它的补角的,则这个角的度数为
( )
A.60°
B.45°
C.30°
D.75°
6.(2021辽宁葫芦岛绥中期末)下列说法正确的是
( )
A.锐角的补角一定是钝角
B.一个角的补角一定大于这个角
C.锐角和钝角一定互补
D.两个锐角一定互为余角
7.如图,甲从A点出发沿北偏东60°方向走到点B,乙从点A出发沿南偏西20°方向走到点C,则∠BAC的度数是( )
A.80°
B.100°
C.120°
D.140°
8.(2021天津滨海新区期末)如图,∠AOD=120°,OC平分∠AOD,OB平分∠AOC.下列结论:
①∠AOC=∠COD;
②∠COD=2∠BOC;
③∠AOB与∠COD互余;
④∠AOC与∠AOD互补.
其中,正确的个数是
( )
A.1
B.2
C.3
D.4
二、填空题
9.如果一个角的余角与它的补角度数之比为2∶5,则这个角等于 .?
10.已知∠α与∠β互为余角,∠α=38°24',则∠β= .?
11.已知∠A和∠B互为余角,∠A=60°,则∠B的度数是 ,∠A的补角的度数是 .?
12.如图,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在它北偏东60°的方向上,观测到小岛B在它南偏东38°的方向上,则∠AOB的度数是 .?
13.如图,直线AB与CD相交于点O,若∠AOC+∠BOD=90°,则∠BOC= .?
14.已知一个角的补角比它的余角的2倍还大45°,则这个角的度数为 °.?
15.如图,点A在点O的北偏西15°方向,点B在点O的北偏东30°方向,若∠1=∠AOB,则点C在点O的 方向.?
三、解答题
16.一个角的补角加上10°,等于这个角的余角的3倍,求这个角的度数.
17.如图,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,判断∠DOE与∠AOB是否互补,并说明理由.
18.如图,点O是直线AB上任意一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠AOE互补的角是 ;?
(2)若∠AOD=36°,求∠DOE的度数;
(3)当∠AOD=x°时,请直接写出∠DOE的度数.
19.如图,OA的方向是北偏东15°,OB的方向是西偏北50°.
(1)若∠AOC=∠AOB,求OC的方向;
(2)OD是OB的反向延长线,求OD的方向;
(3)∠BOD可看作是OB绕点O顺时针方向旋转至OD,作∠BOD的平分线OE,求OE的方向.
20.我们规定,如果两个角的差是一个直角(大角减小角),那么这两个角互为足角,其中的一个角叫做另一个角的足角.
(1)如图,直线AB经过点O,OE平分∠COB,OF⊥OE.请直接写出图中∠BOF的足角;
(2)如果一个角的足角等于这个角的补角的,求这个角的度数.
21.(1)如图1所示,一副直角三角尺的直角顶点重合在点O处.
①∠AOC与∠BOD相等吗?说明理由;
②∠AOD与∠BOC数量上有什么关系?说明理由;
(2)若将这副直角三角尺按图2所示的方式摆放,直角顶点重合在点O处,不添加字母,分析图中已标注字母所表示的角.
①找出图中相等的角;
②找出图中互补的角,并说明理由.
一、选择题
1.答案 A A.∠1+∠2=90°,即∠1与∠2互为余角,故正确;
B.∠1=∠2,故错误;
C.∠1+∠2=180°,即∠1与∠2互为补角,故错误;
D.∠1=∠2,故错误.
故选A.
2.答案 C 设∠1=x°,则∠2=(90-x)°,∠3=(180-x)°,
易知∠2+∠3=120°,所以90-x+180-x=120,
所以x=75,所以∠1=75°,∠2=15°,∠3=105°.故选C.
3.答案 C 互补的角有:∠AOD与∠BOD,∠AOD与∠COE,∠COE与∠BOD,∠AOC与∠BOC,∠DOE与∠BOC,∠AOE与∠BOE,∠AOE与∠COD,共7对,故选C.
4.答案 D 因为∠BAC=60°,∠1=27°41',
所以∠EAC=32°19',
因为∠EAD=90°,
所以∠2与∠EAC互余,
所以∠2的余角的大小为32°19'.故选D.
5.答案 C 设这个角的度数是x°,则90-x=(180-x),
解得x=30,即这个角的度数是30°,故选C.
6.答案 A 锐角的补角一定是钝角,选项A正确;
一个角的补角不一定大于这个角,B选项说法错误,例如:120°角的补角是60°的角,而60°<120°;
锐角和钝角不一定互补,C选项说法错误,例如:20°+120°=140°,20°的角与120°的角不互补;
两个锐角不一定互为余角,D选项说法错误,例如:30°的角与30°的角不是互为余角.故选A.
7.答案 D 如图,因为∠DAB=60°,所以∠BAF=30°,
因为∠CAE=20°,所以∠BAC=∠CAE+∠EAF+∠BAF=20°+90°+30°=140°,故选D.
8.答案 D ①因为OC平分∠AOD,所以∠AOC=∠COD=∠AOD=60°,故①正确.
②因为OB平分∠AOC,所以∠AOC=2∠BOC,所以∠COD=2∠BOC,故②正确.
③因为∠AOB=∠BOC=∠AOC=30°,所以∠AOB+∠COD=90°,所以∠AOB与∠COD互余,故③正确.
④因为∠AOC+∠AOD=60°+120°=180°,所以∠AOC与∠AOD互补,故④正确.
故选D.
二、填空题
9.答案 30°
解析 设该角的度数为x°,则它的余角的度数为(90-x)°,补角的度数为(180-x)°,
根据题意得(90-x)∶(180-x)=2∶5,解得x=30.
所以这个角等于30°.
10.答案 51°36'(或51.6°)
解析 因为∠α与∠β互为余角,∠α=38°24',
所以∠β=90°-38°24'=51°36'(或51.6°).
11.答案 30°;120°
解析 因为∠A和∠B互为余角,∠A=60°,
所以∠B=90°-∠A=90°-60°=30°.
∠A的补角=180°-∠A=180°-60°=120°.
12.答案 82°
解析 由已知得,∠AOB=180°-60°-38°=82°.
13.答案 135°
解析 因为∠AOC和∠BOD都是∠BOC的补角,
所以∠AOC=∠BOD,
又因为∠AOC+∠BOD=90°,
所以∠AOC=∠BOD=45°,
所以∠BOC=135°.
14.答案 45
解析 设这个角的度数为x,则它的余角的度数为90°-x,补角的度数为180°-x,
根据题意得180°-x=2(90°-x)+45°,
解得x=45°,
所以这个角的度数为45°.
15.答案 东南
解析 由题意知,∠AOB=15°+30°=45°.
因为∠1=∠AOB,所以∠1=45°.
所以点C在点O的东南方向.
三、解答题
16.解析 设这个角的度数为x°,则它的补角的度数为(180-x)°,它的余角的度数为(90-x)°,
根据题意,得(180-x)+10=3(90-x),解得x=40.
所以这个角的度数为40°.
17.解析 (1)∠AOB=∠BOC+∠AOC=70°+50°=120°,
∠AOB的补角的度数为180°-∠AOB=180°-120°=60°.
(2)∠DOC=∠BOC=×70°=35°,
∠AOE=∠COE=∠AOC=×50°=25°.
∠DOE与∠AOB互补.
理由:因为∠DOE=∠DOC+∠COE=60°,
所以∠DOE+∠AOB=60°+120°=180°,
所以∠DOE与∠AOB互补.
18.解析 (1)因为OE平分∠BOC,所以∠BOE=∠COE.
因为∠AOE+∠BOE=180°,所以∠AOE+∠COE=180°,
所以与∠AOE互补的角是∠BOE、∠COE.
故答案为∠BOE、∠COE.
(2)因为OD、OE分别平分∠AOC、∠BOC,
所以∠COD=∠AOD=36°,∠COE=∠BOE=∠BOC,
所以∠AOC=2×36°=72°,
所以∠BOC=180°-72°=108°,
所以∠COE=∠BOC=54°,
所以∠DOE=∠COD+∠COE=90°.
(3)当∠AOD=x°时,∠DOE=90°.
19.解析 (1)如图,因为OB的方向是西偏北50°,
所以∠BOF=90°-50°=40°,
所以∠AOB=40°+15°=55°,
因为∠AOC=∠AOB,
所以∠AOC=55°,
所以∠FOC=∠AOF+∠AOC=15°+55°=70°,
所以OC的方向是北偏东70°.
(2)因为OB的方向是西偏北50°,
所以∠BOF=40°,
因为∠DOH和∠BOF都是∠BOH的补角,
所以∠DOH=∠BOF=40°,
所以OD的方向是南偏东40°.
(3)因为OE是∠BOD的平分线,
所以∠BOE=90°,
因为∠BOF=40°,
所以∠FOE=50°,
所以OE的方向是北偏东50°.
20.解析 (1)因为OE平分∠COB,
所以∠BOE=∠COE,
因为OF⊥OE,
所以∠BOF-∠BOE=90°,
所以∠BOF-∠COE=90°,
所以∠BOF的足角是∠COE、∠BOE.
(2)设这个角的度数为x°,则它的补角的度数为(180-x)°,
当0
解得x=18;
当90
解得x=126.
所以这个角的度数为18°或126°.
21.解析 (1)①∠AOC与∠BOD相等.
理由如下:因为∠AOB=∠DOC=90°,
所以∠AOB+∠BOC=∠DOC+∠BOC,
即∠AOC=∠BOD.
②∠AOD+∠BOC=180°.
理由如下:因为∠AOD+∠BOC+∠COD+∠AOB=360°,
∠AOB=∠COD=90°,
所以∠AOD+∠BOC=180°.
(2)①∠AOB=∠COD,∠AOC=∠BOD.
②∠AOB与∠COD互补,∠AOD与∠BOC互补.
理由如下:因为∠AOB=∠COD=90°,
所以∠AOB+∠COD=180°,即∠AOB与∠COD互补.
因为∠AOD=∠AOB+∠BOD=90°+∠BOD,
∠BOC=∠COD-∠BOD=90°-∠BOD,
所以∠AOD+∠BOC=90°+∠BOD+90°-∠BOD=180°,
所以∠AOD与∠BOC互补.
