10.3.1频率的稳定性(18张PPT)
文档属性
| 名称 | 10.3.1频率的稳定性(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
人教A版(2019)
必修二
7.1复数的概念
10.3
频率与概率
10.3.1
频率的稳定性
对于样本点等可能的试验,我们可以用古典概型公式计算有关事件的概率.但在现实中,很多试验的样本点往往不是等可能的或者是否等可能不容易判断.例如,抛掷一枚质地不均匀的骰子,或者抛掷一枚图钉,此时无法通过古典概型公式计算有关事件的概率,我们需要寻找新的求概率的方法.
我们知道,事件的概率越大,意味着事件发生的可能性越大,在重复试验中,相应的频率一般也越大;事件的概率越小,则事件发生的可能性越小,在重复试验中,相应的频率一般也越小.在初中,我们利用频率与概率的这种关系,通过大量重复试验,用频率去估计概率.那么,在重复试验中,频率的大小是否就决定了概率的大小呢?频率与概率之间到底是一种怎样的关系呢?
探究
重复做同时抛掷两枚质地均匀的硬币的试验,设事件A
=
“一个正面朝上,一个反面朝上”,统计A出现的次数并计算频率,再与其概率进行比较.你发现了什么规律?
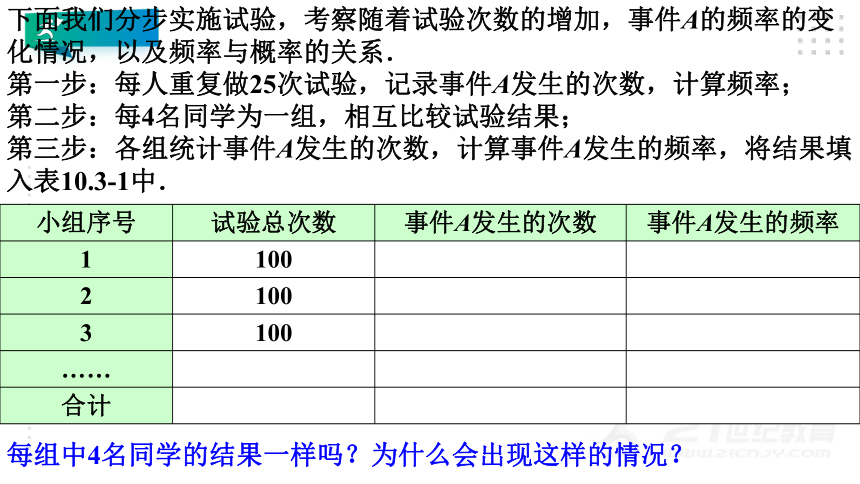
下面我们分步实施试验,考察随着试验次数的增加,事件A的频率的变化情况,以及频率与概率的关系.
第一步:每人重复做25次试验,记录事件A发生的次数,计算频率;
第二步:每4名同学为一组,相互比较试验结果;
第三步:各组统计事件A发生的次数,计算事件A发生的频率,将结果填入表10.3-1中.
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
100
2
100
3
100
……
合计
每组中4名同学的结果一样吗?为什么会出现这样的情况?
思考
比较在自己试验25次、小组试验100次和全班试验总次数的情况下,事件A发生的频率.
(1)各小组的试验结果一样吗?为什么会出现这种情况?
(2)随着试验次数的增加,事件A发生的频率有什么变化规律?
序号
n=20
n=100
n=500
频数
频率
频数
频率
频数
频率
1
12
0.6
56
0.56
261
0.522
2
9
0.45
50
0.50
241
0.482
3
13
0.65
48
0.48
250
0.5
4
7
0.35
55
0.55
258
0.516
5
12
0.6
52
0.52
253
0.506
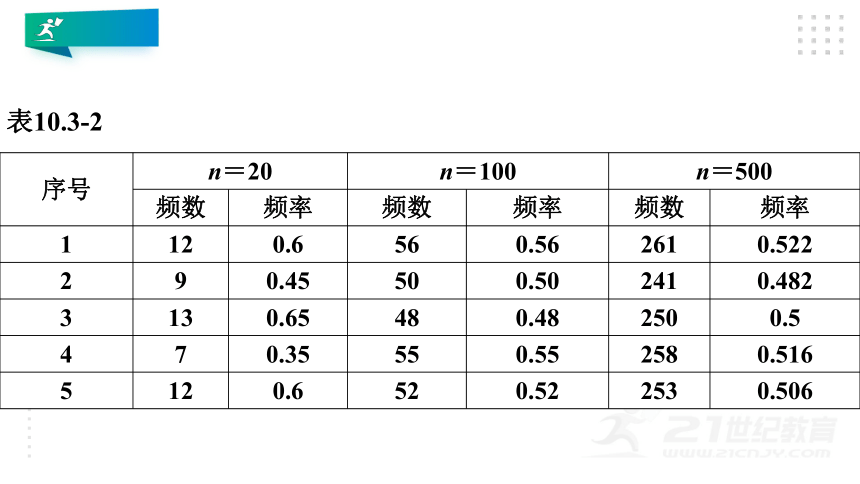
表10.3-2
用折线图表示频率的波动情况(图10.3-1).
从整体来看,频率在概率0.5附近波动.当试验次数较少时,波动幅度较大;当试验次数较大时,波动幅度较小.但试验次数多的波动幅度并不全都比次数少的小,只是波动幅度小的可能性更大.
雅各布第一
?伯努利(Jakob
I
Bernoulli,1654—1705)瑞士数学家,被公认为概率理论的先驱,他给出了著名的大数定律.大数定律阐述了随着试验次数的增加,频率稳定在概率附近.
例1
新生婴儿性别比是每100名女婴对应的男婴数.通过抽样调查得知,我国2014年、2015年出生的婴儿性别比分别为115.88和113.51.
分别估计我国2014年和2015年男婴的出生率(新生儿中男婴的比率,精确到0.001);
根据估计结果,你认为“生男孩和生女孩是等可能的”这个判断可靠吗?
由此估计,我国2014年男婴出生率约为0.537,2015年男婴出生率约为0.532.
(2)由于调查新生儿人数的样本非常大,根据频率的稳定性,上述对男婴出生率的估计具有较高的可信度.因此,我们有理由怀疑“生男孩和生女孩是等可能的”的结论.
例2
一个游戏包含两个随机事件A和B,规定事件A发生则甲获胜,事件B发生则乙获胜.判断游戏是否公平的标准是事件A和B发生的概率是否相等.
在游戏过程中甲发现:玩了10次时,双方各胜5次;但玩到1000次时,自己才胜300次,而乙却胜了700次.据此,甲认为游戏不公平,但乙认为游戏是公平的.你更支持谁的结论?为什么?
解:当游戏玩了10次时,甲、乙获胜的频率都为0.5;当游戏玩1000次时,甲获胜的频率为0.3,乙获胜的频率为0.7.根据频率的稳定性,随着试验次数的增加,频率偏离概率很大的可能性会越来越小.相对10次游戏,1000次游戏时的频率接近概率的可能性更大,因此我们更愿意相信1000次时的频率离概率更近.而游戏玩到1000次时,甲、乙获胜的频率分别是0.3和0.7,存在很大差距,所以有理由认为游戏是不公平的.因此,应该支持甲对游戏公平性的判断.
思考
气象工作者有时用概率预报天气,如某气象台预报“明天的降水概率是90%.如果您明天要出门,最好携带雨具”如果第二天没有下雨,我们或许会抱怨气象台预报得不准确.那么如何理解“降水概率是90%”?又该如何评价预报的结果是否准确呢?
降水的概率是气象专家根据气象条件和经验,经分析推断得到的.对“降水的概率为90%”比较合理的解释是:大量观察发现,在类似的气象条件下,大约有90%的天数要下雨.
只有根据气象预报的长期记录,才能评价预报的准确性.如果在类似气象条件下预报要下雨的那些天(天数较多)里,大约有90%确实下雨了,那么应该认为预报是准确的;如果真实下雨的天数所占的比例与90%差别较大,那么就可以认为预报不太准确.
练习(第254页)
1.判断下列说法是否正确,并说明理由:
(1)抛掷一枚硬币正面朝上的概率为0.5,则抛掷两枚硬币,一定是一次正面朝上,一次反面朝上;
(2)抛掷一枚质地均匀的硬币10次,结果是4次正面朝上,所以事件“正面朝上”的概率为0.4;
(3)当试验次数很大时,随机事件发生的频率接近其概率;
(4)在一次试验中,随机事件可能发生也可能不发生,所以事件发生和不发生的概率各是0.5.
(1)不正确.抛掷两枚硬币,“一次正面朝上,一次反面朝上”的概率是0.5,不是必然事件.
概率与频率有本质的区别.
(2)不正确.只能说频率是0.4,正面朝上的概率为
0.5.由于试验次数较少,频率与概率差别较大.
(3)正确.试验次数较大时,频率稳定到概率.
(4)不正确.随机事件发生的概率有大小之分.这种错误是
“等可能性偏见”.
2.用掷两枚硬币做胜负游戏,规定:两枚硬币同时出现正面或同时出现反面算甲胜,一个正面、一个反面算乙胜.这个游戏公平吗?
抛掷两枚质地均匀的硬币,同时出现正面或同时出现反面的概率为0.5,出现一个正面、一个反面的概率也为0.5,这个游戏是公平的.
3.据统计ABO血型具有民族和地区差异.在我国H省调査了30488人,四种血型的人数如下:
血型
A
B
O
AB
人数/人
7704
10765
8970
3049
频率
(1)计算H省各种血型的频率并填表(精确到0.001);
(2)如果从H省任意调查一个人的血型,那么他是O型血的概率大约是多少?
0.253
0.353
0.294
0.100
(2)他是O型血的概率大约是0.294
4.分别举出一个生活中概率很小和很大的例子.
例如,飞机失事是一个小概率事件,买福利彩票双色球中一等奖是小概率事件,购买一台知名品牌笔记本电脑,该电脑是合格品是一个概率很大的事件.
人教A版(2019)
必修二
7.1复数的概念
10.3
频率与概率
10.3.1
频率的稳定性
对于样本点等可能的试验,我们可以用古典概型公式计算有关事件的概率.但在现实中,很多试验的样本点往往不是等可能的或者是否等可能不容易判断.例如,抛掷一枚质地不均匀的骰子,或者抛掷一枚图钉,此时无法通过古典概型公式计算有关事件的概率,我们需要寻找新的求概率的方法.
我们知道,事件的概率越大,意味着事件发生的可能性越大,在重复试验中,相应的频率一般也越大;事件的概率越小,则事件发生的可能性越小,在重复试验中,相应的频率一般也越小.在初中,我们利用频率与概率的这种关系,通过大量重复试验,用频率去估计概率.那么,在重复试验中,频率的大小是否就决定了概率的大小呢?频率与概率之间到底是一种怎样的关系呢?
探究
重复做同时抛掷两枚质地均匀的硬币的试验,设事件A
=
“一个正面朝上,一个反面朝上”,统计A出现的次数并计算频率,再与其概率进行比较.你发现了什么规律?
下面我们分步实施试验,考察随着试验次数的增加,事件A的频率的变化情况,以及频率与概率的关系.
第一步:每人重复做25次试验,记录事件A发生的次数,计算频率;
第二步:每4名同学为一组,相互比较试验结果;
第三步:各组统计事件A发生的次数,计算事件A发生的频率,将结果填入表10.3-1中.
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
100
2
100
3
100
……
合计
每组中4名同学的结果一样吗?为什么会出现这样的情况?
思考
比较在自己试验25次、小组试验100次和全班试验总次数的情况下,事件A发生的频率.
(1)各小组的试验结果一样吗?为什么会出现这种情况?
(2)随着试验次数的增加,事件A发生的频率有什么变化规律?
序号
n=20
n=100
n=500
频数
频率
频数
频率
频数
频率
1
12
0.6
56
0.56
261
0.522
2
9
0.45
50
0.50
241
0.482
3
13
0.65
48
0.48
250
0.5
4
7
0.35
55
0.55
258
0.516
5
12
0.6
52
0.52
253
0.506
表10.3-2
用折线图表示频率的波动情况(图10.3-1).
从整体来看,频率在概率0.5附近波动.当试验次数较少时,波动幅度较大;当试验次数较大时,波动幅度较小.但试验次数多的波动幅度并不全都比次数少的小,只是波动幅度小的可能性更大.
雅各布第一
?伯努利(Jakob
I
Bernoulli,1654—1705)瑞士数学家,被公认为概率理论的先驱,他给出了著名的大数定律.大数定律阐述了随着试验次数的增加,频率稳定在概率附近.
例1
新生婴儿性别比是每100名女婴对应的男婴数.通过抽样调查得知,我国2014年、2015年出生的婴儿性别比分别为115.88和113.51.
分别估计我国2014年和2015年男婴的出生率(新生儿中男婴的比率,精确到0.001);
根据估计结果,你认为“生男孩和生女孩是等可能的”这个判断可靠吗?
由此估计,我国2014年男婴出生率约为0.537,2015年男婴出生率约为0.532.
(2)由于调查新生儿人数的样本非常大,根据频率的稳定性,上述对男婴出生率的估计具有较高的可信度.因此,我们有理由怀疑“生男孩和生女孩是等可能的”的结论.
例2
一个游戏包含两个随机事件A和B,规定事件A发生则甲获胜,事件B发生则乙获胜.判断游戏是否公平的标准是事件A和B发生的概率是否相等.
在游戏过程中甲发现:玩了10次时,双方各胜5次;但玩到1000次时,自己才胜300次,而乙却胜了700次.据此,甲认为游戏不公平,但乙认为游戏是公平的.你更支持谁的结论?为什么?
解:当游戏玩了10次时,甲、乙获胜的频率都为0.5;当游戏玩1000次时,甲获胜的频率为0.3,乙获胜的频率为0.7.根据频率的稳定性,随着试验次数的增加,频率偏离概率很大的可能性会越来越小.相对10次游戏,1000次游戏时的频率接近概率的可能性更大,因此我们更愿意相信1000次时的频率离概率更近.而游戏玩到1000次时,甲、乙获胜的频率分别是0.3和0.7,存在很大差距,所以有理由认为游戏是不公平的.因此,应该支持甲对游戏公平性的判断.
思考
气象工作者有时用概率预报天气,如某气象台预报“明天的降水概率是90%.如果您明天要出门,最好携带雨具”如果第二天没有下雨,我们或许会抱怨气象台预报得不准确.那么如何理解“降水概率是90%”?又该如何评价预报的结果是否准确呢?
降水的概率是气象专家根据气象条件和经验,经分析推断得到的.对“降水的概率为90%”比较合理的解释是:大量观察发现,在类似的气象条件下,大约有90%的天数要下雨.
只有根据气象预报的长期记录,才能评价预报的准确性.如果在类似气象条件下预报要下雨的那些天(天数较多)里,大约有90%确实下雨了,那么应该认为预报是准确的;如果真实下雨的天数所占的比例与90%差别较大,那么就可以认为预报不太准确.
练习(第254页)
1.判断下列说法是否正确,并说明理由:
(1)抛掷一枚硬币正面朝上的概率为0.5,则抛掷两枚硬币,一定是一次正面朝上,一次反面朝上;
(2)抛掷一枚质地均匀的硬币10次,结果是4次正面朝上,所以事件“正面朝上”的概率为0.4;
(3)当试验次数很大时,随机事件发生的频率接近其概率;
(4)在一次试验中,随机事件可能发生也可能不发生,所以事件发生和不发生的概率各是0.5.
(1)不正确.抛掷两枚硬币,“一次正面朝上,一次反面朝上”的概率是0.5,不是必然事件.
概率与频率有本质的区别.
(2)不正确.只能说频率是0.4,正面朝上的概率为
0.5.由于试验次数较少,频率与概率差别较大.
(3)正确.试验次数较大时,频率稳定到概率.
(4)不正确.随机事件发生的概率有大小之分.这种错误是
“等可能性偏见”.
2.用掷两枚硬币做胜负游戏,规定:两枚硬币同时出现正面或同时出现反面算甲胜,一个正面、一个反面算乙胜.这个游戏公平吗?
抛掷两枚质地均匀的硬币,同时出现正面或同时出现反面的概率为0.5,出现一个正面、一个反面的概率也为0.5,这个游戏是公平的.
3.据统计ABO血型具有民族和地区差异.在我国H省调査了30488人,四种血型的人数如下:
血型
A
B
O
AB
人数/人
7704
10765
8970
3049
频率
(1)计算H省各种血型的频率并填表(精确到0.001);
(2)如果从H省任意调查一个人的血型,那么他是O型血的概率大约是多少?
0.253
0.353
0.294
0.100
(2)他是O型血的概率大约是0.294
4.分别举出一个生活中概率很小和很大的例子.
例如,飞机失事是一个小概率事件,买福利彩票双色球中一等奖是小概率事件,购买一台知名品牌笔记本电脑,该电脑是合格品是一个概率很大的事件.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
