2021-2022学年沪科新版七年级上册数学《第4章 直线与角》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年沪科新版七年级上册数学《第4章 直线与角》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 272.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 06:54:30 | ||
图片预览

文档简介
2021-2022学年沪科新版七年级上册数学《第4章
直线与角》单元测试卷
一.选择题
1.下列图形属于棱柱的有( )
A.2个
B.3个
C.4个
D.5个
2.下列立体图形中是圆柱的是( )
A.
B.
C.
D.
3.如图,下列图形全部属于柱体的是( )
A.
B.
C.
D.
4.已知柱体的体积V=S?h,其中S表示柱体的底面面积,h表示柱体的高.现将矩形ABCD绕轴l旋转一周,则形成的几何体的体积等于( )
A.πr2h
B.2πr2h
C.3πr2h
D.4πr2h
5.下面几种几何图形中,属于平面图形的是( )
①三角形;②长方形;③正方体;④圆;⑤四棱锥;⑥圆柱.
A.①②④
B.①②③
C.①②⑥
D.④⑤⑥
6.下列各图中,( )是四棱柱的侧面展开图.
A.
B.
C.
D.
7.下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
A.
B.
C.
D.
8.根据图中骰子的三种不同状态显示的数字,推出?处的数字是( )
A.1
B.2
C.3
D.6
9.两个完全相同的长方体的长、宽、高分别是5cm、4cm、3cm,把它们按不同方式叠放在一起分别组成新的长方体,在这些新长方体中表面积最大的是( )
A.158cm2
B.176cm2
C.164cm2
D.188cm2
10.用一个平面去截一个几何体,截面是三角形,这个几何体不可能是( )
A.棱柱
B.圆柱
C.圆锥
D.棱锥
二.填空题
11.“枪打一条线,棍打一大片”这个现象说明:
.
12.能展开成如图所示的几何体可能是
.
13.圆锥由
个面围成,其中
个平面,
个曲面.
14.六棱柱有
面.
15.如图,在长方体ABCD﹣EFGH中,与平面ADHE垂直的棱共有
条.
16.如图,将19个棱长为a的正方体按如图摆放,则这个几何体的表面积是
.
17.如图是由6个相同的正方形拼成的图形,请你将其中一个正方形移动到合适的位置,使它与另5个正方形能拼成一个正方体的表面展开图(请在图中将要移动的那个正方形涂黑,并画出移动后的正方形)
.
18.如图,在边长为1的小正三角形组成的图形中,正六边形的个数共有
个.
19.若要使图中的展开图按虚线折叠成正方体后,相对面上两个数之和为10,则x+y=
.
20.如图是棱长为2cm的正方体,过相邻三条棱的中点截取一个小正方体,则剩下部分的表面积为
cm2.
三.解答题
21.把一个长方形绕它的一条边所在的直线旋转一周能得到一个圆柱体,那么把一个长为4cm,宽为3cm的长方形绕它的一条边所在的直线旋转一周后,得到的圆柱体的体积是多少?(结果保留π)
22.将下列几何体与它的名称连接起来.
23.如图,上面是一些具体的物体,下面是一些立体图形,试找出与下面立体图形相类似的实物(用线连接).
24.如图,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起可以构成正方体表面的不同展开图(填出三种答案).
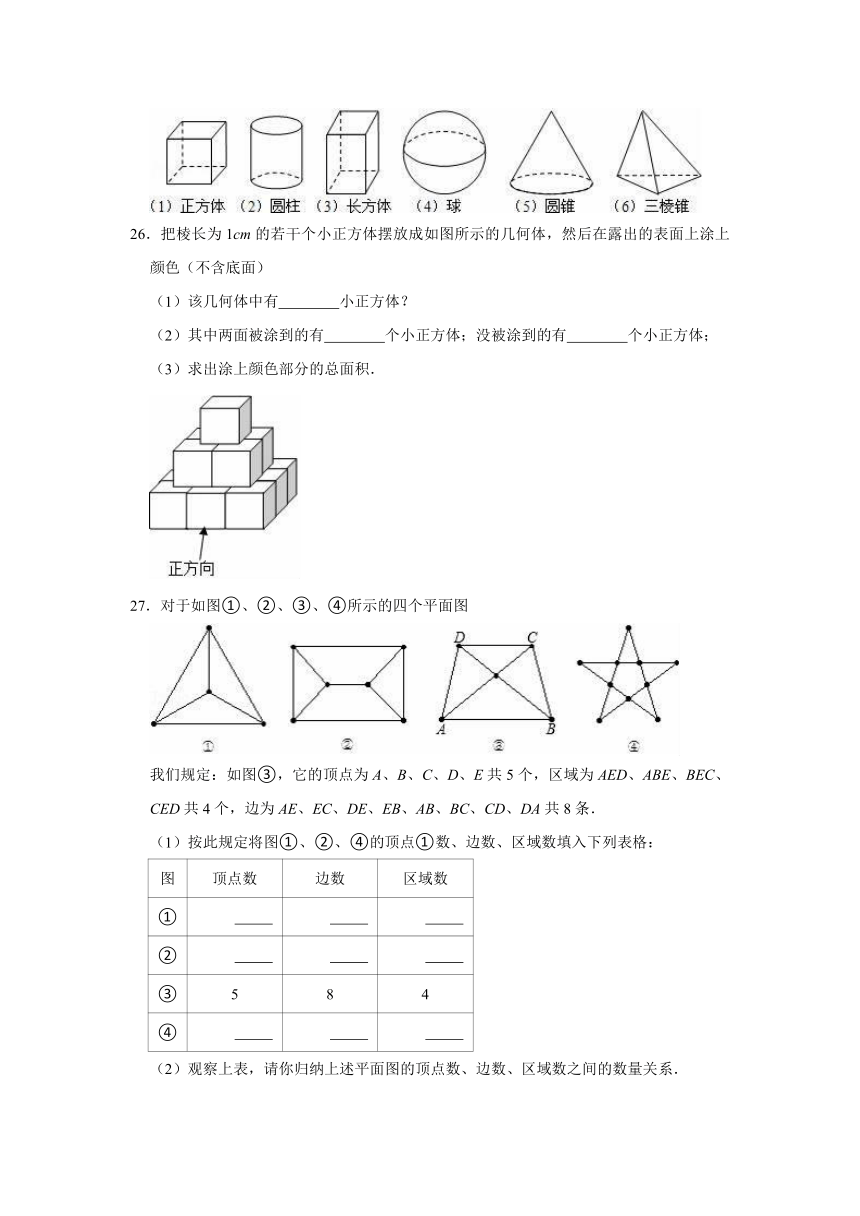
25.将下列几何体分类,并说明理由.
26.把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有
小正方体?
(2)其中两面被涂到的有
个小正方体;没被涂到的有
个小正方体;
(3)求出涂上颜色部分的总面积.
27.对于如图①、②、③、④所示的四个平面图
我们规定:如图③,它的顶点为A、B、C、D、E共5个,区域为AED、ABE、BEC、CED共4个,边为AE、EC、DE、EB、AB、BC、CD、DA共8条.
(1)按此规定将图①、②、④的顶点①数、边数、区域数填入下列表格:
图
顶点数
边数
区域数
①
②
③
5
8
4
④
(2)观察上表,请你归纳上述平面图的顶点数、边数、区域数之间的数量关系.
(3)若有一个平面图满足(2)中归纳所得的数量关系,它共有9个区域,且每一个顶点出发都有3条边,则这个平面图共有多少条边?
参考答案与试题解析
一.选择题
1.解:第一、二、四个几何体是棱柱,
故选:B.
2.解:由圆柱的特征判定D为圆柱.
故选:D.
3.解:A、左边的图形属于锥体,故本选项错误;
B、上面的图形是圆锥,属于锥体,故本选项错误;
C、三个图形都属于柱体,故本选项正确;
D、上面的图形不属于柱体,故本选项错误.
故选:C.
4.解:∵柱体的体积V=S?h,其中S表示柱体的底面面积,h表示柱体的高,现将矩形ABCD绕轴l旋转一周,
∴柱体的底面圆环面积为:π(2r)2﹣πr2=3πr2,
∴形成的几何体的体积等于:3πr2h.
故选:C.
5.解:①三角形;②长方形;④圆,它们的各部分都在同一个平面内,属于平面图形;
③正方体;⑤四棱锥;⑥圆柱属于立体图形.
故选:A.
6.解:由分析知:四棱柱的侧面展开图是矩形图;
故选:A.
7.解:根据立体图形可得,展开图中三角形图案的顶点应与圆形的图案相对,而选项A,D与此不符,所以错误;
三角形图案所在的面应与圆形的图案所在的面相邻,而选项C与此也不符,正确的是B.
故选:B.
8.解:根据图1可知,1和4,5点相邻,根据图2可知,1和2,3点相邻,
∴图3中的下面为1,
∴“?”处的数是6点.
故选:D.
9.解:根据以上分析:表面积最大的为4(5×4+4×3+5×3)﹣2×3×4=164cm2.
故选:C.
10.解:∵圆柱体的主视图只有矩形或圆,
∴如果截面是三角形,那么这个几何体不可能是圆柱.
故选:B.
二.填空题
11.解:子弹可看作一个点,棍可看作一条线,
∴“枪打一条线,棍打一大片”这个现象说明:点动成线,线动成面.
故答案为:点动成线,线动成面.
12.解:观察图形可得,这是个上底面、下底面为三角形,侧面有三个长方形的三棱柱的展开图.
故答案为:三棱柱.
13.解:圆锥的侧面为曲面,底面为平面.
∴圆锥由2个面围成,其中1个平面,1个曲面.
故答案为2,1,1.
14.解:六棱柱上下两个底面,侧面是6个长方形,所以共有8个面.
故答案为:8.
15.解:与平面ADHE垂直的棱有:AB,DC,HG,EF.共4条.
故答案为4.
16.解:从前、后、左、右、上、下方向看到的面数分别为:10,10,8,8,9,9
所以表面积为(10+10+8+8+9+9
)a2=54a2,
故答案为:54a2.
17.解:
或
或等.
18.解:小的正六边形将有6个小正三角形组成,图中可当作正六边形的中心的有7个,加上最大的这个正六边形,一共有8个.
故答案为:8.
19.解:这是一个正方体的平面展开图,共有六个面,其中面“1”与面“x”相对,面“3”与面“y”相对,
则1+x=10,3+y=10,
解得:x=9,y=7,
则x+y=16.
故答案为:16.
20.解:过相邻三条棱的中点截取一个小正方体,则剩下部分的表面积为2×2×6=24cm2.
故答案为:24.
三.解答题
21.解:绕长所在的直线旋转一周得到圆柱体积为:
π×32×4=36π(cm3),
绕宽所在的直线旋转一周得到圆柱体积为:
π×42×3=48π(cm3),
答:得到的圆柱体的体积是36πcm3或者48πcm3.
22.解:如图所示:
23.解:埃及金字塔﹣﹣(2)
西瓜﹣﹣(3)
水杯﹣﹣(1)
房屋﹣﹣(5).
24.解:根据正方体的展开图作图(答案不唯一):
25.解:答案不唯一,如
(1)按平面分:正方体,长方体,三棱锥;
(2)按曲面分:圆柱,圆锥,球.
理由是:正方体的面是六个正方形组成,长方体的面是六个长方形组成,三棱锥的面是四个三角形组成,都是平面图形;而圆柱和圆锥的侧面都是曲面,球的整个面是曲面.
26.解;(1)由图可得,
该几何体中有:1+4+9=14(个)小正方体,
故答案为:14个;
(2)由图可得,
中两面被涂到的有4个小正方体;没被涂到的有1个小正方体,
故答案为:4,1;
(3)涂上颜色部分的总面积为:1×1×(12+9+8+4)=33cm2,
即涂上颜色部分的总面积为33cm2.
27.解:(1)按此规定将图①、②、④的顶点数、边数、区域数填入下列表格:
图
顶点数
边数
区域数
①
4
6
3
②
6
9
4
③
5
8
4
④
10
15
6
(2)由表格得:顶点数+区域数=边数+1,
(3)设顶点数为x,根据题意可知,x+9=+1,
得出x=16
每个顶点发出三个3边,有9个区域数,
则有16个顶点,24条边.
直线与角》单元测试卷
一.选择题
1.下列图形属于棱柱的有( )
A.2个
B.3个
C.4个
D.5个
2.下列立体图形中是圆柱的是( )
A.
B.
C.
D.
3.如图,下列图形全部属于柱体的是( )
A.
B.
C.
D.
4.已知柱体的体积V=S?h,其中S表示柱体的底面面积,h表示柱体的高.现将矩形ABCD绕轴l旋转一周,则形成的几何体的体积等于( )
A.πr2h
B.2πr2h
C.3πr2h
D.4πr2h
5.下面几种几何图形中,属于平面图形的是( )
①三角形;②长方形;③正方体;④圆;⑤四棱锥;⑥圆柱.
A.①②④
B.①②③
C.①②⑥
D.④⑤⑥
6.下列各图中,( )是四棱柱的侧面展开图.
A.
B.
C.
D.
7.下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
A.
B.
C.
D.
8.根据图中骰子的三种不同状态显示的数字,推出?处的数字是( )
A.1
B.2
C.3
D.6
9.两个完全相同的长方体的长、宽、高分别是5cm、4cm、3cm,把它们按不同方式叠放在一起分别组成新的长方体,在这些新长方体中表面积最大的是( )
A.158cm2
B.176cm2
C.164cm2
D.188cm2
10.用一个平面去截一个几何体,截面是三角形,这个几何体不可能是( )
A.棱柱
B.圆柱
C.圆锥
D.棱锥
二.填空题
11.“枪打一条线,棍打一大片”这个现象说明:
.
12.能展开成如图所示的几何体可能是
.
13.圆锥由
个面围成,其中
个平面,
个曲面.
14.六棱柱有
面.
15.如图,在长方体ABCD﹣EFGH中,与平面ADHE垂直的棱共有
条.
16.如图,将19个棱长为a的正方体按如图摆放,则这个几何体的表面积是
.
17.如图是由6个相同的正方形拼成的图形,请你将其中一个正方形移动到合适的位置,使它与另5个正方形能拼成一个正方体的表面展开图(请在图中将要移动的那个正方形涂黑,并画出移动后的正方形)
.
18.如图,在边长为1的小正三角形组成的图形中,正六边形的个数共有
个.
19.若要使图中的展开图按虚线折叠成正方体后,相对面上两个数之和为10,则x+y=
.
20.如图是棱长为2cm的正方体,过相邻三条棱的中点截取一个小正方体,则剩下部分的表面积为
cm2.
三.解答题
21.把一个长方形绕它的一条边所在的直线旋转一周能得到一个圆柱体,那么把一个长为4cm,宽为3cm的长方形绕它的一条边所在的直线旋转一周后,得到的圆柱体的体积是多少?(结果保留π)
22.将下列几何体与它的名称连接起来.
23.如图,上面是一些具体的物体,下面是一些立体图形,试找出与下面立体图形相类似的实物(用线连接).
24.如图,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起可以构成正方体表面的不同展开图(填出三种答案).
25.将下列几何体分类,并说明理由.
26.把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有
小正方体?
(2)其中两面被涂到的有
个小正方体;没被涂到的有
个小正方体;
(3)求出涂上颜色部分的总面积.
27.对于如图①、②、③、④所示的四个平面图
我们规定:如图③,它的顶点为A、B、C、D、E共5个,区域为AED、ABE、BEC、CED共4个,边为AE、EC、DE、EB、AB、BC、CD、DA共8条.
(1)按此规定将图①、②、④的顶点①数、边数、区域数填入下列表格:
图
顶点数
边数
区域数
①
②
③
5
8
4
④
(2)观察上表,请你归纳上述平面图的顶点数、边数、区域数之间的数量关系.
(3)若有一个平面图满足(2)中归纳所得的数量关系,它共有9个区域,且每一个顶点出发都有3条边,则这个平面图共有多少条边?
参考答案与试题解析
一.选择题
1.解:第一、二、四个几何体是棱柱,
故选:B.
2.解:由圆柱的特征判定D为圆柱.
故选:D.
3.解:A、左边的图形属于锥体,故本选项错误;
B、上面的图形是圆锥,属于锥体,故本选项错误;
C、三个图形都属于柱体,故本选项正确;
D、上面的图形不属于柱体,故本选项错误.
故选:C.
4.解:∵柱体的体积V=S?h,其中S表示柱体的底面面积,h表示柱体的高,现将矩形ABCD绕轴l旋转一周,
∴柱体的底面圆环面积为:π(2r)2﹣πr2=3πr2,
∴形成的几何体的体积等于:3πr2h.
故选:C.
5.解:①三角形;②长方形;④圆,它们的各部分都在同一个平面内,属于平面图形;
③正方体;⑤四棱锥;⑥圆柱属于立体图形.
故选:A.
6.解:由分析知:四棱柱的侧面展开图是矩形图;
故选:A.
7.解:根据立体图形可得,展开图中三角形图案的顶点应与圆形的图案相对,而选项A,D与此不符,所以错误;
三角形图案所在的面应与圆形的图案所在的面相邻,而选项C与此也不符,正确的是B.
故选:B.
8.解:根据图1可知,1和4,5点相邻,根据图2可知,1和2,3点相邻,
∴图3中的下面为1,
∴“?”处的数是6点.
故选:D.
9.解:根据以上分析:表面积最大的为4(5×4+4×3+5×3)﹣2×3×4=164cm2.
故选:C.
10.解:∵圆柱体的主视图只有矩形或圆,
∴如果截面是三角形,那么这个几何体不可能是圆柱.
故选:B.
二.填空题
11.解:子弹可看作一个点,棍可看作一条线,
∴“枪打一条线,棍打一大片”这个现象说明:点动成线,线动成面.
故答案为:点动成线,线动成面.
12.解:观察图形可得,这是个上底面、下底面为三角形,侧面有三个长方形的三棱柱的展开图.
故答案为:三棱柱.
13.解:圆锥的侧面为曲面,底面为平面.
∴圆锥由2个面围成,其中1个平面,1个曲面.
故答案为2,1,1.
14.解:六棱柱上下两个底面,侧面是6个长方形,所以共有8个面.
故答案为:8.
15.解:与平面ADHE垂直的棱有:AB,DC,HG,EF.共4条.
故答案为4.
16.解:从前、后、左、右、上、下方向看到的面数分别为:10,10,8,8,9,9
所以表面积为(10+10+8+8+9+9
)a2=54a2,
故答案为:54a2.
17.解:
或
或等.
18.解:小的正六边形将有6个小正三角形组成,图中可当作正六边形的中心的有7个,加上最大的这个正六边形,一共有8个.
故答案为:8.
19.解:这是一个正方体的平面展开图,共有六个面,其中面“1”与面“x”相对,面“3”与面“y”相对,
则1+x=10,3+y=10,
解得:x=9,y=7,
则x+y=16.
故答案为:16.
20.解:过相邻三条棱的中点截取一个小正方体,则剩下部分的表面积为2×2×6=24cm2.
故答案为:24.
三.解答题
21.解:绕长所在的直线旋转一周得到圆柱体积为:
π×32×4=36π(cm3),
绕宽所在的直线旋转一周得到圆柱体积为:
π×42×3=48π(cm3),
答:得到的圆柱体的体积是36πcm3或者48πcm3.
22.解:如图所示:
23.解:埃及金字塔﹣﹣(2)
西瓜﹣﹣(3)
水杯﹣﹣(1)
房屋﹣﹣(5).
24.解:根据正方体的展开图作图(答案不唯一):
25.解:答案不唯一,如
(1)按平面分:正方体,长方体,三棱锥;
(2)按曲面分:圆柱,圆锥,球.
理由是:正方体的面是六个正方形组成,长方体的面是六个长方形组成,三棱锥的面是四个三角形组成,都是平面图形;而圆柱和圆锥的侧面都是曲面,球的整个面是曲面.
26.解;(1)由图可得,
该几何体中有:1+4+9=14(个)小正方体,
故答案为:14个;
(2)由图可得,
中两面被涂到的有4个小正方体;没被涂到的有1个小正方体,
故答案为:4,1;
(3)涂上颜色部分的总面积为:1×1×(12+9+8+4)=33cm2,
即涂上颜色部分的总面积为33cm2.
27.解:(1)按此规定将图①、②、④的顶点数、边数、区域数填入下列表格:
图
顶点数
边数
区域数
①
4
6
3
②
6
9
4
③
5
8
4
④
10
15
6
(2)由表格得:顶点数+区域数=边数+1,
(3)设顶点数为x,根据题意可知,x+9=+1,
得出x=16
每个顶点发出三个3边,有9个区域数,
则有16个顶点,24条边.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
