2021-2022学年鲁教五四新版九年级上册数学《第1章 反比例函数》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教五四新版九年级上册数学《第1章 反比例函数》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 305.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 07:06:28 | ||
图片预览



文档简介
2021-2022学年鲁教五四新版九年级上册数学《第1章
反比例函数》单元测试卷
一.选择题
1.下列函数中,是反比例函数的是( )
A.y=x﹣1
B.
C.
D.
2.已知函数y=(m﹣2)x是反比例函数,则m的值为( )
A.2
B.﹣2
C.2或﹣2
D.任意实数
3.近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知200度近视眼镜镜片的焦距为0.5m,则y与x的函数关系式为( )
A.y=
B.y=
C.y=
D.y=
4.函数y=与y=kx+k(k为常数(k≠0)在同一平面直角坐标系中的图象可能是( )
A.
B.
C.
D.
5.已知点P(x,y)满足,则经过点P的反比例函数y=的图象经过( )
A.第一、二象限
B.第三、四象限
C.第一、三象限
D.第二、四象限
6.下列函数中,y随x的增大而减小的是( )
A.
B.
C.
D.
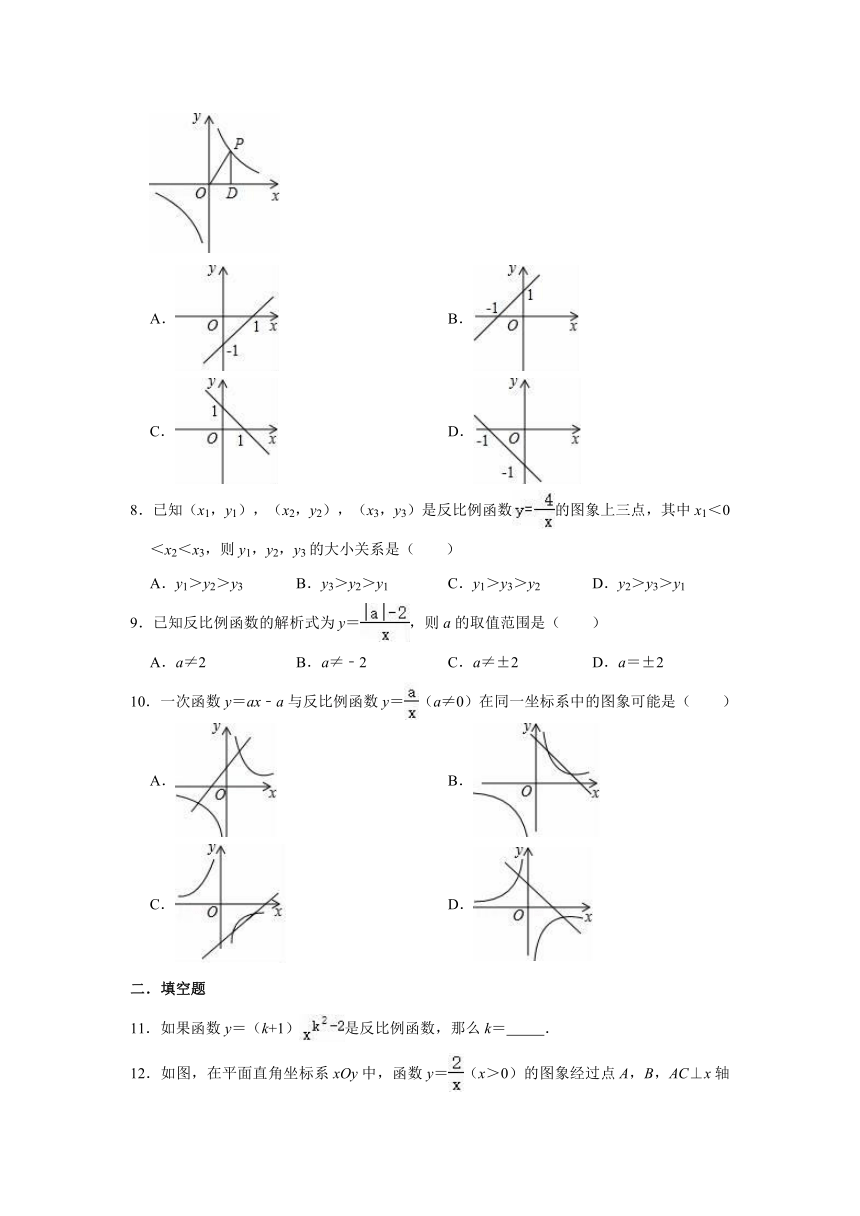
7.如图,点P为反比例函数y=上的一动点,作PD⊥x轴于点D,△POD的面积为k,则函数y=kx﹣1的图象为( )
A.
B.
C.
D.
8.已知(x1,y1),(x2,y2),(x3,y3)是反比例函数的图象上三点,其中x1<0<x2<x3,则y1,y2,y3的大小关系是( )
A.y1>y2>y3
B.y3>y2>y1
C.y1>y3>y2
D.y2>y3>y1
9.已知反比例函数的解析式为y=,则a的取值范围是( )
A.a≠2
B.a≠﹣2
C.a≠±2
D.a=±2
10.一次函数y=ax﹣a与反比例函数y=(a≠0)在同一坐标系中的图象可能是( )
A.
B.
C.
D.
二.填空题
11.如果函数y=(k+1)是反比例函数,那么k=
.
12.如图,在平面直角坐标系xOy中,函数y=(x>0)的图象经过点A,B,AC⊥x轴于点C,BD⊥y轴于点D,连接OA,OB,则△OAC与△OBD的面积之和为
.
13.近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知500度的近视眼镜镜片的焦距是0.2m,则y与x之间的函数关系式是
.
14.如图,是反比例函数y=的图象的一个分支,对于给出的下列说法:
①常数k的取值范围是k>2;
②另一个分支在第三象限;
③在函数图象上取点A(a1,b1)和点B(a2,b2),当a1>a2时,则b1<b2;
④在函数图象的某一个分支上取点A(a1,b1)和点B(a2,b2),当a1>a2时,则b1<b2;
其中正确的是
(在横线上填出正确的序号)
15.如图,函数y1=x(x≥0),y2=(x>0)的图象相交于点A(2,2),则当x满足
时,函数值y1>y2.
16.如图,反比例函数y=(k<0)的图象与⊙O相交,某同学在⊙O内做随机扎针实验,针头落在阴影区域内的概率为
.
17.已知(﹣2,y1),(﹣1,y2),(3,y3)是反比例函数的图象上的三个点,则y1,y2,y3的大小关系是
.
18.若双曲线y=(2m﹣1)的图象在第一、三象限,则函数的解析式为
.
19.已知y=(a﹣1)是反比例函数,则a=
.
20.若反比例函数的图象经过第一、三象限,则
k的取值范围是
.
三.解答题
21.已知函数是反比例函数,求k的值.
22.已知正比例函数y=x和反比例函数的图象(如图),请你画出函数的大致图象,并用文字说明所画图象的特征.
23.已知y=y1+y2,y1与(x﹣1)成正比例,y2与(x+1)成反比例,当x=0时,y=﹣3,当x=1时,y=﹣1.
(1)求y的表达式;
(2)求当x=时y的值.
24.已知经过闭合电路的电流I与电路的电阻R是反比例函数关系,请根据表格已知条件求出I与R的反比例函数关系式,并填写表格中的空格.
I(安)
5
10
R(欧)
10
25.如图,是反比例函数y=的图象的一支.根据给出的图象回答下列问题:
(1)该函数的图象位于哪几个象限?请确定m的取值范围;
(2)在这个函数图象的某一支上取点A(x1,y1)、B(x2,y2).如果y1<y2,那么x1与x2有怎样的大小关系?
26.下列函数中,哪些表示y是x的反比例函数:(1)y=;(2)y=;(3)xy=6;(4)3x+y=0;(5)x﹣2y=1;(6)3xy+2=0.
参考答案与试题解析
一.选择题
1.解:A、是一次函数,故选项错误;
B、不符合y=的形式,故选项错误;
C、正确;
D、不符合y=的形式,是正比例函数,故选项错误.
故选:C.
2.解:∵函数y=(m﹣2)x是反比例函数,
∴,
解得:m=﹣2.
故选:B.
3.解:由题意设y=,
由于点(0.5,200)适合这个函数解析式,则k=0.5×200=100,
∴y=.
故眼镜度数y与镜片焦距x之间的函数关系式为:y=.
故选:A.
4.解:①当k>0时,y=kx+k过一、二、三象限;函数y=过一、三象限;
②当k<0时,y=kx+k过二、三、四象象限;函数y=过二、四象限.
观察图形可知只有A符合.
故选:A.
5.解:∵x﹣2011≥0,2011﹣x≥0,
∴x=2011,
∴y=,
将x=2011,y=代入y=得,m=1,
所以反比例函数y=的图象位于第一、三象限.
故选:C.
6.解:A、∵正比例函数y=x中,k=>0,∴y随x的增大而增大,故本选项错误;
B、∵正比例函数y=﹣x中,k=﹣<0,∴y随x的增大而减小,故本选项正确;
C、∵反比例函数y=中,k=3>0,∴函数图象在每一象限内y随x的增大而减小,故本选项错误;
D、∵反比例函数y=﹣中,k=﹣3>0,∴函数图象在每一象限内y随x的增大而增大,故本选项错误.
故选:B.
7.解:设P点坐标为(x,y),
∵P点在第一象限且在函数y=的图象上,
∴xy=2,
∴S△OPD=xy=×2=1,即k=1.
∴一次函数y=kx﹣1的解析式为:y=x﹣1,
∴一次函数的图象经过点(0,﹣1),(1,0)的直线.
故选:A.
8.解:∵反比例函数中k=﹣4<0,
∴此函数的图象在二、四象限,且在每一各象限内y随x的增大而增大,
∵x1<0<x2<x3,
∴(x1,y1)在第二象限,(x2,y2),(x3,y3)在第四象限,
∴y1>0,y2<y3<0,即y1>y3>y2.
故选:C.
9.解:根据反比例函数解析式中k是常数,不能等于0,由题意可得:|a|﹣2≠0,
解得:a≠±2,
故选:C.
10.解:A、由函数y=ax﹣a的图象可知a>0,﹣a>0,由函数y=(a≠0)的图象可知a>0,矛盾,错误;
B、由函数y=ax﹣a的图象可知a<0,由函数y=(a≠0)的图象可知a>0,相矛盾,故错误;
C、由函数y=ax﹣a的图象可知a>0,由函数y=(a≠0)的图象可知a<0,故错误;
D、由函数y=ax﹣a的图象可知a<0,﹣a>0,由函数y=(a≠0)的图象可知a<0,故正确;
故选:D.
二.填空题
11.解:根据题意k2﹣2=﹣1,解得k=±1;
又k+1≠0,则k≠﹣1;
所以k=1.
故答案为:1.
12.解:∵函数y=(x>0)的图象经过点A,B,AC⊥x轴于点C,BD⊥y轴于点D,
∴S△OAC=S△OBD=×2=1,
∴S△OAC+S△OBD=1+1=2.
故答案为2.
13.解:设y=,
∵500度的近视眼镜镜片的焦距是0.2m,
∴500=,
k=100.
∴y=.
故答案为:y=.
14.解:①根据函数图象在第一象限可得k﹣2>0,故k>2,故①正确;
②根据反比例函数的性质可得,另一个分支在第三象限,故②正确;
③根据反比例函数的性质,图象在第一、三象限时,在图象的每一支上y随x的增大而减小,A、B不一定在图象的同一支上,故③错误;
④根据反比例函数的性质,图象在第一、三象限时,在图象的每一支上y随x的增大而减小,故在函数图象的某一个分支上取点A(a1,b1)和点B(a2,b2),当a1>a2时,则b1<b2正确;
故答案为:①②④.
15.解:由题意得:函数y1=x(x≥0),y2=(x>0)的图象相交于点A(2,2),
则由图象可看出,当x>2时,函数值y1>y2.
16.解:因为阴影区域内的面积等于圆心角为90度的扇形面积,
所以针头落在阴影区域内的概率=.
故答案为.
17.解:∵反比例函数的k=﹣6<0,
∴函数图象的两个分式分别位于二、四象限,且在每一象限内y随x的增大而增大.
∵﹣2<0,﹣1<0,
∴点(﹣2,y1),(﹣1,y2)位于第二象限,
∴y1>0,y2>0,
∵﹣1>﹣2<0,
∴0<y1<y2.
∵2>0,
∴点(2,y3)位于第四象限,
∴y3<0,
∴y3<y1<y2.
故答案为:y3<y1<y2.
18.解:∵双曲线y=(2m﹣1)的图象在第一、三象限,
∴2m﹣1>0且m2﹣2=﹣1,
解得m=1.
∴2m﹣1=1,
∴函数的解析式为y=.
故答案为:y=.
19.解:根据题意,a2﹣2=﹣1,a=±1,又a≠1,所以a=﹣1.
故答案为:﹣1.
20.解:∵反比例函数的图象经过第一、三象限,
∴1﹣3k≥0,解得k<.
故答案为:k<.
三.解答题
21.解:∵是反比例函数,
∴k2﹣k﹣3=﹣1且k﹣2≠0,
解得:k=﹣1.
22.解:列表:
x
﹣3
﹣2
﹣1
﹣
1
2
3
y
﹣
﹣
0
﹣
0
描点、连线:
所画图象有两个分支,两个分支关于原点对称且都不与y轴相交.
23.解:(1)∵y1与(x﹣1)成正比例,y2与(x+1)成反比例,
∴y1=k1(x﹣1),y2=,
∵y=y1+y2,当x=0时,y=﹣3,当x=1时,y=﹣1.
∴,
∴k2=﹣2,k1=1,
∴y=x﹣1﹣;
(2)当x=﹣,y=x﹣1﹣=﹣﹣1﹣=﹣.
24.解:依题意设,
把I=10,R=10代入得:,
解得U=100,
所以.
100÷5=20.
I(安)
5
10
R(欧)
20
10
25.解:(1)∵反比例函数图象关于原点对称,图中反比例函数图象位于第四象限,
∴函数图象位于第二、四象限,则m﹣5<0,
解得,m<5,即m的取值范围是m<5;
(2)由(1)知,函数图象位于第二、四象限.所以在每一个象限内,函数值y随自变量x增大而增大.
①当y1<y2<0时,x1<x2.
②当0<y1<y2,x1<x2.
③当y1<0<y2时,x2<x1.
26.解:(1)y=不是反比例函数.
(2)∵y=,
∴xy=.
∴y=,是反比例函数.
(3)∵xy=6,
∴y=,是反比例函数.
(4)∵3x+y=0,
∴y=﹣3x,不是反比例函数.
(5)∵x﹣2y=1,
∴2y=x﹣1.
∴y=x﹣,不是反比例函数.
(6)∵3xy+2=0,
∴xy=﹣.
∴y=,是反比例函数.
反比例函数》单元测试卷
一.选择题
1.下列函数中,是反比例函数的是( )
A.y=x﹣1
B.
C.
D.
2.已知函数y=(m﹣2)x是反比例函数,则m的值为( )
A.2
B.﹣2
C.2或﹣2
D.任意实数
3.近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知200度近视眼镜镜片的焦距为0.5m,则y与x的函数关系式为( )
A.y=
B.y=
C.y=
D.y=
4.函数y=与y=kx+k(k为常数(k≠0)在同一平面直角坐标系中的图象可能是( )
A.
B.
C.
D.
5.已知点P(x,y)满足,则经过点P的反比例函数y=的图象经过( )
A.第一、二象限
B.第三、四象限
C.第一、三象限
D.第二、四象限
6.下列函数中,y随x的增大而减小的是( )
A.
B.
C.
D.
7.如图,点P为反比例函数y=上的一动点,作PD⊥x轴于点D,△POD的面积为k,则函数y=kx﹣1的图象为( )
A.
B.
C.
D.
8.已知(x1,y1),(x2,y2),(x3,y3)是反比例函数的图象上三点,其中x1<0<x2<x3,则y1,y2,y3的大小关系是( )
A.y1>y2>y3
B.y3>y2>y1
C.y1>y3>y2
D.y2>y3>y1
9.已知反比例函数的解析式为y=,则a的取值范围是( )
A.a≠2
B.a≠﹣2
C.a≠±2
D.a=±2
10.一次函数y=ax﹣a与反比例函数y=(a≠0)在同一坐标系中的图象可能是( )
A.
B.
C.
D.
二.填空题
11.如果函数y=(k+1)是反比例函数,那么k=
.
12.如图,在平面直角坐标系xOy中,函数y=(x>0)的图象经过点A,B,AC⊥x轴于点C,BD⊥y轴于点D,连接OA,OB,则△OAC与△OBD的面积之和为
.
13.近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知500度的近视眼镜镜片的焦距是0.2m,则y与x之间的函数关系式是
.
14.如图,是反比例函数y=的图象的一个分支,对于给出的下列说法:
①常数k的取值范围是k>2;
②另一个分支在第三象限;
③在函数图象上取点A(a1,b1)和点B(a2,b2),当a1>a2时,则b1<b2;
④在函数图象的某一个分支上取点A(a1,b1)和点B(a2,b2),当a1>a2时,则b1<b2;
其中正确的是
(在横线上填出正确的序号)
15.如图,函数y1=x(x≥0),y2=(x>0)的图象相交于点A(2,2),则当x满足
时,函数值y1>y2.
16.如图,反比例函数y=(k<0)的图象与⊙O相交,某同学在⊙O内做随机扎针实验,针头落在阴影区域内的概率为
.
17.已知(﹣2,y1),(﹣1,y2),(3,y3)是反比例函数的图象上的三个点,则y1,y2,y3的大小关系是
.
18.若双曲线y=(2m﹣1)的图象在第一、三象限,则函数的解析式为
.
19.已知y=(a﹣1)是反比例函数,则a=
.
20.若反比例函数的图象经过第一、三象限,则
k的取值范围是
.
三.解答题
21.已知函数是反比例函数,求k的值.
22.已知正比例函数y=x和反比例函数的图象(如图),请你画出函数的大致图象,并用文字说明所画图象的特征.
23.已知y=y1+y2,y1与(x﹣1)成正比例,y2与(x+1)成反比例,当x=0时,y=﹣3,当x=1时,y=﹣1.
(1)求y的表达式;
(2)求当x=时y的值.
24.已知经过闭合电路的电流I与电路的电阻R是反比例函数关系,请根据表格已知条件求出I与R的反比例函数关系式,并填写表格中的空格.
I(安)
5
10
R(欧)
10
25.如图,是反比例函数y=的图象的一支.根据给出的图象回答下列问题:
(1)该函数的图象位于哪几个象限?请确定m的取值范围;
(2)在这个函数图象的某一支上取点A(x1,y1)、B(x2,y2).如果y1<y2,那么x1与x2有怎样的大小关系?
26.下列函数中,哪些表示y是x的反比例函数:(1)y=;(2)y=;(3)xy=6;(4)3x+y=0;(5)x﹣2y=1;(6)3xy+2=0.
参考答案与试题解析
一.选择题
1.解:A、是一次函数,故选项错误;
B、不符合y=的形式,故选项错误;
C、正确;
D、不符合y=的形式,是正比例函数,故选项错误.
故选:C.
2.解:∵函数y=(m﹣2)x是反比例函数,
∴,
解得:m=﹣2.
故选:B.
3.解:由题意设y=,
由于点(0.5,200)适合这个函数解析式,则k=0.5×200=100,
∴y=.
故眼镜度数y与镜片焦距x之间的函数关系式为:y=.
故选:A.
4.解:①当k>0时,y=kx+k过一、二、三象限;函数y=过一、三象限;
②当k<0时,y=kx+k过二、三、四象象限;函数y=过二、四象限.
观察图形可知只有A符合.
故选:A.
5.解:∵x﹣2011≥0,2011﹣x≥0,
∴x=2011,
∴y=,
将x=2011,y=代入y=得,m=1,
所以反比例函数y=的图象位于第一、三象限.
故选:C.
6.解:A、∵正比例函数y=x中,k=>0,∴y随x的增大而增大,故本选项错误;
B、∵正比例函数y=﹣x中,k=﹣<0,∴y随x的增大而减小,故本选项正确;
C、∵反比例函数y=中,k=3>0,∴函数图象在每一象限内y随x的增大而减小,故本选项错误;
D、∵反比例函数y=﹣中,k=﹣3>0,∴函数图象在每一象限内y随x的增大而增大,故本选项错误.
故选:B.
7.解:设P点坐标为(x,y),
∵P点在第一象限且在函数y=的图象上,
∴xy=2,
∴S△OPD=xy=×2=1,即k=1.
∴一次函数y=kx﹣1的解析式为:y=x﹣1,
∴一次函数的图象经过点(0,﹣1),(1,0)的直线.
故选:A.
8.解:∵反比例函数中k=﹣4<0,
∴此函数的图象在二、四象限,且在每一各象限内y随x的增大而增大,
∵x1<0<x2<x3,
∴(x1,y1)在第二象限,(x2,y2),(x3,y3)在第四象限,
∴y1>0,y2<y3<0,即y1>y3>y2.
故选:C.
9.解:根据反比例函数解析式中k是常数,不能等于0,由题意可得:|a|﹣2≠0,
解得:a≠±2,
故选:C.
10.解:A、由函数y=ax﹣a的图象可知a>0,﹣a>0,由函数y=(a≠0)的图象可知a>0,矛盾,错误;
B、由函数y=ax﹣a的图象可知a<0,由函数y=(a≠0)的图象可知a>0,相矛盾,故错误;
C、由函数y=ax﹣a的图象可知a>0,由函数y=(a≠0)的图象可知a<0,故错误;
D、由函数y=ax﹣a的图象可知a<0,﹣a>0,由函数y=(a≠0)的图象可知a<0,故正确;
故选:D.
二.填空题
11.解:根据题意k2﹣2=﹣1,解得k=±1;
又k+1≠0,则k≠﹣1;
所以k=1.
故答案为:1.
12.解:∵函数y=(x>0)的图象经过点A,B,AC⊥x轴于点C,BD⊥y轴于点D,
∴S△OAC=S△OBD=×2=1,
∴S△OAC+S△OBD=1+1=2.
故答案为2.
13.解:设y=,
∵500度的近视眼镜镜片的焦距是0.2m,
∴500=,
k=100.
∴y=.
故答案为:y=.
14.解:①根据函数图象在第一象限可得k﹣2>0,故k>2,故①正确;
②根据反比例函数的性质可得,另一个分支在第三象限,故②正确;
③根据反比例函数的性质,图象在第一、三象限时,在图象的每一支上y随x的增大而减小,A、B不一定在图象的同一支上,故③错误;
④根据反比例函数的性质,图象在第一、三象限时,在图象的每一支上y随x的增大而减小,故在函数图象的某一个分支上取点A(a1,b1)和点B(a2,b2),当a1>a2时,则b1<b2正确;
故答案为:①②④.
15.解:由题意得:函数y1=x(x≥0),y2=(x>0)的图象相交于点A(2,2),
则由图象可看出,当x>2时,函数值y1>y2.
16.解:因为阴影区域内的面积等于圆心角为90度的扇形面积,
所以针头落在阴影区域内的概率=.
故答案为.
17.解:∵反比例函数的k=﹣6<0,
∴函数图象的两个分式分别位于二、四象限,且在每一象限内y随x的增大而增大.
∵﹣2<0,﹣1<0,
∴点(﹣2,y1),(﹣1,y2)位于第二象限,
∴y1>0,y2>0,
∵﹣1>﹣2<0,
∴0<y1<y2.
∵2>0,
∴点(2,y3)位于第四象限,
∴y3<0,
∴y3<y1<y2.
故答案为:y3<y1<y2.
18.解:∵双曲线y=(2m﹣1)的图象在第一、三象限,
∴2m﹣1>0且m2﹣2=﹣1,
解得m=1.
∴2m﹣1=1,
∴函数的解析式为y=.
故答案为:y=.
19.解:根据题意,a2﹣2=﹣1,a=±1,又a≠1,所以a=﹣1.
故答案为:﹣1.
20.解:∵反比例函数的图象经过第一、三象限,
∴1﹣3k≥0,解得k<.
故答案为:k<.
三.解答题
21.解:∵是反比例函数,
∴k2﹣k﹣3=﹣1且k﹣2≠0,
解得:k=﹣1.
22.解:列表:
x
﹣3
﹣2
﹣1
﹣
1
2
3
y
﹣
﹣
0
﹣
0
描点、连线:
所画图象有两个分支,两个分支关于原点对称且都不与y轴相交.
23.解:(1)∵y1与(x﹣1)成正比例,y2与(x+1)成反比例,
∴y1=k1(x﹣1),y2=,
∵y=y1+y2,当x=0时,y=﹣3,当x=1时,y=﹣1.
∴,
∴k2=﹣2,k1=1,
∴y=x﹣1﹣;
(2)当x=﹣,y=x﹣1﹣=﹣﹣1﹣=﹣.
24.解:依题意设,
把I=10,R=10代入得:,
解得U=100,
所以.
100÷5=20.
I(安)
5
10
R(欧)
20
10
25.解:(1)∵反比例函数图象关于原点对称,图中反比例函数图象位于第四象限,
∴函数图象位于第二、四象限,则m﹣5<0,
解得,m<5,即m的取值范围是m<5;
(2)由(1)知,函数图象位于第二、四象限.所以在每一个象限内,函数值y随自变量x增大而增大.
①当y1<y2<0时,x1<x2.
②当0<y1<y2,x1<x2.
③当y1<0<y2时,x2<x1.
26.解:(1)y=不是反比例函数.
(2)∵y=,
∴xy=.
∴y=,是反比例函数.
(3)∵xy=6,
∴y=,是反比例函数.
(4)∵3x+y=0,
∴y=﹣3x,不是反比例函数.
(5)∵x﹣2y=1,
∴2y=x﹣1.
∴y=x﹣,不是反比例函数.
(6)∵3xy+2=0,
∴xy=﹣.
∴y=,是反比例函数.
