2021-2022学年鲁教五四新版七年级上册数学《第1章 三角形》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教五四新版七年级上册数学《第1章 三角形》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 256.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 07:11:34 | ||
图片预览


文档简介
2021-2022学年鲁教五四新版七年级上册数学《第1章
三角形》单元测试卷
一.选择题
1.下列说法正确的是( )
A.一个钝角三角形一定不是等腰三角形,也不是等边三角形
B.一个等腰三角形一定是锐角三角形,或直角三角形
C.一个直角三角形一定不是等腰三角形,也不是等边三角形
D.一个等边三角形一定不是钝角三角形,也不是直角三角形
2.在下列各图的△ABC中,正确画出AC边上的高的图形是( )
A.
B.
C.
D.
3.如图,AD是△ABC的中线,DE是△ADC的高线,AB=3,AC=5,DE=2,那么点D到AB的距离是( )
A.
B.
C.
D.2
4.在下列四组线段中,能组成三角形的是( )
A.2,2,5
B.3,7,10
C.3,5,9
D.4,5,7
5.如图所示,在△ABC中,∠ACB是钝角,让点C在射线BD上向右移动,则( )
A.△ABC将先变成直角三角形,然后再变成锐角三角形,而不会再是钝角三角形
B.△ABC将变成锐角三角形,而不会再是钝角三角形
C.△ABC将先变成直角三角形,然后再变成锐角三角形,接着又由锐角三角形变为钝角三角形
D.△ABC先由钝角三角形变为直角三角形,再变为锐角三角形,接着又变为直角三角形,然后再次变为钝角三角形
6.三角形三条中线的交点叫做三角形的( )
A.内心
B.外心
C.中心
D.重心
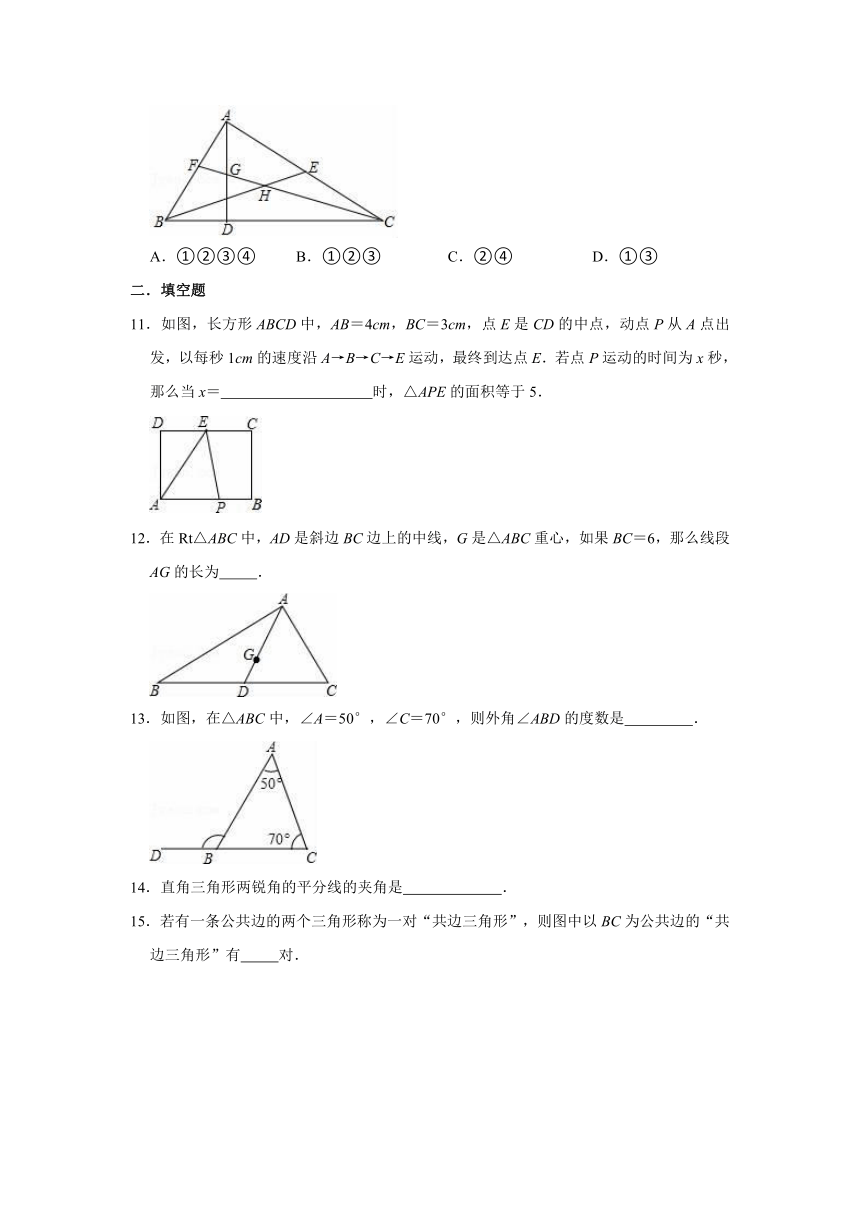
7.如图,△BEF的内角∠EBF平分线BD与外角∠AEF的平分线交于点D,过D作DH∥BC分别交EF、EB于G、H两点.下列结论:①S△EBD:S△FBD=BE:BF;②∠EFD=∠CFD;③HD=HF;④BH﹣GF=HG,其中正确的结论有( )
A.只有①②③
B.只有①②④
C.只有③④
D.①②③④
8.给出下列说法:(1)等边三角形是等腰三角形;(2)三角形按边的相等关系分类可分为等腰三角形、等边三角形和不等边三角形;(3)三角形按角的大小分类可分为锐角三角形、直角三角形和钝角三角形.其中,正确的有( )个.
A.1
B.2
C.3
D.0
9.如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;
②∠AEF=∠AFE;
③∠EBC=∠C;④AG⊥EF.正确结论有( )
A.1个
B.2个
C.3个
D.4个
10.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
①△ABE的面积=△BCE的面积;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.
A.①②③④
B.①②③
C.②④
D.①③
二.填空题
11.如图,长方形ABCD中,AB=4cm,BC=3cm,点E是CD的中点,动点P从A点出发,以每秒1cm的速度沿A→B→C→E运动,最终到达点E.若点P运动的时间为x秒,那么当x=
时,△APE的面积等于5.
12.在Rt△ABC中,AD是斜边BC边上的中线,G是△ABC重心,如果BC=6,那么线段AG的长为
.
13.如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是
.
14.直角三角形两锐角的平分线的夹角是
.
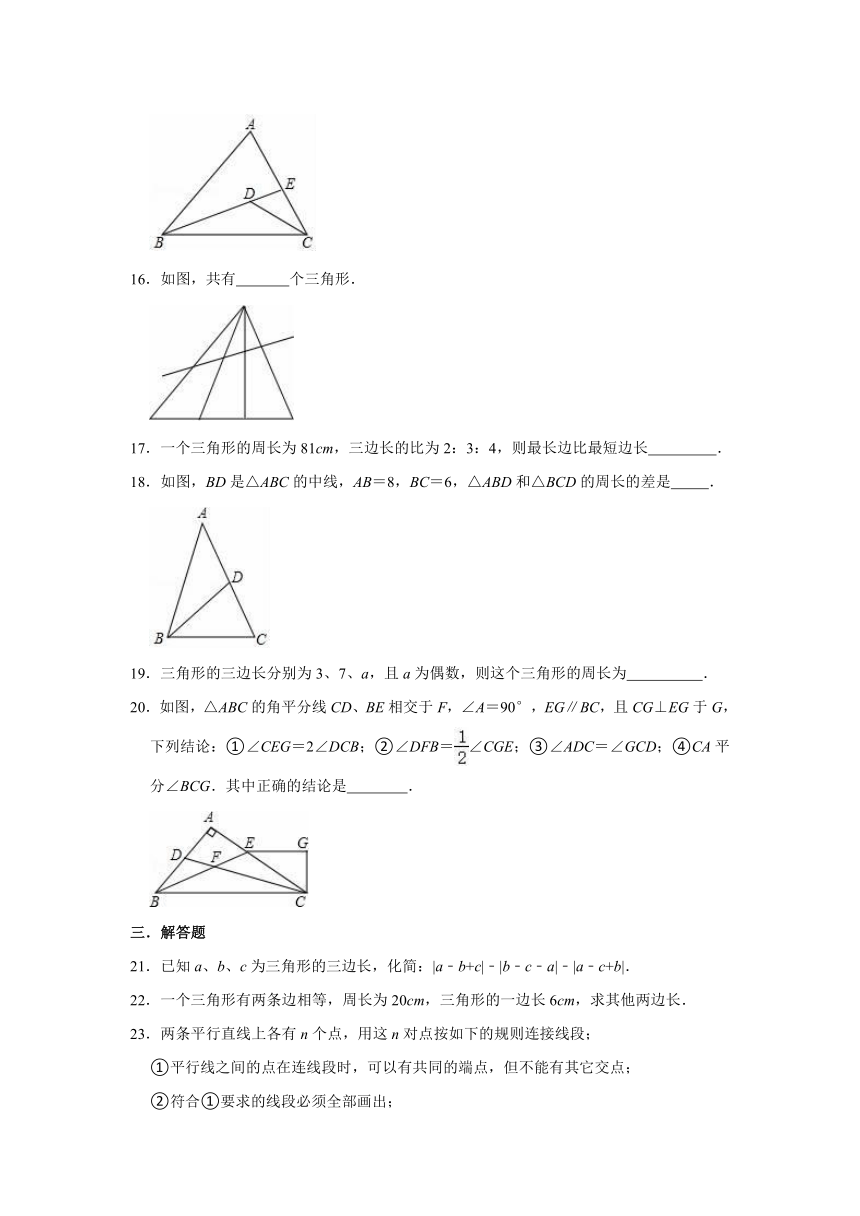
15.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有
对.
16.如图,共有
个三角形.
17.一个三角形的周长为81cm,三边长的比为2:3:4,则最长边比最短边长
.
18.如图,BD是△ABC的中线,AB=8,BC=6,△ABD和△BCD的周长的差是
.
19.三角形的三边长分别为3、7、a,且a为偶数,则这个三角形的周长为
.
20.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠DFB=∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的结论是
.
三.解答题
21.已知a、b、c为三角形的三边长,化简:|a﹣b+c|﹣|b﹣c﹣a|﹣|a﹣c+b|.
22.一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
23.两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
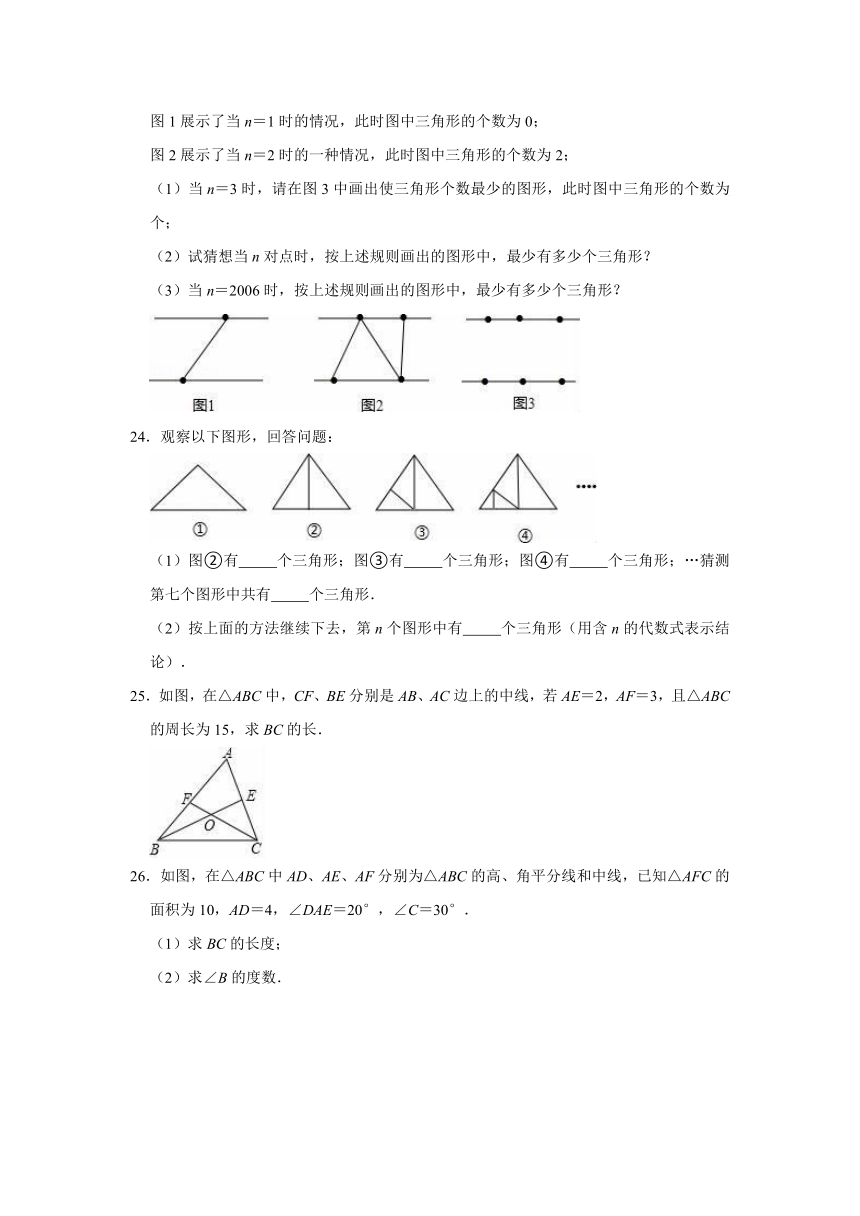
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为
个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?
24.观察以下图形,回答问题:
(1)图②有
个三角形;图③有
个三角形;图④有
个三角形;…猜测第七个图形中共有
个三角形.
(2)按上面的方法继续下去,第n个图形中有
个三角形(用含n的代数式表示结论).
25.如图,在△ABC中,CF、BE分别是AB、AC边上的中线,若AE=2,AF=3,且△ABC的周长为15,求BC的长.
26.如图,在△ABC中AD、AE、AF分别为△ABC的高、角平分线和中线,已知△AFC的面积为10,AD=4,∠DAE=20°,∠C=30°.
(1)求BC的长度;
(2)求∠B的度数.
27.如图,在△ABC中,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O.
(1)BO与OD的长度有什么关系?并证明你的结论.
(2)BC边上的中线是否一定过点O?为什么?
参考答案与试题解析
一.选择题
1.解:A、一个钝角三角形不一定不是等腰三角形,一定不是等边三角形,故本选项错误;
B、一个等腰三角形不一定是锐角三角形,或直角三角形,故本选项错误;
C、一个直角三角形不一定不是等腰三角形,一定不是等边三角形,故本选项错误;
D、一个等边三角形一定不是钝角三角形,也不是直角三角形,故本选项正确;
故选:D.
2.解:AC边上的高就是过B作垂线垂直AC交AC于某点,因此只有C符合条件,故选C.
3.解:∵AC=5,DE=2,
∴△ADC的面积为=5,
∵AD是△ABC的中线,
∴△ABD的面积为5,
∴点D到AB的距离是.
故选:A.
4.解:A、∵2+2=4<5,
∴2,2,5不能组成三角形,故本选项错误;
B、∵3+7=10,
∴3,7,10不能组成三角形,故本选项错误;
C、∵3+5=8<9,
∴3,5,9不能组成三角形,故本选项错误;
D、4,5,7能组成三角形,故本选项正确.
故选:D.
5.解:根据∠A的旋转变化规律可知:△ABC先由钝角三角形变为直角三角形,再变为锐角三角形,接着又变为直角三角形,然后再次变为钝角三角形.
故选:D.
6.解:三角形的重心是三角形三条中线的交点.
故选:D.
7.解:过D作DM⊥AB,DN⊥CB,DO⊥EF,
①正确.
因为S△EBD=?BE?DM,S△FBD=?BF?DN,
因为BD是∠EBC的平分线,DM⊥AB,DN⊥CB,
所以DM=DN,
所以S△EBD:S△FBD=BE:BF;
②正确.
∵DE是∠AEF的平分线,
∴AD=DO,
∵DB是∠ABC的平分线,
∴DA=DN,
∴DO=DN,
∴DF是∠EFC的平分线,
∴∠EFD=∠CFD;
③错误.
因为HD∥BF,
所以∠HDB=∠FBD,
又因为BD平分∠ABC,
所以∠HBD=∠CBD,
于是∠HBD=∠HDB,
故HB=HD.
但没有条件说明HF与HB必然相等;
④正确.
由于点D为△BEF的内角∠EBF平分线BD与外角∠AEF的平分线的交点,
故D为△BEF的内心,
于是FD为∠EFC的平分线,
故∠CFD=∠EFD,
又因为DH∥BC,
所以∠HDF=∠CFD,
故∠GDF=∠DFE,
于是GF=GD,
又因为HB=HD,
所以HD﹣GD=HG,
即BH﹣GF=HG.
故①②④正确.
故选:B.
8.解:(1)等边三角形是一特殊的等腰三角形,正确;
(2)三角形按边分类可以分为不等边三角形和等腰三角形,错误;
(3)三角形按角分类应分为锐角三角形、直角三角形和钝角三角形,正确.
综上所述,正确的结论2个.
故选:B.
9.解:∵∠BAC=90°,AD⊥BC,
∴∠C+∠ABC=90°,
∠BAD+∠ABC=90°,
∴∠BAD=∠C,故①正确;
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∵∠ABE+∠AEF=90°,
∠CBE+∠BFD=90°,
∴∠AEF=∠BFD,
又∵∠AFE=∠BFD(对顶角相等),
∴∠AEF=∠AFE,故②正确;
∵∠ABE=∠CBE,
∴只有∠C=30°时∠EBC=∠C,故③错误;
∵∠AEF=∠AFE,
∴AE=AF,
∵AG平分∠DAC,
∴AG⊥EF,故④正确.
综上所述,正确的结论是①②④.
故选:C.
10.解:∵BE是中线,
∴AE=CE,
∴△ABE的面积=△BCE的面积(等底等高的三角形的面积相等),故①正确;
∵CF是角平分线,
∴∠ACF=∠BCF,
∵AD为高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,
∴∠ABC=∠CAD,
∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,
∴∠AFG=∠AGF,故②正确;
∵AD为高,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,
∴∠ACB=∠BAD,
∵CF是∠ACB的平分线,
∴∠ACB=2∠ACF,
∴∠BAD=2∠ACF,
即∠FAG=2∠ACF,故③正确;
根据已知条件不能推出∠HBC=∠HCB,即不能推出BH=CH,故④错误;
故选:B.
二.填空题
11.解:①如图1,
当P在AB上时,
∵△APE的面积等于5,
∴x?3=5,
x=;
②当P在BC上时,
∵△APE的面积等于5,
∴S长方形ABCD﹣S△CPE﹣S△ADE﹣S△ABP=5,
∴3×4﹣(3+4﹣x)×2﹣×2×3﹣×4×(x﹣4)=5,
x=5;
③当P在CE上时,
∴(4+3+2﹣x)×3=5,
x=<3+4,此时不符合;
故答案为:或5.
12.解:∵AD是斜边BC边上的中线,
∴AD=BC=×6=3,
∵G是△ABC重心,
∴=2,
∴AG=AD=×3=2.
故答案为2.
13.解:∵∠A=50°,∠C=70°,
∴∠ABD=∠A+∠C=120°,
故答案为:120°.
14.解:如图,∠ABC+∠BAC=90°,
∵AD、BE分别是∠BAC和∠ABC的角平分线,
∴∠OAB+∠OBA=(∠ABC+∠BAC)=45°,
∴∠AOE=∠OAB+∠OBA=45°,
∴∠AOB=135°
∴两锐角的平分线的夹角是45°或135°.
故答案为:45°或135°.
15.解:△BDC与△BEC、△BDC与△BAC、△BEC与△BAC共三对.
故答案为:3.
16.解:上半部分:单个的三角形有3个,复合的三角形有2+1=3个,
所以上半部分三角形的个数为3+3=6个,
同理考虑横截线的三角形的个数也是6个.
故共有12个三角形.
17.解:设三角形的三边长为2x,3x,4x,
由题意得,2x+3x+4x=81,
解得:x=9,
则三角形的三边长分别为:18cm,27cm,36cm,
所以,最长边比最短边长:36﹣18=18(cm).
故答案是:18cm.
18.解:∵BD是△ABC的中线,
∴AD=CD,
∴△ABD和△BCD的周长差=(AB+AD+BD)﹣(BC+CD+BD),
=AB+AD+BD﹣BC﹣CD﹣BD,
=AB﹣BC,
∵AB=8,BC=6,
∴△ABD和△BCD的周长差=8﹣6=2.
答:△ABD和△BCD的周长差为2.
故答案为:2
19.解:∵7﹣3<a<7+3,
∴4<a<10,
又∵第三边是偶数,
∴a的值:6或8;
∴三角形的周长为:3+6+7=16或3+8+7=18.
故答案为:16或18.
20.解:①∵EG∥BC,
∴∠CEG=∠ACB,
又∵CD是△ABC的角平分线,
∴∠CEG=∠ACB=2∠DCB,故正确;
④无法证明CA平分∠BCG,故错误;
③∵∠A=90°,
∴∠ADC+∠ACD=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ADC+∠BCD=90°.
∵EG∥BC,且CG⊥EG,
∴∠GCB=90°,即∠GCD+∠BCD=90°,
∴∠ADC=∠GCD,故正确;
②∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,
∴∠AEB+∠ADC=90°+(∠ABC+∠ACB)=135°,
∴∠DFE=360°﹣135°﹣90°=135°,
∴∠DFB=45°=∠CGE,
∴∠CGE=2∠DFB,
∴∠DFB=∠CGE,故正确.
故答案为:①②③
三.解答题
21.解:∵a,b,c是△ABC的三边的长,
∴a+c>b,a+b>c,a+c>b,
∴a﹣b+c>0,b﹣c﹣a<0,a﹣c+b>0,
∴|a﹣b+c|﹣|b﹣c﹣a|﹣|a﹣c+b|
=a﹣b+c﹣[﹣(b﹣c﹣a)]﹣(a﹣c+b)
=a﹣b+c+b﹣c﹣a﹣a+c﹣b
=c﹣a﹣b.
22.解:(1)当6是腰时,底边=20﹣6×2=8cm,即其它两边是6cm,8cm,此时6+6=12,能构成三角形;
(2)当6是底边时,腰=(20﹣6)÷2=7cm,此时能构成三角形,所以其它两边是7cm、7cm.
因此其它两边长分别为7cm,7cm,
综上所述两边长分别为6cm,8cm或7cm,7cm.
23.解:(1)
4个;
(2)当有n对点时,最少可以画2(n﹣1)个三角形;
(3)2×(2006﹣1)=4010个.
答:当n=2006时,最少可以画4010个三角形.
24.解:(1)图②有3个三角形;图③有5个三角形;图④有7个三角形;…猜测第七个图形中共有13个三角形.
(2)∵图②有3个三角形,3=2×2﹣1;
图③有5个三角形,5=2×3﹣1;
图④有7个三角形,7=2×4﹣1;
∴第n个图形中有(2n﹣1)个三角形.
故答案为3,5,7,13,(2n﹣1).
25.解:∵CF、BE分别是AB、AC边上的中线,AE=2,AF=3,
∴AB=2AF=2×3=6,
AC=2AE=2×2=4,
∵△ABC的周长为15,
∴BC=15﹣6﹣4=5.
26.解:(1)∵AF是△ABC的中线,
∴BC=2BF=2CF,BF=CF,
∴△ABF和△ACF的面积相等,
∵△AFC的面积为10,
∴∠ABF的面积为10,
∵AD=4,
∴=10,
∴BF=5,
∴BC=2BF=10;
(2)∵AD是△ABC的高,
∴∠ADC=90°,
∵∠DAE=20°,
∴∠AED=180°﹣90°﹣20°=70°,
∵∠C=30°,
∴∠CAE=∠AED﹣∠C=40°,
∵AE是△ABC的角平分线,
∴∠BAC=2∠CAE=80°,
∴∠B=180°﹣∠BAC﹣∠C=180°﹣80°﹣30°=70°.
27.解:(1)BO=2OD,理由如下:
连接DE,
∵BD、CE是边AC、AB上的中线,
∴DE∥BC,DE=BC.
∴△ODE~△OBC,
∴=,
即BO=2OD.
(2)BC边上的中线一定过点O,
理由是:作BC边上的中线AF,交BD于M,
连接DF,
∵BD、AF是边AC、BC上的中线,
.∴DF∥BA,DF=BA.
∴△MDF~△MBA
∴===,
即BD=3DM,
BO=BD,
∴O和M重合,
即BC边上的中线一定过点O.
三角形》单元测试卷
一.选择题
1.下列说法正确的是( )
A.一个钝角三角形一定不是等腰三角形,也不是等边三角形
B.一个等腰三角形一定是锐角三角形,或直角三角形
C.一个直角三角形一定不是等腰三角形,也不是等边三角形
D.一个等边三角形一定不是钝角三角形,也不是直角三角形
2.在下列各图的△ABC中,正确画出AC边上的高的图形是( )
A.
B.
C.
D.
3.如图,AD是△ABC的中线,DE是△ADC的高线,AB=3,AC=5,DE=2,那么点D到AB的距离是( )
A.
B.
C.
D.2
4.在下列四组线段中,能组成三角形的是( )
A.2,2,5
B.3,7,10
C.3,5,9
D.4,5,7
5.如图所示,在△ABC中,∠ACB是钝角,让点C在射线BD上向右移动,则( )
A.△ABC将先变成直角三角形,然后再变成锐角三角形,而不会再是钝角三角形
B.△ABC将变成锐角三角形,而不会再是钝角三角形
C.△ABC将先变成直角三角形,然后再变成锐角三角形,接着又由锐角三角形变为钝角三角形
D.△ABC先由钝角三角形变为直角三角形,再变为锐角三角形,接着又变为直角三角形,然后再次变为钝角三角形
6.三角形三条中线的交点叫做三角形的( )
A.内心
B.外心
C.中心
D.重心
7.如图,△BEF的内角∠EBF平分线BD与外角∠AEF的平分线交于点D,过D作DH∥BC分别交EF、EB于G、H两点.下列结论:①S△EBD:S△FBD=BE:BF;②∠EFD=∠CFD;③HD=HF;④BH﹣GF=HG,其中正确的结论有( )
A.只有①②③
B.只有①②④
C.只有③④
D.①②③④
8.给出下列说法:(1)等边三角形是等腰三角形;(2)三角形按边的相等关系分类可分为等腰三角形、等边三角形和不等边三角形;(3)三角形按角的大小分类可分为锐角三角形、直角三角形和钝角三角形.其中,正确的有( )个.
A.1
B.2
C.3
D.0
9.如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;
②∠AEF=∠AFE;
③∠EBC=∠C;④AG⊥EF.正确结论有( )
A.1个
B.2个
C.3个
D.4个
10.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
①△ABE的面积=△BCE的面积;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.
A.①②③④
B.①②③
C.②④
D.①③
二.填空题
11.如图,长方形ABCD中,AB=4cm,BC=3cm,点E是CD的中点,动点P从A点出发,以每秒1cm的速度沿A→B→C→E运动,最终到达点E.若点P运动的时间为x秒,那么当x=
时,△APE的面积等于5.
12.在Rt△ABC中,AD是斜边BC边上的中线,G是△ABC重心,如果BC=6,那么线段AG的长为
.
13.如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是
.
14.直角三角形两锐角的平分线的夹角是
.
15.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有
对.
16.如图,共有
个三角形.
17.一个三角形的周长为81cm,三边长的比为2:3:4,则最长边比最短边长
.
18.如图,BD是△ABC的中线,AB=8,BC=6,△ABD和△BCD的周长的差是
.
19.三角形的三边长分别为3、7、a,且a为偶数,则这个三角形的周长为
.
20.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠DFB=∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的结论是
.
三.解答题
21.已知a、b、c为三角形的三边长,化简:|a﹣b+c|﹣|b﹣c﹣a|﹣|a﹣c+b|.
22.一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
23.两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为
个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?
24.观察以下图形,回答问题:
(1)图②有
个三角形;图③有
个三角形;图④有
个三角形;…猜测第七个图形中共有
个三角形.
(2)按上面的方法继续下去,第n个图形中有
个三角形(用含n的代数式表示结论).
25.如图,在△ABC中,CF、BE分别是AB、AC边上的中线,若AE=2,AF=3,且△ABC的周长为15,求BC的长.
26.如图,在△ABC中AD、AE、AF分别为△ABC的高、角平分线和中线,已知△AFC的面积为10,AD=4,∠DAE=20°,∠C=30°.
(1)求BC的长度;
(2)求∠B的度数.
27.如图,在△ABC中,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O.
(1)BO与OD的长度有什么关系?并证明你的结论.
(2)BC边上的中线是否一定过点O?为什么?
参考答案与试题解析
一.选择题
1.解:A、一个钝角三角形不一定不是等腰三角形,一定不是等边三角形,故本选项错误;
B、一个等腰三角形不一定是锐角三角形,或直角三角形,故本选项错误;
C、一个直角三角形不一定不是等腰三角形,一定不是等边三角形,故本选项错误;
D、一个等边三角形一定不是钝角三角形,也不是直角三角形,故本选项正确;
故选:D.
2.解:AC边上的高就是过B作垂线垂直AC交AC于某点,因此只有C符合条件,故选C.
3.解:∵AC=5,DE=2,
∴△ADC的面积为=5,
∵AD是△ABC的中线,
∴△ABD的面积为5,
∴点D到AB的距离是.
故选:A.
4.解:A、∵2+2=4<5,
∴2,2,5不能组成三角形,故本选项错误;
B、∵3+7=10,
∴3,7,10不能组成三角形,故本选项错误;
C、∵3+5=8<9,
∴3,5,9不能组成三角形,故本选项错误;
D、4,5,7能组成三角形,故本选项正确.
故选:D.
5.解:根据∠A的旋转变化规律可知:△ABC先由钝角三角形变为直角三角形,再变为锐角三角形,接着又变为直角三角形,然后再次变为钝角三角形.
故选:D.
6.解:三角形的重心是三角形三条中线的交点.
故选:D.
7.解:过D作DM⊥AB,DN⊥CB,DO⊥EF,
①正确.
因为S△EBD=?BE?DM,S△FBD=?BF?DN,
因为BD是∠EBC的平分线,DM⊥AB,DN⊥CB,
所以DM=DN,
所以S△EBD:S△FBD=BE:BF;
②正确.
∵DE是∠AEF的平分线,
∴AD=DO,
∵DB是∠ABC的平分线,
∴DA=DN,
∴DO=DN,
∴DF是∠EFC的平分线,
∴∠EFD=∠CFD;
③错误.
因为HD∥BF,
所以∠HDB=∠FBD,
又因为BD平分∠ABC,
所以∠HBD=∠CBD,
于是∠HBD=∠HDB,
故HB=HD.
但没有条件说明HF与HB必然相等;
④正确.
由于点D为△BEF的内角∠EBF平分线BD与外角∠AEF的平分线的交点,
故D为△BEF的内心,
于是FD为∠EFC的平分线,
故∠CFD=∠EFD,
又因为DH∥BC,
所以∠HDF=∠CFD,
故∠GDF=∠DFE,
于是GF=GD,
又因为HB=HD,
所以HD﹣GD=HG,
即BH﹣GF=HG.
故①②④正确.
故选:B.
8.解:(1)等边三角形是一特殊的等腰三角形,正确;
(2)三角形按边分类可以分为不等边三角形和等腰三角形,错误;
(3)三角形按角分类应分为锐角三角形、直角三角形和钝角三角形,正确.
综上所述,正确的结论2个.
故选:B.
9.解:∵∠BAC=90°,AD⊥BC,
∴∠C+∠ABC=90°,
∠BAD+∠ABC=90°,
∴∠BAD=∠C,故①正确;
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∵∠ABE+∠AEF=90°,
∠CBE+∠BFD=90°,
∴∠AEF=∠BFD,
又∵∠AFE=∠BFD(对顶角相等),
∴∠AEF=∠AFE,故②正确;
∵∠ABE=∠CBE,
∴只有∠C=30°时∠EBC=∠C,故③错误;
∵∠AEF=∠AFE,
∴AE=AF,
∵AG平分∠DAC,
∴AG⊥EF,故④正确.
综上所述,正确的结论是①②④.
故选:C.
10.解:∵BE是中线,
∴AE=CE,
∴△ABE的面积=△BCE的面积(等底等高的三角形的面积相等),故①正确;
∵CF是角平分线,
∴∠ACF=∠BCF,
∵AD为高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,
∴∠ABC=∠CAD,
∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,
∴∠AFG=∠AGF,故②正确;
∵AD为高,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,
∴∠ACB=∠BAD,
∵CF是∠ACB的平分线,
∴∠ACB=2∠ACF,
∴∠BAD=2∠ACF,
即∠FAG=2∠ACF,故③正确;
根据已知条件不能推出∠HBC=∠HCB,即不能推出BH=CH,故④错误;
故选:B.
二.填空题
11.解:①如图1,
当P在AB上时,
∵△APE的面积等于5,
∴x?3=5,
x=;
②当P在BC上时,
∵△APE的面积等于5,
∴S长方形ABCD﹣S△CPE﹣S△ADE﹣S△ABP=5,
∴3×4﹣(3+4﹣x)×2﹣×2×3﹣×4×(x﹣4)=5,
x=5;
③当P在CE上时,
∴(4+3+2﹣x)×3=5,
x=<3+4,此时不符合;
故答案为:或5.
12.解:∵AD是斜边BC边上的中线,
∴AD=BC=×6=3,
∵G是△ABC重心,
∴=2,
∴AG=AD=×3=2.
故答案为2.
13.解:∵∠A=50°,∠C=70°,
∴∠ABD=∠A+∠C=120°,
故答案为:120°.
14.解:如图,∠ABC+∠BAC=90°,
∵AD、BE分别是∠BAC和∠ABC的角平分线,
∴∠OAB+∠OBA=(∠ABC+∠BAC)=45°,
∴∠AOE=∠OAB+∠OBA=45°,
∴∠AOB=135°
∴两锐角的平分线的夹角是45°或135°.
故答案为:45°或135°.
15.解:△BDC与△BEC、△BDC与△BAC、△BEC与△BAC共三对.
故答案为:3.
16.解:上半部分:单个的三角形有3个,复合的三角形有2+1=3个,
所以上半部分三角形的个数为3+3=6个,
同理考虑横截线的三角形的个数也是6个.
故共有12个三角形.
17.解:设三角形的三边长为2x,3x,4x,
由题意得,2x+3x+4x=81,
解得:x=9,
则三角形的三边长分别为:18cm,27cm,36cm,
所以,最长边比最短边长:36﹣18=18(cm).
故答案是:18cm.
18.解:∵BD是△ABC的中线,
∴AD=CD,
∴△ABD和△BCD的周长差=(AB+AD+BD)﹣(BC+CD+BD),
=AB+AD+BD﹣BC﹣CD﹣BD,
=AB﹣BC,
∵AB=8,BC=6,
∴△ABD和△BCD的周长差=8﹣6=2.
答:△ABD和△BCD的周长差为2.
故答案为:2
19.解:∵7﹣3<a<7+3,
∴4<a<10,
又∵第三边是偶数,
∴a的值:6或8;
∴三角形的周长为:3+6+7=16或3+8+7=18.
故答案为:16或18.
20.解:①∵EG∥BC,
∴∠CEG=∠ACB,
又∵CD是△ABC的角平分线,
∴∠CEG=∠ACB=2∠DCB,故正确;
④无法证明CA平分∠BCG,故错误;
③∵∠A=90°,
∴∠ADC+∠ACD=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ADC+∠BCD=90°.
∵EG∥BC,且CG⊥EG,
∴∠GCB=90°,即∠GCD+∠BCD=90°,
∴∠ADC=∠GCD,故正确;
②∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,
∴∠AEB+∠ADC=90°+(∠ABC+∠ACB)=135°,
∴∠DFE=360°﹣135°﹣90°=135°,
∴∠DFB=45°=∠CGE,
∴∠CGE=2∠DFB,
∴∠DFB=∠CGE,故正确.
故答案为:①②③
三.解答题
21.解:∵a,b,c是△ABC的三边的长,
∴a+c>b,a+b>c,a+c>b,
∴a﹣b+c>0,b﹣c﹣a<0,a﹣c+b>0,
∴|a﹣b+c|﹣|b﹣c﹣a|﹣|a﹣c+b|
=a﹣b+c﹣[﹣(b﹣c﹣a)]﹣(a﹣c+b)
=a﹣b+c+b﹣c﹣a﹣a+c﹣b
=c﹣a﹣b.
22.解:(1)当6是腰时,底边=20﹣6×2=8cm,即其它两边是6cm,8cm,此时6+6=12,能构成三角形;
(2)当6是底边时,腰=(20﹣6)÷2=7cm,此时能构成三角形,所以其它两边是7cm、7cm.
因此其它两边长分别为7cm,7cm,
综上所述两边长分别为6cm,8cm或7cm,7cm.
23.解:(1)
4个;
(2)当有n对点时,最少可以画2(n﹣1)个三角形;
(3)2×(2006﹣1)=4010个.
答:当n=2006时,最少可以画4010个三角形.
24.解:(1)图②有3个三角形;图③有5个三角形;图④有7个三角形;…猜测第七个图形中共有13个三角形.
(2)∵图②有3个三角形,3=2×2﹣1;
图③有5个三角形,5=2×3﹣1;
图④有7个三角形,7=2×4﹣1;
∴第n个图形中有(2n﹣1)个三角形.
故答案为3,5,7,13,(2n﹣1).
25.解:∵CF、BE分别是AB、AC边上的中线,AE=2,AF=3,
∴AB=2AF=2×3=6,
AC=2AE=2×2=4,
∵△ABC的周长为15,
∴BC=15﹣6﹣4=5.
26.解:(1)∵AF是△ABC的中线,
∴BC=2BF=2CF,BF=CF,
∴△ABF和△ACF的面积相等,
∵△AFC的面积为10,
∴∠ABF的面积为10,
∵AD=4,
∴=10,
∴BF=5,
∴BC=2BF=10;
(2)∵AD是△ABC的高,
∴∠ADC=90°,
∵∠DAE=20°,
∴∠AED=180°﹣90°﹣20°=70°,
∵∠C=30°,
∴∠CAE=∠AED﹣∠C=40°,
∵AE是△ABC的角平分线,
∴∠BAC=2∠CAE=80°,
∴∠B=180°﹣∠BAC﹣∠C=180°﹣80°﹣30°=70°.
27.解:(1)BO=2OD,理由如下:
连接DE,
∵BD、CE是边AC、AB上的中线,
∴DE∥BC,DE=BC.
∴△ODE~△OBC,
∴=,
即BO=2OD.
(2)BC边上的中线一定过点O,
理由是:作BC边上的中线AF,交BD于M,
连接DF,
∵BD、AF是边AC、BC上的中线,
.∴DF∥BA,DF=BA.
∴△MDF~△MBA
∴===,
即BD=3DM,
BO=BD,
∴O和M重合,
即BC边上的中线一定过点O.
