《导数的应用》教学设计-湘教版数学选修1-1
文档属性
| 名称 | 《导数的应用》教学设计-湘教版数学选修1-1 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 00:00:00 | ||
图片预览



文档简介
《导数的应用》教学设计
【教学目标】
1.理解函数的单调性和导数的关系,会用导数求函数的单调区间、极值和最值进而解决函数的零点及不等式问题,从而在导数综合应用中,形成一定的方法;
2.培养学生的数形结合、函数与方程、转化等数学思想,并侧重体会导数应用中的数形结合思想.
【学情分析】导数的应用是高考考查的热点、重点和难点,题型既有灵活多变的客观性试题,又有具有一定能力要求的主观性试题,作为文科生有一定的畏难情绪,在对导数的概念和导数的几何意义的理解上尚不够深入,在利用导数研究函数的性质并作出函数图象存在一定的困难,树立利用导数处理问题的意识较为淡薄;在利用导数研究函数零点问题中的转化能力有待加强。
【教学重点】能利用导数研究函数的单调性,会求函数的单调区间、极值和最值,会用导数研究函数的零点问题.
【教学难点】利用导数研究函数的零点和不等式恒成立问题.
【知识回顾】
1.导数与函数的单调性的关系
2.利用导数求函数极值、最值的一般步骤:
(1)求函数y=fx的极值的步骤:
第一步:求定义域;
第二步:求导数f'x;
第三步:求驻点,即求方程f'x=0的根x0;
第四步:检查f'x在x=x0左右的符号;
①左正右负?fx在x=x0处取得极大值;
②左负右正?fx在x=x0处取得极小值.
(2)求函数y=fx在区间[a,b]上的最大值与最小值的步骤:
第一步:求函数y=fx在区间(a,b)内的极值;
第二步:将y=fx的所有极值与端点处的函数值fa、fb进行比较,其中最大的一个为最大值,最小的一个为最小值.
【典例剖析】
一、利用导数判定函数图象
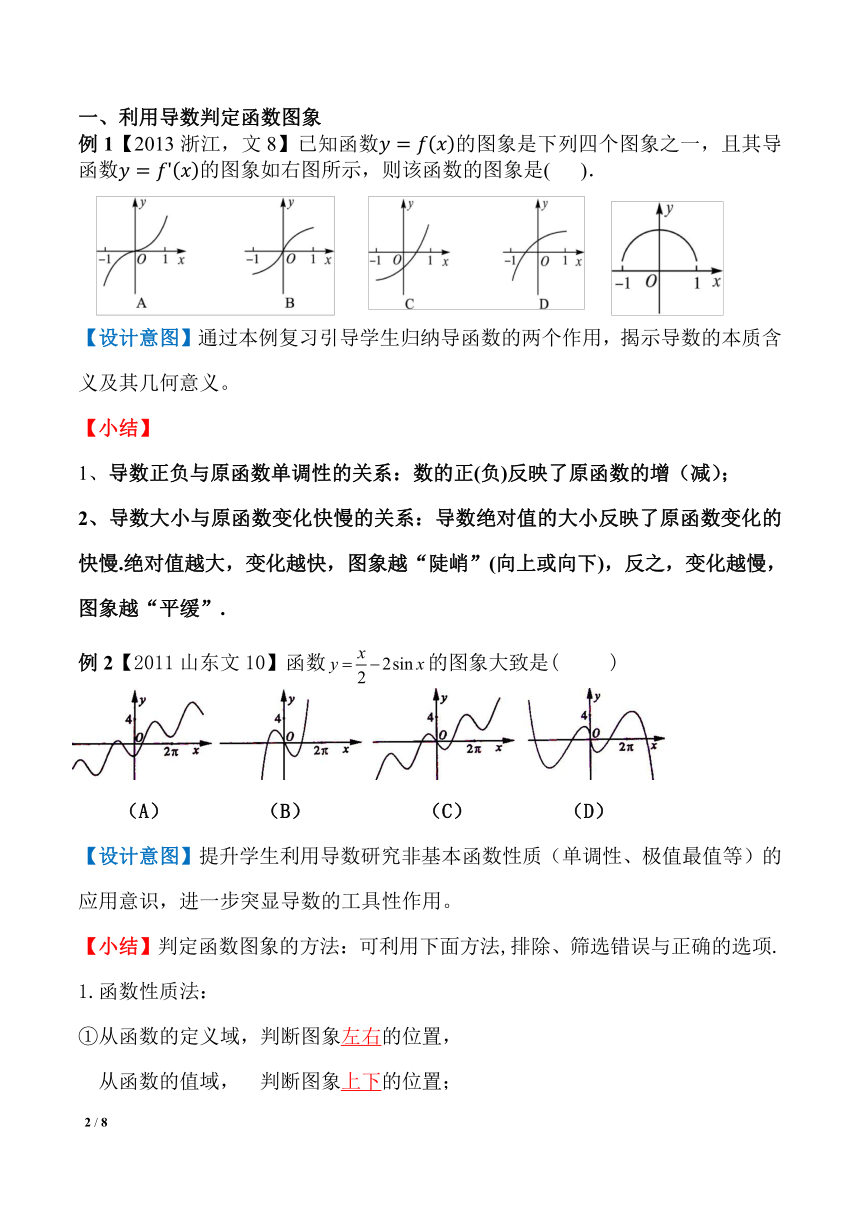
例1【2013浙江,文8】已知函数y=fx的图象是下列四个图象之一,且其导函数y=f'x的图象如右图所示,则该函数的图象是( ).
46958251714501619251231902552700123190
【设计意图】通过本例复习引导学生归纳导函数的两个作用,揭示导数的本质含义及其几何意义。
【小结】
1、导数正负与原函数单调性的关系:数的正(负)反映了原函数的增(减);
2、导数大小与原函数变化快慢的关系:导数绝对值的大小反映了原函数变化的快慢.绝对值越大,变化越快,图象越“陡峭”(向上或向下),反之,变化越慢,图象越“平缓”.
例2【2011山东文10】-48895514350函数false的图象大致是( )
(A) (B) (C) (D)
【设计意图】提升学生利用导数研究非基本函数性质(单调性、极值最值等)的应用意识,进一步突显导数的工具性作用。
【小结】判定函数图象的方法:可利用下面方法,排除、筛选错误与正确的选项.
1.函数性质法:
①从函数的定义域,判断图象左右的位置,
从函数的值域, 判断图象上下的位置;
②从函数的奇偶性,判断图象的对称性;
③从函数的单调性,判断图象的趋势;(可借助导数)
④从函数的周期性,判断图象的往复循环;
⑤从函数的极值点,判断图象的拐点;(可借助导数)
⑥从函数的零点, 判断图象与X轴的交点;
2.特殊值检验法:代入特殊值检验。
二、利用导数研究函数零点问题
例3已知函数fx= ex-ax 有零点,求实数a的取值范围.
【设计意图】提升学生的转化能力;一题多解,提升思维的广度,注重思想、方法的训练与归纳提升。
【解析1】分类讨论法:
①a=0,fx= ex>0,fx没有零点,
②若a<0, f'x= ex-a>0, fx在R上单调递增,
又f0=1>0,f1a=e1a-a?1a=e1a-1<0∴f0?f1a<0,所以根据零点存在性定理及单调性知fx在R上存在唯一零点.
③若a>0,令 f'x= ex-a=0 得x=lna.
当x变化时,f'x, fx的变化情况如下表:
x
(-∞,lna)
lna
(lna,+∞)
f'x
-
0
+
fx
↘
a-alna
↗
∴fx在取得唯一极小值也即最小值flna=a-alna,
又当x→-∞, fx→+∞,
则fx要有零点,则必须且只需a-alna≤0,又a>0,解得a≥e
综上①②③,得a<0或a≥e
【解析2】分离参数法:
函数fx= ex-ax 有零点即方程 ex=ax有解,即方程 a=exx(x≠0)有解,即y=a的图象与y=exx(x≠0)图象有交点.
令gx=exx (x≠0) , g'(x)= ex(x-1)x2
当x变化时,g'x, gx的变化情况如下表:
x
(-∞,0)
0
(0,1)
1
(1,+∞)
g'x
-
不存在
-
0
+
gx
↘
不存在
↘
极小值e
↗
又当x→-∞, gx→0,且x<0时,gx<0
得gx的大致图象如下:013335
如图可知当a≥e或a<0时,两个函数图象有交点,
即函数fx= ex-ax 有零点 .
【解析3】分离函数法:
4362450319405函数fx= ex-ax 有零点等价于函数y= ex的图象与函数y=ax图象有交点. 设y=ax与y= ex相切于(x?,y?)
则有a=ex?ax?=ex?解得x?=1a=e,
如图,当a<0或a=e时,y= ex与y=ax
图象有一个交点,当a>e时图象有两个交点,
当0≤a综上,当a≥e或a<0时,两个函数图象有交点即函数fx= ex-ax 有零点.
【思考】将“有零点”改为“有两个零点”,则实数a的取值范围为 .
【小结】利用导数研究函数零点的破解策略
重要类型
破解策略
应用函数零点、图象交点及方程解的存在情况,求参数的值或取值范围问题
false
【知识点链接】函数零点的相关知识:
1933575611505a定义:对于函数y=fx,把使 的实数x叫做函数y=fx的零点.
b三个等价关系:
f(x)与g(x)的图象有交点
f(x)=g(x)有实数根
F(x)=f(x)-g(x)有零点
变形拓展:
c零点存在性定理:
三、利用导数解决不等式恒成立问题
例4已知不等式 ex-ax>0在0,+∞上恒成立,求实数a的取值范围.请参考例3分析例4的解题思路。
【设计意图】对例3的拓展变式,注重解题思路方法的迁移与延伸,从而实现高效复习。
【思路分析】
思路一:变形为 ex>ax,转化为当x∈(0,+∞)时,函数y= ex图象恒在直线
y=ax的上方—数形结合法
思路二:变形为a思路三:构造函数fx= ex-ax(x>0),转化为求fxmin>0—构造函数法
【小结】利用导数解决不等式的重要类型及破解策略
重要类型
破解策略
恒成立
问题:
false在区间D上恒成立,求参数取值范围
策略一:数形结合法,转化为两个函数false图象与false图
象的上下关系,数形结合求解.
策略二:分离参数法,将不等式变成形如:“false恒成立”或
“false恒成立”,再利用导数求false在D上的最值,
①false,
②false.
策略三:构造函数法,构造函数false,再利用导数
求函数false在区间D上的最小值,
即false
【总结归纳】
1、知识与方法:
①利用导数判定函数的图象的常见策略:
导函数法、函数性质法、特值检验法
②利用导数根据函数零点存在情况求参数范围的常见策略:
直接法、分离参数法、分离函数法、分类讨论法
③利用导数解决不等式恒成立的常见策略:
数形结合法、分离参数法、构造函数法
2数学思想:
数形结合 、函数与方程、分类讨论、化归与转化等
482917593345【课后练习】
1如图,半径为1的圆M,切直线AB于点O,射线OC从OA出发,绕O点顺时针方向旋转到OB,旋转过程中OC交⊙M于P,记∠PMO为x,弓形PNO的面积S=f(x),那么f(x)的大致图象() A.B.C.D.
4828540628652【2015安徽,文10】函数false的图像 如图所示,则下列结论成立的是( )
A. a>0,b<0,c>0,d>0 B.a>0,b<0,c<0,d>0
C .a<0,b<0,c<0,d>0 D a>0,b>0,c>0,d<0
3【2013新课标1文9】函数false在false的图像大致为( )
4若函数f(x)=|lnx|-ax在区间(0,3]上有三个零点,则实数a的取值范围是( )
A.0,1e B.ln33,e C.0,ln33 D.[ln33,1e)
5【2013安徽文10】已知函数false有两个极值点false,若false,则关于false的方程false的不同实根个数为( )
A .3 B. 4 C. 5 D. 6
6 【2014新课标1文12】已知函数false=false,若false存在唯一的零点false,且false>0,则false的取值范围为( )
false.(2,+∞) false.(-∞,-2) false.(1,+∞) false.(-∞,-1)
7【2013新课标Ⅰ文12】)已知函数false,若false,则false的
取值范围是( )
A.false B.false C.false D.false
8【2013福建文22】已知函数fx=x-1+1 ex ,若直线l:y=kx-1与曲线
y=f(x)没有公共点,求k的最大值.
【教学目标】
1.理解函数的单调性和导数的关系,会用导数求函数的单调区间、极值和最值进而解决函数的零点及不等式问题,从而在导数综合应用中,形成一定的方法;
2.培养学生的数形结合、函数与方程、转化等数学思想,并侧重体会导数应用中的数形结合思想.
【学情分析】导数的应用是高考考查的热点、重点和难点,题型既有灵活多变的客观性试题,又有具有一定能力要求的主观性试题,作为文科生有一定的畏难情绪,在对导数的概念和导数的几何意义的理解上尚不够深入,在利用导数研究函数的性质并作出函数图象存在一定的困难,树立利用导数处理问题的意识较为淡薄;在利用导数研究函数零点问题中的转化能力有待加强。
【教学重点】能利用导数研究函数的单调性,会求函数的单调区间、极值和最值,会用导数研究函数的零点问题.
【教学难点】利用导数研究函数的零点和不等式恒成立问题.
【知识回顾】
1.导数与函数的单调性的关系
2.利用导数求函数极值、最值的一般步骤:
(1)求函数y=fx的极值的步骤:
第一步:求定义域;
第二步:求导数f'x;
第三步:求驻点,即求方程f'x=0的根x0;
第四步:检查f'x在x=x0左右的符号;
①左正右负?fx在x=x0处取得极大值;
②左负右正?fx在x=x0处取得极小值.
(2)求函数y=fx在区间[a,b]上的最大值与最小值的步骤:
第一步:求函数y=fx在区间(a,b)内的极值;
第二步:将y=fx的所有极值与端点处的函数值fa、fb进行比较,其中最大的一个为最大值,最小的一个为最小值.
【典例剖析】
一、利用导数判定函数图象
例1【2013浙江,文8】已知函数y=fx的图象是下列四个图象之一,且其导函数y=f'x的图象如右图所示,则该函数的图象是( ).
46958251714501619251231902552700123190
【设计意图】通过本例复习引导学生归纳导函数的两个作用,揭示导数的本质含义及其几何意义。
【小结】
1、导数正负与原函数单调性的关系:数的正(负)反映了原函数的增(减);
2、导数大小与原函数变化快慢的关系:导数绝对值的大小反映了原函数变化的快慢.绝对值越大,变化越快,图象越“陡峭”(向上或向下),反之,变化越慢,图象越“平缓”.
例2【2011山东文10】-48895514350函数false的图象大致是( )
(A) (B) (C) (D)
【设计意图】提升学生利用导数研究非基本函数性质(单调性、极值最值等)的应用意识,进一步突显导数的工具性作用。
【小结】判定函数图象的方法:可利用下面方法,排除、筛选错误与正确的选项.
1.函数性质法:
①从函数的定义域,判断图象左右的位置,
从函数的值域, 判断图象上下的位置;
②从函数的奇偶性,判断图象的对称性;
③从函数的单调性,判断图象的趋势;(可借助导数)
④从函数的周期性,判断图象的往复循环;
⑤从函数的极值点,判断图象的拐点;(可借助导数)
⑥从函数的零点, 判断图象与X轴的交点;
2.特殊值检验法:代入特殊值检验。
二、利用导数研究函数零点问题
例3已知函数fx= ex-ax 有零点,求实数a的取值范围.
【设计意图】提升学生的转化能力;一题多解,提升思维的广度,注重思想、方法的训练与归纳提升。
【解析1】分类讨论法:
①a=0,fx= ex>0,fx没有零点,
②若a<0, f'x= ex-a>0, fx在R上单调递增,
又f0=1>0,f1a=e1a-a?1a=e1a-1<0∴f0?f1a<0,所以根据零点存在性定理及单调性知fx在R上存在唯一零点.
③若a>0,令 f'x= ex-a=0 得x=lna.
当x变化时,f'x, fx的变化情况如下表:
x
(-∞,lna)
lna
(lna,+∞)
f'x
-
0
+
fx
↘
a-alna
↗
∴fx在取得唯一极小值也即最小值flna=a-alna,
又当x→-∞, fx→+∞,
则fx要有零点,则必须且只需a-alna≤0,又a>0,解得a≥e
综上①②③,得a<0或a≥e
【解析2】分离参数法:
函数fx= ex-ax 有零点即方程 ex=ax有解,即方程 a=exx(x≠0)有解,即y=a的图象与y=exx(x≠0)图象有交点.
令gx=exx (x≠0) , g'(x)= ex(x-1)x2
当x变化时,g'x, gx的变化情况如下表:
x
(-∞,0)
0
(0,1)
1
(1,+∞)
g'x
-
不存在
-
0
+
gx
↘
不存在
↘
极小值e
↗
又当x→-∞, gx→0,且x<0时,gx<0
得gx的大致图象如下:013335
如图可知当a≥e或a<0时,两个函数图象有交点,
即函数fx= ex-ax 有零点 .
【解析3】分离函数法:
4362450319405函数fx= ex-ax 有零点等价于函数y= ex的图象与函数y=ax图象有交点. 设y=ax与y= ex相切于(x?,y?)
则有a=ex?ax?=ex?解得x?=1a=e,
如图,当a<0或a=e时,y= ex与y=ax
图象有一个交点,当a>e时图象有两个交点,
当0≤a
【思考】将“有零点”改为“有两个零点”,则实数a的取值范围为 .
【小结】利用导数研究函数零点的破解策略
重要类型
破解策略
应用函数零点、图象交点及方程解的存在情况,求参数的值或取值范围问题
false
【知识点链接】函数零点的相关知识:
1933575611505a定义:对于函数y=fx,把使 的实数x叫做函数y=fx的零点.
b三个等价关系:
f(x)与g(x)的图象有交点
f(x)=g(x)有实数根
F(x)=f(x)-g(x)有零点
变形拓展:
c零点存在性定理:
三、利用导数解决不等式恒成立问题
例4已知不等式 ex-ax>0在0,+∞上恒成立,求实数a的取值范围.请参考例3分析例4的解题思路。
【设计意图】对例3的拓展变式,注重解题思路方法的迁移与延伸,从而实现高效复习。
【思路分析】
思路一:变形为 ex>ax,转化为当x∈(0,+∞)时,函数y= ex图象恒在直线
y=ax的上方—数形结合法
思路二:变形为a
【小结】利用导数解决不等式的重要类型及破解策略
重要类型
破解策略
恒成立
问题:
false在区间D上恒成立,求参数取值范围
策略一:数形结合法,转化为两个函数false图象与false图
象的上下关系,数形结合求解.
策略二:分离参数法,将不等式变成形如:“false恒成立”或
“false恒成立”,再利用导数求false在D上的最值,
①false,
②false.
策略三:构造函数法,构造函数false,再利用导数
求函数false在区间D上的最小值,
即false
【总结归纳】
1、知识与方法:
①利用导数判定函数的图象的常见策略:
导函数法、函数性质法、特值检验法
②利用导数根据函数零点存在情况求参数范围的常见策略:
直接法、分离参数法、分离函数法、分类讨论法
③利用导数解决不等式恒成立的常见策略:
数形结合法、分离参数法、构造函数法
2数学思想:
数形结合 、函数与方程、分类讨论、化归与转化等
482917593345【课后练习】
1如图,半径为1的圆M,切直线AB于点O,射线OC从OA出发,绕O点顺时针方向旋转到OB,旋转过程中OC交⊙M于P,记∠PMO为x,弓形PNO的面积S=f(x),那么f(x)的大致图象() A.B.C.D.
4828540628652【2015安徽,文10】函数false的图像 如图所示,则下列结论成立的是( )
A. a>0,b<0,c>0,d>0 B.a>0,b<0,c<0,d>0
C .a<0,b<0,c<0,d>0 D a>0,b>0,c>0,d<0
3【2013新课标1文9】函数false在false的图像大致为( )
4若函数f(x)=|lnx|-ax在区间(0,3]上有三个零点,则实数a的取值范围是( )
A.0,1e B.ln33,e C.0,ln33 D.[ln33,1e)
5【2013安徽文10】已知函数false有两个极值点false,若false,则关于false的方程false的不同实根个数为( )
A .3 B. 4 C. 5 D. 6
6 【2014新课标1文12】已知函数false=false,若false存在唯一的零点false,且false>0,则false的取值范围为( )
false.(2,+∞) false.(-∞,-2) false.(1,+∞) false.(-∞,-1)
7【2013新课标Ⅰ文12】)已知函数false,若false,则false的
取值范围是( )
A.false B.false C.false D.false
8【2013福建文22】已知函数fx=x-1+1 ex ,若直线l:y=kx-1与曲线
y=f(x)没有公共点,求k的最大值.
同课章节目录
