2.2.2双曲线的简单几何性质(1)课件-湘教版数学选修1-1
文档属性
| 名称 | 2.2.2双曲线的简单几何性质(1)课件-湘教版数学选修1-1 |  | |
| 格式 | pptx | ||
| 文件大小 | 656.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 21:16:37 | ||
图片预览




文档简介
2.2.2双曲线的简单几何性质
o
Y
X
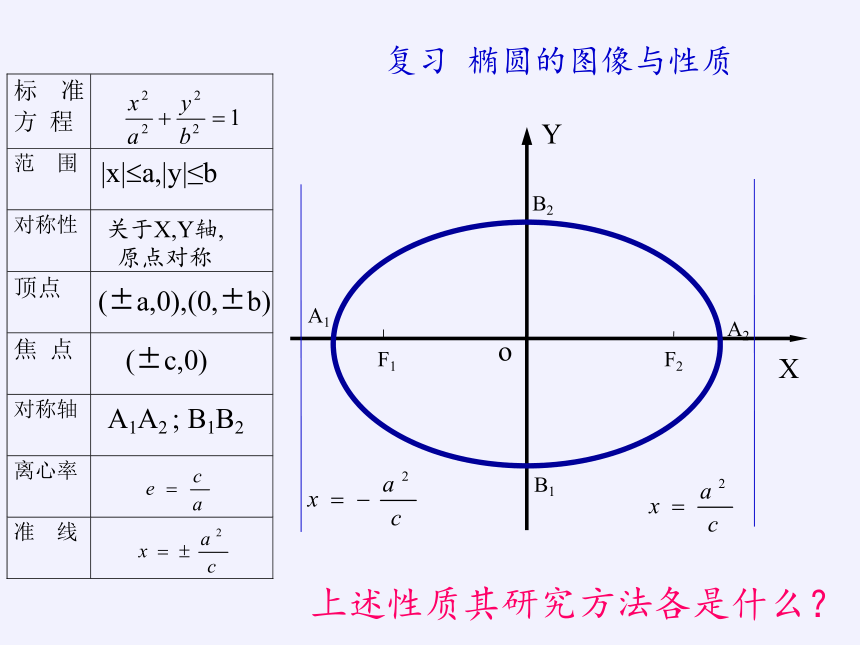
关于X,Y轴,
原点对称
(±a,0),(0,±b)
(±c,0)
A1A2 ; B1B2
|x|?a,|y|≤b
F1
F2
A1
A2
B2
B1
复习 椭圆的图像与性质
上述性质其研究方法各是什么?
双曲线的标准方程
形式一:
(焦点在x轴上,(-c,0)、 (c,0))
形式二:
(焦点在y轴上,(0,-c)、(0,c))
其中
复 习
Y
X
F1
F2
A1
A2
B1
B2
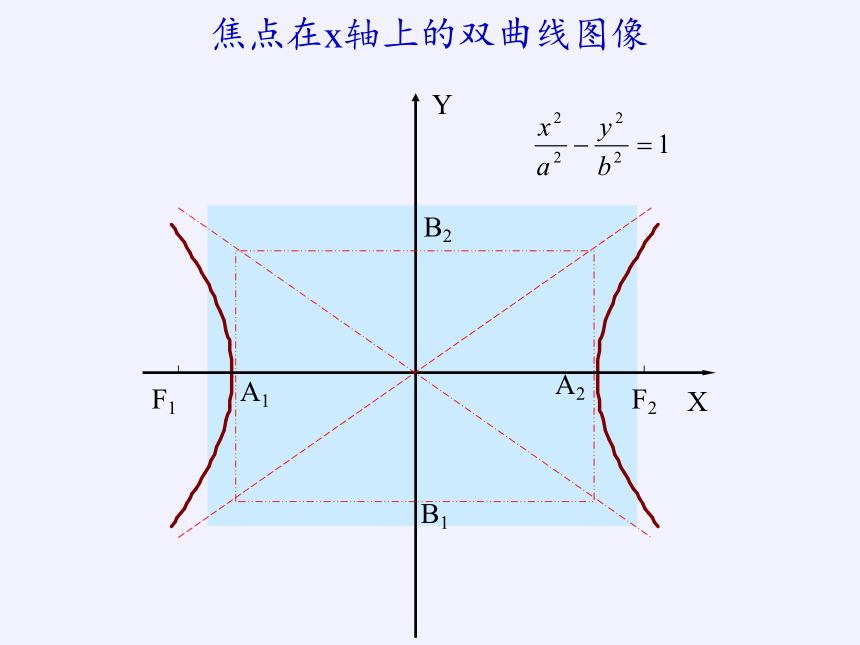
焦点在x轴上的双曲线图像
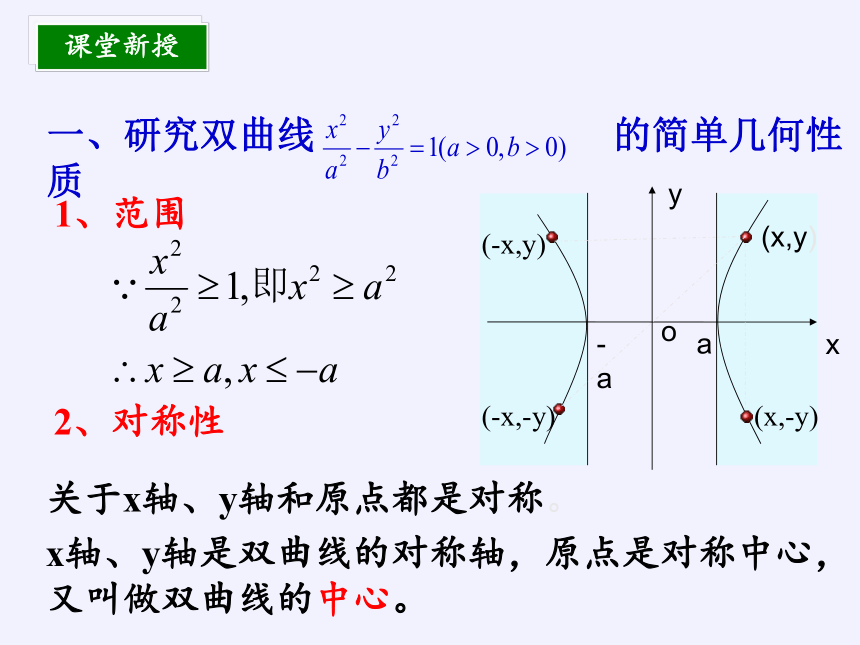
2、对称性
一、研究双曲线 的简单几何性质
1、范围
关于x轴、y轴和原点都是对称。
x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。
x
y
o
-a
a
(-x,-y)
(-x,y)
(x,y)
(x,-y)
课堂新授
3、顶点
(1)双曲线与对称轴的交点,叫做双曲线的顶点
x
y
o
-b
b
-a
a
如图,线段 叫做双曲线的实轴,它的长为2a,a叫做实半轴长;线段 叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长
(2)
实轴与虚轴等长的双曲线
叫等轴双曲线
(3)
M(x,y)
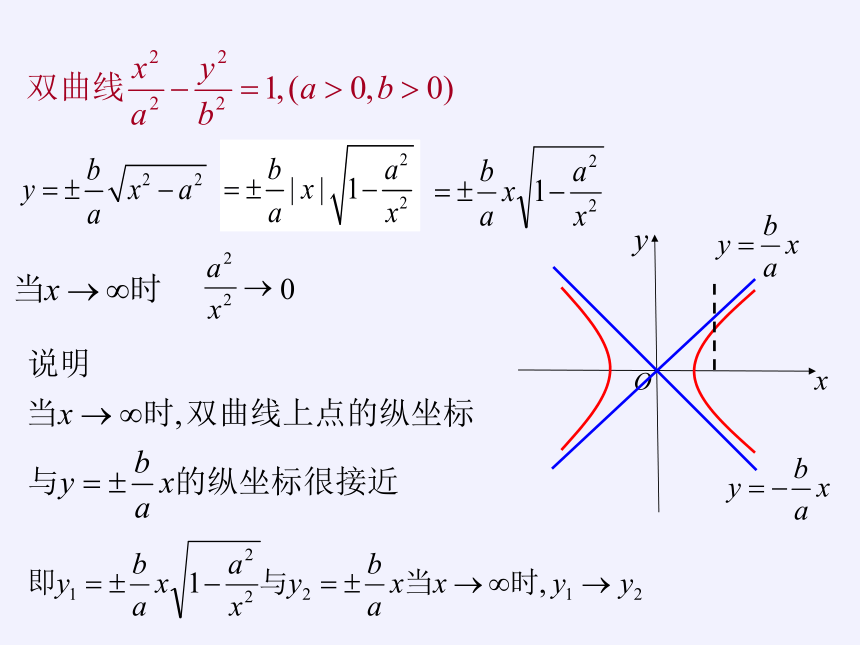
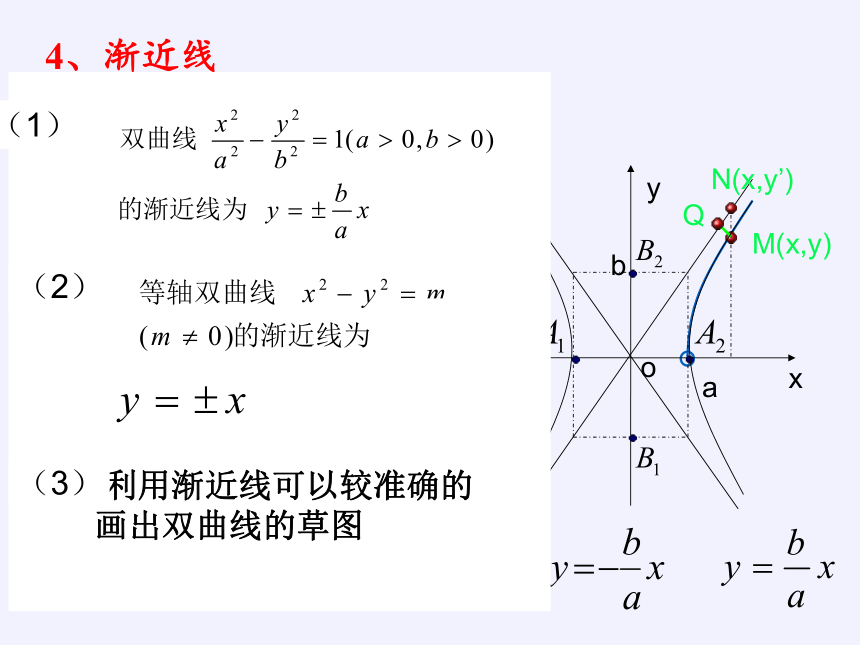
4、渐近线
N(x,y’)
Q
慢慢靠近
x
y
o
a
b
(1)
(2)
利用渐近线可以较准确的
画出双曲线的草图
(3)
5、离心率
离心率。
c>a>0
e >1
e是表示双曲线开口大小的一个量,e越大开口越大
(1)定义:
(2)e的范围:
(3)e的含义:
(4)等轴双曲线的离心率e= ?
( 5 )
A1
A2
B1
B2
a
b
c
x
0
y
几何意义
X
Y
F1
F2
O
B1
B2
A2
A1
焦点在y轴上的双曲线图像
焦点在y轴上的双曲线的几何性质口答
双曲线标准方程:
Y
X
双曲线性质:
1、
范围:
y≥a或y≤-a
2、对称性:
关于x轴,y轴,原点对称。
3、顶点
B1(0,-a),B2(0,a)
4、轴:实轴 B1B2 ; 虚轴 A1A2
A1
A2
B1
B2
5、渐近线方程:
6、离心率:
e=c/a
F2
F2
o
如何记忆双曲线的渐进线方程?
小 结
x
y
o
或
或
关于坐标
轴和
原点
都对
称
性质
双曲线
范围
对称
性
顶点
渐近
线
离心
率
图象
x
y
o
1、练习
|x|≥
6
18
|x|≥3
(±3,0)
y=±3x
4
4
|y|≥2
(0,±2)
10
14
|y|≥5
(0,±5)
例1 :求双曲线
的实半轴长,虚半轴长,
焦点坐标,离心率.渐近线方程。
解:把方程化为标准方程
可得:实半轴长a=4
虚半轴长b=3
半焦距c=
焦点坐标是(0,-5),(0,5)
离心率:
渐近线方程:
144
16
9
2
2
=
-
x
y
1
3
4
2
2
2
2
=
-
x
y
5
3
4
2
2
=
+
4
5
=
=
a
c
e
例题讲解
P54,A 3,4,B,1
小结:
本节课讨论了双曲线的简单几何性质:范围,对称性,顶点,离心率,渐近线,请同学们熟练掌握。
作业
1
2
=
+
b
y
a
x
2
2
2
( a> b >0)
1
2
2
2
2
=
-
b
y
a
x
( a> 0 b>0)
2
2
2
=
+
b
a
(a> 0 b>0)
c
2
2
2
=
-
b
a
(a> b>0)
c
椭 圆
双曲线
方程
a b c关系
图象
椭圆与双曲线的性质比较
y
X
F1
0
F2
M
X
Y
0
F1
F2
p
小 结
渐近线
离心率
顶点
对称性
范围
准线
|x|?a,|y|≤b
|x| ≥ a,y?R
对称轴:x轴,y轴
对称中心:原点
对称轴:x轴,y轴
对称中心:原点
(-a,0) (a,0)
(0,b) (0,-b)
长轴:2a 短轴:2b
(-a,0) (a,0)
实轴:2a
虚轴:2b
e =
a
c
( 0<e <1 )
a
c
e=
(e?1)
无
y =
a
b
x
±
谢谢光临!
证明:(1)设已知双曲线的方程是:
则它的共轭双曲线方程是:
渐近线为:
渐近线为:
可化为:
故双曲线和它的共轭双曲线有共同的渐近线
(2)设已知双曲线的焦点为F(c,0),F(-c,0)
它的共轭双曲线的焦点为F1(0,c), F2(0,-c),
∵
∴c=c'
所以四个焦点F1, F2, F3, F4在同一个圆
问:有相同渐近线的双曲线方程一定是共轭双曲线吗?
谢 谢
o
Y
X
关于X,Y轴,
原点对称
(±a,0),(0,±b)
(±c,0)
A1A2 ; B1B2
|x|?a,|y|≤b
F1
F2
A1
A2
B2
B1
复习 椭圆的图像与性质
上述性质其研究方法各是什么?
双曲线的标准方程
形式一:
(焦点在x轴上,(-c,0)、 (c,0))
形式二:
(焦点在y轴上,(0,-c)、(0,c))
其中
复 习
Y
X
F1
F2
A1
A2
B1
B2
焦点在x轴上的双曲线图像
2、对称性
一、研究双曲线 的简单几何性质
1、范围
关于x轴、y轴和原点都是对称。
x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。
x
y
o
-a
a
(-x,-y)
(-x,y)
(x,y)
(x,-y)
课堂新授
3、顶点
(1)双曲线与对称轴的交点,叫做双曲线的顶点
x
y
o
-b
b
-a
a
如图,线段 叫做双曲线的实轴,它的长为2a,a叫做实半轴长;线段 叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长
(2)
实轴与虚轴等长的双曲线
叫等轴双曲线
(3)
M(x,y)
4、渐近线
N(x,y’)
Q
慢慢靠近
x
y
o
a
b
(1)
(2)
利用渐近线可以较准确的
画出双曲线的草图
(3)
5、离心率
离心率。
c>a>0
e >1
e是表示双曲线开口大小的一个量,e越大开口越大
(1)定义:
(2)e的范围:
(3)e的含义:
(4)等轴双曲线的离心率e= ?
( 5 )
A1
A2
B1
B2
a
b
c
x
0
y
几何意义
X
Y
F1
F2
O
B1
B2
A2
A1
焦点在y轴上的双曲线图像
焦点在y轴上的双曲线的几何性质口答
双曲线标准方程:
Y
X
双曲线性质:
1、
范围:
y≥a或y≤-a
2、对称性:
关于x轴,y轴,原点对称。
3、顶点
B1(0,-a),B2(0,a)
4、轴:实轴 B1B2 ; 虚轴 A1A2
A1
A2
B1
B2
5、渐近线方程:
6、离心率:
e=c/a
F2
F2
o
如何记忆双曲线的渐进线方程?
小 结
x
y
o
或
或
关于坐标
轴和
原点
都对
称
性质
双曲线
范围
对称
性
顶点
渐近
线
离心
率
图象
x
y
o
1、练习
|x|≥
6
18
|x|≥3
(±3,0)
y=±3x
4
4
|y|≥2
(0,±2)
10
14
|y|≥5
(0,±5)
例1 :求双曲线
的实半轴长,虚半轴长,
焦点坐标,离心率.渐近线方程。
解:把方程化为标准方程
可得:实半轴长a=4
虚半轴长b=3
半焦距c=
焦点坐标是(0,-5),(0,5)
离心率:
渐近线方程:
144
16
9
2
2
=
-
x
y
1
3
4
2
2
2
2
=
-
x
y
5
3
4
2
2
=
+
4
5
=
=
a
c
e
例题讲解
P54,A 3,4,B,1
小结:
本节课讨论了双曲线的简单几何性质:范围,对称性,顶点,离心率,渐近线,请同学们熟练掌握。
作业
1
2
=
+
b
y
a
x
2
2
2
( a> b >0)
1
2
2
2
2
=
-
b
y
a
x
( a> 0 b>0)
2
2
2
=
+
b
a
(a> 0 b>0)
c
2
2
2
=
-
b
a
(a> b>0)
c
椭 圆
双曲线
方程
a b c关系
图象
椭圆与双曲线的性质比较
y
X
F1
0
F2
M
X
Y
0
F1
F2
p
小 结
渐近线
离心率
顶点
对称性
范围
准线
|x|?a,|y|≤b
|x| ≥ a,y?R
对称轴:x轴,y轴
对称中心:原点
对称轴:x轴,y轴
对称中心:原点
(-a,0) (a,0)
(0,b) (0,-b)
长轴:2a 短轴:2b
(-a,0) (a,0)
实轴:2a
虚轴:2b
e =
a
c
( 0<e <1 )
a
c
e=
(e?1)
无
y =
a
b
x
±
谢谢光临!
证明:(1)设已知双曲线的方程是:
则它的共轭双曲线方程是:
渐近线为:
渐近线为:
可化为:
故双曲线和它的共轭双曲线有共同的渐近线
(2)设已知双曲线的焦点为F(c,0),F(-c,0)
它的共轭双曲线的焦点为F1(0,c), F2(0,-c),
∵
∴c=c'
所以四个焦点F1, F2, F3, F4在同一个圆
问:有相同渐近线的双曲线方程一定是共轭双曲线吗?
谢 谢
同课章节目录
