3.2.3导数的运算法则_课件1(1)-湘教版数学选修1-1(30张PPT)
文档属性
| 名称 | 3.2.3导数的运算法则_课件1(1)-湘教版数学选修1-1(30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 21:35:56 | ||
图片预览




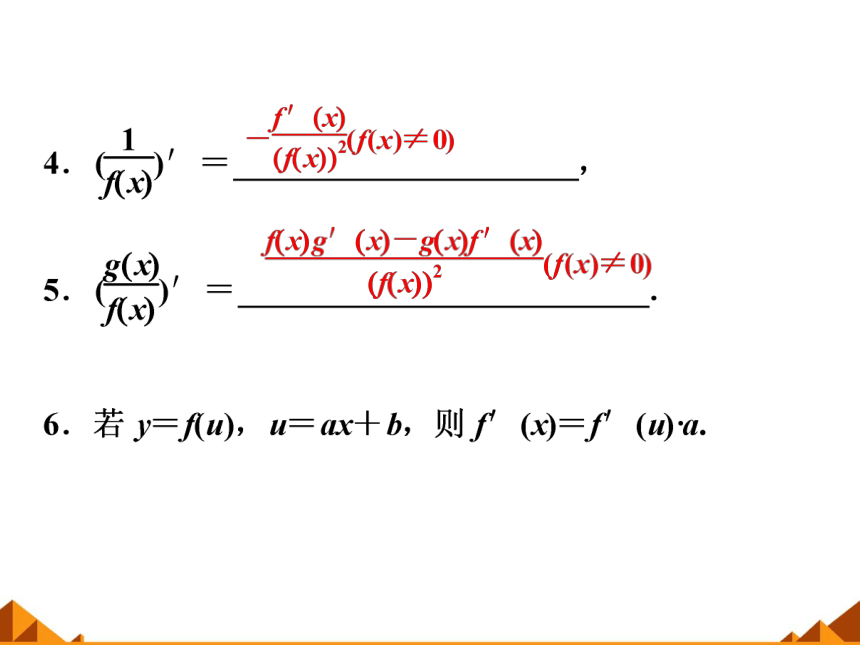




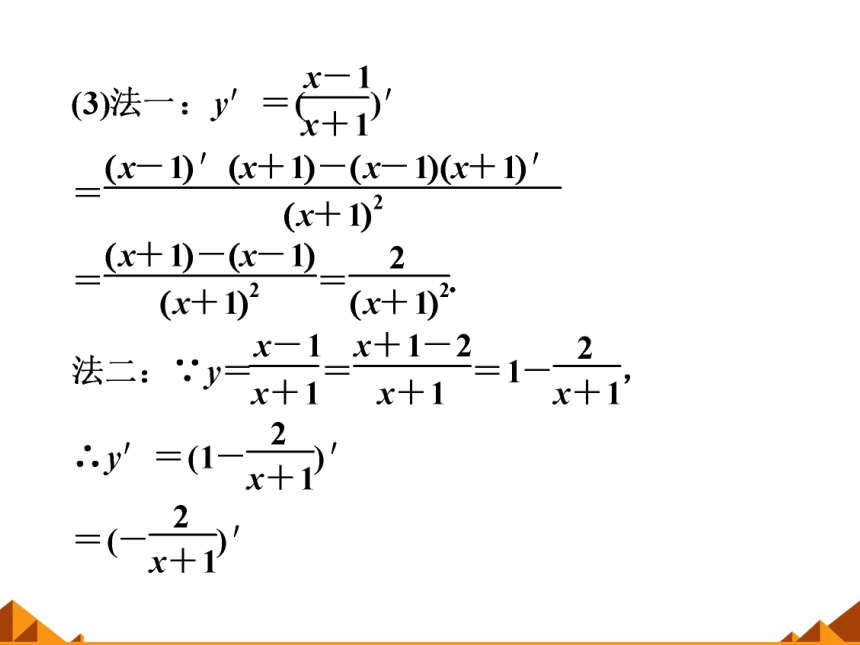
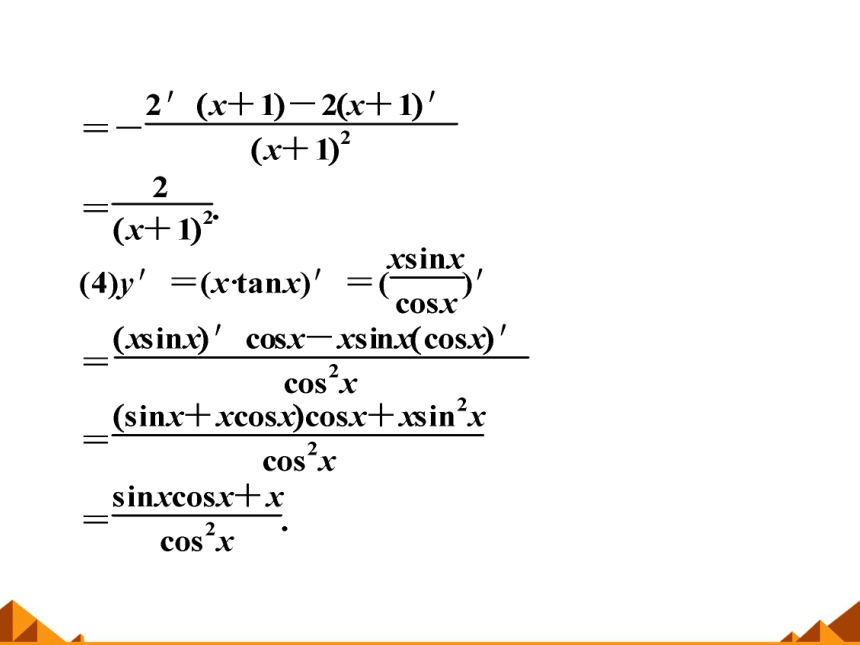

文档简介
导数的运算法则
学习目标
1.理解导数四则运算法则的推导方法.
2.掌握导数的四则运算法则.
3.会利用导数的四则运算法则进行简单导数计算.
课前自主学案
温故夯基
αxα-1
1.(xα)′=________ (α为实数),
2.(ax)′=__________ (a>0),
3.(logax)′=_________(a>0,a≠1),
4.(cosx)′=__________,
5.(tanx)′=_________,
6.(cotx)′=____________.
axlna
-sinx
知新益能
cf′(x)
导数运算法则
1.(cf(x))′=___________,
2.(f(x)+g(x))′=_________________,
(f(x)-g(x))′=________________,
3.(f(x)g(x))′=______________________,
f′(x)+g′(x)
f′(x)-g′(x)
f′(x)g(x)+f(x)g′(x)
导数的运算法则成立的条件是什么?
提示:要求两个函数必须都可导且商式中的分母不为零.
思考感悟
课堂互动讲练
求导法则的直接运用
考点突破
解决函数的求导问题,应先分析所给函数的结构特点,选择正确的公式和法则,对较为复杂的求导运算,一般综合了和、差、积、商几种运算,在求导之前应先将函数化简,然后求导,以减少运算量.
例1
【名师点评】 (1)当函数结构形式比较复杂时,要将函数式先进行化简,化成若干较简单的基本初等函数的四则运算形式,然后再利用求导法则进行运算.
(2)运用导数四则运算法则要注意的问题:
①在求导数时有些函数虽然表面形式上为函数的商或积,但在求导前利用代数或三角恒等变形可将函数先化简,然后进行求导,可避免使用积、商的求导法则,从而减少运算量,提高运算速度,避免出错.
求复合函数的导数
例2
【思路点拨】 要明确中间变量u所表示的关系.
【规律小结】 利用复合函数求导法则求复合函数的导数的步骤:
(1)分解复合函数为基本初等函数,适当选取中间变量;
(2)求每一层基本初等函数的导数;
(3)每层函数求导后,需把中间变量转化为自变量的函数.
曲线的切线方程
例3
已知抛物线y=ax2+bx+c通过点(1,1),且在点(2,-1)处与直线y=x-3相切,求a、b、c的值.
【思路点拨】 题中涉及三个未知量,已知三个独立条件,因此,要通过解方程组来确定a、b、c的值.
方法感悟
学习目标
1.理解导数四则运算法则的推导方法.
2.掌握导数的四则运算法则.
3.会利用导数的四则运算法则进行简单导数计算.
课前自主学案
温故夯基
αxα-1
1.(xα)′=________ (α为实数),
2.(ax)′=__________ (a>0),
3.(logax)′=_________(a>0,a≠1),
4.(cosx)′=__________,
5.(tanx)′=_________,
6.(cotx)′=____________.
axlna
-sinx
知新益能
cf′(x)
导数运算法则
1.(cf(x))′=___________,
2.(f(x)+g(x))′=_________________,
(f(x)-g(x))′=________________,
3.(f(x)g(x))′=______________________,
f′(x)+g′(x)
f′(x)-g′(x)
f′(x)g(x)+f(x)g′(x)
导数的运算法则成立的条件是什么?
提示:要求两个函数必须都可导且商式中的分母不为零.
思考感悟
课堂互动讲练
求导法则的直接运用
考点突破
解决函数的求导问题,应先分析所给函数的结构特点,选择正确的公式和法则,对较为复杂的求导运算,一般综合了和、差、积、商几种运算,在求导之前应先将函数化简,然后求导,以减少运算量.
例1
【名师点评】 (1)当函数结构形式比较复杂时,要将函数式先进行化简,化成若干较简单的基本初等函数的四则运算形式,然后再利用求导法则进行运算.
(2)运用导数四则运算法则要注意的问题:
①在求导数时有些函数虽然表面形式上为函数的商或积,但在求导前利用代数或三角恒等变形可将函数先化简,然后进行求导,可避免使用积、商的求导法则,从而减少运算量,提高运算速度,避免出错.
求复合函数的导数
例2
【思路点拨】 要明确中间变量u所表示的关系.
【规律小结】 利用复合函数求导法则求复合函数的导数的步骤:
(1)分解复合函数为基本初等函数,适当选取中间变量;
(2)求每一层基本初等函数的导数;
(3)每层函数求导后,需把中间变量转化为自变量的函数.
曲线的切线方程
例3
已知抛物线y=ax2+bx+c通过点(1,1),且在点(2,-1)处与直线y=x-3相切,求a、b、c的值.
【思路点拨】 题中涉及三个未知量,已知三个独立条件,因此,要通过解方程组来确定a、b、c的值.
方法感悟
同课章节目录
