3.3.2函数的极大值和极小值_课件1-湘教版数学选修1-1(31张PPT)
文档属性
| 名称 | 3.3.2函数的极大值和极小值_课件1-湘教版数学选修1-1(31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 21:37:35 | ||
图片预览











文档简介
自主探究
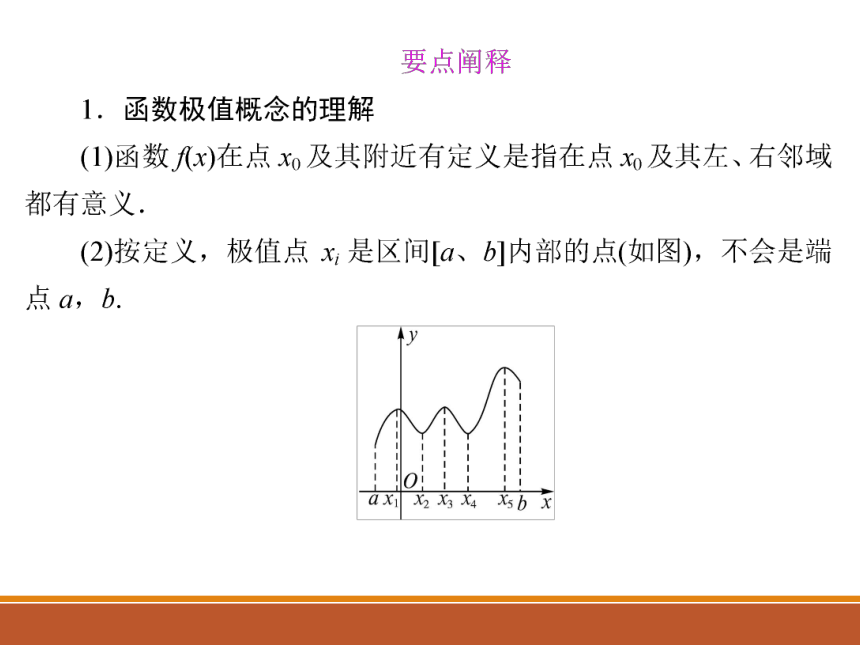
在一个给定区间上,函数的极值有怎样的情形?
提示 在一个给定的区间上,函数可能有若干个极值点,也可能不存在极值点;函数可以只有极大值,没有极小值,或者只有极小值没有极大值;也可以既有极大值,又有极小值.极大值不一定比极小值大,极小值也不一定比极大值小.
预习测评
1.关于极值,如下叙述正确的是( ).
A.若f′(x0)=0,则f(x0)是极值
B.对于函数f(x),极大值和极小值是惟一的
C.极大值总比极小值大
D.极大值可能是最大值
解析 比如y=-x2,极大值0也是最大值.
答案 D
3.函数y=x3-27x的极大值是________.
4.函数f(x)=ax3+bx在x=1处有极值-2,则a、b的值分别为________、________.
点评 (1)为了便于确定方程f′(x)=0的根是不是极值点,是极大值点还是极小值点,通常借用表格进行.
(2)可导函数y=f(x)在点x0处取得极值的充要条件是f′(x0)=0,且在x0左侧与右侧f′(x)的符号不同.
点评 正确理解函数在给定区间上有极值的实质,将函数的极值问题转化为二次方程根的分布问题,这样本题就能迎刃而解.
点评 对于可导函数,极值点导数为零,但导数为0的点不一定是极值点,因此已知函数的极值点,求某些参变量的值时,应验证能否使函数取到极值,否则易出现错解.
在一个给定区间上,函数的极值有怎样的情形?
提示 在一个给定的区间上,函数可能有若干个极值点,也可能不存在极值点;函数可以只有极大值,没有极小值,或者只有极小值没有极大值;也可以既有极大值,又有极小值.极大值不一定比极小值大,极小值也不一定比极大值小.
预习测评
1.关于极值,如下叙述正确的是( ).
A.若f′(x0)=0,则f(x0)是极值
B.对于函数f(x),极大值和极小值是惟一的
C.极大值总比极小值大
D.极大值可能是最大值
解析 比如y=-x2,极大值0也是最大值.
答案 D
3.函数y=x3-27x的极大值是________.
4.函数f(x)=ax3+bx在x=1处有极值-2,则a、b的值分别为________、________.
点评 (1)为了便于确定方程f′(x)=0的根是不是极值点,是极大值点还是极小值点,通常借用表格进行.
(2)可导函数y=f(x)在点x0处取得极值的充要条件是f′(x0)=0,且在x0左侧与右侧f′(x)的符号不同.
点评 正确理解函数在给定区间上有极值的实质,将函数的极值问题转化为二次方程根的分布问题,这样本题就能迎刃而解.
点评 对于可导函数,极值点导数为零,但导数为0的点不一定是极值点,因此已知函数的极值点,求某些参变量的值时,应验证能否使函数取到极值,否则易出现错解.
同课章节目录
