3.4生活中的优化问题举例_课件1(1)-湘教版数学选修1-1(34张PPT)
文档属性
| 名称 | 3.4生活中的优化问题举例_课件1(1)-湘教版数学选修1-1(34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 00:00:00 | ||
图片预览











文档简介
自主探究
利用导数解决实际问题中的最值问题时应注意什么?
提示 (1)在求实际问题的最大(小)值时,一定要注意考虑实际问题的意义,不符合实际意义的值应舍去.
(2)在实际问题中,有时会遇到函数在区间内只有一个点使f′(x)=0的情形,如果函数在这点有极大(小)值,那么不与端点值比较,也可以知道这就是最大(小)值.
(3)在解决实际优化问题中,不仅要注意将问题中涉及的变量关系用函数关系式给予表示,还应确定函数关系式中自变量的定义区间.
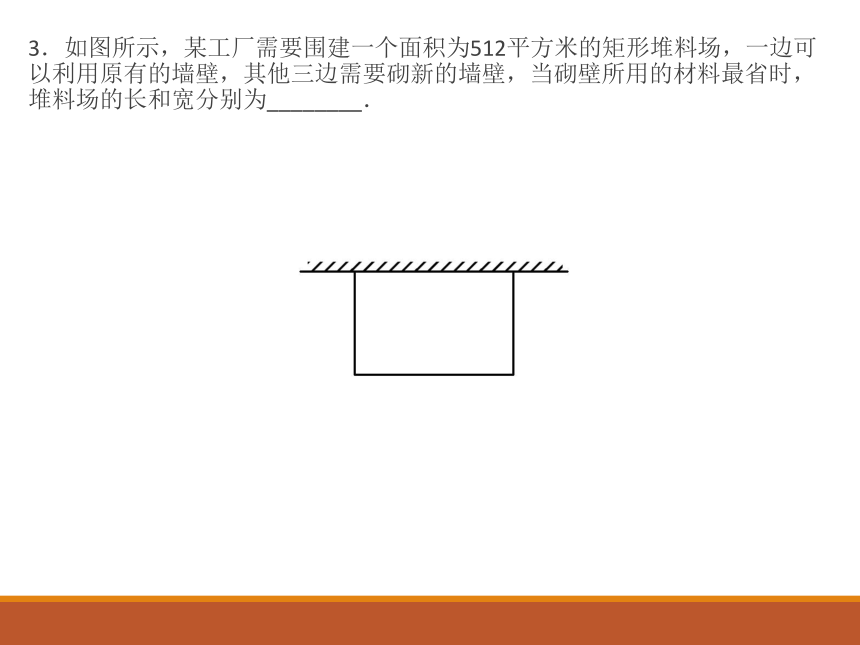
3.如图所示,某工厂需要围建一个面积为512平方米的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁,当砌壁所用的材料最省时,堆料场的长和宽分别为________.
4.用总长为6 m的钢条制作一个长方体容器的框架,如果所制作容器的底面的相邻两边长之比为3∶4,那么容器容积最大时,高为______m.
注意 (1)求实际问题的最值时,一定要考虑问题的实际意义,不符合实际意义的理论值要舍去.
(2)在实际问题中,若在函数的定义域内,使f′(x)=0成立的值只有一个,且函数在这一点处取得极大(小)值,则不与端点值比较,也可以知道这就是最大(小)值.
题型一 容积(或面积)最大问题
【例1】 在边长为60 cm的正方形铁片的四角上切去边长相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
题型二 时间、费用最省问题
【例2】 某地建一座桥,两端的桥墩已建好,这两墩相距m米,余下工程只需建两端桥墩之间的桥面和桥墩.经测算,一个桥墩的工程费用为256万元,距离为x米的相邻两墩之间的桥面工程费用为(2+)x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素.记余下工程的费用为y万元.
(1)试写出y关于x的函数关系式;
(2)当m=640米时,需新建多少个桥墩才能使y最小?
∴当x=20时y有最小值.即轮船以20 km/h的速度航行时,能使每千米的费用总和最小.
答案 20
题型三 利润最大问题
【例3】 某商品每件成本9元,售价30元,每星期卖出432件.如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值x(单位:元,0≤x≤30)的平方成正比.已知商品单价降低2元时,一星期多卖出24件.
(1)将一个星期的商品销售利润表示成x的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
利用导数解决实际问题中的最值问题时应注意什么?
提示 (1)在求实际问题的最大(小)值时,一定要注意考虑实际问题的意义,不符合实际意义的值应舍去.
(2)在实际问题中,有时会遇到函数在区间内只有一个点使f′(x)=0的情形,如果函数在这点有极大(小)值,那么不与端点值比较,也可以知道这就是最大(小)值.
(3)在解决实际优化问题中,不仅要注意将问题中涉及的变量关系用函数关系式给予表示,还应确定函数关系式中自变量的定义区间.
3.如图所示,某工厂需要围建一个面积为512平方米的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁,当砌壁所用的材料最省时,堆料场的长和宽分别为________.
4.用总长为6 m的钢条制作一个长方体容器的框架,如果所制作容器的底面的相邻两边长之比为3∶4,那么容器容积最大时,高为______m.
注意 (1)求实际问题的最值时,一定要考虑问题的实际意义,不符合实际意义的理论值要舍去.
(2)在实际问题中,若在函数的定义域内,使f′(x)=0成立的值只有一个,且函数在这一点处取得极大(小)值,则不与端点值比较,也可以知道这就是最大(小)值.
题型一 容积(或面积)最大问题
【例1】 在边长为60 cm的正方形铁片的四角上切去边长相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
题型二 时间、费用最省问题
【例2】 某地建一座桥,两端的桥墩已建好,这两墩相距m米,余下工程只需建两端桥墩之间的桥面和桥墩.经测算,一个桥墩的工程费用为256万元,距离为x米的相邻两墩之间的桥面工程费用为(2+)x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素.记余下工程的费用为y万元.
(1)试写出y关于x的函数关系式;
(2)当m=640米时,需新建多少个桥墩才能使y最小?
∴当x=20时y有最小值.即轮船以20 km/h的速度航行时,能使每千米的费用总和最小.
答案 20
题型三 利润最大问题
【例3】 某商品每件成本9元,售价30元,每星期卖出432件.如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值x(单位:元,0≤x≤30)的平方成正比.已知商品单价降低2元时,一星期多卖出24件.
(1)将一个星期的商品销售利润表示成x的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
同课章节目录
