第一章 常用逻辑用语 复习课件-湘教版数学选修1-1(23张PPT)
文档属性
| 名称 | 第一章 常用逻辑用语 复习课件-湘教版数学选修1-1(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 00:00:00 | ||
图片预览






文档简介
第一章 常用逻辑用语
复习课件
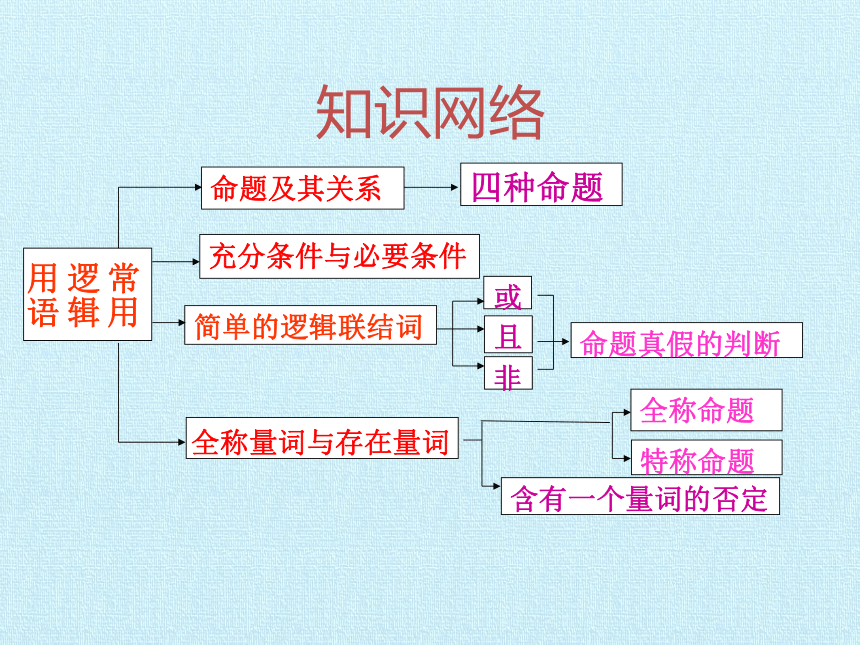
知识网络
常用逻辑用语
命题及其关系
简单的逻辑联结词
充分条件与必要条件
全称命题
特称命题
含有一个量词的否定
或
且
非
命题真假的判断
全称量词与存在量词
四种命题
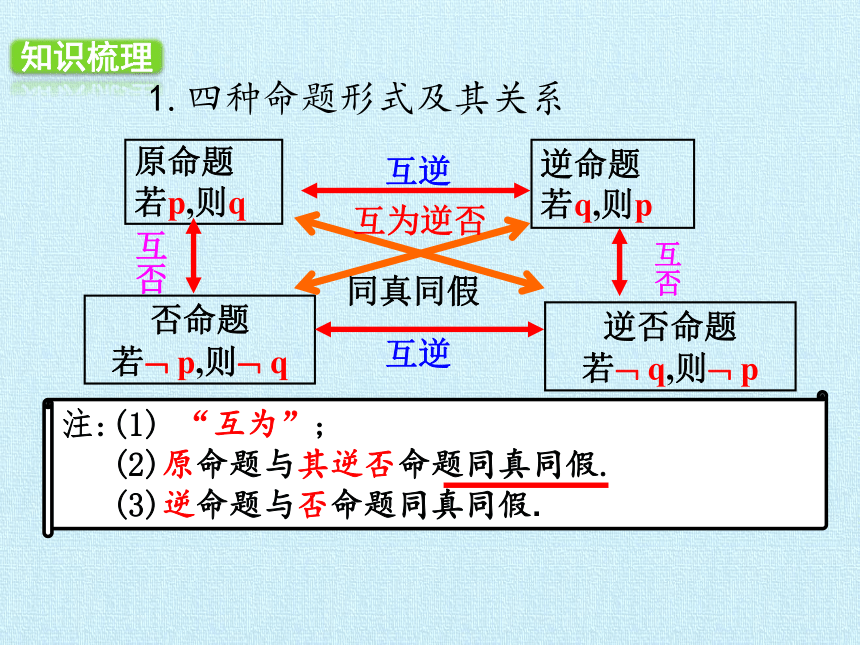
注:(1) “互为”;
(2)原命题与其逆否命题同真同假.
(3)逆命题与否命题同真同假.
原命题
若p,则q
逆否命题
若? q,则? p
否命题
若? p,则? q
逆命题
若q,则p
互逆
互否
互否
互逆
互为逆否
同真同假
知识梳理
1.四种命题形式及其关系
充分条件与必要条件的定义
从集合角度理解
若p?q,则p是q的_____条件,q是p的_____条件
p成立的对象的集合为A,q成立的对象的集合为B
p是q的_________条件
A是B的______
集合与充要条件
的关系
p是q的_________条件
B是A的______
p是q的_____条件
p?q
A___B
p是q的_________
_________条件
A,B互不____
2.充分条件与必要条件
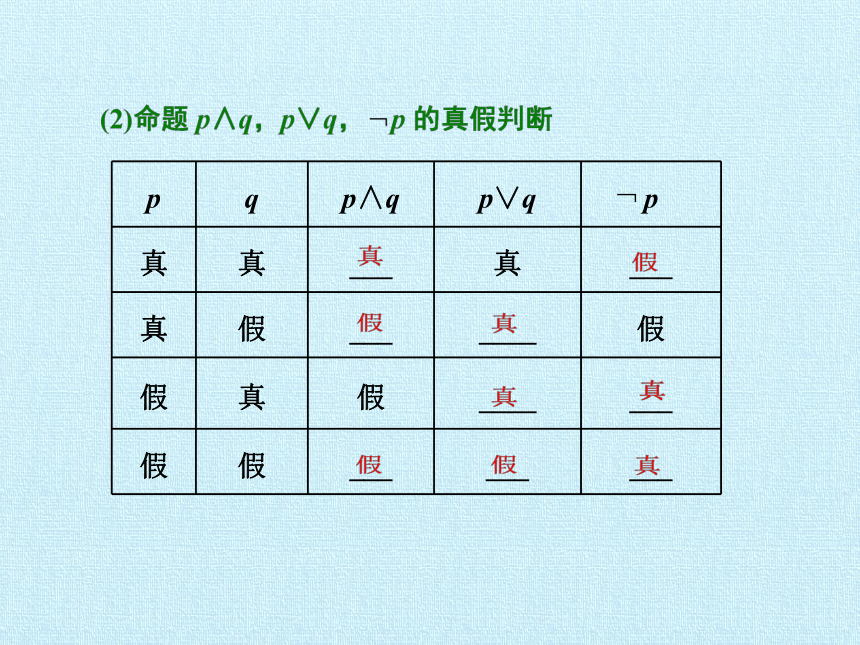
3.简单的逻辑联结词
p
q
p∧q
p∨q
p
真
真
___
真
___
真
假
___
____
假
假
真
假
____
___
假
假
___
___
___
量词名称
常见量词
符号表示
全称量词
所有、一切、任意、全部、每一个等
存在量词
存在一个、至少一个、有些、某些等
4.全称量词和存在量词
名称
形式
全称命题
特称命题
结构
对M中的任意一个x,有p(x)成立
存在M中的一个x0,使p(x0)成立
简记
否定
5.全称命题和特称命题
题型一:四种命题及其关系
典例精析
【规范解答】
直接法 间接法
原命题为真,
逆命题:若关于x的方程x2-x-k=0有实数根,则k>0.
否命题:若k≤0,则关于x的方程x2-x-k=0没有实数根.
逆否命题:若关于x的方程x2-x-k=0没有实数根,则k≤0.
假
假
假
真
题型二:充分、必要条件的判断及应用
充分不必要条件
归纳总结:准确化简条件,也就是求出每个条件对应的充要条件;注意问题的形式;可借助两个集合之间的关系来判断。
题型三:含有逻辑联结词的命题
例3.已知命题p:x2+4x+3≥0,q:x∈Z,且“p∧q”与
“ q”同时为假命题,则x=______.
【规范解答】
解析:若p为真,则x≥-1或x≤-3,
因为“
q”为假,则q为真,即x∈Z,
又因为“p∧q”为假,所以p为假,故-3<x<-1,
由题意,得x=-2.
答案:-2
归纳总结
题型四:含有一个量词的命题的否定
典例精析
例4. (1) 命题“函数y=f(x)(x∈M)是偶函数”的否定可表示为( )
A.?x0∈M,f(-x0)≠f(x0)
B.?x∈M,f(-x)≠f(x)
C.?x∈M,f(-x)=f(x)
D.?x0∈M,f(-x0)=f(x0)
(2)若命题“?x0∈R,使得x02+(a-1)x0+1<0”是真命题,则实数a的取值范围是________.
【规范解答】(1)选A 命题“函数y=f(x)(x∈M)是偶函数”即“?x∈M,f(-x)=f(x)”,该命题是一个全称命题,其否定是一个特称命题,即“?x0∈M,f(-x0)≠f(x0)”
归纳总结
课堂小结
本章的知识网络
四部分知识内容
四大常见题型
练一练
【解析】
2.在△ABC中,角A,B,C所对应的边分别为a,b,c,则“a≤b”是“sin A≤sin B”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
3.已知集合A={x||x|≤4,x∈R},B={x|x<a},则“a>5”是“A?B”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【解析】 (1)由正弦定理,知a≤b?2Rsin A≤2Rsin B(R为△ABC外接圆的半径)?sin A≤sinB.故选A.
(2)A={x||x|≤4,x∈R}?A={x|-4≤x≤4},所以A?B?a>4,而a>5?a>4,且a>4?a>5,所以“a>5”是“A?B”的充分不必要条件.
3.已知命题p:函数f(x)=x2+mx+1的图象与x轴负半轴有两个不同的交点;命题q:方程4x2+4(m-2)x+1=0无实根.若“p或q”为真,“p且q”为假,求实数m的取值范围.
【解析】因为命题p:函数f(x)=x2+mx+1的图象与x轴负半轴有两个不同的交点,所以
∴m>2.因为命题q:方程4x2+4(m-2)x+1=0无实根,所以q:Δ=16(m-2)2-16=16(m2-4m+3)<0, ∴1∵p或q为真,p且q为假,∴p真q假或p假q真.
【解析】
谢 谢
复习课件
知识网络
常用逻辑用语
命题及其关系
简单的逻辑联结词
充分条件与必要条件
全称命题
特称命题
含有一个量词的否定
或
且
非
命题真假的判断
全称量词与存在量词
四种命题
注:(1) “互为”;
(2)原命题与其逆否命题同真同假.
(3)逆命题与否命题同真同假.
原命题
若p,则q
逆否命题
若? q,则? p
否命题
若? p,则? q
逆命题
若q,则p
互逆
互否
互否
互逆
互为逆否
同真同假
知识梳理
1.四种命题形式及其关系
充分条件与必要条件的定义
从集合角度理解
若p?q,则p是q的_____条件,q是p的_____条件
p成立的对象的集合为A,q成立的对象的集合为B
p是q的_________条件
A是B的______
集合与充要条件
的关系
p是q的_________条件
B是A的______
p是q的_____条件
p?q
A___B
p是q的_________
_________条件
A,B互不____
2.充分条件与必要条件
3.简单的逻辑联结词
p
q
p∧q
p∨q
p
真
真
___
真
___
真
假
___
____
假
假
真
假
____
___
假
假
___
___
___
量词名称
常见量词
符号表示
全称量词
所有、一切、任意、全部、每一个等
存在量词
存在一个、至少一个、有些、某些等
4.全称量词和存在量词
名称
形式
全称命题
特称命题
结构
对M中的任意一个x,有p(x)成立
存在M中的一个x0,使p(x0)成立
简记
否定
5.全称命题和特称命题
题型一:四种命题及其关系
典例精析
【规范解答】
直接法 间接法
原命题为真,
逆命题:若关于x的方程x2-x-k=0有实数根,则k>0.
否命题:若k≤0,则关于x的方程x2-x-k=0没有实数根.
逆否命题:若关于x的方程x2-x-k=0没有实数根,则k≤0.
假
假
假
真
题型二:充分、必要条件的判断及应用
充分不必要条件
归纳总结:准确化简条件,也就是求出每个条件对应的充要条件;注意问题的形式;可借助两个集合之间的关系来判断。
题型三:含有逻辑联结词的命题
例3.已知命题p:x2+4x+3≥0,q:x∈Z,且“p∧q”与
“ q”同时为假命题,则x=______.
【规范解答】
解析:若p为真,则x≥-1或x≤-3,
因为“
q”为假,则q为真,即x∈Z,
又因为“p∧q”为假,所以p为假,故-3<x<-1,
由题意,得x=-2.
答案:-2
归纳总结
题型四:含有一个量词的命题的否定
典例精析
例4. (1) 命题“函数y=f(x)(x∈M)是偶函数”的否定可表示为( )
A.?x0∈M,f(-x0)≠f(x0)
B.?x∈M,f(-x)≠f(x)
C.?x∈M,f(-x)=f(x)
D.?x0∈M,f(-x0)=f(x0)
(2)若命题“?x0∈R,使得x02+(a-1)x0+1<0”是真命题,则实数a的取值范围是________.
【规范解答】(1)选A 命题“函数y=f(x)(x∈M)是偶函数”即“?x∈M,f(-x)=f(x)”,该命题是一个全称命题,其否定是一个特称命题,即“?x0∈M,f(-x0)≠f(x0)”
归纳总结
课堂小结
本章的知识网络
四部分知识内容
四大常见题型
练一练
【解析】
2.在△ABC中,角A,B,C所对应的边分别为a,b,c,则“a≤b”是“sin A≤sin B”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
3.已知集合A={x||x|≤4,x∈R},B={x|x<a},则“a>5”是“A?B”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【解析】 (1)由正弦定理,知a≤b?2Rsin A≤2Rsin B(R为△ABC外接圆的半径)?sin A≤sinB.故选A.
(2)A={x||x|≤4,x∈R}?A={x|-4≤x≤4},所以A?B?a>4,而a>5?a>4,且a>4?a>5,所以“a>5”是“A?B”的充分不必要条件.
3.已知命题p:函数f(x)=x2+mx+1的图象与x轴负半轴有两个不同的交点;命题q:方程4x2+4(m-2)x+1=0无实根.若“p或q”为真,“p且q”为假,求实数m的取值范围.
【解析】因为命题p:函数f(x)=x2+mx+1的图象与x轴负半轴有两个不同的交点,所以
∴m>2.因为命题q:方程4x2+4(m-2)x+1=0无实根,所以q:Δ=16(m-2)2-16=16(m2-4m+3)<0, ∴1
【解析】
谢 谢
同课章节目录
